پیاده سازی جدول هش (Hash Table) در جاوا اسکریپت – راهنمای مقدماتی

ساختار {} در جاوا اسکریپت بسیار کارآمد است، زیرا امکان ذخیره‌سازی و بازیابی مقادیر بر اساس کلیدهایشان را به روشی کم‌هزینه یعنی (O(1 فراهم می‌سازد. در این نوشته تلاش می‌کنیم که جدول هش را پیاده‌سازی کنیم و همچنین نگاهی به ساز و کار درونی جدول هش به عنوان یکی از نبوغ‌آمیزترین ایده‌های مطرح شده در علوم رایانه بپردازیم.

بیان مسئله

فرض کنید در حال ساخت یک زبان برنامه‌نویسی جدید هستید. ابتدا از انواع داده کاملاً ساده مانند رشته‌ها، اعداد صحیح، اعشاری و غیره شروع می‌کنید و سپس ساختمان‌های داده بسیار ابتدایی را پیاده‌سازی می‌کنید. ابتدا با آرایه ([]) مواجه می‌شوید و سپس جدول هش را می‌بینید. جدول هش را به صورت دیکشنری (dictionary)، آرایه انجمنی (associative array)، نگاشت هش (hashmap)، نگاشت (map) و اسامی دیگری نیز می‌شناسند. در ادامه در مورد طرز کار جدول هش و دلیل سریع بودن آن توضیح می‌دهیم.

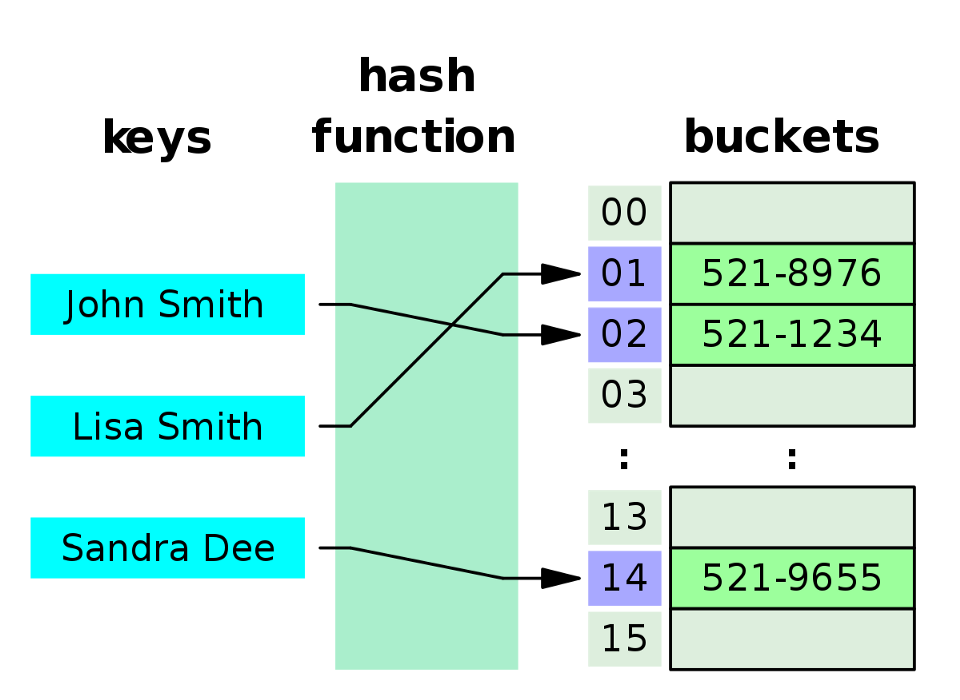
اگر کنجکاو شده‌اید که چرا این ساختمان داده جدول هش نامیده می‌شود، باید بگوییم که دلیل آن، این است که یک تابع هش (درهم سازی) روی کلیدهایی که درج یا بازیابی می‌شوند اجرا می‌شود. از این تابع برای تبدیل کلید به عدد صحیح i استفاده می‌کنیم و سپس مقدار به دست آمده را در اندیس i لیست درونی خود ذخیره می‌کنیم. از آنجا که ما بر اساس اندیس به عناصر مختلف دسترسی می‌یابیم، این کار هزینه ثابتی به صورت (O(1 خواهد داشت و از این رو پیچیدگی جدول هش نیز برابر با (O(1 خواهد بود.

let hash = require('string-hash')

class DumbMap {
  constructor() {
    this.list = []
  }

  get(x) {
    return this.list[hash(x)]
  }

  set(x, y) {
    this.list[hash(x)] = y
  }
}

ما در کد فوق از ماژول string-hash استفاده می‌کنیم که کار آن صرفاً تبدیل یک رشته به هش عددی است. از آن برای ذخیره‌سازی و واکشی عناصر در اندیس (hash(key لیست خود استفاده می‌کنیم. نتیجه به صورت زیر است:

with lots of records in the map: 0.013ms

می‌بینید که سرعت اجرا تا چه حد افزایش یافته است. دیگر لازم نیست حلقه‌ای روی همه عناصر اجرا کنیم و بدین ترتیب بازیابی عناصر از DumbMap بسیار سریع خواهد بود.

به بیان کاملاً سرراست: «هش کردن همان کاری است که باعث می‌شود جدول‌های هش بسیار کارآمد باشند»

هزینه انتخاب تابع هش کردن مناسب

البته انتخاب یک تابع هش کردن مناسب بسیار مهم است. اگر (hash(key زمان اجرایی چندثانیه‌ای داشته باشد، تابع ما صرف نظر از پیچیدگی‌اش کاملاً کُند خواهد بود. همچنین کاملاً مهم است که تابع هش کردن تصادم‌های زیادی ایجاد نکند. چون تصادم هش باعث افزایش پیچیدگی جدول هش می‌شود. در ادامه در مورد تصادم هش بیشتر توضیح داده‌ایم.

تصادم‌ها

ممکن است با خود فکر کنید که یک تابع هش، هرگز موارد تصادم ایجاد نمی‌کند. اما در دنیای واقعی همه چیز متفاوت است. گوگل موفق شده موارد تصادم را برای الگوریتم هش کردن SHA-1 ایجاد کند، که گزارش آن را می‌توانید در این لینک (+) بخوانید. تصادمبسته به توان محاسباتی دیر یا زود رخ خواهد داد و تابع هش کردن شکسته می‌شود و هش یکسانی برای 2 ورودی مختلف ایجاد می‌کند. همواره باید تصور کنید که تابع هش موارد تصادم را ایجاد می‌کند و از این رو رویه دفاعی مناسبی برای این وضعیت تدارک دیده باشید.

برای بررسی بیشتر یک تابع هش را استفاده می‌کنیم که موارد تصادم زیادی تولید می‌کند:

function divide(int) {
  int = Math.round(int / 2)

  if (int > 10) {
    return divide(int)
  }

  return int
}

function hash(key) {
  let h = require('string-hash')(key)
  return divide(h)
}

تابع فوق از یک آرایه 10 عنصری برای ذخیره‌سازی مقادیر استفاده می‌کند و این بدان معنی است که عناصر می‌توانند جابجا شوند و این همان باگی است که در ساختمان داده DumbMap ما نیز وجود داشت:

let m = new DumbMap()

for (x = 0; x < 1000000; x++) {
  m.set(`element${x}`, x)
}

console.log(m.get('element0')) // 999988
console.log(m.get('element1')) // 999988
console.log(m.get('element1000')) // 999987

برای حل این مشکل، می‌توان جفت‌های چندگانه کلید-مقدار را در اندیس یکسان نگه‌داری کرد. بدین ترتیب جدول هش ما به صورت زیر اصلاح می‌شود:

class DumbMap {
  constructor() {
    this.list = []
  }

  get(x) {
    let i = hash(x)

    if (!this.list[i]) {
      return undefined
    }

    let result

    this.list[i].forEach(pairs => {
      if (pairs[0] === x) {
        result = pairs[1]
      }
    })

    return result
  }

  set(x, y) {
    let i = hash(x)

    if (!this.list[i]) {
      this.list[i] = []
    }

    this.list[i].push([x, y])
  }
}

همان طور که احتمالاً متوجه شده‌اید در این حالت ما به پیاده‌سازی اولیه خود بازگشته‌ایم و لیستی از جفت‌های کلید-مقدار را ذخیره کرده و روی همه آن‌ها می‌چرخیم. این وضعیت در مواردی که تصادم‌های زیادی برای اندیس خاص لیست وجود داشته باشند، بسیار کُند خواهد بود.

بنچمارک کد فوق با استفاده از تابع ()hash که اندیس‌هایی از 1 تا 10 ایجاد می‌کند، به صورت زیر خواهد بود:

with lots of records in the map: 11.919ms

و با استفاده از تابع هش string-hash که اندیس‌های تصادفی ایجاد می‌کند، وضعیت بنچمارک چنین خواهد بود:

with lots of records in the map: 0.014ms

همان طور که می‌بینید انتخاب تابع هش کردن صحیح تا چه حد مهم است و بدین ترتیب تابع هش آن قدر سریع می‌شود که تقریباً تأثیر سوئی روی پیچیدگی تابع ما ندارد و همچنین تصادم‌های زیادی نیز تولید نمی‌کند.

آیا پیچیدگی جدول هش واقعاً (O(1 است؟

قبلاً اشاره کردیم که پیچیدگی جدول هش برابر با (O(1 است؛ اما در برخی موارد نیز چنین نیست. پیچیدگی جدول هش به تابع درهم سازی (هش کردن) که انتخاب می‌شود بستگی دارد. هر چه این تابع تصادم‌های بیشتری تولید کند، پیچیدگی جدول هش به (O(n نزدیک‌تر می‌شود.

تابع هش مانند زیر بدان معنی است که جدول هش ما پیچیدگی برابر با (O(n دارد:

function hash(key) {
return 0
}

به همین دلیل است که پیچیدگی محاسباتی به طور کلی سه معیار به صورت بهترین، میانگین و بدترین سناریو دارد. جدول‌های هش در سناریوهای بهترین حالت و حالت میانگین پیچیدگی برابر با (O(1 دارند؛ اما در سناریو بدترین حالت در دسته (O(n قرار می‌گیرند. به خاطر داشته باشید که یک تابع هش کردن خوب کلید اصلی طراحی جدول هش کارآمد است.

توضیحاتی در مورد تصادم

تکنیکی که برای اصلاح DumbMap در حالت بروز تصادم استفاده کردیم به نام زنجیره‌سازی مجزا (separate chaining) نامیده می‌شود. در این روش همه جفت‌های کلید-مقدار که تصادم تولید می‌کنند در یک لیست ذخیره شده و روی آن‌ها حلقه‌ای اجرا می‌شود.

تکنیک رایج دیگر به صورت آدرس‌دهی باز (open addressing) است. روش کار این تکنیک به صورت زیر است:

• در هر یک از اندیس‌های لیست، تنها یک جفت کلید-مقدار ذخیره می‌شود.
• زمانی که تلاش می‌کنیم یک جفت را در اندیس x ذخیره کنیم، اگر از قبل جفت کلید-مقداری در آن وجود داشته باشد، جفت جدید را در اندیس x+1 ذخیره می‌کنیم.
• اگر x+1 نیز اشغال شده باشد،x+2 و همین طور تا اولین اندیس غیر اشغال را بررسی می‌کنیم.
• زمانی که یک عنصر را بازیابی می‌کنیم، کلید را هش می‌کنیم و بررسی می‌کنیم که آیا آن عنصر در موقعیت x با کلید ما مطابقت دارد یا نه.
• اگر چنین نباشد به عنصر در موقعیت x+1 دسترسی می‌یابیم.
• این فرایند را تا زمانی که به انتهای لیست برسیم یا هنگامی که یک اندیس خالی بیابیم، تکرار می‌کنیم. این بدان معنی است که عنصر ما در جدول هش وجود ندارد.

این روشی ساده، هوشمندانه، عالی و در اغلب موارد کاملاً کارآمد است.

سؤالاتی در مورد جدول هش

در این بخش برخی از سؤال‌هایی که معمولاً در مورد جدول هش پرسیده می‌شوند و پاسخ آن‌ها را ارائه کرده‌ایم:

آیا در جدول هش مقادیری که ذخیره می‌شوند، نیز هش می‌شوند؟

نه، مقادیر هش نمی‌شوند و صرفاً کلیدها هش می‌شوند. بدین ترتیب می‌توان آن‌ها را به یک عدد صحیح i تبدیل کرد و هر دو متغیر کلید و مقدار در موقعیت i یک لیست ذخیره می‌شوند.

آیا تابع‌های هش کردن که از سوی جدول‌های هش استفاده می‌شوند، تصادم هش ایجاد می‌کنند؟

بله حتماً چنین است و از این رو جدول‌های هش به همراه راهبردهای دفاعی برای جلوگیری از بروز باگ پیاده‌سازی می‌شوند.

جدول هش به صورت درونی از یک لیست استفاده می‌کند یا از لیست پیوندی؟

این مسئله بستگی به نوع جدول هش دارد و در موقعیت‌های مختلف از هر کدام از آن‌ها استفاده می‌شود. ما در مثال‌های این مقاله از آرایه جاوا اسکریپت ([]) استفاده کرده‌ایم که می‌توان اندازه آن را به صورت دینامیک تغییر داد:

> a = []
> a[3] = 1
> a
[<3 empty items>, 1]

چرا در این مثال‌ها از جاوا اسکریپت استفاده شده، در حالی که آرایه‌های جاوا اسکریپت خودشان نوعی جدول هش هستند؟

برای نمونه:

> a = []
[]
> a["some"] = "thing"
'thing'
> a
[some: 'thing']
> typeof a
'object'

ما بر این نکته واقف هستیم؛ اما جاوا اسکریپت زبانی کاملاً جهانی محسوب می‌شود و هنگام بررسی مثال‌ها، زبان ساده‌ای برای مفهوم آن‌ها محسوب می‌شود. جاوا اسکریپت شاید بهترین زبان برنامه‌نویسی نباشد؛ اما امیدواریم مثال‌های ارائه شده در این مقاله به اندازه کافی روشن باشند.

آیا مثال‌های این نوشته واقعاً پیاده‌سازی‌های مناسبی از یک جدول هش هستند؟ آیا جدول هش واقعاً به همین سادگی است؟

نه اصلاً چنین نیست. موارد زیاد دیگری نیز هستند که باید بیاموزید.

سخن پایانی

جدول‌های هش ایده بسیار هوشمندانه‌ای هستند که در موارد مختلف مورد استفاده قرار می‌گیرند.

فیلم مجموعه آموزش جاوا اسکریپت JavaScript – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

مهم نیست که در حال ساخت یک دیکشنری در پایتون باشیم یا از آرایه‌های انجمنی در PHP استفاده می‌کنیم و یا ساختار Map را در جاوا اسکریپت مورد استفاده قرار دهیم؛ چون در هر حال مشغول استفاده از جدول هش هستیم. همه این ساختمان‌های داده، مفاهیم مشترکی دارند و به روشی مؤثری امکان بازیابی عناصر با استفاده از یک شناسه را با پیچیدگی تقریباً ثابتی ارائه می‌کنند. امیدواریم از این نوشته لذت برده باشید. شما می‌توانید دیدگاه‌ها و پیشنهادهای خود را در بخش نظرات این نوشته با ما و دیگر خوانندگان فرادرس در میان بگذارید.

اگر این مطلب برایتان مفیده بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های علوم کامپیوتر
• درهم‌سازی (Hashing) در عصر یادگیری ماشین — معرفی جدیدترین تحولات این رشته
• مجموعه آموزش‌های برنامه‌نویسی
• آموزش مروری بر توابع Hash و خطر تصادم در آن ها
• انواع الگوریتم های جستجو و Hash Table — راهنمای جامع
• تابع هش یا درهم سازی (Hash Function) چیست؟ — به زبان ساده

^^