الگوریتم مبتنی بر Heap با سوئیفت – از صفر تا صد
در یکی از مطالب قبلی مجله فرادرس به بررسی الگوریتم «دایجسترا» (Dijkstra) برای جستجوی یک گراف پرداختیم. این الگوریتم که در سال 1959 انتشار یافته است، یک تکنیک رایج برای یافتن کوتاهترین مسیر در مسائل پیچیده محسوب میشود. در آن مقاله به بررسی جنبههای گوناگون از قبیل پیمایش گراف، ساختمانهای داده سفارشی و «رویکرد حریصانه» (greedy approach) پرداختیم. زمانی که برنامهها را طراحی میکنیم، تماشای کار کردن آنها حس خوبی ایجاد میکند. استفاده از الگوریتم دایجسترا به ما امکان میدهد که کوتاهترین مسیر بین رأس مبدأ و مقصد را بیابیم. با این حال این رویکرد را میتوان بهبود بخشید تا کارآمدتر شود. در این مقاله قصد داریم با استفاده از الگوریتم مبتنی بر Heap این بهینهسازی را اجرا کنیم. برای مطالعه مقاله قبلی میتوانید روی لینک زیر کلیک کنید:

الگوریتم کوتاهترین مسیر دایجسترا در سوئیفت — به زبان ساده
طرز کار الگوریتم مبتنی بر Heap
ساحتمان داده Heap اساساً فقط از یک آرایه تشکیل یافته است.
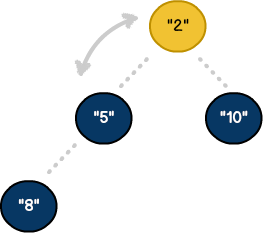
با این حال برخلاف آرایه آن را به صورت درخت بصریسازی میکنیم. کلمه «بصریسازی» بدین معنی است که از تکنیکهای پردازشی استفاده میکنیم که به طور معمول با ساختمانهای داده بازگشتی مرتبط هستند. این تغییر در طرز تفکر، مزیتهای زیادی دارد. به مثال زیر توجه کنید:
چنان که میبینید، numberList را میتوان به سادگی به صورت یک Heap تصور کرد. با آغاز از اندیس 0، آیتمها یک نقطه متناظر را به صورت گره والد یا فرزند پر میکنند. هر والد نیز به استثنای اندیس شماره 2 دارای دو فرزند است.
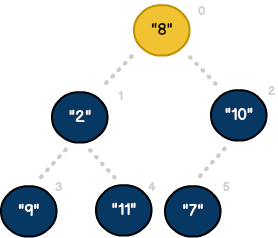
از آنجا که چیدمان مقادیر ترتیبی است، یک الگوی ساده ظاهر میشود. در هر گره میتوانیم موقعیت را به دقت به وسیله استفاده از فرمولهای زیر پیشبینی کنیم:
هیپهای مرتبسازی
یکی از ویژگیهای جالب هیپ، توانایی آن برای مرتبسازی است.
الگوریتمهای زیادی برای مرتبسازی دنبالههای دادهها طراحی شدهاند و هنگامی که به مرتبسازی هیپها میپردازیم، گرهها میتوانند طوری چیدمان یابند که هر والد مقداری کمتر از فرزندانش باشد. در علوم رایانه این کار به نام «هیپ-کمینه» (min-heap) خوانده میشود:
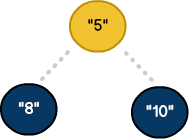
در الگوریتم دایجسترا از مفهومی به نام frontier استفاده کردیم. Frontier به صورت یک آرایه ساده کدنویسی شده که در آن وزن کلی هر مسیر را برای یافتن کوتاهترین مسیر مورد مقایسه قرار دادیم:
با این که این روش پاسخگو بود، اما در واقع ما از تکنیک brute force استفاده کردیم. به بیان دیگر ما همه مسیرهای بالقوه را برای یافتن کوتاهترین مسیر مورد بررسی قرار دادهایم. این قطعه کد در یک زمان خطی O(n) اجرا میشود. اگر frontier شامل یک میلیون ردیف باشد، تأثیر آن بر عملکرد کلی الگوریتم چگونه خواهد بود؟
ساختار هیپ
در این بخش یک frontier کارآمدتر میسازیم. نام این ساختمان داده جدید که کارکرد یک آرایه را بسط میدهد PathHeap میگذاریم:
کلاس PathHeap شامل دو مشخصه است. هیپ برای پشتیبانی از طراحی خوب، یک مشخصه خصوصی اعلان کرده است. count برای ردگیری تعداد آیتمها، به صورت یک «مشخصه محاسبهشده» (computed property) اعلان یافته است.
ساخت صف
برای جستجوی frontier به روشی کارآمدتر از O(n) باید طرز فکر جدیدی پیش بگیریم. میتوانیم با استفاده از هیپ، عملکردمان را تا حد O(1) بهبود بخشیم. بدین ترتیب با بهرهگیری از فرمولهای heapsort، رویکرد جدید به این صورت است که مقادیر اندیس را طوری بچینیم که کوچکترین آیتم در ریشه قرار گیرد:
متد enqueuer یک مسیر منفرد را به عنوان پارامتر میپذیرد. برخلاف دیگر الگوریتمهای مرتبسازی، هدف ما این نیست که همه آیتمها مرتبسازی شوند، بلکه میخواهیم کمترین مقدار را پیدا کنیم. این بدان معنی است که میتوانیم با مقایسه مقادیر زیرمجموعه، کارایی را بهبود ببخشیم.
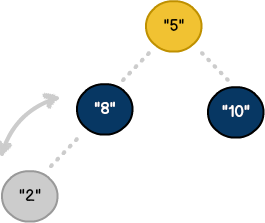
از آنجا که متد enqueuer مشخصه min-heap را نگهداری میکند، وظیفه اضافی یافتن کوتاهترین مسیر را حذف میکنیم. در نتیجه، کارایی الگوریتم تا حد زمان ثابت O(1) افزایش مییابد. در اینجا یک متد ابتدایی peek برای بازیابی آیتم در سطح ریشه پیادهسازی میکنیم:
هیپ و ژنریک
استفاده از هیپ میتواند به بهبود پیچیدگی زمانی راهحلهای مختلف کمک کند. برای این که مدل خود را برای کاربردهای عمومی بسط دهیم، میتوانیم الگوریتم تعمیمیافتهتری نیز ایجاد کنیم:
بدین ترتیب به پایان این مقاله میرسیم.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای برنامهنویسی
- آموزش برنامه نویسی Swift (سوئیفت) برای برنامه نویسی iOS
- مجموعه آموزشهای دروس علوم و مهندسی کامپیوتر
- آموزش سوئیفت (Swift) — مجموعه مقالات مجله فرادرس
- عملگرهای سفارشی در سوئیفت — از صفر تا صد
==












