جدول فراوانی برای دادههای کیفی و کمی – مثالهای کاربردی
هرچند معیارهای مرکزی و پراکندگی میتوانند خصوصیات جامعه آماری را نشان دهند ولی استفاده از جدول فراوانی نیز کمک بسیاری به شناخت جامعه آماری میکند، به خصوص در زمانی که دادهها کیفی هستند. شاید بتوان جدول فراوانی را به نوعی نشاندهنده پراکندگی برای دادهها نیز در نظر گرفت. از جدول فراوانی حتی برای استخراج خصوصیات متغیرهای کمی و کیفی مانند میانگین، میانه و نما میتوان استفاده کرد. بنابراین اگر مقدارهای یک متغیر کیفی یا کمی (که به صورت طبقهای درآمده)، موجود باشد، سعی داریم، با استفاده از جدول فراوانی پاسخ بعضی از پرسشها را پیدا کنیم. در این مطلب از مجله فرادرس در مورد جدول فراوانی برای دادههای کیفی و کمی صحبت میکنیم.


خصوصیات جدول فراوانی
جدول فراوانی از چند سطر و ستون تشکیل شده است. هر سطر نشانگر خصوصیات یک طبقه یا رده است. همچنین ویژگیهای مربوط به هر سطر نیز در ستونها نامگذاری شدهاند.
در زیر نمونه یک جدول فراوانی مشاهده میشود.
| نام رده یا حدود رده (طبقات) | فراوانی- f | فراوانی نسبی- r | فراوانی تجمعی- F | فراوانی نسبی-تجمعی- R |
| جمع |
نکته: ممکن است ستونی به عنوان شماره ردیف نیز در اول جدول قرار داشته باشد. این ستون به ارجاع آسان به سطرهای جدول فراوانی کمک میکند. مثلا اگر گفته شود که نما در رده سوم جدول فراوانی قرار دارد، به این معنی است که باید در سطر سوم به دنبال آن بگردیم. ستونهای این جدول به ترتیب از راست به چپ در ادامه معرفی میشوند.
نام رده یا حدود رده (طبقات)
براساس مقدارهای متغیر کیفی یا حدود طبقاتی که متغیر کمی دارد، مقدارهای ستون نام رده یا حدود رده ساخته میشود. برای مثال اگر گروه خون را در نظر بگیریم، نام رده برای هر سطر، یکی از گروههای خونی مثل A, AB, B یا O است. یا اگر مدرک تحصیلی باید در جدول فراوانی گنجانده شود، ستون نام رده میتواند اسامی مدرکهای تحصیلی باشد. مثل جدول زیر
| نام مدرک تحصیلی | زیر دیپلم | دیپلم | کاردانی | کارشناسی | کارشناسی ارشد | دکتری | پسا دکتری |
نکته: گاهی به جای ذکر مقدار متنی برای متغیرهای کیفی از کدگذاری عددی استفاده میشود. این کدها به جای نام رده نیز میتوانند در هر سطر به کار روند.
ولی اگر جدول فراوانی مربوط به متغیر کمی است، رده یا طبقاتی که براساس مقدارهای این متغیر ساخته شده، در این ستون قرار میگیرند. برای مثال ردهها، میتوانند برای حدود سنی، به صورت جدول زیر باشد:
| حدود سنی | 0-1 | 2-3 | 5-10 | 11-15 | 16-30 | 31-55 | 56-75 | 76 به بالا |
فراوانی
به تعداد تکرارهای هر مقدار از ستون رده یا حدود رده، «فراوانی» (Frequency) میگویند. این مقدار در ستون فراوانی قرار میگیرد. باید در حالتی که حدود رده وجود دارد دقت کرد که یک مشاهده در دو رده شمارش نشود. به این ترتیب مجموع ستون فراوانی برای همه ردهها برابر با تعداد نمونه یا مشاهدات (n) خواهد بود. فراوانی مربوط به رده ام را با نشان میدهیم.

فراوانی نسبی
اگر فراوانی هر رده را به جمع فراوانیها تقسیم کنیم، «فراوانی نسبی» (Relative Frequency) حاصل میشود. البته میتوان مقدار این ستون را به صورت درصدی نیز نمایش داد. برای این کار کافی است حاصل تقسیم را در ۱۰۰ ضرب کنیم و حاصل را با علامت ٪ نشان دهیم. نماد مربوط به فراوانی نسبی رده ام، به صورت است.
اگر تعداد کل فراوانیها در جدول فراوانی را با n نشان دهیم، برای نمایش شیوه محاسبه فراوانی نسبی میتوان از رابطه ریاضی زیر کمک گرفت:
در نتیجه با ضرب طرفین این تساوی، میتوان مقدار فراوانی را بر اساس فراوانی نسبی نیز محاسبه کرد.
جمع ستون فراوانی نسبی برابر با ۱ و در حالتی که مقدارهای آن به صورت درصدی باشند برابر با ۱۰۰٪ خواهد بود.
فراوانی تجمعی
برای محاسبه «فراوانی تجمعی» (Cumulative Frequency) برای هر رده، کافی است فراوانی آن رده را با فراوانی ردههای قبلی جمع کرد. فراوانی تجمعی رده iام را با نشان میدهیم. برای مثال اگر برای رده سوم به دنبال فراوانی تجمعی هستیم، کافی است فراوانی رده سوم را با فراوانی رده دوم و اول جمع کنیم.
برای محاسبه فراوانی تجمعی رده iام میتوان رابطه زیر را به بیان ریاضی نوشت:
به منظور افزایش سرعت در انجام محاسبه فراوانی تجمعی برای یک رده، کافی است فراوانی تجمعی رده قبلی را با فراوانی رده مورد نظر جمع کرد. مثلا برای محاسبه فراوانی تجمعی رده سوم کافی است فراوانی تجمعی رده دوم را با مقدار فراوانی رده سوم جمع کنیم. از آنجایی که مجموع فراوانیها تا رده دوم در ستون فراوانی تجمعی رده دوم قرار دارد، کافی است آن را با فراوانی رده سوم جمع کنیم تا فراوانی تجمعی رده سوم بدست آید.
پس میتوان فرمول زیر را برای آن نوشت:
در نتیجه رابطه زیر بین فراوانی و فراوانی تجمعی هر رده با رده قبلی بوجود میآید:
فراوانی نسبی-تجمعی
ستون «فراوانی نسبی-تجمعی» (Cumulative Relative Frequency) درست به مانند ستون فراوانی تجمعی، از حاصل جمع فراوانی نسبی ردههای قبلی و رده انتخابی ایجاد میشود. برای مثال به منظور محاسبه فراوانی نسبی-تجمعی رده سوم کافی است فراوانی نسبی رده اول، دوم و سوم را با هم جمع کنیم. یا مجموع مقدار فراوانی نسبی-تجمعی رده دوم را با مقدار فراوانی نسبی رده سوم بدست آوریم.
در نتیجه همان روابطی که بین فراوانی تجمعی و فراوانی وجود داشت، برای فراوانی نسبی-تجمعی و فراوانی نسبی نیز وجود دارد.
,
در انتهای ستون فراوانی تجمعی و ستون فراوانی نسبی-تجمعی، جمع قرار نمیگیرد. دیگر آنکه همیشه فراوانی تجمعی رده اول با فراوانی رده اول برابر است و فراوانی نسبی-تجمعی برای رده اول نیز با فراوانی نسبی رده اول یکسان است.
نکته: اگر جدول فراوانی مربوط به متغیر کیفی از نوع اسمی باشد، معمولا از ستونهای فراوانی تجمعی و فراوانی نسبی-تجمعی استفاده نمیکنند.
مثال 1- جدول فراوانی داده کیفی (اسمی)
گروه خون برای ۱۰ نفر از دانشجویان به صورت AB,A,A,B,B,O,B,O,O,O ثبت شده است. جدول فراوانی برای این افراد براساس گروه خون به صورت زیر است.
| شماره ردیف | رده (گروه خونی) | فراوانی | فراوانی نسبی |
| 1 | A | 2 | |
| 2 | B | ۳ | |
| ۳ | O | 4 | |
| ۴ | AB | 1 | |
| جمع | 10 | 1 | |
برطبق این جدول میتوان به سوالات زیر پاسخ داد:
۱- چند درصد از دانشجویان دارای گروه خونی O هستند؟ ۴۰٪
۲- چه تعداد دارای گروه خونی AB هستند؟ ۱ نفر
۳- اگر یک نمونه ۲۰۰ نفری داشتیم، انتظار دارید چه تعدادی دارای گروه خونی B باشند؟ 0.3×200=60 نفر
۴- نما (بیشترین تکرار) برای گروههای خونی مربوط به چه گروهی است؟ گروه خونی O دارای فراوانی ۴ است و بیشترین فراوانی را دارد. پس نما یا مد محسوب میشود.
نکته: با توجه به این که گروه خونی یک متغیر کیفی از نوع اسمی است، ترتیبی برای مقدارهای آن نمیتوان در نظر گرفت. پس ممکن است جای ردیفها را در جدول تغییر داد بدون آنکه در اطلاعاتی که جدول به ما میدهد تغییری بوجود آید.
گاهی براساس جدول فراوانی، نمودار فراوانی یا بافتنگار نیز رسم میکنند.
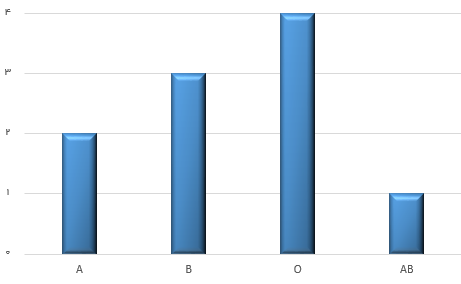
مثال 2- جدول فراوانی داده کیفی (ترتیبی)
مدرک تحصیلی ۲۰ کارمند یک شرکت به صورت زیر جمعآوری شده است.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| کاردانی | کاردانی | کاردانی | کاردانی | کارشناسی ارشد | دیپلم | کاردانی | دیپلم | کارشناسی ارشد | کاردانی |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| دیپلم | دکتری | کارشناسی | دکتری | کارشناسی | کاردانی | کارشناسی | کاردانی | کارشناسی | کارشناسی ارشد |
با توجه به اینکه این دادهها از نوع ترتیبی هستند، همه ستونهای جدول فراوانی برای آن باید نمایش داده شود. جدول فراوانی برای این دادهها در ادامه قابل رویت است.
| شماره ردیف | رده (مدرک تحصیلی) | فراوانی | فراوانی نسبی | فراوانی تجمعی | فراوانی نسبی-تجمعی |
| ۱ | دیپلم | 3 | 0.15 | 3 | 0.15 |
| ۲ | کاردانی | 8 | 0.40 | 11 | 0.55 |
| ۳ | کارشناسی | 4 | 0.20 | 15 | 0.75 |
| ۴ | کارشناسی ارشد | 3 | 0.15 | 18 | 0.95 |
| ۵ | دکتری | 2 | 0.1 | 20 | 1 |
| جمع | 20 | 1 | |||
در زیر بافتنگار مربوط به مدارک کارمندان شرکت برحسب جدول فراوانی ترسیم شده است.

با استفاده از این جدول میتوان به سوالاتی به شکل زیر پاسخ داد:
۱- چند نفر دارای مدرک کارشناسی هستند؟ ۴ نفر
۲- چند نفر از کارمندان مدرک زیر کارشناسی ارشد دارند؟ ۱۵ نفر
۳- چند درصد از کارمندان بالای دیپلم هستند؟ پس 85٪ از کارمندان مدرک تحصیلی بالاتر از دیپلم دارند.
۴- چند نفر از کارمندان مدرک کاردانی تا کارشناسی ارشد دارند؟ با دو روش میتوان به این سوال پاسخ داد: الف- فراوانی کاردانی+فراوانی کارشناسی+فراوانی کارشناسی ارشد=8+4+3=15. ب- تفاضل فراوانی تجمعی کارشناسی ارشد با دیپلم که به صورت 3-18=15 محاسبه میشود.
۵- بیشترین فراوانی (نما) مربوط به کدام مدرک تحصیلی است؟ با توجه به حداکثر فراوانی (مقدار ۸) که مربوط به مدرک کاردانی است، مشخص میشود که نما برای مدارک تحصیلی، کاردانی است.
۶- میانه برای مدرکهای تحصیلی کدام است؟ با توجه به اینکه در ستون فراوانی نسبی-تجمعی اولین ردهای که مقدارش بزرگتر یا مساوی با ۵۰٪ است مربوط به مدرک کاردانی میشود، نتیجه میگیریم که مدرک کاردانی میانه مدرک کارمندان شرکت است.
نکته: فراوانی تجمعی رده آخر همیشه برابر با n و فراوانی تجمعی نسبی رده آخر نیز همیشه برابر با ۱ خواهد بود.
برای تشکیل جدول فراوانی برای دادههای کمی، باید آنها را طبقهبندی کرد. ممکن است از قبل، دادهها به صورت طبقهبندی شده ارائه شوند. در این حالت کافی است طبقهها را در جدول فراوانی قرار داده و محاسبات مربوط به جدول فراوانی را انجام دهیم.
مثال 3- جدول فراوانی داده گسسته
در این مثال با اطلاعات مربوط به تعداد فرزندان ۵۰ خانوار روستایی سروکار داریم و باید برای آنها جدول فراوانی تشکیل دهیم. این اطلاعات به صورت زیر است.
| 0 | 0 | 1 | 1 | 1 | 2 | 2 | 0 | 0 | 2 |
| 3 | 4 | 4 | 3 | 4 | 4 | 3 | 4 | 4 | 3 |
| 4 | 3 | 5 | 6 | 5 | 6 | 5 | 6 | 5 | 6 |
| 7 | 7 | 5 | 6 | 7 | 7 | 5 | 6 | 5 | 6 |
| 5 | 6 | 5 | 6 | 5 | 6 | 5 | 5 | 5 | 5 |
با توجه به مقدارهای مختلف برای تعداد فرزندان مشخص است که جدول فراوانی باید دارای ۸ رده باشد. ولی با استفاده از طبقهبندی و ایجاد دستههای مختلف میتوان جدول فراوانی با ردههای کمتر ایجاد کرد. جدول فراوانی برای تعداد فرزندان ۵۰ خانوار روستایی با ۵ رده به صورت زیر خواهد بود.
| شماره ردیف | حدود رده | فراوانی | فراوانی نسبی | فراوانی تجمعی | فراوانی نسبی-تجمعی |
| ۱ | 0 | 4 | 8٪ | 4 | ۸٪ |
| 2 | 1-2 | 6 | 12٪ | 10 | 20٪ |
| 3 | 3-4 | 12 | 24٪ | 22 | 44٪ |
| 4 | 5-6 | 24 | 48٪ | 46 | 92٪ |
| 5 | ۷ و بیشتر | 4 | 8٪ | 50 | 100٪ |
| جمع | 50 | 100٪ | |||
در زیر بافتنگار مربوط به تعداد فرزندان خانوارها برحسب جدول فراوانی ترسیم شده است.
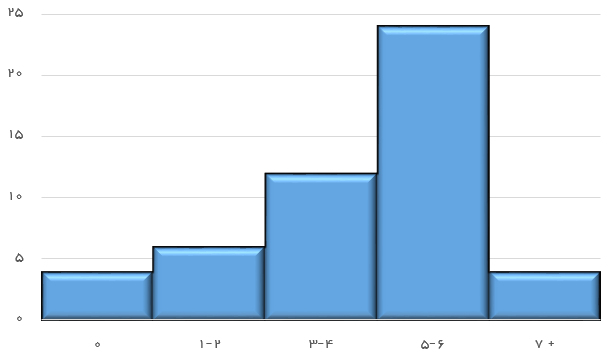
۱- تعداد خانوارهایی که دارای ۵ یا ۶ فرزند هستند؟ ۲۴ خانوار.
۲- درصد خانوارهایی که دارای ۳ یا ۴ فرزند هستند؟ ۲۴٪.
۳- تعداد خانوارهایی که کمتر از ۵ فرزند دارند؟ ۲۲ خانوار.
۴- درصد خانوارهایی با بیش از ۵ فرزند؟ با دو روش میتوان به سوال پاسخ داد: الف-براساس تفاضل فراوانی نسبی-تجمعی ۴۴٪-۱۰۰٪=56٪ (منظور از ۱۰۰٪ همان فراوانی نسبی-تجمعی رده آخر است). ب- براساس مجموع فراوانیهای نسبی 48٪+8٪=56٪.
۵- اگر روستایی دیگر با ۱۰۰ خانوار، دارای توزیع فرزندان به مانند همین روستا باشد، انتظار دارید خانوارهای با ۵ یا ۶ فرزند چه تعداد باشند؟ 48٪×100= ۴۸ خانوار.
6- کدام رده دارای بیشترین فراوانی است؟ با توجه به نمودار و جدول فراوانی مشخص است که خانوارهایی با ۵ یا ۶ فرزند، نما هستند.
۷- کدام رده شامل میانه تعداد فرزندان است؟ از آنجایی که اولین رده در ستون فراوانی نسبی-تجمعی که مقدارش بیشتر یا مساوی ۵۰٪ است مربوط به رده خانوارهایی با تعداد فرزند ۵ یا ۶ است، میانه رده چهارم خواهد بود.
۸- به طور متوسط تعداد فرزندان هر خانوار در این روستا چقدر است؟ اگر برای هر رده، وسط حدود رده را به عنوان نماینده آن رده با علامت در نظر بگیریم و ستون فراوانی نسبی را به عنوان وزن هر نماینده رده محسوب کنیم، میانگین را میتوان به صورت زیر محاسبه کرد:
در نتیجه هر خانوار در این روستا به طور متوسط حدود ۴ فرزند دارد.
مثال 4- جدول فراوانی داده کمی (پیوسته)
وزن یک نمونه ۵۰ تایی از قوطیهای رب گوجه در یک فایل اطلاعاتی با قالب اکسل ثبت شده است. فایل اکسل حاوی این اطلاعات را میتوانید از اینجا دریافت کنید. از آنجایی که این وزنها با دقت گرم ثبت شدهاند، برای طبقهبندی آنها مراحل زیر را طی میکنیم.
۱- ابتدا دامنه تغییرات را برای دادهها محاسبه میکنیم ولی از آنجایی که دادهها با دقت ۱ گرم ثبت شدهاند ممکن است مقداری که برای بزرگترین وزن به ما داده شده (یعنی 510.0) کمی بیشتر بوده که در اثر گرد شدن به این مقدار 510.0 رسیده است.

همچنین کمترین مقدار که برابر با 491 گرم است ممکن است در اثر گرد کردن مقداری مثلا 490.6 بدست آمده باشد. بنابراین در چنین حالتی اگر p برابر میزان دقت اندازهگیری باشد، مقدار به بزرگترین مقدار اضافه و از کوچکترین مقدار کسر میکنیم و سپس دامنه تغییرات را بدست میآوریم. این مقدار برآورد بهتری برای دامنه تغییرات است.
به این ترتیب خواهیم داشت:
حال اگر قرار باشد وزن قوطیها را براساس ۵ رده، طبقهبندی کنیم، طول رده برابر خواهد بود با گرم. پس برای مثال کرانهای مربوط به رده اول به صورت و برای رده دوم نیز خواهد بود.
۲- براساس حدود هر طبقه، دادههای مربوطه را شمارش میکنیم و در ستون فراوانی قرار میدهیم.
۳- محاسبات برای ستونهای دیگر را برمبنای ستون فراوانی تکمیل میکنیم.
۴ برای چک کردن صحت انجام محاسبات، جمع ستونی فراوانی را با اندازه نمونه (۵۰) و جمع ستون فراوانی نسبی را با ۱ یا ۱۰۰٪ مقایسه میکنیم.
حال براساس این طبقهبندی، جدول فراوانی را تشکیل میدهیم.
| شماره ردیف | حدود رده یا طبقه | فراوانی | فراوانی نسبی | فراوانی تجمعی | فراوانی نسبی-تجمعی |
| 1 | 10 | 20٪ | 10 | 20٪ | |
| 2 | 8 | 16٪ | 18 | 36٪ | |
| ۳ | 10 | 20٪ | 28 | 56٪ | |
| ۴ | 13 | 26٪ | 41 | 82٪ | |
| ۵ | 9 | 18٪ | 50 | 100٪ | |
| جمع | 50 | 100٪ | |||
در زیر بافتنگار مربوط به وزن قوطیهای گوجه فرنگی برحسب جدول فراوانی ترسیم شده است.

با استفاده از این جدول میتوان به سوالات زیر پاسخ داد:
۱- چند قوطی وزنی کمتر از 502.5 گرم دارند؟ 28 قوطی
۲- چند درصد قوطیها وزنی بین 498.5 تا 502.5 دارند؟ 20٪
3- چند درصد قوطیها از 502.5 گرم وزنی بیشتری دارند؟ به دو روش میتوان پاسخ داد. یا فراوانی نسبی-تجمعی 56٪-100٪=44٪ یا با فراوانی نسبی 18٪+26٪=44٪
4- چه حدود وزنی بیشترین فراوانی را دارد؟ با توجه به حداکثر میزان فراوانی که برابر با ۱۳ است متوجه میشویم که بیشترین فراوانی در حدود وزنی 502.5 تا 506.5 گرم است.
5- نما برای وزن قوطیهای رب گوجه چند گرم است؟ با توجه به نمودار یا ستون فراوانی مشخص میشود که رده 4 نما محسوب میشود، یا میتوان گفت که نما در بین دو مقدار 502.5 تا 506.5 قرار دارد.
6- میانه برای وزن قوطیهای رب گوجه چند گرم است؟ با توجه به ستون فراوانی نسبی-تجمعی مشخص است که اولین ردهای که مقدار فراوانی نسبی-تجمعی آن بزرگتر یا مساوی با ۵۰٪ است، رده سوم است پس میانه در این رده قرار دارد. یا میتوان گفت که میانه در بین دو مقدار 498.5 تا 502.5 قرار دارد.
7- میانگین و انحراف معیار وزن قوطیهای رب گوجه چقدر است؟ به منظور محاسبه این پارامترها بهتر است از یک جدول کمکی بهره گرفت. این جدول در ادامه دیده میشود. برای محاسبه ستون نماینده رده از وسط حدود رده استفاده شده است. مجموع حاصل ضرب فراوانی نسبی در مقدار نماینده رده نیز میانگین وزن را محاسبه میکند که برابر با 500.74 گرم است.
| حدود رده | ||||||
| 492.5 | 10 | 0.2 | 0.2×492.5=98.5 | 13.58 | ||
| 496.5 | 8 | 0.16 | 0.16×496.5=79.44 | 2.88 | ||
| 500.5 | 10 | 0.2 | 0.2×500.5=100.1 | 0.01 | ||
| 504.5 | 13 | 0.26 | 0.26×504.5=131.17 | 3.68 | ||
| 508.5 | 9 | 0.18 | 0.18×508.5=91.53 | 10.84 | ||
| جمع | 50 | 1 | 500.74 | 160.3 | 30.99 | |
برای محاسبه انحراف معیار هم تفاضل مقدار نماینده ردهها از میانگین محاسبه شده و به توان ۲ رسیده است. مجموع حاصلضرب این مقدارها در فراوانی نسبی، واریانس را نشان میدهد. در این حالت مقدار واریانس برابر با 30.99 گرم مربع است. با جذر گرفتن از واریانس، انحراف معیار پیدا میشود. پس مقدار انحراف معیار بر اساس جدول فراوانی برابر با 5.57 گرم خواهد بود.
آزمون جدول فراوانی
۱. کدام ویژگی جدول فراوانی باعث میشود توزیع دادههای کیفی بهتر از معیارهایی مانند میانگین یا میانه دیده شود؟
دستهبندی و نمایش تعداد هر مقدار یا طبقه به صورت منظم
امکان محاسبه انحراف معیار برای طبقات
داشتن ستون فراوانی نسبی برای هر رده
نمایش گرافیکی دادهها به کمک هیستوگرام
دلیل اصلی این است که «دستهبندی و نمایش تعداد هر مقدار یا طبقه به صورت منظم» باعث میشود توزیع دادههای کیفی به صورت شفاف قابل مشاهده باشد و همه ردهها بدون توجه به مقدار عددی به خوبی نمایش داده شوند. ستون فراوانی نسبی به درصدها اشاره دارد نه خود توزیع.
۲. چه تفاوتی در ساختار ستون اول جدول فراوانی برای دادههای کیفی نسبت به دادههای کمی دیده میشود؟
در دادههای کیفی ستون اول معمولا نام طبقه یا مقادیر متغیر است، اما در دادههای کمی حدود رده یا بازه عددی قرار میگیرد.
در دادههای کیفی ستون اول فقط شامل درصد است، ولی در دادههای کمی شامل نام طبقات است.
در دادههای کیفی مقدار میانگین در ستون اول میآید، اما در دادههای کمی این مقدار حذف میشود.
در دادههای کیفی همیشه ستون اول کدهای عددی دارد، ولی در دادههای کمی این کدها وجود ندارد.
در جدول فراوانی، برای دادههای کیفی، ستون اول معمولا نام طبقه یا خود مقادیر متغیر همچون گروه خونی یا سطح تحصیلات را نشان میدهد. اما برای دادههای کمی، ستون اول شامل حدود ردهها یا بازههای عددی مثل بازه سنی یا وزن میشود. بنابراین، متن «در دادههای کیفی ستون اول معمولا نام طبقه یا مقادیر متغیر است، اما در دادههای کمی حدود رده یا بازه عددی قرار میگیرد» درست است. سایر گزینهها نادرست هستند زیرا ستون اول معمولا درصد یا مقدار میانگین را نشان نمیدهد و استفاده از کدهای عددی در دادههای کیفی همواره الزامی نیست.
۳. کدام رابطه برای محاسبه فراوانی نسبی یک رده در جدول فراوانی درست است و مجموع فراوانیهای نسبی چه تفسیری دارد؟
نسبت تعداد افراد هر رده به مجموع کل مشاهدات است و مجموع آنها باید برابر با ۱ یا ۱۰۰٪ باشد.
تفاضل فراوانی تجمعی و فراوانی نسبی همان رده است و مجموع آن برابر با تعداد طبقات است.
جمع فراوانی مطلق با فراوانی تجمعی هر رده محاسبه میشود و مجموع آنها همیشه بیش از ۱ است.
نسبت تعداد کل مشاهدات به تعداد طبقات است و مجموع آن میتواند متفاوت باشد.
فرمول صحیح برای فراوانی نسبی هر رده، نسبت تعداد افراد یا موارد موجود در آن رده به کل مشاهدات است؛ یعنی تقسیم فراوانی رده () بر تعداد کل دادهها (n) که برابر با خواهد بود. مجموع این فراوانیهای نسبی تمام ردهها باید همواره برابر با ۱ (یا به صورت درصد، ۱۰۰٪) باشد.
۴. در هنگام ساخت جدول فراوانی برای دادههای کمی پیوسته، چرا تعیین دقیق طول رده اهمیت دارد و این کار چه اثری بر نتایج تحلیل دادهها خواهد داشت؟
اگر طول رده یکسان نباشد، ترتیب ردهها برای تحلیل توزیع اهمیت ندارد.
تعیین طول رده فقط در دادههای کیفی استفاده میشود و برای کمی پیوسته لازم نیست.
تعیین طول رده مناسب باعث افزایش دقت محاسبه میانگین و نمای داده میشود.
طول رده اشتباه تنها روی فراوانی نسبی تاثیر دارد و به نتایج کلی آسیب نمیزند.
انتخاب طول رده مناسب برای دادههای کمی پیوسته باعث میشود که تفسیر شاخصهایی مانند میانگین، میانه و نما دقیقتر انجام شود و توزیع و پراکندگی داده به شکل واقعی نمایش داده شود. اگر طول رده به درستی تعیین نشود، مثلا ردهها خیلی کوتاه یا خیلی بلند باشند، شاخصهای آماری و تحلیل توزیع دچار خطا میشود و نتایج گمراهکننده بهدست میآید.
۵. اگر در جدول فراوانی مدرک تحصیلی کارکنان، ستون فراوانی تجمعی حذف شود، چه نوع تحلیل یا محاسبهای دچار اشکال خواهد شد؟
یافتن میانه مدرک تحصیلی
محاسبه فراوانی نسبی برای هر رده
تعیین گروه با بیشترین نما
محاسبه میانگین مدرکها
بدون ستون «فراوانی تجمعی» نمیتوان نقطه وسط توزیع را به درستی مشخص کرد و لذا «یافتن میانه (Median) مدرک تحصیلی» مشکل میشود.
۶. برای محاسبه درصد خانوارهایی که تعداد فرزند آنها بیش از میانه است در جدول فراوانی گسسته، کدام روش مبتنی بر فراوانی نسبی صحیح است؟
جمع فراوانی نسبی ردههای بالاتر از رده میانه را محاسبه کنیم.
جمع فراوانی نسبی ردههای مساوی یا کمتر از میانه را به کار ببریم.
فراوانی نسبی رده میانه را فقط در نظر بگیریم.
میانگین تمام فراوانیهای نسبی را محاسبه کنیم.
برای تعیین درصد خانوارهایی که تعداد فرزند بیشتری از میانه دارند، باید مجموع فراوانی نسبی ردههایی که تعداد فرزندشان بالاتر از رده میانه است را حساب کنیم. این مقدار نشاندهنده بخشی از خانوارها با تعداد فرزند بالاتر از حد وسط توزیع است.
۷. در جدول فراوانی برای دادههای کیفی اسمی، اگر ترتیب سطرهای طبقات مختلف تغییر کند، کدام ویژگی جدول یا نتیجه آماری بدون تغییر باقی میماند؟
مقدار نما ثابت باقی میماند.
تعداد کل افراد هر طبقه تغییر نمیکند.
درصد هر گروه خونی تغییر نمیکند.
فراوانی نسبی هر طبقه تغییری ندارد.
در جدول فراوانی برای دادههای کیفی اسمی، جابهجایی سطرهای طبقات اثری بر مقدار نما ندارد، زیرا نما همواره طبقهای با بیشترین فراوانی است، صرفنظر از اینکه آن طبقه در کدام سطر جدول قرار گرفته باشد.













سلام
اون جدول مدارک تحصیلی چند نفر زیر کارشناسی ارشد میشه 15 دیگه نه 18
با سلام خدمت شما؛
نکته بیان شده درست است و تصحیحات لازم در متن اعمال شد.
از همراهی شما با مجله فرادرس سپاسگزاریم.
تشکر از توضيحات جامع و خوب به زبان فارسی- منبع فارسي خوب خیلی کمه
👌🏻👌🏻👌🏻👌🏻
سلام وقت تون بخیر
فراوانی تراکمی در صورتی که فراوانی و مجموع فراوانی های توزیع و دامنه ی طبقه بیان شده چگونه حساب می شود؟
بسیار عالی
خیلی ممنون از شما
بقیه سایتا r و s رو بررسی نکرده بودند ولی شما بررسی کردید و مشکلم حل شد🙏
با سلام درس فراوانی خیلی مفید بود ممنون
من رشته کارشناسی مکانیک بود و برای پایان نامه کارشناسی ارشد در رشته صنایع از درسهای شما استفاده می کنم خیلی مفید است.
سلام و عرض ادب
معدل چه نوع متغییری است؟
سلام معدل از نوع پیوسته هستش
سلام تشکر ولی یک سوال دارم منظور از جدول توزیع فراوانی طبقه بندی نشده چیست و چه کاربردی دارد؟
طی دوران کرونا همگی مجبور شدیم به آموزش مجازی.متاسفانه برای من درس آمار بسیار سخت بود و استاد خوبی هم نداشتیم.با آموزش های فرادرس متوجه شدم که نه تنها شیوه تدریس و بیان استاد بسیار در فهم مطلب مهم هست بلکه تصور من در مورد خنگ بودنم در ریاضی و آمار به کلی درهم شکست.نمیدونم این کامنت دیده میشه اصلا یانه ولی واقعا ممنون ازت فرادرس و استادان عزیز.
خیلی ممنونم از اموزش مفید و خوبتون ???????
مطلبی که آموزش داده میشه خیلی خوبه و راحت میشه فهمید فقط صدای موزیک خیلی زیاده و موضوع ریاضی با این زمینه موزیک باعث اعصاب خوردی میشه
سایتتون عالیه..فوق العاده
تشکر مفید بود
باتشكر از توضيحات بسيار خوبتون