تکنیک Folding در جاوا — به زبان ساده

این راهنما به بررسی تکنیکهای هش کردن اختصاص دارد که در ساختمانهای داده مختلف برای ایجاد زمان دسترسی ثابت به عناصرشان استفاده میشوند. در این مقاله به بررسی جزییات تکنیک Folding در جاوا میپردازیم و مقدمهای کوتاه در مورد تکنیکهای mid-square و «بستهبندی» (binning) ارائه میکنیم.
مقدمه
زمانی که ساختمانهای دادهای برای ذخیرهسازی اشیا انتخاب میکنیم، یکی از ملاحظات این است که آیا باید به سرعت به آنها دسترسی پیدا کنیم یا نه. پکیج کاربردی جاوا ساحتمان های داده زیادی برای ذخیرهسازی شیءها در اختیار ما قرار میدهد. چنان که میدانیم برخی از این ساختمانهای داده امکان بازیابی عناصرشان را در زمان ثابتی در اختیار ما قرار میدهند و مهم نیست که تعداد عناصر داخلشان چه قدر است.
احتمالاً سادهترین ساختمان داده، آرایه است. در واقع ما از طریق اندیس عناصر در آرایه به آنها دسترسی پیدا میکنیم. از این رو زمان دسترسی به طور طبیعی به اندازه آرایه بستگی ندارد. ساختمانهای داده زیادی در پشت صحنه از آرایهها استفاده میکنند. مشکل این است که اندیسهای آرایه باید عددی باشند، در حالی که در اغلب موارد دستکاری این ساختمانهای داده با اشیا ترجیح بیشتری دارد.
برای حل این مشکل بسیاری از ساختمانهای داده تلاش میکنند یک مقدار عددی انتساب دهند که به عنوان یک اندیس آرایه برای اشیا عمل میکند. ما این مقدار را یک مقدار هش یا صرفاً هش (hash) مینامیم.
هش کردن
هش کردن به معنی تبدیل یک شیء به یک مقدار عددی است. تابعهایی که این تبدیلها را اجرا میکنند به نام توابع هش نامیده میشوند. به منظور سادهتر کردن موضوع تصور کنید تابعهای هش رشتهها را به اندیسهای آرایه تبدیل میکنند، یعنی به اعداد صحیح در بازه [0, N] تبدیل میشوند که N متناهی است.
به طور طبیعی یک تابع هش روی طیف وسیعی از رشتهها اعمال میشود. از این رو مشخصههای global آن مهم میشوند.
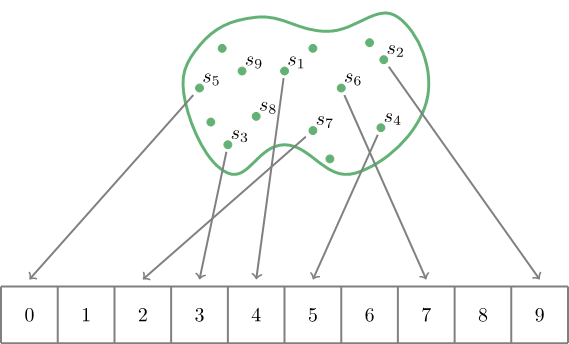
متأسفانه امکان این که یک تابع هش رشتههای مختلف را به اعداد متفاوت هش کند وجود ندارد. این امکان وجود دارد که تعداد رشتهها بسیار بزرگتر از تعداد اعداد صحیح در هر بازه [0, N] باشد. در این حالت ناگزیر یک جفت رشته نابرابر وجود خواهند داشت که برای آنها مقادیر هش برابری تولید میشود. این پدیده به نام «تصادم» (collision) شناخته میشود.
ما قصد نداریم وارد جزییات مهندسی که در پس تابعهای هش وجود دارد بشویم، اما روشن است که یک تابع هش خوب باید تلاش کند رشتههایی که روی آنها تعریف میشود را به صورت یکنواختی به اعداد نگاشت کند. الزام بدیهی دیگر این است که تابع هش خوب باید سریع باشد. اگر محاسبه مقدار هش زمان زیادی طول بکشد، در این صورت نمیتوانیم به سرعت به عناصر خود دسترسی پیدا کنیم.
در این راهنما به بررسی یکی از تکنیکهایی میپردازیم که برای نگاشت یکنواخت در عین حفظ سرعت تبدیل استفاده میشود.
تکنیک Folding در جاوا
هدف ما یافتن تابعی است که رشتهها را به اندیسهای آرایه تبدیل کند. برای نمایش این ایده فرض کنید که میخواهیم این آرایه ظرفیتی برابر با 5^10 عنصر داشته باشد و از زبان جاوا به عنوان یک مثال استفاده میکنیم.
توصیف
کار خود را با تبدیل کاراکترهای رشته به عدد آغاز میکنیم. ASCII گزینه خوبی برای این عملیات است.
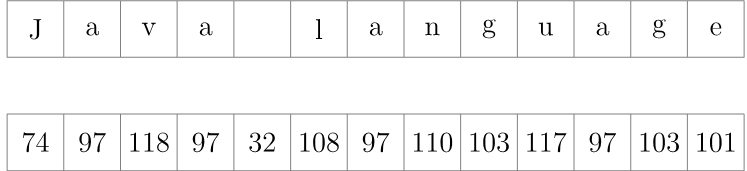
اکنون اعدادی را که به دست آمده در گروههای با اندازه یکسان میچینیم. به طور کلی ما مقدار اندازه گروه را بر اساس اندازه آرایه خود انتخاب میکنیم که 5^10 است. از آنجا که اعدادی که رشتهها را به آنها تبدیل کردیم شامل دو تا سه رقم هستند، بدون از دست دادن تعمیمپذیری قضیه میتوانیم اندازه گروه را روی دو تنظیم کنیم:

گام بعدی این است که اعداد را در هر گروه طوری تجمیع کنیم که گویی رشته هستند و مجموعشان را پیدا کنیم:

اکنون باید گام نهایی را برداریم. بررسی میکنیم که آیا تعداد 348933 میتواند به عنوان یک اندیس برای آرایه با اندازه 5^10 عمل کند یا نه. به طور طبیعی این عدد از بیشینه مقدار مجاز یعنی 99999 بیشتر است. با بهکارگیری عملگر همنهشتی برای یافتن نتیجه نهایی به صورت زیر میتوان به سادگی بر این مشکل غلبه کرد:
348933% 10000 = 48933
توضیح نهایی
چنان که دیدیم این الگوریتم شامل هیچ عملیات زمان بری نیست و از این رو کاملاً سریع است. هر کاراکتر رشته ورودی در نتیجه نهایی دخیل است. این واقعیت قطعاً به ما کمک میکند که تصادمها کاهش دهیم، اما از پیچیده شدن آنها جلوگیری نمیکند.
برای نمونه اگر بخواهیم از folding اجتناب کنیم و عملگر همنهشتی را مستقیماً روی رشته ورودی با قالببندی ASCII عمال کنیم، با نادیده گرفتن مشکل سرریز نتیجه زیر به دست میآید:
749711897321089711010311797103101% 100000 = 3101
در این صورت چنین تابعی میتواند مقدار یکسانی را برای همه رشتههای ورودی که دو کاراکتر پایانی یکسانی دارند برای نمونه برای age ،page ،large و غیره ایجاد کند.
از روی توصیف الگوریتم میدانیم که مصون از بروز تصادم نیست. برای نمونه الگوریتم مقدار هش یکسانی برای دو رشته Java language و vaJa language تولید میکند.
تکنیکهای دیگر
تکنیک Folding کاملاً رایج است، اما تنها گزینه رایج محسوب نمیشود. برخی اوقات تکنیکهای binning یا mid-square نیز میتوانند مفید باشند.
ایده این الگوریتم را نه با رشتهها بلکه با اعداد نمایش میدهیم. فرض کنید که قبلاً رشتهها را به اعداد تبدیل کردهایم. همچنین قصد نداریم مزایا و معایب آنها را مورد بررسی قرار دهیم، بلکه میخواهیم ایدهای کلی در مورد این الگوریتمها به دست بیاورید.
تکنیک Binning
فرض کنید 100 عدد صحیح داریم و میخواهیم تابع هش ما آنها را به آرایهای از 10 عنصر نگاشت کند. سپس آن 100 عدد را در 10 گروه طوری قرار میدهیم که ده عدد نخست در «گروه» (bin) اول، ده عدد دوم در گروه دوم و همین طور تا آخر جای بگیرند:
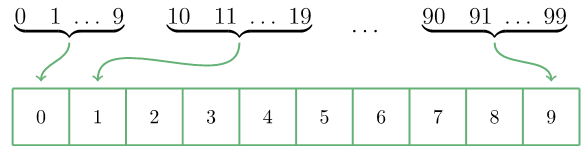
تکنیک Mid-Square
این الگوریتم از سوی جان فن نیومن پیشنهاد شده و امکان تولید اعداد شبه تصادفی را میدهد که از عدد خاصی آغاز میشوند.
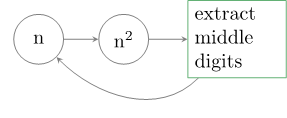
این الگوریتم را با یک مثال مناسب توضیح میدهیم. فرض کنید یک عدد چهاررقمی به صورت 1111 داریم. بر اساس این الگوریتم آن را به توان 2 میرسانیم. بدین ترتیب عدد 1234321 به دست میآید. برای نمونه چهار رقم میانی را استخراج میکنیم که 2343 است. این الگوریتم امکان تکرار این فرایند را تا زمانی که نتیجه مطلوب به دست آید فراهم کرده است.
سخن پایانی
در این راهنما چند تکنیک هش را مورد بررسی قرار دادیم. تکنیک folding را به تفصیل بررسی کردیم و توضیح کوتاهی در مورد تکنیکهای binning و mid-square ارائه نمودیم. کدهای کامل الگوریتمهای معرفی شده در این مقاله را میتوانید در این صفحه (+) مشاهده کنید.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای زبان برنامهنویسی جاو
- مجموعه آموزشهای برنامهنویسی
- آموزش مروری بر توابع Hash و خطر تصادم در آنها
- جدول Hash — به زبان ساده
- تابع هش یا درهم سازی (Hash Function) چیست؟ — به زبان ساده
==










