رسم شکل با الگوریتم خط Bresenham و کدنویسی جاوا اسکریپت – راهنمای کاربردی

یک مساله جدید همیشه با یک پرسش آغاز و در پی آن برای حل مساله به دنبال راهکار گشته می‌شود. برای کدنویسی الگوریتم‌ها در هر حوزه‌ای نیز این امر صادق است. در این مطلب، چگونگی کدنویسی یک الگوریتم ترسیم خط برای افراد مبتدی از زمان طرح پرسش تا پیاده‌سازی الگوریتم آموزش داده خواهد شد. پرسشی که در اینجا و برای مساله مورد بررسی در این مطلب مطرح می‌شود این است که «چگونه می‌توان یک خط را روی صفحه نمایش کامپیوتر بدون استفاده از Canvas (کتابخانه HTML5) یا کتابخانه‌های زبان‌های برنامه‌نویسی ترسیم کرد؟». در ادامه از «الگوریتم خط Bresenham» (یا Bresenham's Line Algorithm) برای پاسخ‌گویی به این پرسش استفاده می‌شود.

البته، سازندگان HTML Canvas ،SVG ،WebGL و دیگر کتابخانه‌های گرافیکی کدهایی را از پایه برای ترسیم خطوط نوشته‌اند ولی به دلایلی که در ادامه بیان خواهد شد، در این مطلب انجام این کار از پایه و بدون بهره‌گیری از کتابخانه‌های گرافیکی آموزش داده خواهد شد. راهکار مورد استفاده در این راهنما، ترسیم خطوط با استفاده از مثال الگوریتم خط Bresenham است.

چرا الگوریتم خط Bresenham؟

الگوریتم خط Bresenham به دلایل گوناگونی که برخی از آن‌ها در ادامه ذکر شده‌اند، گزینه خوبی برای یادگیری چگونگی ترسیم خطوط از پایه به شمار می‌آید.

فیلم آموزش گرافیک کامپیوتری + مفاهیم کلیدی در فرادرس

کلیک کنید

1. فقط با اعداد کار نمی‌شود و خروجی بصری نیز ارائه می‌شود.
2. برای یادگیری افراد مبتدی به دلیل سادگی که دارد گزینه مناسبی محسوب می‌شود.
3. از «دستگاه مختصات دکارتی» (Cartesian Coordinate System) استفاده می‌کند که مبنایی مناسب برای بسیاری از الگوریتم‌ها است.
4. می‌توان آن را در جاوا اسکریپت پیاده‌سازی کرد.

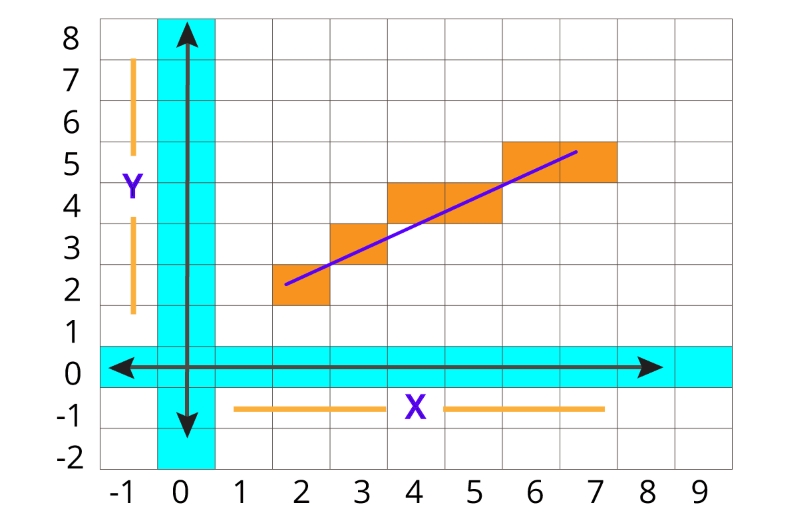
انیمیشن موجود در بالا حاصل الگوریتمی است که در این راهنما تشریح شده. یک خط بین دو نقطه در یک گرافیک شطرنجی متداول ترسیم شده. در این مثال، از شبکه HTML ساده ساخته شده از عناصر DIV استفاده شده است. این شبکه کُند محسوب می‌شود و برای رندرینگ گرافیکی با کارایی بالا در زمان واقعی مناسب محسوب نمی‌شود اما به وضوح هدف این الگوریتم را نشان می‌دهد.

روش کار الگوریتم

ابتدا، بهتر است که آنچه مقرر شده انجام شود را بصری‌سازی کرد. الگوریتم خط Bresenham مساله حل خطوط در یک چهارم اول را حل کرده است.

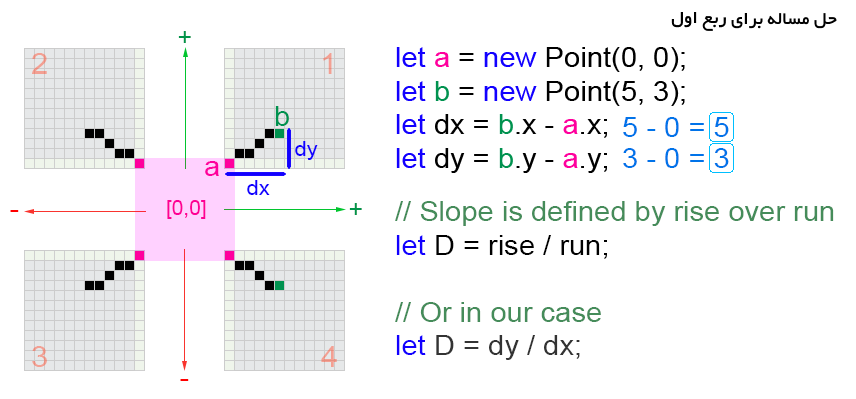
ترسیم یک خط در هر جهتی نیازمند توجه به ربع‌های دستگاه مختصات است. در حالیکه الگوریتم برای ربع اول آسان است، پیاده‌سازی برای همه ربع‌ها و نیم‌ربع‌ها به تلاش بیشتری به لحاظ منطقی نیاز دارد. سایر موارد، در واقع موارد ساده‌ای از تصاویر آینه‌ای دو نیم‌ربع واقع در ربع اول هستند. این یعنی به جای اختراع مجدد چرخ، می‌توان برخی از متغیرهای را تغییر دارد. اکنون، پرسشی که مطرح می‌شود این است که چگونه می‌توان چنین چیزی را در جاوااسکریپت کدنویسی کرد.

چرا ترسیم خطوط در HTML بدون استفاده از Canvas؟

دلایل زیادی برای انجام این کار وجود دارد. از جمله این موارد می‌توان به ارائه توصیفی کوتاه از چگونگی عملکرد الگوریتم خط Bresenham اشاره کرد. ترسیم خط در HTML بدون استفاده از Canvas یا WebGl کاری ساده و جالب است. در این راهنما از یک کلاس جاوا اسکریپت استفاده می‌شود که کار نمونه‌گیری از یک خط HTML را مدیریت می‌کند. می‌توان این کار را برای هر تعداد خطی انجام داد. در بازی‌های کامپیوتری معمولا با ترسیم خطوط سر و کار دارند. اما جدای از آن، ترسیم خطوط در HTML کاری جالب است.

فیلم آموزش گرافیک کامپیوتری + مفاهیم کلیدی در فرادرس

کلیک کنید

البته، سرعت پایین رندرینگ در HTML یک مشکل به حساب می‌آید. اما فراتر از آن، بهینه‌سازی برای به دست آوردن کارایی بیشتر، معنادار است. اما تمرکز این بخش از راهنما توضیح دادن خود الگوریتم ترسیم خط است. همچنین، همیشه می‌توان آن را در هر محیط شطرنجی یا کتابخانه گرافیکی دیگری پیاده‌سازی کرد.

پیاده‌سازی الگوریتم ترسیم خط در جاوا اسکریپت

دو دلتا را به دست آورده و سپس شیب معادله خط بر اساس نقاط ابتدایی و انتهایی خط محاسبه می‌شوند. نقاط آغازین و پایانی هر خط برای چهار پارامتر تابع draw_line مورد نیاز هستند (به ترتیب [x0, y0] و [x1, y1]). می‌توان این مورد را در زبان‌های برنامه‌نویسی دیگر شامل C++ ،C، پایتون و جاوا پیاده‌سازی کرد.

در این راهنما از جاوا اسکریپت استفاده شده. اکنون زمان آن رسیده که منطق حاکم بر انجام این کار به کد تبدیل شود. شبه‌کد مربوط به انجام این کار در ادامه آمده است.

با تبدیل قطعه کد بالا به جاوا اسکریپت، خروجی زیر حاصل می‌شود.

شایان توجه است که آنچه نوشته شده صرفا برای ربع اول بود.

توصیف منطق برنامه

ابتدا، تفاوت بین نقاط ابتدایی و انتهایی خطوط در هر دو محور (dx و dy) به ترتیب برای هر یک از دو بعد باید محاسبه شود که معمولا دلتا نامیده می‌شود. سپس، دلتای خط به طور کلی محاسبه می‌شود (در اینجا در متغیر D ذخیره‌سازی می‌شود). به این مورد می‌توان به صورت معادله ریاضی برای ترسیم خط نگاه کرد. یا به عبارت دیگر، می‌توان آن را معادله شیب خط پنداشت.

فیلم آموزش گرافیک کامپیوتری + مفاهیم کلیدی در فرادرس

کلیک کنید

پیش از تکرار هر بخش از خط، شمارنده محور y باید با تنظیم آن روی موقعیت اولیه خط، «بازنشانی» (reset) شود (که ضمن ترسیم خط با استفاده از یک حلقه For در آن حرکت خواهد شد). در اینجا، y0 به مختصات Y اولین نقطه در خط ارجاع دارد. در نهایت، یک پیکسل از خط در هر زمان ترسیم می‌شود، که در شبه کد به عنوان تابع (pixel(x, y نشان داده شده است. پس از آنکه پیکسل رندر شد، می‌توان موقعیت کنونی پیکسل را با استفاده از گام‌های دلتای محاسبه شده تنظیم کرد.

هر بار که شمارنده دلتا از ۰ فراتر رفت، به پیکسل بعدی در محور Y رفته و متغیر D مجددا تنظیم می‌شود، اما این بار در جهت مخالف، و بدین شکل ترسیم خط در دو بُعد ادامه دارد و با رسیدن به انتهای خط تکمیل می‌شود. اما این همه چیز نیست. بسته به «محور غالب» (Axis-Dominance)، حلقه For برای حرکت در آن جهت باید ویرایش شود. برای تکمیل کردن الگوریتم، باید پارامترها را بسته به اینکه در کدام نیم‌ربع قرار گرفته‌اند تنظیم کرد. این موضوع به طور کامل در بخش بعدی تشریح شده است.

ترسیم همه ۴ ربع / هشت نیم‌ربع

الگوریتم خط Bresenham بالا برای ترسیم خط تنها در یک ربع (ربع اول) دستگاه مختصات دکارتی طراحی شده است. اما نیاز به پوشش دادن همه جهت‌ها در آن وجود دارد. پس از آن، یک خط تصادفی را می‌توان از هر نقطه‌ای در صفحه شطرنجی به هر نقطه دیگری ترسیم کرد. این یعنی علاوه بر شبه کد بالا، نیاز به توجه به دو موضوع است.

فیلم آموزش گرافیک کامپیوتری + مفاهیم کلیدی در فرادرس

کلیک کنید

الگوریتم Quadrant-Aware: الگوریتم باید پارامترهای تکرار کننده را برای هر یک از چهار ربع تنظیم کند. می‌توان نقاط پایانی خط را تغییر داد تا اطمینان حاصل شود که خط همیشه از چپ به راست کشیده می‌شود (خط از نقطه شروع به سمت بالا یا پایین اشاره دارد). همچنین می‌توان در چهار شرایط مختلف برای هر یک از ربع‌ها به ترتیب کار انشعاب را انجام داد و تکرارکننده‌های محور x و y را برای جهت خط تغییر داد.

Axis-Dominance: حتی در هر چهار ربع هم خط در محور غالب x و یا y خواهد بود. این یعنی نه چهار، بلکه هشت شرایط مختلف وجود دارد. در واقع یکی برای هر یک از هشت نیم‌ربع موجود است. خوشبختانه، الگوریتم دقیقا مشابه خواهد بود و تنها کار مورد نیاز تغییر دادن تکرارها و چندین بار انشعاب است.

این میزان از انشعاب بسیار زیاد محسوب می‌شود، اما الگوریتم ارائه شده در مثال بعدی، همه شرایط ممکن را مد نظر قرار خواهد داد.

الگوریتم خط Bresenham در جاوا اسکریپت

در ادامه، کد جاوا اسکریپت کامل مورد نیاز برای انجام آنچه پیش‌تر بیان شد، ارائه شده است.

آنچه بیان شد تنها یکی از راه‌های نوشتن الگوریتم خط Bresenham است. می‌توان با انجام بررسی‌های بیشتر و تغییر پارامترها و انجام اصلاحات روی شاخه‌بندی‌ها کار را بهینه‌تر کرد، ولی ایده اساسی این الگوریتم به صورتی است که در این مطلب بیان شد. شاخه if-statement اصلی بین دو مورد محور غالب (axis-dominance) بالقوه منشعب می‌شود. کد بالا، octant-aware است و درون دو دامنه if-statement می‌توان مشاهده کرد که کد اساسا بین محورهای X و Y منعکس می‌شود (با متغیرهای px و py دنبال می‌شوند)، اما منطق الگوریتم کاملا مشابه آنچه که پیش‌تر بیان شد است.

فیلم مجموعه آموزش فتوشاپ، طراحی و گرافیک کامپیوتری – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

(pixel(x, y

لازم به یادآوری است که برای نوشتن این کد از canvas یا هیچ نوع کتابخانه گرافیکی دیگری استفاده نشد. این یعنی ابزاری که برای این کار انتخاب می‌شود کاملا بسته به نظر خود کاربر است. تابع (pixel(x, y روشی برای پیاده‌سازی ترسیم یک خط، بسته به نوع صفحه شطرنجی است که مورد استفاده قرار می‌گیرد.

اگر نوشته بالا برای شما مفید بوده، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های پروژه محور برنامه نویسی
• مجموعه آموزش‌های برنامه‌نویسی
• آموزش طراحی وب با HTML – مقدماتی
• آموزش طراحی وب با HTML – تکمیلی
• آموزش پروژه محور HTML و CSS
• مجموعه آموزش‌های طراحی و گرافیک کامپیوتری
• مجموعه آموزش‌های طراحی سه‌بُعدی و متحرک‌سازی