تبدیل اعداد رومی به اعداد صحیح در جاوا اسکریپت — راهنمای کاربردی

فرض کنید از شما خواسته شده است الگوریتمی برای تبدیل اعداد رومی به اعداد صحیح بنویسید. برای توضیح بیشتر به تصویر زیر توجه کنید:

شاید در ابتدا فکر کنید که اگر یک I و پس از آن یک V بیاید، باید آن‌ها را هم کم کنیم. همین طور اگر I و سپس X بیاید آن را نیز کسر می‌کنیم و همین طور تا آخر. اما در این روش باید قواعد بسیار زیادی نوشت. ایده بهتر شاید این باشد که اگر یک رقم رومی با رقم بعدی برابر باشد، می‌توانیم آن را به کل اضافه کنیم. اگر کمتر باشد از بعدی کم می‌کنیم و سپس به نتیجه کلی اضافه می‌کنیم.

اگر هیچ سرنخی از توضیحات فوق به دست نیاوردید، با ما همراه باشید تا به صورت گام به گام در ادامه مسئله را بررسی کنیم.

تجزیه مسئله

ابتدا باید این مسئله را به مسائل کوچک‌تری تقسیم کنیم. به این ترتیب درک می‌کنیم که:

• ارقام منفرد رومی را می‌توان به معادل‌های ده‌دهی‌شان تبدیل کرد.
• قواعدی برای اضافه و کسر تعیین می‌کنیم.
• مجموع را بازگشت می‌دهیم.

فیلم آموزش جاوا اسکریپت JavaScript در فرادرس

کلیک کنید

گام 1: تبدیل اعداد رومی به مقادیر عددی صحیح

در این گام ابتدا I را به 1، V را به 5 و همین طور تا آخر تبدیل می‌کنیم. به این ترتیب لیست بلندی از ثابت‌ها خواهیم داشت:

1const “I” = 1
2const “V” = 5
3etc.

مشکل اینجا است که I یک رشته است و یک متغیر نیست. اگر بخواهید آن را به یک متغیر تبدیل کنید، تعارض زیادی ایجاد می‌شود. ما باید مسائل را تا حد امکان ساده حفظ کنیم. یکی از ساده‌ترین روش‌ها به این منظور به صورت زیر است:

بنابراین کد زیر را می‌نویسیم:

1const romanNumerals = ["M", "D", "C", "L", "X", "V", "I"];
2const integers = [1000, 500, 100, 50, 10, 5, 1];

اگر بخواهیم مقدار III را تست کنیم، ابتدا باید آن I ها را به طور منفرد دربیاوریم. بنابراین رشته را به یک آرایه افراز می‌کنیم:

1let array = s.split('')

و خروجی زیر را به دست می‌آوریم:

1["I", "I", "I"]

()IndexOf

اینک باید هر عنصر آرایه را بررسی کرده و اندیس آن را در آرایه romanNumerals بیابیم. سپس آن را به مقدار عددی ذخیره‌شده در همان اندیس آرایه integers ترجمه می‌کنیم. این کار با استفاده از متد ()IndexOf در جاوا اسکریپت ساده است. بدین ترتیب اگر به دنبال I بگردیم، اندیس آن رشته را می‌توانیم با کد زیر به دست بیاوریم که برابر با 6 است:

romanNumerals.indexOf(“I”)

برای تبدیل به یک مقدار عددی باید صرفاً آن اندیس را در آرایه integers به صورت زیر فراخوانی کنیم:

ntegers[6]

توجه کنید که ما نمی‌خواهیم بدانیم که اندیس برابر با 6 است، بلکه صرفاً می‌خواهیم بدانیم اندیس romanNumeral چیست. بنابراین از کد زیر استفاده می‌کنیم:

integers[romanNumerals.indexOf(“I”)]

که مقدار 1 را به دست می‌دهد. اینک باید این کار را در مورد همه کاراکترهای رشته عدد رومی انجام دهیم.

گام 2: شیوه افزودن مقادیر عددی به مجموع

به جای تعیین قواعدی برای موارد حذف/اضافه مقادیر، ابتدا برنامه‌ای می نویسیم که مقدار هر کاراکتر را به مجموع اضافه کند. کار خود را با کد زیر آغاز می‌کنیم:

1//test value:
2s = "III"
3array = s.split('')
4//set a counter called 'total' with an initial value of zero:
5let total = 0
6       
7for(let i = 0; i < array.length; i++){
8   total += integers[romanNumerals.indexOf(array[i])]  
9 }
10       
11return total
12// => 3

اینک می‌بینیم که تست پاسخ داده است.

گام 3: تعیین زمان و شیوه حذف/اضافه مقادیر

در بخش قبل دیدیم که زمانی یک مقدار به مجموع اضافه می‌شود که بزرگ‌تر از مقدار بعدی باشد و در غیر این صورت از مقدار بعدی کم می‌شود و حاصل به مجموع اضافه می‌شود. بدین ترتیب متدی برای مقایسه مقدار کنونی با مقدار بعدی نوشتیم. اگر عنصر کنونی در آرایه array[i] باشد، در این صورت مقدار بعدی برابر با array[i+1] خواهد بود.

فیلم آموزش JavaScript ES6 جاوا اسکریپت در فرادرس

کلیک کنید

اگر مقدار عددی array[i] برابر با integers[romanNumerals.indexOf(array[i])]، در این صورت array[i+1] برابر با integers[romanNumerals.indexOf(array[i+1])] خواهد بود. بنابراین اگر بخواهیم ببینیم آیا مقدار کنونی بزرگ‌تر یا مساوی مقدار بعدی است، می‌توانیم چیزی مانند زیر بنویسیم:

1if(integers[romanNumerals.indexOf(array[i])] >= integers[romanNumerals.indexOf(array[i+1])] ...
2//feeling dizzy??

کد فوق کمی گیج‌کننده است، بنابراین برای درک بهتر چند متغیر به آن اضافه می‌کنیم:

1let current;
2let currentValue;
3let next;
4let nextValue;
5for (let i=0; i < array.length; i++){        
6    current = array[i];
7    currentValue = (integers[romanNumerals.indexOf(current)]);
8    next = array[i+1];
9    nextValue = (integers[romanNumerals.indexOf(next)]);
10//...

بدین ترتیب نوشتن بخش بعدی راحت‌تر می‌شود:

1if (currentValue >= nextValue ){
2       // add current value to total
3       } else if (currentValue < nextValue) {
4       //subtract current value from next value and add result to total ?
5        }

مشکلی به نام IX

حلقه for طوری تنظیم شده است که هر بار یک عنصر را پردازش کند و در مورد شیوه استفاده از آن برای تغییر مجموع تصمیم‌گیری کند، سپس به سراغ عنصر بعدی می‌رود. اما در بخش elde if کد، با دو عنصر سر و کار داریم که array[i] و array[i+1] هستند.

برای نمونه اگر یک I و سپس X داشته باشیم و I را به 1 و X را به 10 ترجمه کنیم، بر اساس قاعده ما از آنجا که 1 کمتر از 10 است، 1 را از 10 کم می‌کنیم و مقدار 9 به دست می‌آید و 9 را به مجموع اضافه می‌کنیم. اما در حلقه بعدی عنصر کنونی ما همان عنصر «بعدی» قبلی است که برابر با X است و مقدار آن 10 است. اما چنان که دیدیم 10 را قبلاً به مجموع اضافه کرده‌ایم. اگر آن را مجدداً 10 در نظر بگیریم، مجموع به هم می‌خورد.

این وضعیت بغرنجی محسوب می‌شود، چون ما در الگوریتم خود هرگز با دو رقم سر و کار نداشتیم. هر زمان که I جلوی X قرار می‌گرفت یا C جلوی D قرار می‌گرفت، مقدار عددی آن را از مجموع کم می‌کردیم. و سپس مقدار عددی را به حلقه بعدی اضافه می‌نمودیم. اینک چرا باید به روش متفاوتی عمل کنیم؟ چون IX در اعداد رومی به معنی 9 است و بهتر است آن را مانند اعداد صحیح یک عدد در نظر بگیریم تا این که 1 را از 10 کم کنیم.

گام 4: بازگشت مجموع

ما پس از حلقه For، مجموع را بازگشت می‌دهیم. کل تابع اینک به صورت زیر در آمده است:

1const romanToInt = function(s) {
2    const array = s.split('');
3    const romanNumerals = ["M", "D", "C", "L", "X", "V", "I"];
4    const integers = [1000, 500, 100, 50, 10, 5, 1];
5      
6    let total = 0 ; 
7    let current;
8    let currentValue;
9    let next;
10    let nextValue;
11for (let i=0; i < array.length; i++){        
12        current = array[i];
13        currentValue = (integers[romanNumerals.indexOf(current)]);
14        next = array[i+1];
15        nextValue = (integers[romanNumerals.indexOf(next)]);
16if (currentValue >= nextValue ){
17            total += (currentValue);
18        } else if (currentValue < nextValue) {
19            total -= (currentValue);  
20        } else if (currentValue && !nextValue) {
21            total += currentValue
22        }
23        
24    }
25    return total
26}

نتیجه اجرای این الگوریتم به صورت زیر بوده است:

آیا می‌توانیم سرعت الگوریتم را با یک هش افزایش دهیم؟

ما می‌توانیم به جای استفاده از آرایه، اطلاعات اعداد رومی و صحیح را به صورت هش نیز در نظر بگیریم:

1const romanToInt = function(s) {
2    const array = s.split('');
3    
4    const conversion = {"M": 1000, "D":500, "C":100, "L":50, "X":10, "V":5, "I":1}
5    // const romanNumerals = ["M", "D", "C", "L", "X", "V", "I"];
6    // const integers = [1000, 500, 100, 50, 10, 5, 1];
7      
8    let total = 0 ; 
9    let current;
10    let currentValue;
11    let next;
12    let nextValue;
13for (let i=0; i < array.length; i++){        
14        current = array[i];
15        currentValue = conversion[array[i]]
16        // currentValue = (integers[romanNumerals.indexOf(current)]);
17        next = array[i+1];
18        nextValue = conversion[array[i+1]]
19        // nextValue = (integers[romanNumerals.indexOf(next)]);
20if (currentValue >= nextValue ){
21            total += (currentValue);
22        } else if (currentValue < nextValue) {
23            total -= (currentValue);  
24        } else if (currentValue && !nextValue) {
25            total += currentValue
26        }
27        
28    }
29    return total
30}

کد فوق کمی کندتر اجرا می‌شود، گرچه از حافظه کمتری نیز استفاده می‌کند و از این رو رتبه استفاده از حافظه بهبود یافته، اما از نظر رتبه‌بندی سرعت با افت مواجه شده‌ایم:

بهبود عمده الگوریتم

بزرگ‌ترین بهبود این الگوریتم از پاکسازی بخش زیر به دست می‌آید:

1if (currentValue >= nextValue ){
2            total += (currentValue);
3        } else if (currentValue < nextValue) {
4            total -= (currentValue);  
5        } else if (currentValue && !nextValue) {
6            total += currentValue
7        }

این بخش را به صورت زیر بازنویسی می‌کنیم:

1if (currentValue >= nextValue ){
2            total += (currentValue);
3        } else if (currentValue < nextValue) {
4            total -= (currentValue);  
5        }

اما این کد کار نمی‌کند، زیرا یک حالت خاص وجود دارد که در آن currentValue آخرین مقدار در آرایه است. زمانی که این اتفاق بیافتد، هیچ nextValue وجود ندارد که با آن مقایسه کنیم و از این رو کد از ارزیابی آخرین مقدار رد می‌شود. برای اصلاح این مشکل کد زیر را اضافه می‌کنیم:

1else if (currentValue && !nextValue) {
2            total += currentValue
3        }

یعنی اگر مقدار دیگری وجود نداشته باشد، مقدار کنونی به مجموع اضافه خواهد شد.

بهینه‌سازی نهایی

اما این کد نیز موجب کند شدن زیادی در اجرا می‌شود. با بررسی راهکارهای مختلف متوجه می‌شویم که اگر گزاره if را به روش تمیزتر زیر بنویسیم، سرعت اجرایی بهبود عمده‌ای پیدا می‌کند:

1if (currentValue < nextValue ){
2            total -= (currentValue);
3        } else {
4            total += (currentValue);  
5        }

در این حالت مواردی که currentValue آخرین مقدار هست را نیز در نظر گرفته‌ایم. بدین ترتیب کد نهایی به صورت زیر در می‌آید:

1const romanToInt = function(s) {
2    const array = s.split('');
3    const romanNumerals = ["M", "D", "C", "L", "X", "V", "I"];
4    const integers = [1000, 500, 100, 50, 10, 5, 1];
5      
6    let total = 0; 
7    let current;
8    let currentValue;
9    let next;
10    let nextValue;
11    
12    for (let i=0; i < array.length; i++){        
13        current = array[i];
14        currentValue = (integers[romanNumerals.indexOf(current)]);
15        
16        next = array[i+1];
17        nextValue = (integers[romanNumerals.indexOf(next)]);
18        if (currentValue < nextValue ){
19            total -= (currentValue);
20        } else {
21            total += (currentValue);  
22        }
23    return total
24}

این تغییر نهایی تفاوت عمده‌ای در زمان اجرا ایجاد می‌کند:

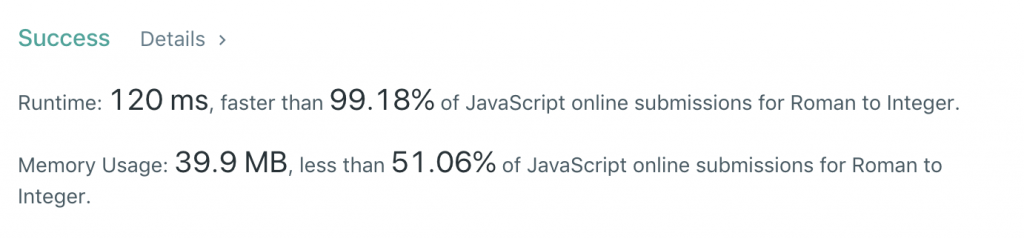
به این ترتیب به پایان این مطلب رسیدیم.

فیلم مجموعه آموزش جاوااسکریپت JavaScript – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های JavaScript (جاوا اسکریپت)
• آموزش جاوا اسکریپت (JavaScript)
• مجموعه آموزش‌های برنامه‌‌نویسی
• شیء (Object) در جاوا اسکریپت — راهنمای کاربردی
• آموزش جاوا اسکریپت مقدماتی: ساخت بازی حدس اعداد — به زبان ساده

==