بررسی شبکه عصبی کانولوشن (CNN) – بخش دوم



در بخش قبل با پرسپترون (Perceptron) به صورت مقدماتی و اولیه آشنا شدیم. حال به ادامه این مبحث می پردازیم:
آموزش پرسپترون
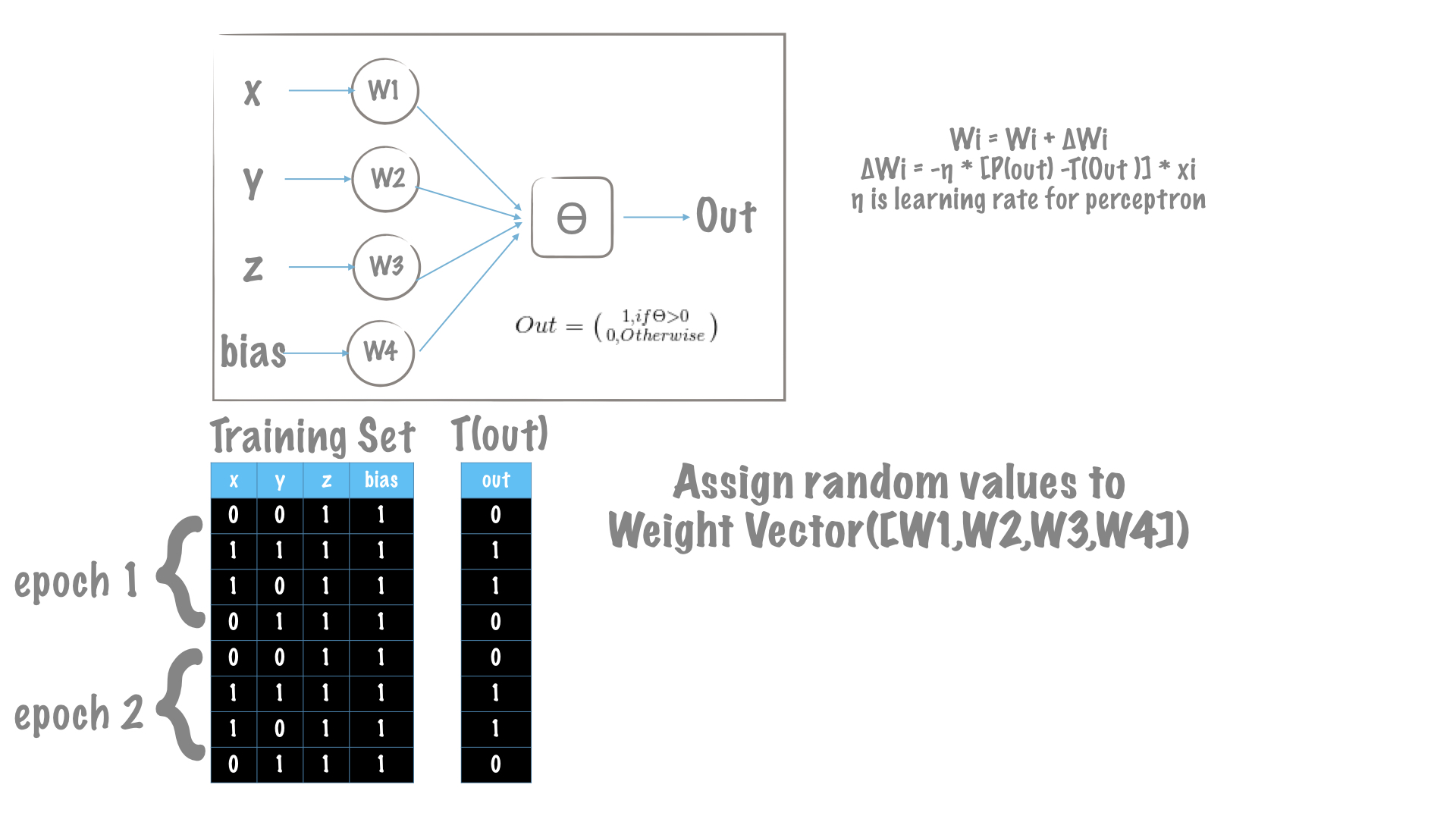
مجموعه داده
ما برای آموزش مدل پرسپترون خود با جدول درستی شروع کردیم.
X: بردار ویژگی برای هر نمونه.
Y: برچسب هر نمونه.
نمایش تصویری فرآیند تغییر وزنها
مقادیر اولیه وزنهای مدل پرسپترون ما، مقادیر تصادفی هستند.
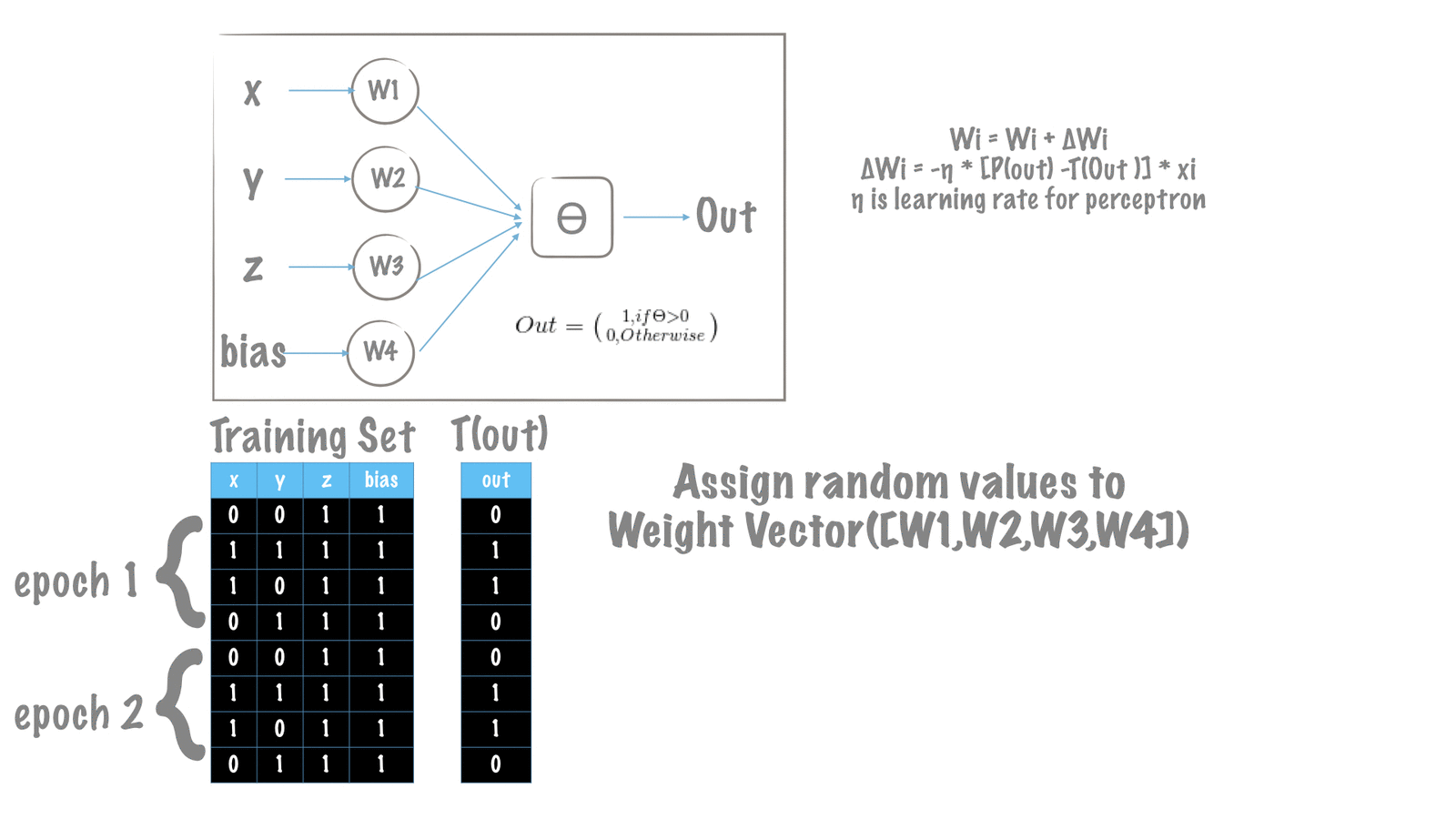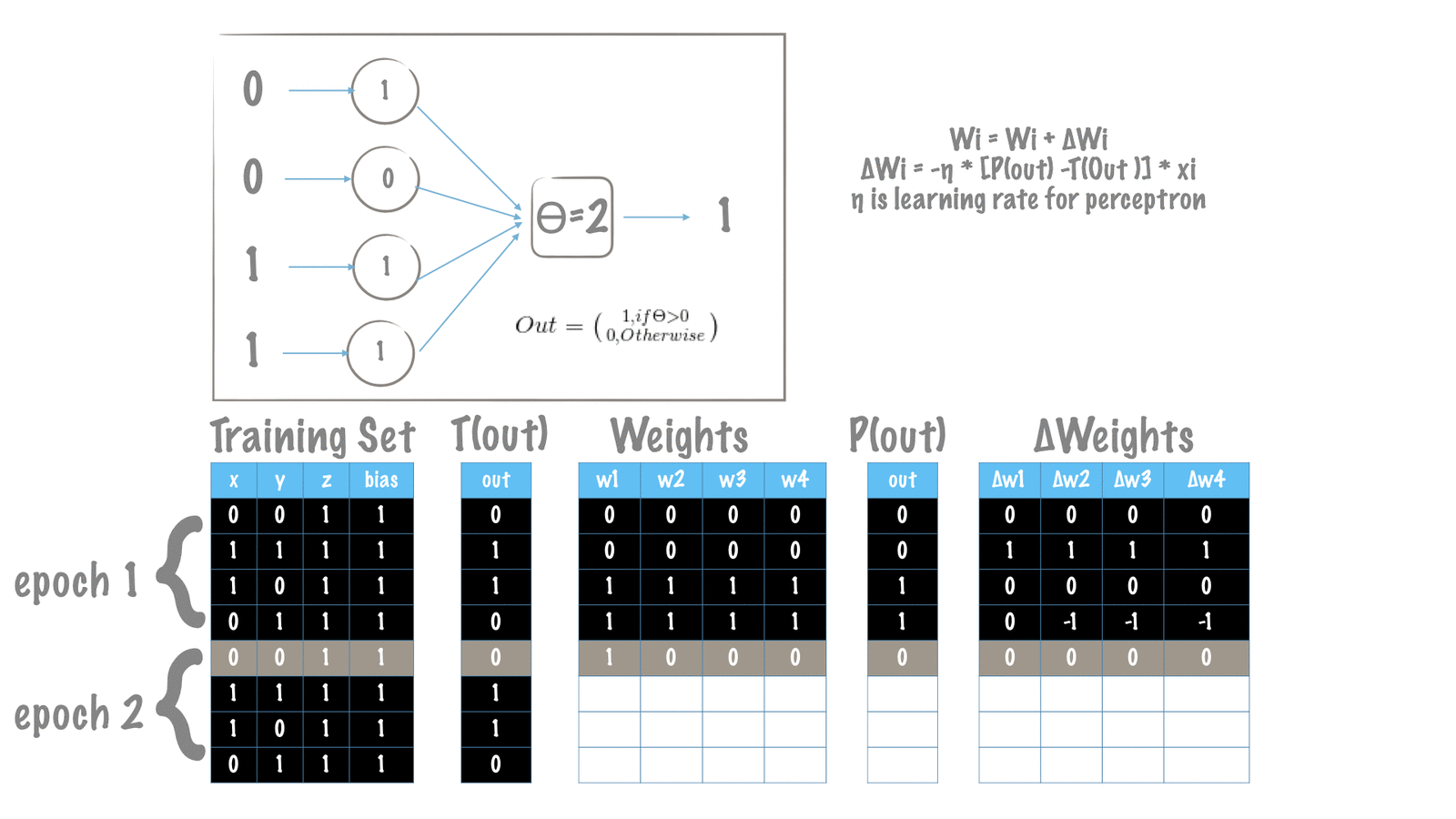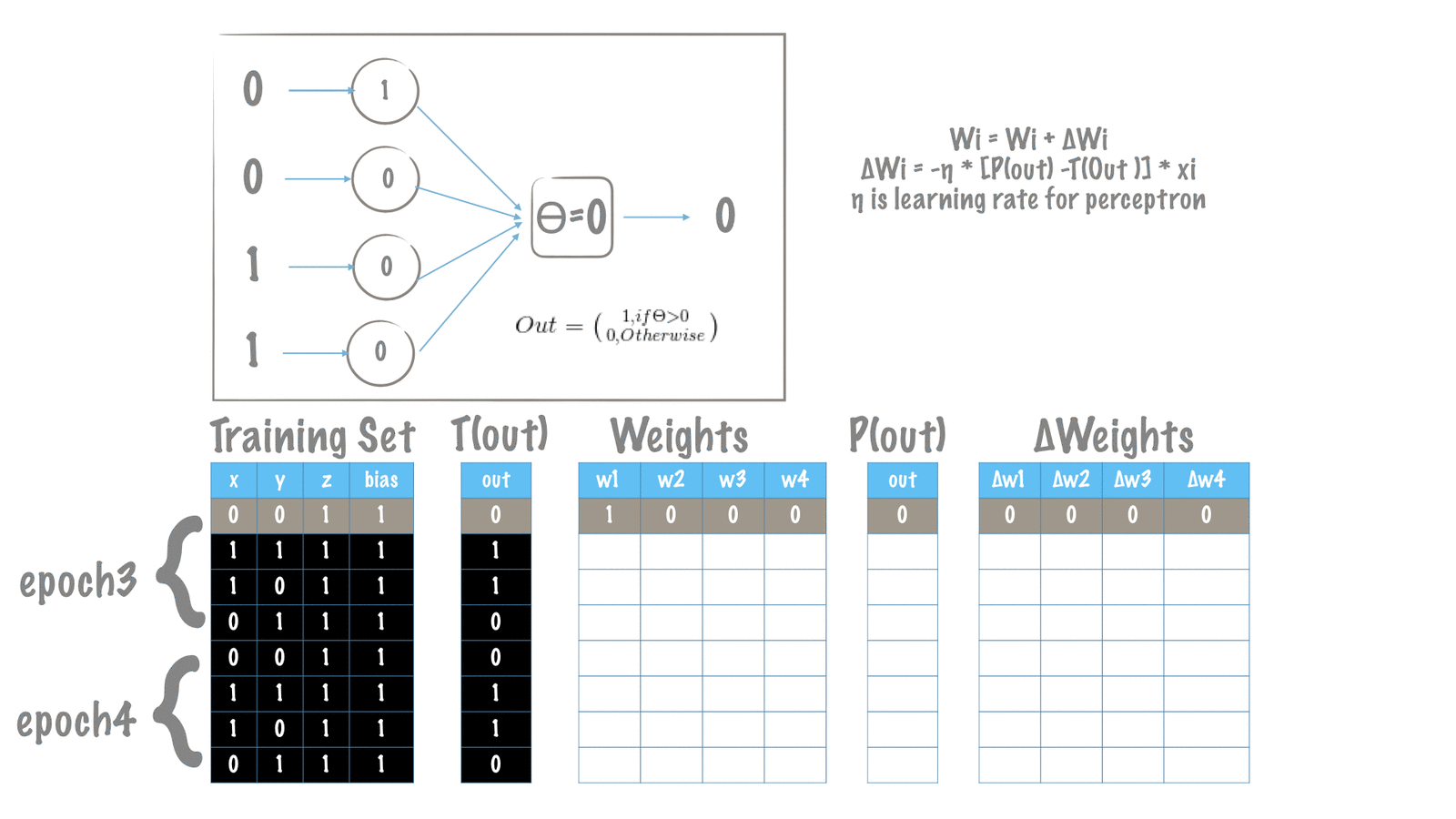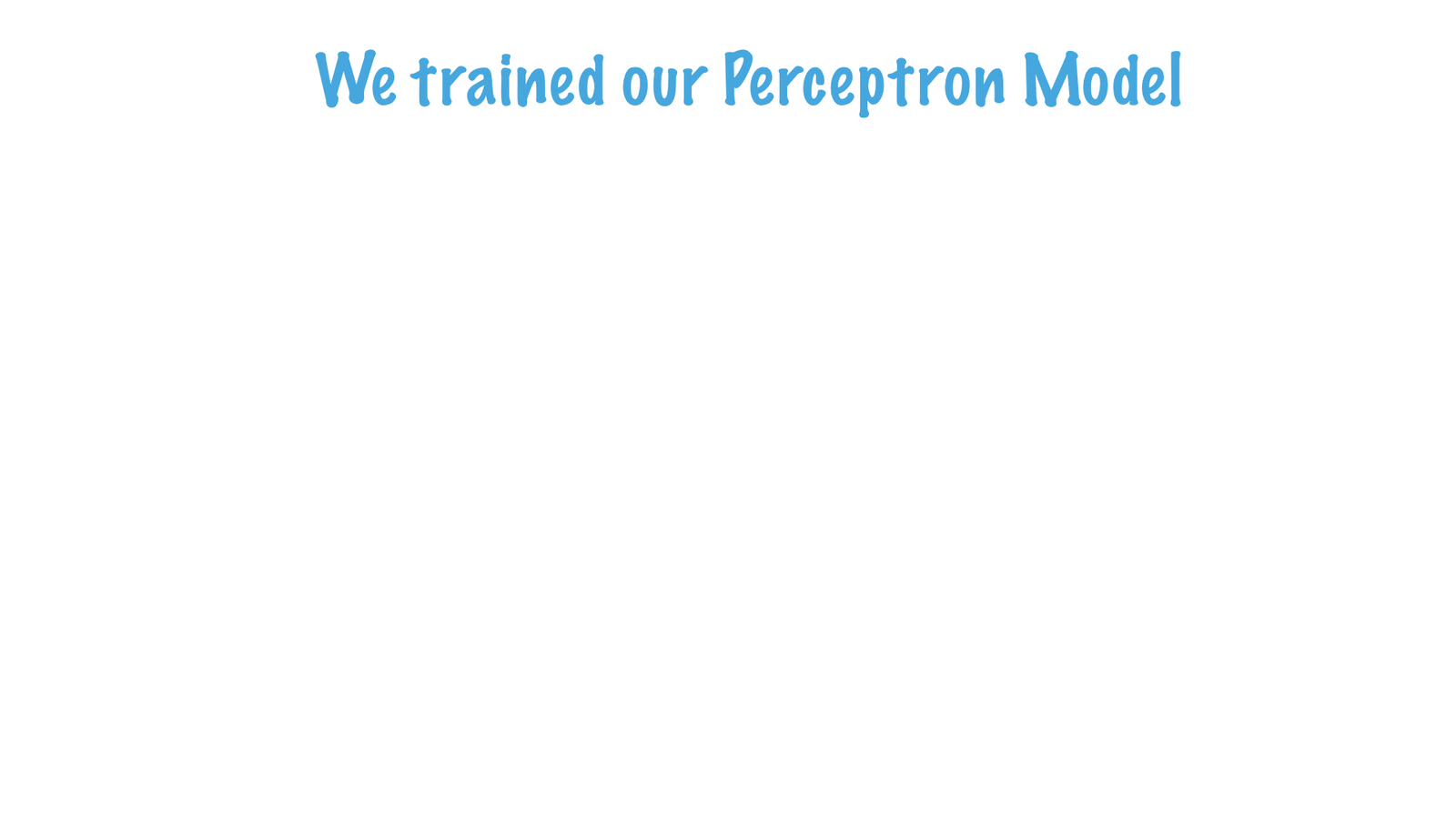
همانطور که در بخش الگوریتم آموزش توضیح داده شد، هدف ما افزایش عملکرد کارهای T است. در هر تکرار، ما پرسپترون را برای پیشبینی خروجی دلخواه در یک جهت و بهصورت پیشرو (feed-forward) حرکت میدهیم. هنگامیکه خروجیها پیشبینی شده (محاسبه شده) با مقادیر مطلوب سازگار نباشد، وزنهای پرسپترون را تغییر میدهیم. تغییر مقادیر وزنها (w) به معنی افزایش یا کاهش وزنها میباشد. این تغییر همان عملی است که در الگوریتم آموزش برای کمینه کردن خطای کلی تعریفشده است.
هنگام بهینهسازی وزنها در آموزش هر مدل، همیشه خطا وجود دارد. نتیجه تابع خطای آموزش معمولی باید مشابه شکل زیر باشد. نرخ یادگیری نمایانگر سرعت آموزش میباشد.
ما در این مقاله، خطا را با خطای مربع تعریف کردهایم. همانطور که در بخش قبل توضیح داده شد، وزنهای دلتا فرمولها را بهصورت زیر تغییر میدهند:
بنابراین، ما هنگام شروع آموزش مدل یک فرا پارامتر (laper-parametr) انتخاب میکنیم. در این مقاله، فرا پارامترها عبارتند از:
چنانچه نرخهای یادگیری متفاوت باشند، ممکن است نقاط خطا نیز متفاوت باشند. اگر نرخ یادگیری بالا باشد، تغییر وزنها بزرگ میباشد و ممکن است آموزش سریعتر باشد.
اگر نرخ یادگیری eta=0.0001 باشد، آموزش تعداد تکرار بیشتری برای حصول کمترین خطا خواهد داشت.

اگر نرخ یادگیری eta=0.01 باشد، سرعت آموزش 10 برابر میشود.

حال که در این مورد اطلاعاتی را کسب کردید، شاید آموزش های زیر بتواند برای شما مفید باشند:
- آموزش یادگیری عمیق (Deep learning)
- مجموعه آموزش های شبکه های عصبی مصنوعی در متلب
- آموزش شبکههای عصبی مصنوعی
**











