روش پسگام – مبانی و مفاهیم

در تئوری کنترل، روش پسگام تکنیکی‌ست که در طی سال‌های 1990 توسط پیتر کوتوویچ و همکارنش برای طراحی کنترل‌های پایدارکننده جهت کلاس خاصی از سیستم‌های پویای غیرخطی توسعه یافته است. این سیستم‌ها از زیرسیستم‌هایی ساخته شده‌اند که از یک زیرسیستم غیر قابل تقلیل که می‌تواند با استفاده از متدهای دیگر پایدار شود، ایجاد می‌شوند. به دلیل وجود این ساختار بازگشتی، طراح می‌تواند فرایند طراحی را از سیستمی که می‌داند پایدار است شروع کند و بعد به کنترل‌کننده‌های جدیدی که هر زیرسیستم بیرونی را پایدار می‌کنند بپردازد (بازگشت به عقب). این فرایند زمانی که به کنترل نهایی برسیم، به پایان می‌رسد. بنابراین، این فرایند را با نام پسگام نامگذاری می‌کنند.

روش پسگام یک متد بازگشتی برای پایدارسازی مبدا یک سیستم در قالب بازخوردی صریح (strict-feedback)، ارائه می‌کند. برای روشن شدن موضوع، سیستمی را در قالب زیر در نظر بگیرید:

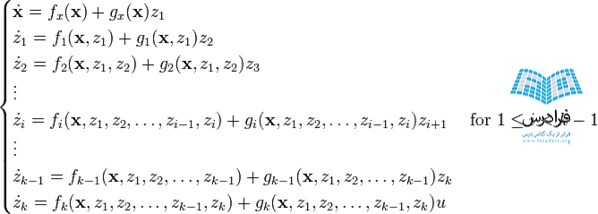
که در آن:

•  .

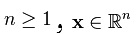•  z₁, z₂, ..., z_i, ..., z_k-1, z_k کمیت‌های نرده‌ای (اسکالر) هستند.

•  u یک ورودی نرده‌ای برای سیستم است.

•  f_x, f₁, f₂, ..., f_i, ..., f_k-1, f_kدر مبدا صفر است (یعنی 0=(0, 0, ..., 0)f_i ).

•   g₁, g₂, ... , g_i, ..., g_k-1, g_kدر دامنه مورد نظر، غیر صفر است (یعن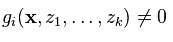ی   برای   ).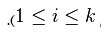

زیرسیستم اول را در نظر بگیرید، یعنی:

فرض کنید این زیرسیستم توسط کنترل مشخص و معلوم  (u_x(x  در مبدا پایدار شده است (یعنی X=0)، به طوریکه  u_x(0)=0 باشد. همچنین فرض می‌شود که یک تابع لیاپونو V_x برای این زیرسیستم پایدار وجود دارد. این بدان معنی‌ست که این زیرسیستم x ، توسط بعضی متدهای دیگر پایدار شده است و متد پسگام پایداری آن را تا شِل z اطراف آن گسترش می‌دهد.

در سیستم‌هایی که در این قالب بازخوردی صریح هستند و یک زیرسیستم پایدار x در آنها وجود دارد، داریم:

•  ورودی کنترلی طراحی شده پسگام، u، بیشترین اثر پایدارای‌ را بر روی حالت دارد.
•  حالت Z_n سپس مانند یک کنترل پایدارکننده بر روی حالت Z_n-1 که حالت قبل از خودش است، عمل می‌کند.
•  این فرایند ادامه می‌یابد تا هر حالت z_i توسط کنترل z_i+1 پایدار شود.

رویکرد پسگام مشخص می‌کند که چگونه زیرسیستم x را با استفاده از z₁ پایدار کرد، و سپس کار را با تعیین اینکه چگونه حالت بعدی یعنی z₂ ، z₁ را به سمت کنترل لازم برای پایدارسازی X پیش برده است، ادامه می‌دهد. بنابراین، این فرایند از x به سمت خارج از سیستم بازخوردی صریح گام برمی‌دارد تا زمانیکه کنترل نهایی u طراحی شود.