حل مسائل خوشه‌بندی با استفاده از الگوریتم کلونی زنبور عسل مصنوعی

در مطلب پیشین، روش حل مسائل بهینه‌سازی جهان واقعی با پیاده‌سازی یک الگوریتم «هوش ازدحامی» (Swarm Intelligence - SI) به نام کلونی زنبور عسل مصنوعی (ABC) ارائه شد.

اکنون زمان آن فرا رسیده تا شیوه استفاده از الگوریتم برای خوشه‌بندی داده‌های واقعی شرح داده شود. در این مطلب نیز از زبان پایتون برای کلیه مراحل پیاده‌سازی استفاده شده است. در ادامه نگاهی عمیق‌تر به مساله خوشه‌بندی داشته و سپس فرآیند پیاده‌سازی الگوریتم کلونی زنبور عسل مصنوعی برای حل این مساله مورد بررسی قرار می‌گیرد.

مساله خوشه‌بندی

مساله خوشه‌بندی یک مساله غیر خوش‌تعریف ان‌پی-سخت (NP-hard) محسوب می‌شود که ایده اصلی آن کشف الگوهای موجود در داده‌ها است. هیچ تعریف رسمی از چیستی خوشه‌بندی وجود ندارد، اما ایده اصلی آن گروه‌بندی عناصر به شیوه‌ای است که بتوان میان آن‌ها در گروه‌های متمایز تفاوت قائل شد.

فیلم آموزش کلونی زنبور مصنوعی Artificial Bee Colony در متلب MATLAB در فرادرس

کلیک کنید

خانواده‌های مختلفی از الگوریتم‌ها برای حل مسائل خوشه‌بندی قابل استفاده هستند که شیوه عملکرد و پیاده‌سازی آن‌ها با یکدیگر متفاوت است. یک راهکار کلاسیک برای تعریف مساله خوشه‌بندی، تبدیل آن به یک مساله ریاضی شناخته شده با عنوان «K-تقسیم‌بندی» (k-partition) از داده‌های اصلی است.

پیدا کردن K-تقسیم‌بندی از مجموعه داده S، به‌صورت K زیر مجموعه از S تعریف می‌شود و از دو قانون زیر تبعیت می‌کند:

• محل تقاطع هر یک از زیر مجموعه‌ها با یکدیگر، برابر با یک مجموعه تهی است.
• اتحاد کلیه زیر مجموعه‌های K برابر با مجموعه S است.

اساسا، در پایان این روال خوشه‌بندی، هدف پیدا کردن زیرمجموعه‌هایی از مجموعه داده اصلی است. از این رو، هیچ نمونه‌ای نمی‌تواند به بیش از یک گروه تعلق داشته باشد. این مفهوم در شکل زیر نمایش داده شده:

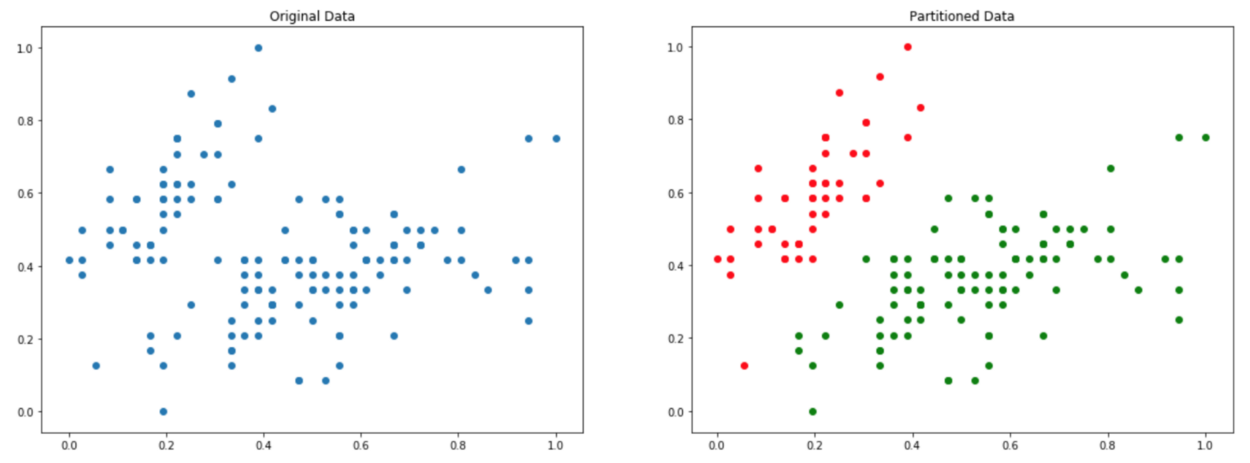
در نمودار، سمت چپ داده‌های اصلی و در سمت راست داده‌های بخش‌بندی شده با K=۲ نمایش داده شده است. K=۲ یعنی در واقع داده‌ها به دو گروه (خوشه) تقسیم شوند.

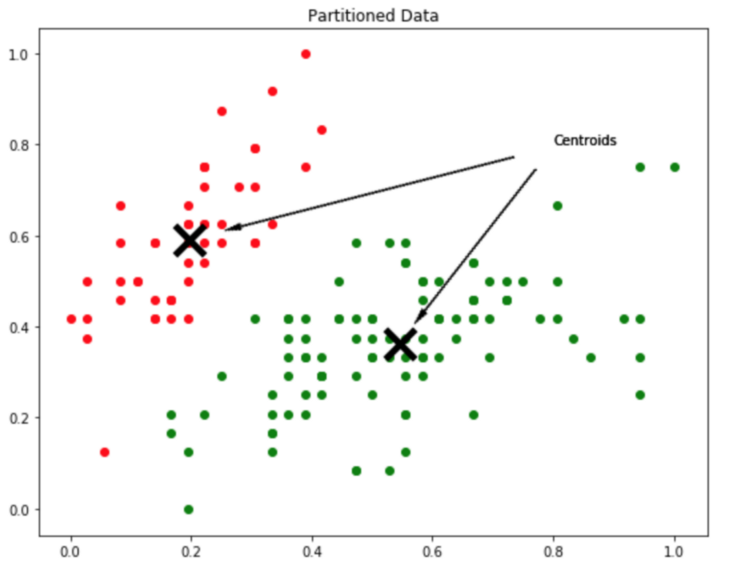
مثالی از چگونگی عملکرد مرکزوارها (centroids) برای بخش‌بندی داده‌ها به دو خوشه (K=۲) در شکل بالا نشان داده شده است.

چگونه می‌توان داده‌ها را برای انجام خوشه‌بندی که در تصویر بالا نمایش داده شده، بخش‌بندی کرد؟ در پاسخ به این سوال باید گفت، خروجی روال خوشه‌بندی مجموعه‌ای از مرکزوارها هستند. مرکزوارها اساسا نمایندگان نمونه داده‌های موجود در هر گروه هستند، بنابراین اگر هدف داشتن K-تقسیم‌بندی از داده‌ها است، باید K مرکزوار وجود داشته باشد.

همچنین، مرکزوارها نقاطی در فضای جست‌و‌جو هستند که توسط داده‌ها تعریف می‌شوند، و از آنجا که هر مرکزوار یک گروه را تعریف می‌کند، هر نقطه داده‌ای به نزدیک‌ترین مرکزوار نسبت به خودش تخصیص داده می‌شود.

اصلاح الگوریتم کلونی زنبور عسل مصنوعی برای خوشه‌بندی

اکنون که چیستی مساله خوشه‌بندی شفاف شد، نیاز به بررسی این امر است که آیا الزامی به اصلاح الگوریتم کلونی زنبور عسل مصنوعی برای انجام فرآیند خوشه‌بندی وجود دارد؟ پاسخی که شاید تعجب‌برانگیز باشد این است، «خیر!»، نیازی به انجام این کار نیست. تنها اقدامی که باید برای اعمال الگوریتم بر مساله خوشه‌بندی انجام داد تبدیل آن به مساله بهینه‌سازی است. چگونگی انجام این کار در ادامه توضیح داده شده است.

فیلم آموزش کلونی زنبور مصنوعی Artificial Bee Colony در متلب MATLAB در فرادرس

کلیک کنید

همانطور که در مطلب پیشین نشان داده شد، یک مساله بهینه‌سازی خوش‌تعریف نیازمند فضای جست‌و‌جو، یک مجموعه داده ورودی از متغیرهای تصمیم d-بُعدی و یک تابع هدف است. اگر به هر یک از زنبورها در کلونی زنبور عسل مصنوعی به‌عنوان یک راهکار کلی برای مساله خوشه‌بندی نگاه شود، هر زنبور عسل مصنوعی می‌تواند یک مجموعه کامل از مرکزوارهای کاندید را ارائه کند. اگر مساله در فضای d-بُعدی، و هدف انجام K-تقسیم‌بندی روی مجموعه داده باشد، هر زنبور یک بردار k.d بعدی است.

اکنون که چگونگی ارائه متغیرهای تصمیم ورودی بیان شد، تنها نیاز به تعریف مرزهای فضای جست‌و‌جو و تابع هدف است. تبیین مرزهای فضای جست‌و‌جو کاری ساده است و با نرمال‌سازی کل مجموعه داده در بازه [۱ و ۰] و تعریف تابع هدف با داشتن مرزهایی از ۰ تا ‍۱ انجام‌پذیر است.

در رویکرد خوشه‌بندی با تقسیم‌بندی، نیاز به بیشینه‌سازی فاصله بین دو گروه متمایز و کمینه‌سازی فاصله خطی درون گروهی است. چندین تابع هدف وجود دارد که در پژوهش‌های این حوزه مورد استفاده قرار می‌گیرد، اما شناخته شده‌ترین آن‌ها مجموع مربعات خطاها (SSE) نامیده می‌شود.

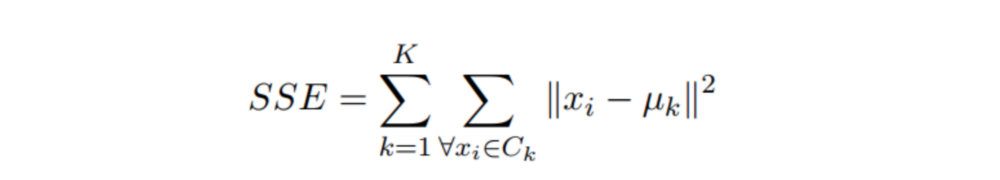
فرمول مجموع مربعات خطاها در بالا نشان داده شده. برخلاف ظاهر پیچیده، مفهوم و شیوه استفاده از آن ساده و قابل درک است.

مجموع مربعات خطاها یک متریک خوشه‌بندی محسوب می‌شود که ایده نفهته در پس آن بسیار ساده است. حاصل این فرمول یک مقدار عددی به حساب می‌آید که مربع فواصل نمونه‌ها تا نزدیک‌ترین مرکز دسته به خودشان را محاسبه می‌کند. هدف از وظیفه بهینه‌سازی، کمینه کردن این تابع است.

می‌توان از چارچوبی که پیش‌تر برای تابع هدف تعریف شد به‌منظور پیاده‌سازی مجموع مربعات خطاها به شکل زیر استفاده کرد:

1@add_metaclass(ABCMeta)
2class PartitionalClusteringObjectiveFunction(ObjectiveFunction):
3
4    def __init__(self, dim, n_clusters, data):
5        super(PartitionalClusteringObjectiveFunction, self)\
6            .__init__('PartitionalClusteringObjectiveFunction', dim, 0.0, 1.0)
7        self.n_clusters = n_clusters
8        self.centroids = {}
9        self.data = data
10
11    def decode(self, x):
12        centroids = x.reshape(self.n_clusters, self.dim)
13        self.centroids = dict(enumerate(centroids))
14
15    @abstractmethod
16    def evaluate(self, x):
17        pass
18     
19class SumOfSquaredErrors(PartitionalClusteringObjectiveFunction):
20
21    def __init__(self, dim, n_clusters, data):
22        super(SumOfSquaredErrors, self).__init__(dim, n_clusters, data)
23        self.name = 'SumOfSquaredErrors'
24
25    def evaluate(self, x):
26        self.decode(x)
27
28        clusters = {key: [] for key in self.centroids.keys()}
29        for instance in self.data:
30            distances = [np.linalg.norm(self.centroids[idx] - instance)
31                         for idx in self.centroids]
32            clusters[np.argmin(distances)].append(instance)
33
34        sum_of_squared_errors = 0.0
35        for idx in self.centroids:
36            distances = [np.linalg.norm(self.centroids[idx] - instance)
37                         for instance in clusters[idx]]
38            sum_of_squared_errors += sum(np.power(distances, 2))
39        return sum_of_squared_errors

اعمال الگوریتم روی داده‌های واقعی

اکنون که مفاهیم الگوریتم کلونی زنبور عسل مصنوعی و چگونگی کارکرد آن، چیستی مساله خوشه‌بندی و چگونگی تبدیل آن به مساله بهینه‌سازی تشریح شد، الگوریتم روی یک مجموعه داده واقعی برای درک هر چه بهتر آن اعمال شده است.

فیلم آموزش کلونی زنبور مصنوعی Artificial Bee Colony در متلب MATLAB در فرادرس

کلیک کنید

در این مطالعه موردی از مجموعه داده معروف Iris استفاده شده. این مجموعه داده چهار بُعدی شامل چهار ویژگی (چهار ستون) از سه گونه گیاه زنبق است. تعداد کل نمونه‌های موجود در مجموعه داده ۱۵۰مورد است. در ادامه، برای بصری‌سازی داده‌ها، یک مجموعه داده دو بُعدی مورد استفاده قرار گرفته. با استفاده از خروجی قطعه کد زیر، می‌توان رابطه بین بُعد دوم و چهارم این مجموعه داده را بررسی کرد.

1import matplotlib.pyplot as plt
2
3from abc import ABC
4from objection_function import SumOfSquaredErrors
5
6from sklearn.datasets import load_iris
7from sklearn.preprocessing import MinMaxScaler
8
9data = MinMaxScaler().fit_transform(load_iris()['data'][:, [1,3]])
10plt.figure(figsize=(9,8))
11plt.scatter(data[:,0], data[:,1], s=50, edgecolor='w', alpha=0.5)
12plt.title('Original Data')

خروجی قطعه کد بالا به شکل زیر است (توزیع داده‌های اصلی را نمایش می‌دهد):

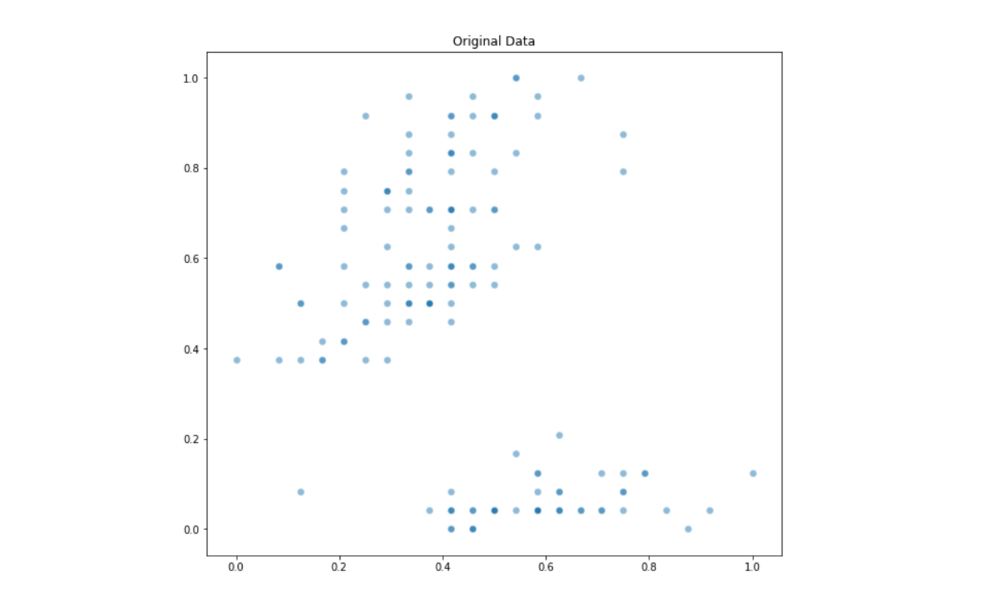
از آنجا که این داده‌ها به عنوان آزمون بنچ‌مارک مورد استفاده قرار می‌گیرند، از هم‌اکنون می‌توان تشخیص داد که تعداد تقسیم‌بندی‌های بهینه برای آن چندتا است و به دلیل وجود داده‌های مربوط به سه گونه زنبق، پس K=۳ است. می‌توان تعداد تقسیم‌بندی‌های بهینه اصلی مجموعه داده Iris را با کد پایتون زیر نمایش داد:

1colors = ['r', 'g', 'y']
2target = load_iris()['target']
3
4plt.figure(figsize=(9,8))
5for instance, tgt in zip(data, target):
6    plt.scatter(instance[0], instance[1], s=50,
7                edgecolor='w', alpha=0.5, color=colors[tgt])
8plt.title('Original Groups')

شکل زیر، خروجی قطعه کد بالا است:

اکنون که مقدار بهینه برای این داده‌های نمونه مشخص است، زمان آن فرا رسیده که از الگوریتم ABC برای حل مساله خوشه‌بندی استفاده کرد. حال از تابع هدف مجموع مربعات خطاها بهره برده و تعداد تقسیم‌بندی‌ها مساوی سه قرار داده می‌شود.

از آنجا که مقداردهی اولیه به صورت تصادفی انجام می‌شود، این احتمال وجود دارد که ترتیب ایجاد شده برای مرکزوارها متناسب با ترتیب کلاس‌ها نباشد. از این‌رو، هنگامی که خروجی‌های الگوریتم ABC روی نمودار نمایش داده می‌شود، ممکن است رنگ گروه‌ها با آن‌ها مطابقت نداشته باشد. این مساله خیلی اهمیت ندارد، مهم‌تر شیوه‌ای است که گروه‌های داده به نظر می‌رسند.

1objective_function = SumOfSquaredErrors(dim=6, n_clusters=3, data=data)
2optimizer = ABC(obj_function=objective_function, colony_size=30,
3                n_iter=300, max_trials=100)
4optimizer.optimize()
5
6def decode_centroids(centroids, n_clusters, data):
7    return centroids.reshape(n_clusters, data.shape[1])
8  
9centroids = dict(enumerate(decode_centroids(optimizer.optimal_solution.pos,
10                                            n_clusters=3, data=data)))
11
12def assign_centroid(centroids, point):
13    distances = [np.linalg.norm(point - centroids[idx]) for idx in centroids]
14    return np.argmin(distances)
15  
16custom_tgt = []
17for instance in data:
18    custom_tgt.append(assign_centroid(centroids, instance))
19
20colors = ['r', 'g', 'y']
21plt.figure(figsize=(9,8))
22for instance, tgt in zip(data, custom_tgt):
23    plt.scatter(instance[0], instance[1], s=50, edgecolor='w',
24                alpha=0.5, color=colors[tgt])
25
26for centroid in centroids:
27    plt.scatter(centroids[centroid][0], centroids[centroid][1],
28                color='k', marker='x', lw=5, s=500)
29plt.title('Partitioned Data found by ABC')

خروجی کد پایتون به شکل زیر نمایش داده می‌شود:

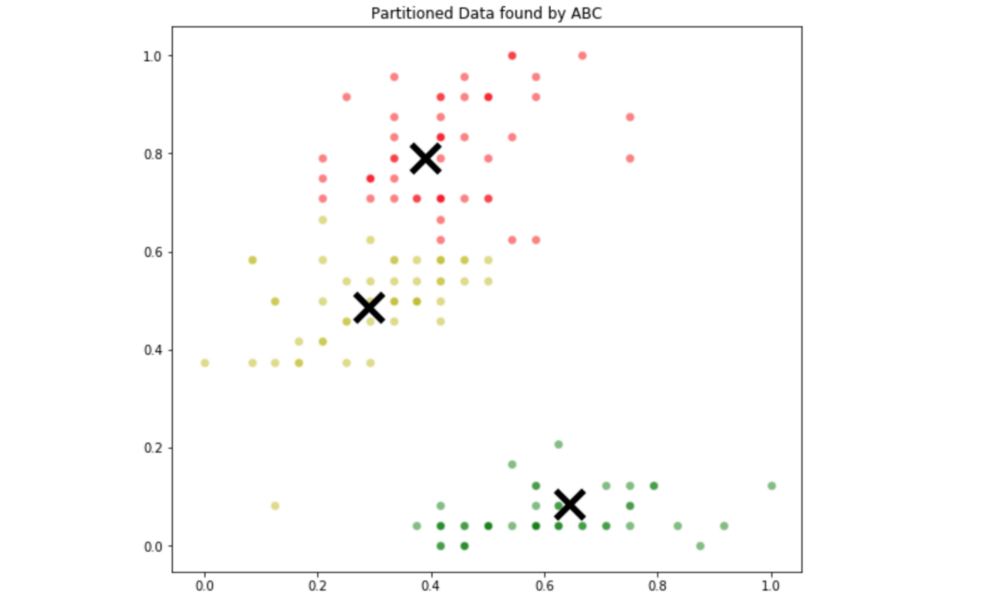
در شکل بالا، خوشه‌های پیدا شده توسط الگوریتم ABC قبل مشاهده هستند. با نگاهی به تقسیم‌بندی اصلی و آنچه توسط الگوریتم ABC ارائه شده، به وضوح می‌توان دید که الگوریتم به خوبی قادر به پیدا کردن خوشه‌هایی نزدیک به مقدار بهینه است. این امر نشان می‌دهد که الگوریتم ABC برای خوشه‌بندی چقدر قدرتمند عمل می‌کند. همچنین، می‌توان چگونگی فرآیند بهینه‌سازی را با نگاهی به خصیصه optimality_tracking مورد بررسی قرار داد.

1itr = range(len(optimizer.optimality_tracking))
2val = optimizer.optimality_tracking
3plt.figure(figsize=(10, 9))
4plt.plot(itr, val)
5plt.title('Sum of Squared Errors')
6plt.ylabel('Fitness')
7plt.xlabel('Iteration')

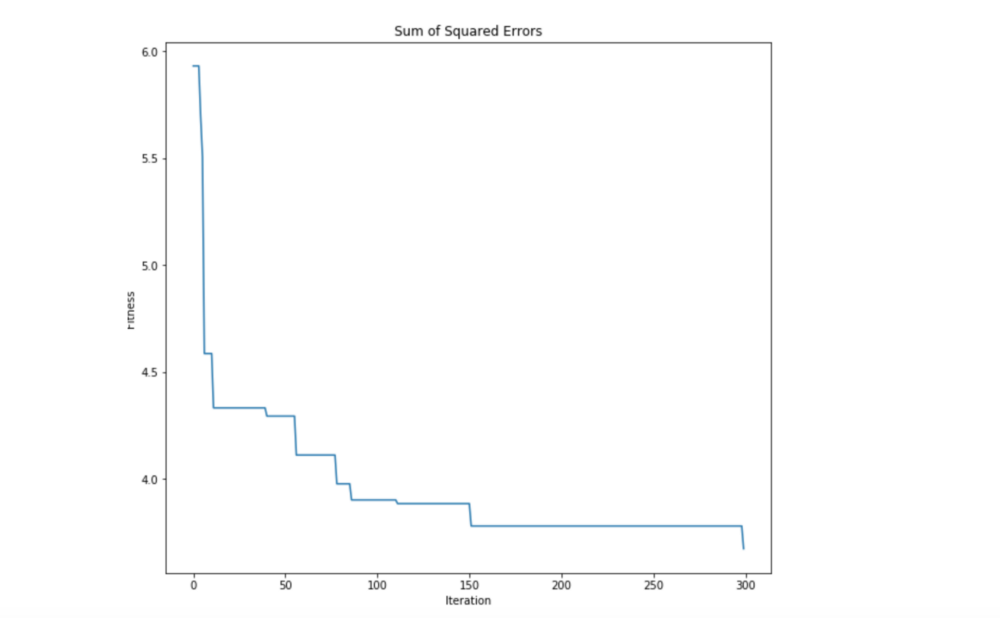
همان‌طور که انتظار می‌رفت، الگوریتم ABC واقعا در کمینه کردن تابع هدف SSE بهینه عمل می‌کند. از این مثال به وضوح قابل مشاهده است که هوش ازدحامی راهکاری قدرتمند برای حل مسائل بهینه‌سازی ارائه می‌کند. این راهکار به خوبی برای حل مسائل جهان واقعی قابل استفاده است و تنها بستگی به این دارد که یک مساله مشخص را چگونه به یک مساله بهینه‌سازی تبدیل کرد.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شود: