تحلیل واریانس (Anova) — مفاهیم و کاربردها

یکی از ابزارهای پرکاربرد در آزمون فرض و تحقیقات آماری، «تحلیل واریانس» (Analysis of Variance) است. در این روش سعی بر این است که اختلاف بین چند جامعه آماری، ارزیابی شود. با توجه به پراکندگی کل داده‌ها، تجزیه واریانس بین گروه‌های مختلف در این روش امکان‌پذیر است. به این ترتیب می‌توان برابر بودن میانگین را بین گروه‌های مختلف آزمود. همچنین در مدل‌های رگرسیونی با تجزیه واریانس کل به واریانس مدل و واریانس خطا تشخیص مناسب بودن مدل قابل ارزیابی است.

برای آگاهی از مفاهیم اولیه آزمون‌های فرض آماری به مطلب تحلیل‌ها و آزمون‌های آماری — مفاهیم و اصطلاحات و برای آشنایی با روش‌های آزمون فرض میانگین به آزمون فرض میانگین جامعه در آمار — به زبان ساده مراجعه کنید. همچنین اطلاع از شیوه محاسبات مربوط به رگرسیون خطی که در مطلب رگرسیون خطی — مفهوم و محاسبات به زبان ساده قابل مطالعه است، خالی از لطف نیست.

تحلیل واریانس (Anova)

تحلیل واریانس و روش‌های تجزیه واریانس، یکی دسته از مدل‌های آماری هستند که قادرند اختلاف بین گروه‌ها یا دسته‌ها را بررسی کنند. این روش توسط «رونالد فیشر» (R. A. Fisher) بیولوژیست و آمارشناس مشهور، ابداع شده است. او در کتاب معروف خود به نام «روش‌های آماری برای محققین» ( Statistical Methods for Research Workers) به بررسی و شیوه تفکیک واریانس پرداخت و به کمک آن بسیاری از آزمون‌های فرض آماری را تشکیل داد.

فیلم آموزش آنالیز واریانس با اس پی اس اس SPSS در فرادرس

کلیک کنید

اساس همه این روش‌ها، تفکیک واریانس یا پراکندگی داده‌ها به چند جزء بود. امروزه کاربرد تحلیل واریانس که با این ایده انجام شده، بسیار زیاد است. در ساده‌ترین شکل، تحلیل واریانس می‌تواند به عنوان یک روش برای آزمون فرض مقایسه میانگین در بین چند جامعه مستقل به کار رود. این کار به عنوان یک جایگزین برای آزمون فرض با استفاده از آماره آزمون T است.

تحلیل واریانس در حالت کلاسیک راه حلی است که سه عمل زیر را همزمان انجام می‌دهد:

1. تجزیه مجموع مربعات کل به مجموع مربعات اجزا حاصل از مدل خطی
2. مقایسه میانگین مربعات، به کمک آماره و آزمون F
3. آزمون پارامترهای مدل به منظور دستیابی به مدل آماری مناسب

شرط‌هایی که باید در هنگام استفاد از تحلیل واریانس در نظر گرفت در لیست زیر قرار گرفته‌اند:

• مقدارهای هر گروه یا جامعه باید دارای توزیع نرمال باشند.
• واریانس در هر گروه ثابت باشد. این امر نشان می‌دهد که نباید داده‌ها شامل «نقاط دورافتاده» (Outlier) باشند.
• واریانس گروه‌ها با یکدیگر برابر باشند.
• میانگین در بین گروه‌ها متفاوت باشد. در حقیقت این همان عبارتی است که به عنوان فرض مقابل در تحلیل واریانس به دنبالش هستیم.

تحلیل واریانس و رگرسیون خطی

در اینجا بهتر است یکی از کاربردهای تحلیل واریانس در رگرسیون را یادآور شویم. اساس کار در تحلیل واریانس، تجزیه واریانس متغیر وابسته به دو بخش است، بخشی از تغییرات یا پراکندگی که توسط مدل رگرسیونی قابل نمایش است و بخشی که توسط جمله خطا تعیین می‌شود. فرض کنید مدل رگرسیونی به صورت زیر داریم:

$$y=\beta_0+\beta_1 X_1+\beta_2X_2+\ldots+\beta_pX_p+e$$

که $$\beta_i$$ پارامترهای مدل و e نیز جمله خطا است. پس در این حالت اگر مجموع مربعات کل را SST، مجموع مربعات خطا را SSE و مجموع مربعات تفاضل مقدارهای برآورد شده از واقعی (پراکندگی داده‌ها مدل) را SSR بنامیم، می‌توان رابطه زیر را نوشت:

SST= SSR+SSE

در صورتی که مدل رگرسیون مناسب باشد،‌ انتظار داریم سهم SSR از SST زیاد باشد، بطوری که بیشتر تغییرات متغیر وابسته توسط مدل رگرسیون توصیف شود. برای محاسبه واریانس از روی هر یک از مجموع مربعات کافی است، حاصل را بر تعداد جملاتشان تقسیم کنیم. به این ترتیب مقدارهای جدیدی به نام‌های «میانگین مربعات خطا» (MSE)،‌ «میانگین مربعات رگرسیون» (MSR) بوجود می‌آیند.

بر همین مبنا و بر اساس این مقدارها، سطرها و ستون‌های جدولی که به جدول تحلیل واریانس (ANOVA) معروف است، ساخته می‌شوند:

در سطر اول که مربوط به مدل رگرسیونی است، «درجه آزادی» (Degree of Freedom) همان تعداد پارامترهای رگرسیون خطی (p) ثبت شده و در سطر مربوط به خطا نیز درجه آزادی n-p-1 در نظر گرفته می‌شود. پس به نظر می‌رسد همان رابطه‌ای که بین مجموع مربعات دیده شد بین درجه آزادی‌های جدول تحلیل واریانس نیز وجود دارد. یعنی:

$$n-1=n-p-1+p$$

از آنجایی که نسبت میانگین مربعات دارای توزیع آماری F است با مراجعه به جدول این توزیع و محاسبه صدک مربوطه، چنانچه متوجه شدیم که مقدار محاسبه شده برای F بزرگتر از مقدار جدول توزیع F با $$p$$‌ و $$n-p-1$$ درجه آزادی در صدک $$1-\alpha$$ام است، پس مدل رگرسیون توانسته بیشتر تغییرات متغیر وابسته را در خود جای دهد در نتیجه مدل مناسبی توسط روش رگرسیونی ارائه شده. در اینجا $$\alpha$$ احتمال خطای نوع اول در نظر گرفته شده است.

تحلیل واریانس و آزمون مقایسه میانگین چند جامعه

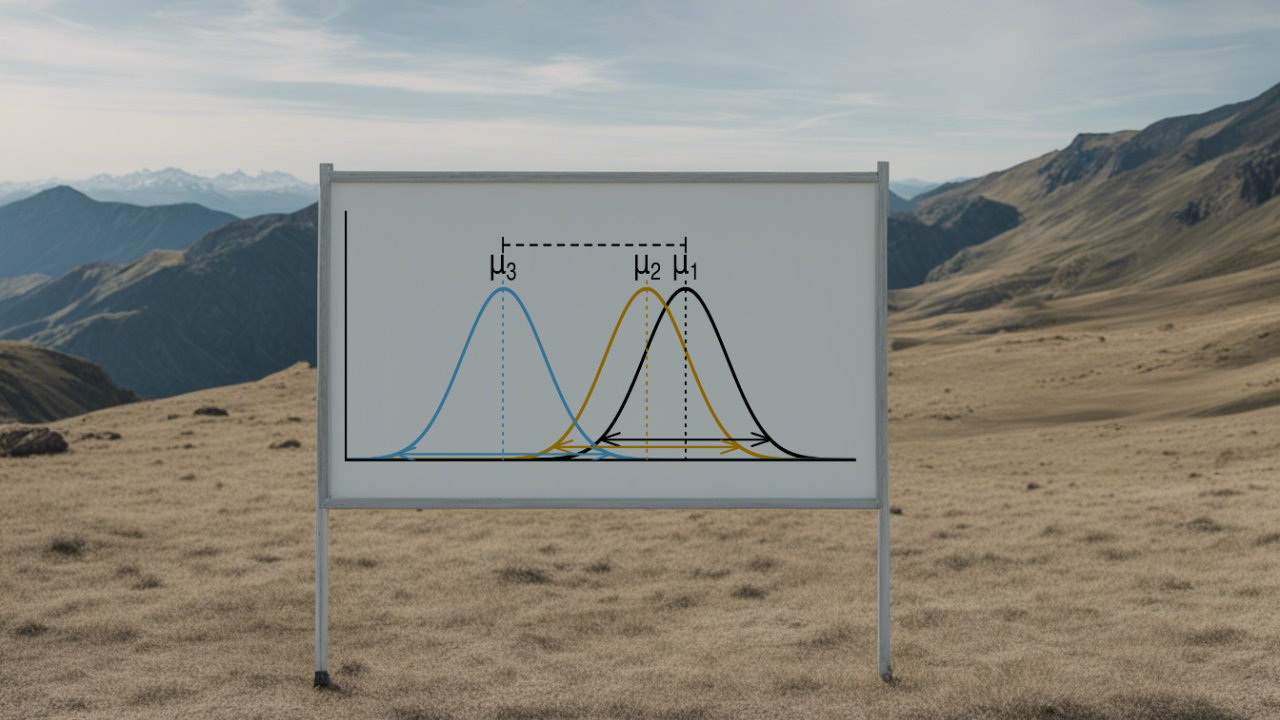
فرض کنید قرار است در مورد یکسان بودن دو یا چند جامعه تحقیق کنید. یکی از شاخص‌های قابل استفاده برای بیان ویژگی‌های جامعه‌ها، می‌تواند میانگین باشد. با مقایسه میانگین و تشخیص برابری یا نابرابر بودن آن‌ها در بین جامعه‌ها، می‌توان رای به یکسان یا متفاوت بودن آن‌ها داد. بنابراین اگر یکی از میانگین‌ها با بقیه تفاوت داشته باشد، متوجه می‌شویم که جوامع مانند یکدیگر نیستند.

فیلم آموزش تجزیه و تحلیل طرح کاملا تصادفی در کشاورزی ‎با SAS‎ (رایگان) در فرادرس

کلیک کنید

با توجه به این موضوع، می‌توان فرضیه‌های آزمون برای مقایسه میانگین k جامعه را به صورت زیر نوشت:

$$\begin{cases} H_0: \mu_1 =\mu_2=\ldots =\mu_k \\ H_1: there\;are\;some\;\mu's\;not\;equal\; with\;others \end{cases}$$

در اینجا فرض مقابل یا $$H_1$$ بیان می‌کند که حداقل یکی از میانگین‌ها با بقیه تفاوت دارد. می‌دانیم که احتمال خطای نوع اول برای مسئله اصلی آزمون به صورت زیر نوشته می‌شود:

$$\alpha_t= P(Error\; Type\; I)=P(Reject\; H_0\;|\;H_0\; is \; true) $$

این عبارت به معنی احتمال رد فرض صفر به شرط صحیح بودن آن است. صحیح بودن فرض صفر بیانگر برابر بودن میانگین‌ها با یکدیگر خواهد بود. برای انجام این بررسی ممکن است از آزمون مقایسه میانگین در بین دو جامعه استفاده کنیم و به صورت ترکیب‌های دوتایی مسئله را تحلیل کنیم. هرچند این کار امکان پذیر است ولی خطای حاصل از انجام چنین آزمون‌هایی از خطای آزمون تحلیل واریانس خیلی بیشتر است. برای نشان دادن این موضوع سه جامعه را در نظر بگیرید.

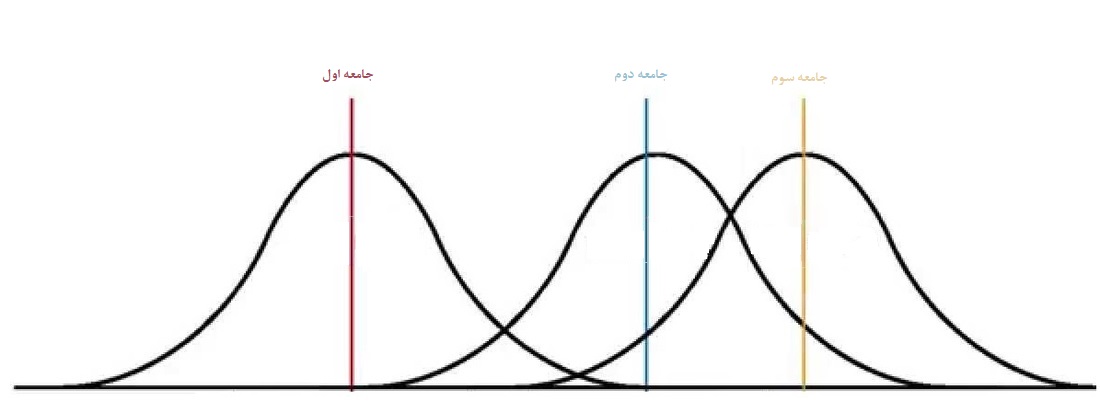
با توجه به ترکیب‌های دو تایی سه میانگین این جوامع، آزمون‌های فرض به صورت زیر درخواهند آمد:

$$1: \begin{cases} H_0: \mu_1 =\mu_2 \\ H_1: \mu_1 \neq \mu_2\\ \end{cases}$$

$$2: \begin{cases} H_0: \mu_1 =\mu_3 \\ H_1: \mu_1 \neq \mu_3\\ \end{cases}$$

$$3: \begin{cases} H_0: \mu_2 =\mu_3 \\ H_1: \mu_2 \neq \mu_3\\ \end{cases}$$

اگر $$A_i$$ را پیشامد «عدم رد فرض صفر آزمون iام با توجه به درست بودن آن» در نظر بگیریم، می‌توان احتمال خطای نوع اول برای هر یک از آزمون‌ها را به صورت زیر محاسبه کنیم.

$$\alpha_i= 1 - P(A_i)$$

حال برای محاسبه احتمال خطای نوع اول همه این آزمون‌ها به طور همزمان، باید احتمال اینکه هیچ‌ یک از $$A_i$$ها رخ ندهد را بدست آوریم. بنابراین اگر $$\cap A_i$$ را پیشامد رخداد همه آن‌ها در نظر بگیریم، کافی است احتمال متمم آن‌ها را محاسبه کنیم.

$$\alpha_t= 1-P(\cap A_i)=1-\prod_{i=1}^k P(A_i))=1-\prod_{i=1}^k(1-\alpha_i)$$

در این حالت اگر احتمال خطای نوع اول را برای همه آزمون‌ها یکسان و برابر با $$\alpha$$ در نظر بگیریم،‌ رابطه بالا ساده‌تر شده و به صورت زیر در خواهد آمد:

$$\alpha_t=1-\prod_{i=1}^k(1-\alpha)=1-(1-\alpha)^k$$

در نتیجه اگر خطای نوع اول برای هر یک از آزمون‌ها $$\alpha=0.05$$ باشد، خطای انجام آزمون همزمان آن‌ها در صورت استفاده از ترکیب‌های دوتایی و انجام آزمون T برابر است با:

$$\alpha_t=1- \prod(1-0.05)=1- (1-0.05)^3=1-(0.95)^3\approx 0.14$$

بنابراین احتمال خطای نوع اول این سه آزمون بسیار بزرگ به نظر می‌رسد. از همین رو این نوع آزمون‌‌ها را نمی‌توان بدون کنترل احتمال خطای نوع اول توسط آزمون‌های T انجام داد. به همین علت استفاده از تحلیل واریانس و جدول ANOVA کار را بسیار ساده می‌کند.

تحلیل واریانس در مسائل مربوط به آزمون میانگین چند جامعه، بر اساس تجزیه «پراکندگی کل» (Total Variation) به «پراکندگی بین‌گروه‌ها» (Variation between groups) و «پراکندگی درون گروه‌ها» (Variation within groups) صورت می‌پذیرد. بنابراین اگر پراکندگی کل را با «مجموع مربعات کل» (Total Sum of Squares- SST)،  پراکندگی بین گروهی را با «مجموع مربعات بین گروه‌ها» (Between Sum of Squares- SSB) و پراکندگی درون گروهی را با «مجموع مربعات درون گروهی» (Within sum of squares- SSW) نشان دهیم، خواهیم داشت:

$$SST=SSB+SSW$$

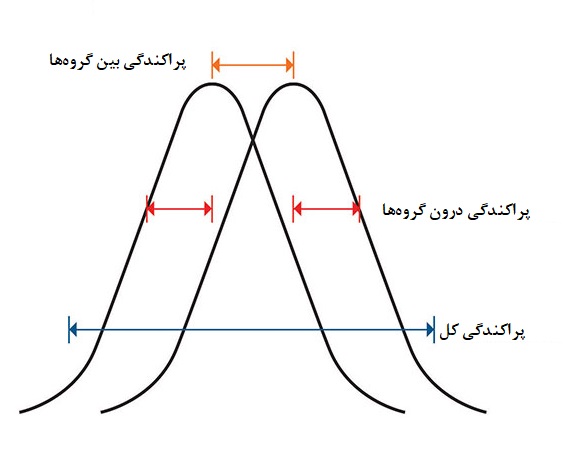
روش محاسبه برای هر یک از اجزای گفته شده نیز به صورت زیر انجام می‌پذیرد:

$$SS_{total}=SST=\sum_{j=1}^k\sum_{i=1}^{n_j}(x_{ij}-\overline{x}\;)^2$$

$$SS_{between}=SSB=\sum_{j=1}^k n_j(\;\overline{x_j}-\overline{x}\;)^2$$

$$SS_{within}=SSW=\sum_{j=1}^k\sum_{i=1}^{n_j}(x_{ij}-\overline{x_j}\;)^2$$

بر این اساس، با توجه به حضور یک متغیر تاثیرگذار در جامعه‌ها، محاسبات مربوط به جدول تحلیل واریانس برای آزمون مقایسه میانگین چند جامعه طبق جدول «تحلیل واریانس یک طرفه» (One Way Anova) انجام می‌شود. در زیر یک نمونه از چنین جدولی قابل رویت است:

در این جدول k تعداد گروه‌ها یا جامعه‌ها و n‌ نیز تعداد مشاهدات است.

متغیری که باعث اختلاف در جامعه‌ها می‌شود را گاهی «عامل» (Factor) نیز می‌نامند. در نتیجه اگر فرض صفر در آزمون فرض میانگین چند جامعه رد شود، می‌توان گفت که متغیر عامل در تغییر میانگین جامعه موثر است.

از ویژگی‌های جدول تحلیل واریانس که آن را به یکی از پرطرفدارترین روش‌های تحلیل آماری بدل کرده، می‌توان به موارد زیر اشاره کرد:

1. شیوه محاسبات آن ساده و قابل درک است.
2. در برابر عدم برقراری فرضیات مربوط به تحلیل،‌ مقاوم است. به این معنی که اگر بعضی از فرضیات مطلوب برای تحلیل واریانس وجود نداشته باشد، باز هم نتایج صحیح از تحلیل بدست می‌آید.
3. تحلیل واریانس یک ابزار قدرتمند در بسیاری از زمینه‌های تحلیل آماری است.
4. در «طرح‌ آزمایش» (Experimental Design) روش مناسب برای استنباط، استفاده از تحلیل واریانس است.

در جدول تحلیل واریانس یک طرفه، یک عامل (یک متغیر)‌ به منظور تفکیک جامعه‌ها وجود داشت. یا به بیان دیگر یک متغیر گروه‌بندی باعث اختلاف در میانگین جامعه‌ها بود. ولی اگر بیش از یک عامل در این تفکیک اثر داشته باشد، مدل تحلیل واریانس پیچیده‌تر شده و حتی اثر عوامل بر یکدیگر را نیز نشان می‌دهد. در نتیجه منابع پراکندگی براساس دو متغیر و همچنین اثر دو متغیر بر یکدیگر تفکیک می‌شوند. در این حالت جدول تحلیل واریانس را دو طرفه (Two way Anova) می‌گویند.

فیلم آموزش تجزیه و تحلیل داده های کشاورزی با نرم افزار MSTAT-C‎ در فرادرس

کلیک کنید

اگر دو متغیر A و B و همچنین اثر هردو تواما روی جامعه‌ها تاثیر گذار بوده و باعث تفکیک آن‌ها شوند، می‌توان ارتباط عوامل و پراکندگی‌ها را به صورت زیر نمایش داد:

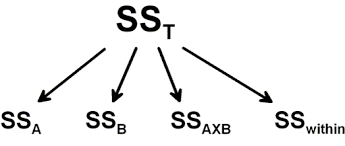
در این حالت $$SS_A$$ پراکندگی در اثر عامل متغیر A‌ از یک طرف، $$SS_B$$ اثر متغیر B از طرف دیگر و همچنین $$SS_{AB}$$‌ پراکندگی توسط هر دو عامل را نشان می‌دهد. همچنین $$SS_{within}$$ نیز بیانگر پراکندگی بین گروه‌ها است.

برای نمونه جدول تحلیل واریانس دو طرفه با در نظر گرفتن اثر متقابل عوامل بر یکدیگر دیده می‌شود.

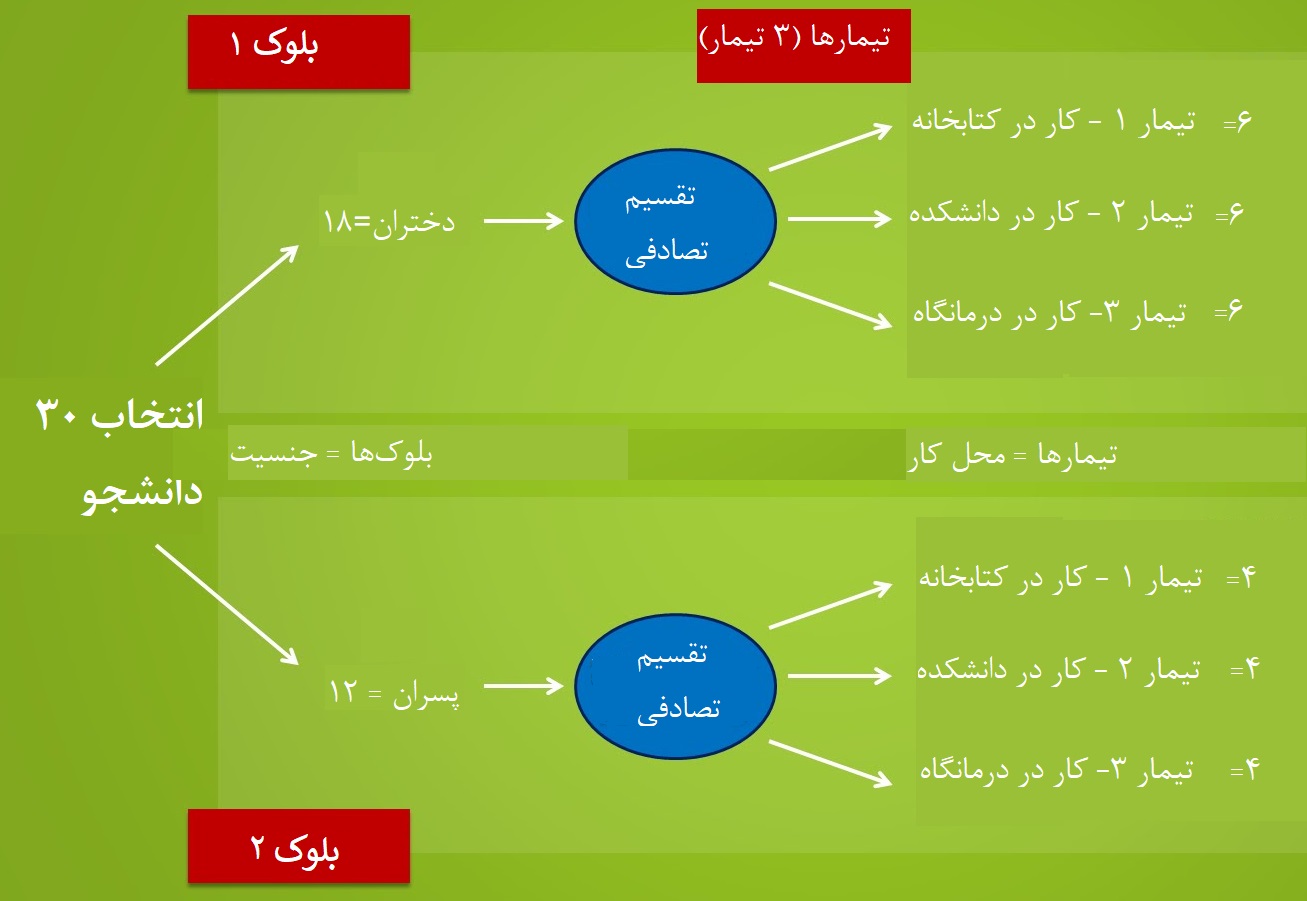
منظور از $$|A|$$ یا $$|B|$$ تعداد سطوح عامل A یا B است. به این معنی که برای مثال اگر عامل جنسیت را متغیر A با دو سطح در نظر بگیریم، $$|A|=2$$ خواهد بود. گاهی اثر عامل A و B‌ را به عنوان «اثرات اصلی» (Main Effect) و اثر هر دو با یکدیگر را «اثر متقابل» (Interaction Effect) می‌نامند.

نکته: گاهی در تحلیل واریانس دو طرفه یا یک طرفه، عامل موثر که توسط محقق قابل کنترل است، تیمار (Treatment) نامیده می‌شود.