درهمسازی (Hashing) در عصر یادگیری ماشین – معرفی جدیدترین تحولات این رشته
در دسامبر 2017 محققان گوگل و MIT یک مقاله تحقیقاتی جنجالبرانگیز در مورد تلاشهایشان در زمینه «ساختارهای اندیس یادگیرنده» منتشر کردند. این تحقیق کاملاً هیجانانگیز بود، چون در بخشی از آن محققان اشاره کردهاند:


«... ما بر این باور هستیم که ایده جایگزینی اجزای اصلی یک سیستم مدیریت داده به وسیله مدلهای یادگیرنده، نتایج بسیار مهمی در طراحی سیستمهای آینده خواهد داشت و این تحقیق تنها گوشه کوچکی از آن چه در آینده ممکن خواهد بود را نشان میدهد.»
در واقع نتایج ارائه شده از سوی محققان تیم گوگل و امآیتی حاوی یافتههایی بوده است که احتمالاً آغاز عصر تازهای از رقابت بین دو پیشکسوت محترم در دنیای اندیسگذاری یعنی درخت بی (B-Tree) و نقشه درهمسازی (Hash Map) خواهد بود. در میان جامعهی مهندسان همیشه در خصوص آینده یادگیری ماشین هیاهو بوده است؛ چنان که انتشار این مقاله تحقیقاتی نیز در سایتهایی نظیر هکر نیوز، ردیت و انجمنهای مهندسی سراسر دنیا غوغا کرده است.
این تحقیق جدید، فرصتی عالی برای آزمون مجدد بنیادهای این رشته فراهم ساخته و چه جالبتر که موضوع آن چیزی است که به اندازه اندیسگذاری بنیادی و کاملاً مطالعه شده محسوب میشود. در این مقاله مقدمهای خواهیم داشت در مورد جدولهای درهمسازی، بررسی مختصری از آن چه بر سرعت آن مؤثر است انجام میدهیم و دیدی شهودی از مفاهیم یادگیری ماشین که در این مقاله در مورد اندیسگذاری به کار گرفته شده است، ارائه میدهیم.
اگر از قبل با جداول درهمسازی، راهبردهای مدیریت تصادم و ملاحظات عملکردی تابع درهمسازی آشنایی دارید، میتوانید از این بخش عبور کرده و به مطالعه ادامه مقاله بپردازید.
اندیسگذاری و یادگیری ماشین
پیتر بِیلیس (Peter Bailis) و تیمی از محققان دانشگاه استنفورد در پاسخ به یافتههای تیم همکاری گوگل و امآیتی، دوباره سراغ اصول اولیه این رشته رفته و از ما خواستهاند که هنوز کتابهای الگوریتم خود را دور نیندازیم. بِیلیس و تیم وی در دانشگاه استنفورد، راهبرد اندیس یادگیرنده را مجدداً خلق کرده و توانستهاند نتایج مشابهی را بدون هیچ گونه یادگیری ماشینی و تنها از طریق راهبرد جدول درهمسازی کلاسیک به نام درهمسازی کوکو (Cuckoo Hashing) به دست آورند.
توماس نئومان در واکنشی مستقل به همکاری گوگل و امآیتی روش دیگری برای رسیدن به عملکردی مشابه راهبرد اندیس یادگیرنده بدون رها کردن الگوریتم درخت B کاملاً آزموده و درک شده، ارائه کرده است. البته این مکالمهها، مقایسهها و درخواست برای تحقیقات بیشتر دقیقاً همان چیزی است که تیم گوگل/امآیتی انتشارش را داشته اند. آنها در مقاله خود اشاره کردهاند:
«لازم است توجه کنیم که ما قصد نداریم ساختارهای اندیس سنتی را به طور کامل با ساختارهای اندیس یادگیرنده جایگزین کنیم. بلکه قصد ما ارائه رویکردی نو برای ساخت اندیس بوده است که در عین تکمیل کردن تحقیقات موجود، مسیری کاملاً جدید برای این شاخه تحقیقاتی که از عمر آن چند دهه می گذرد، بگشاید.»
پس این همه هیاهو بر سر چیست؟ آیا نقشههای درهمسازی و درختهای B محکوم هستند که به موزههای مشاهیر کهن تبدیل شوند؟ آیا ماشینها قصد بازنویسی کتابهای درسی را دارند؟ اگر راهبردهای یادگیری ماشینی واقعاً بهتر از اندیسهای با موضوع عمومی که میشناسیم و عاشقشان هستیم باشند، در این صورت نتیجه این وضعیت در دنیای محاسبات چه خواهد بود؟ اندیسهای یادگیرنده تحت چه شرایطی، عملکردی بالاتر از همتایان قدیمی خود خواهند داشت؟
برای پاسخ به این سؤالها، ابتدا باید درک کنیم که اندیس چیست، چه مشکلاتی را حل میکند و چه چیزی باعث میشود که یک الگوریتم اندیسگذاری بر دیگری ترجیح داده شود.
اندیسگذاری چیست؟
اندیسگذاری در اساسیترین مفهوم خود باعث آسانی یافتن و بازیابی همه چیز میشود. انسان در زمانهایی خیلی قبلتر از اختراع رایانه نیز اندیسگذاری میکرده است. زمانی که از یک کابینت کاملاً مرتب استفاده میکنیم، در واقع مشغول استفاده از سیستم اندیسگذاری هستیم. دائرهالمعارفهای حجیم، خود یک راهبرد اندیسگذاری محسوب میشوند. راهروهای بین قفسهها در یک فروشگاه، نوعی اندیسگذاری هستند. هر زمان که مجموعه بزرگی از اشیا داشته باشیم و بخواهیم شیء خاصی را در میان آنها یافته یا شناسایی کنیم، میتوانیم از یک اندیس برای یافتن آسانتر آن استفاده نماییم.
زنودوتس (Zenodotus) نخستین کتابدار کتابخانه بزرگ اسکندریه مسئول سازماندهی مجموعه بزرگ کتابخانه بود. سیستمی که وی طراحی کرده بود شامل قرار دادن کتابهای مختلف بر حسب موضوع در اتاقهای متفاوت بود و در هر اتاق نیز کتابها بر اساس حروف الفبا مرتب میشد. همتای وی کالیماخوس (Callimachus) از این هم فراتر رفته و یک کاتالوگ مرکزی به نام پیناکس (pinakes) ابداع کرد که به کتابدارها کمک میکرد یک نویسنده را جستجو کرده و بدانند هر کدام از کتابهای آن نویسنده را در کجای کتابخانه میتوان یافت. از آن زمان ابداعات بسیار بیشتری در سیستم اندیسگذاری کتابخانه صورت گرفته است که شامل سیستم ردهبندی دهدهی دیوئی میشود که در سال 1876 ابداع شده است.
در کتابخانه اسکندریه، اندیسگذاری برای نگاشت قطعهای از اطلاعات (نام کتاب یا نویسنده آن) به یک مکان فیزیکی درون کتابخانه استفاده میشد. با این که رایانههای ما ابزارهای دیجیتالی هستند؛ اما باز هم هر نوع دادهای در رایانه دستکم در یک مکان فیزیکی قرار دارد. این دادهها میتوانند متن این مقاله، سوابق جدیدترین تراکنش کارت اعتباری یا ویدئویی بامزه از یک گربه ترسیده باشند. در هر صورت دادهها در یک مکان فیزیکی روی رایانه ذخیره شدهاند.
در RAM و درایوهای حالتجامد (SSD) دادهها به صورت ولتاژ الکتریکی که از میان یک سری از ترانزیستورهای زیاد عبور میکنند، ذخیره میشوند. در هارد درایوهای چرخشی قدیمیتر، دادهها در قالب مغناطیسی بر روی قطاع خاصی از دیسک ذخیره میشدند. زمانی که میخواهیم اطلاعات را در رایانه اندیسگذاری کنیم، نقشههای درهمسازی ایجاد میکنیم که بخشی از دادهها را در موقعیت فیزیکی درون رایانهمان نگاشت میکند. ما این مکان را آدرس مینامیم. در رایانهها همه چیز همواره به صورت بیت (bit)های دادهای اندیسگذاری میشود و از اندیسها برای نگاشت این دادهها به آدرسهایشان استفاده میشوند.
پایگاههای داده از مهمترین استفادههای اندیسگذاری محسوب میشوند. پایگاههای داده برای این طراحی شدهاند که اطلاعات زیادی را در خود جای دهند و به بیان کلیتر ما میخواهیم این اطلاعات را به طرز مؤثرتری بازیابی کنیم. موتورهای جستجو در هسته مرکزی خود اندیسکنندههای عظیمی برای اطلاعات موجود روی اینترنت هستند. جداول درهمسازی، درختهای جستجوی دودویی، درختهای B و فیلترهای بلوم همگی نوعی از اندیسگذاری محسوب میشوند.
چالشهای یافتن چیزهای مختلف در سالنهای تودرتوی کتابخانه شلوغ اسکندریه به خوبی قابل تصور است؛ اما هرگز نمیتوانستیم تصور کنیم که حجم دادههای تولید شده از سوی انسان، چنین رشد نمایی داشته باشد. مقدار دادههایی که روی اینترنت در دسترس است، بسیار بیشتر از حجم هر نوع کتابخانهای در هر زمان است و هدف گوگل این است که همه آن را اندیسگذاری کند. بشر تاکتیکهای مختلفی برای اندیسگذاری ابداع کرده است، در این نوشته ما یکی از قدرتمندترین ساختارهای دادهای در همه زمانها که از قضا یک ساختار اندیسگذاری است را بررسی میکنیم. این ساختار، جدول درهمسازی است.
جدول درهمسازی چیست؟
جداول درهمسازی در سادهترین صورت خود ساختارهای دادهای سادهای بر مبنای چیزی هستند که تابع درهمسازی نامیده میشوند. انواع مختلفی از تابعهای درهمسازی وجود دارند که به طرز اندکی متفاوت عمل میکنند و به منظورهای مختلفی طراحی شدهاند. در بخش بعدی این نوشته تنها تابعهای درهمسازی که در جدول درهمسازی استفاده میشوند را بررسی میکنیم و نه تابعهای درهمسازی رمزنگاری، بررسی مجموعها (checksum) یا هر نوع تابع درهمسازی دیگر.
هر تابع درهمسازی، یک مقدار ورودی میپذیرد که میتواند عدد یا متن باشد و یک مقدار صحیح باز میگرداند که کد درهمسازی یا مقدار درهمسازی نامیده میشود. برای هر ورودی مفروض، کد درهمسازی همواره مقدار یکسانی است. این بدان معنی است که تابع درهمسازی باید تعیینپذیر (deterministic) باشد.
زمانی که یک جدول درهمسازی ایجاد میکنیم در ابتدا مقداری فضا روی حافظه یا دیسک به آن اختصاص میدهیم. مثلاً میتوانید فرض کنید که آرایهای با اندازه دلخواه ایجاد میکنیم. اگر دادههای زیادی داشته باشیم باید از آرایه بزرگتری استفاده کنیم. اگر دادههای کمتری داشته باشیم از آرایه کوچکتری استفاده میکنیم. هر زمان که بخواهیم قطعهای منفرد از دادهها را اندیسگذاری کنیم یک جفت کلید/مقدار میسازیم که در آن کلید، نوعی اطلاعات شناسایی در مورد دادهها، مثلاً کلید ابتدایی رکورد پایگاه داده و مقدار نیز خود داده یعنی برای مثال، کل رکورد پایگاه داده است.
برای درج مقداری در یک جدول درهمسازی کلیدی را به دادههای خود میفرستیم تا تابع را درهمسازی کند. تابع درهمسازی یک مقدار صحیح (کد درهمسازی) باز میگرداند و ما از این مقدار صحیح که هم پیمانه اندازه آرایه است، به عنوان اندیس ذخیرهسازی برای مقدار درون آرایهمان استفاده میکنیم. اگر بخواهیم مقداری را از جدول درهمسازی بیرون بیاوریم، کافی است به سادگی کد درهمسازی را از روی کلید مجدداً محاسبه کنیم و دادهها را از موقعیت آرایه بازیابی نماییم. این موقعیت آدرس فیزیکی دادهها است.
در یک کتابخانه که از سیستم دهدهی دیوئی استفاده میکند، مفهوم «کلید» یک سری از طبقهبندیهای مربوط به کتاب و «مقدار» خود کتاب است. در این سیستم «کد درهمسازی» مقدار عددی است که با استفاده از فرایند دهدهی دیوئی میسازیم. برای مثال یک کتاب در مورد هندسه تحلیلی دارای کد درهمسازی به صورت 516.3 است. کد علوم طبیعی 500، ریاضیات 510، هندسه 516 و هندسه تحلیلی 516.3 است. بدین ترتیب سیستم دهدهی دیوئی را میتوان یک تابع درهمسازی برای کتابها در نظر گرفت. سپس کتابها بسته به مقادیر درهمسازیشان در یک مجموعه از قفسهها قرار میگیرند و درون قفسه خاص خود بر اساس نام نویسنده به طور الفبایی مرتب میشوند.
البته این مقایسه چندان کامل نیست، چون یک مقدار درهمسازی که برای اندیسگذاری جدول درهمسازی استفاده میشود برخلاف اعداد دهدهی دیوئی، اطلاعاتی به دست نمیدهد. در یک استعاره کامل، کاتالوگ کتابخانه باید شامل مکان دقیق هر کتاب بر اساس اطلاعاتی از قبیل عنوان، نام خانوادگی نویسنده، شماره شابک و ... باشد، اما خود کتابها به هیچ روش معنیداری گروهبندی یا مرتب نمیشوند؛ به جز این که کتابهای دارای کلید مشترک در یک قفسه هستند و میتوانید شماره قفسه را با استفاده از کلید مربوطه در کاتالوگ کتابخانه جستجو کنید.
این فرایند ساده به طور بنیادی همه آن کاری است که یک جدول درهمسازی انجام میدهد. با این حال پیچیدگی بسیار زیادی در پس همین ایده ساده نهفته است تا درستی و کارایی اندیسهای مبتنی بر درهمسازی تضمین شود.
ملاحظات عملکردی اندیسهای مبتنی بر درهمسازی
منبع اصلی پیچیدگی و بهینهسازی در جدول درهمسازی، از مسئله تصادم درهمسازی ناشی میشود. تصادم زمانی رخ میدهد که دو یا چند کلید، کد درهمسازی یکسانی را تولید کنند. برای مثال تابع درهمسازی ساده زیر را در نظر بگیرید که در آن کلید به صورت عدد صحیح فرض شده است:
function hashFunction(key) {
return (key * 13) % sizeOfArray;
}
یک تابع درهمسازی ساده
با این که هر عدد صحیحی وقتی در عدد 13 ضرب شود، نتیجه منحصربهفردی ایجاد میکند؛ اما کد درهمسازی حاصل به دلیل اصل لانه کبوتری همچنان در نهایت تکرار خواهد شد. طبق اصل لانه کبوتری نمیتوان 6 چیز مختلف را در 5 سطل قرار داد، مگر اینکه دو آیتم در یک سطل قرار گرفته باشند. از آنجا که مقدار حافظه ما محدود است، باید از پیمانه مقدار درهمسازی نسبت به اندازه آرایه استفاده کنیم و بدین ترتیب همواره احتمال تصادم وجود دارد.
کمی بعدتر در مورد راهبردهای رایج برای مدیریت این تصادمهای ناگزیر بحث میکنیم؛ اما نخست باید اشاره کنیم که انتخاب تابع درهمسازی میتواند بر نرخ وقوع تصادم تأثیر بگذارد. فرض کنید در مجموع 16 موقعیت ذخیرهسازی داریم و باید بین دو تابع درهمسازی زیر یکی را انتخاب کنیم:
function hash_a(key) {
return (13 * key) % 16;
}
function hash_b(key){
return (4 * key) % 16;
}
شما کدام یک را انتخاب میکردید؟
در این مورد اگر بخواهیم اعداد بین 0 تا 23 را درهمسازی کنیم، تابع hash_b میتواند 28 تصادم ایجاد کند؛ 7 تصادم برای هر یک از مقادیر 0، 4، 8 و 12. در واقع چهار درج نخست تصادمی ایجاد نمیکنند؛ اما درجهای بعدی همگی تصادم ایجاد خواهند کرد. با این حال تابع hash_a میتواند توزیع یکنواختی از تصادمها به دست بدهد که برای هر اندیس یک تصادم و در مجموع 16 تصادم وجود خواهد داشت. دلیل این امر آن است که در hash_b عددی که داریم در 4 که فاکتور اندازه جدول درهمسازی است، ضرب میشود (16). از آنجا که عدد اولی (prime number) را در تابع hash_a انتخاب کردهایم، به جز در حالتی که اندازه حجم، مضربی از 13 باشد، مشکل گروهبندی که در تابع hash_b را نخواهیم داشت.
برای دیدن این حالت میتوانید اسکریپت زیر را اجرا کنید:
function hash_a(key) {
return (13 * key) % 16;
}
function hash_b(key){
return (4 * key) % 16;
}
let table_a = Array(16).fill(0);
let table_b = Array(16).fill(0);
for(let i = 0; i < 32; i++) {
let hash_code_a = hash_a(i);
let hash_code_b = hash_b(i);
table_a[hash_code_a] += 1;
table_b[hash_code_b] += 1;
}
console.log(table_a); // [2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2]
console.log(table_b); // [8,0,0,0,8,0,0,0,8,0,0,0,8,0,0,0]
تابعهای درهمسازی بهتر، تصادمها را به صورت یکنواختتری روی جدول توزیع میکنند.
این راهبرد درهمسازی یعنی ضرب کردن کلید ورودی در یک عدد اول، در عمل نسبتاً رایج است. عدد اول احتمال این که کد درهمسازی خروجی، عامل مشترکی با اندازه آرایه داشته باشد و بدین ترتیب احتمال تصادم را کاهش میدهد. از آنجا که جدولهای درهمسازی مدت زیادی است که استفاده میشوند، تابعهای درهمسازی رقیب زیادی نیز برای انتخاب کردن وجود دارند.
درهمسازی ضربی-جابجایی (Multiply-shift) همانند راهبرد پیمانه عدد اول است که معرفی کردیم. اما در این روش به جای عملیات نسبتاً پر هزینه پیمانه، از عملیات جابجایی استفاده میشود که بسیار سریعتر است. MurmurHash و درهمسازی Tabulation نیز جایگزینهای قدرتمندی برای خانواده ضربی-جابجایی تابعهای درهمسازی هستند. مقایسه عملکرد این تابعهای درهمسازی شامل بررسی سرعت محاسبه آنها، توزیع کدهای درهمسازی تولید شده و انعطافپذیری آنها در مدیریت انواع مختلفی از دادهها، برای مثال رشتهها و اعداد اعشاری علاوه بر اعداد صحیح است. برای مشاهده نمونهای از این مقایسهها میتوانید به این آدرس مراجعه کنید.
اگر تابع درهمسازی مناسبی انتخاب شود، هم میتوان نرخ تصادم را کاهش داد و هم کد درهمسازی را همچنان به طرز سریعی تولید کرد. متأسفانه صرفنظر از این که کدام تابع درهمسازی را انتخاب کنیم، در نهایت با تصادم مواجه خواهیم شد. تصمیمگیری در مورد نحوه مدیریت تصادمها تأثیر مهمی بر عملکرد کلی جدول درهمسازی ما خواهد داشت. دو راهبرد عمده برای مدیریت تصادم، زنجیرهسازی (chaining) و کاوش خطی (linear probing) هستند.
زنجیرهسازی سرراست و پیادهسازی آن آسان است. به جای این که یک آیتم منفرد در هر اندیس جدول درهمسازی ذخیره شود، اشارهگر اصلی به یک فهرست لینک شده ذخیره میشود. هر زمان که یک آیتم در تابع درهمسازی ما با اندیس قبلاً پرشدهای تصادم داشت، آن را به صورت یک عنصر نهایی به فهرست لینک شده اضافه میکنیم. بدین ترتیب جستجوها دیگر به طور کامل «زمان ثابت» ندارند، چون باید یک فهرست لینک شده را نیز برای یافتن یک آیتم خاص پیمایش کنیم. اگر تابع درهمسازیمان تصادمهای زیادی ایجاد کند، زنجیرههای طولانی خواهیم داشت و عملکرد جدول درهمسازی در طی زمان به دلیل جستجوهای طولانیتر کاهش مییابد.

زنجیرهسازی: تصادمهای مکرر، فهرستهای لینک شده طویلتری میسازند؛ اما اندیسهای اضافی دیگری از آرایه را اشغال نمیکنند.
کاوش خطی گرچه مفهوم سادهتری دارد؛ اما پیادهسازی آن دشوارتر است. در رویکرد کاوش خطی، هر اندیس در جدول درهمسازی همچنان برای ارائه یک آیتم منفرد ذخیره میشود. وقتی تصادمی در مثلاً اندیس i رخ میدهد، بررسی میکنیم که آیا اندیس i+1 خالی است یا نه و اگر چنین بود دادهها را در آنجا ذخیره میکنیم؛ اما اگر i+1 خالی نبود، i+2 را بررسی میکنیم و سپس i+3 و همینطور تا زمانی که یک اندیس خالی پیدا کنیم. در این حالت هم جستجوها ممکن است از لحاظ زمانی کاملاً ثابت نباشند؛ اگر چند تصادم در این اندیس وجود داشته باشند، مجبور هستیم فهرست طویلی از آیتمها را پیش از یافتن آیتمی که به دنبالش هستیم بگردیم. اشکال دیگر این است که هر زمان با تصادمی مواجه شدیم، احتمال وقوع تصادمهای بعدی را افزایش میدهیم، چون بر خلاف روش زنجیرهسازی، آیتم ورودی در نهایت اندیس جدیدی را اشغال میکند.

کاوش خطی: با فرض یکسان بودن دادهها و تابعهای درهمسازی همانند تصویر فوق، نتیجه جدیدی دریافت خواهیم کرد. اجزایی که یک تصادم ایجاد میکنند (با رنگ قرمز) اینک در همان آرایه قرار میگیرند و اندیسهایی را اشغال میکنند که متعاقباً خود باعث وقوع تصادم میشوند.
ممکن است به نظر برسد که زنجیرهسازی گزینه بهتری است؛ اما کاوش خطی به دلیل داشتن شاخصههای عملکردی بهتر، پذیرش عمومی بیشتری داشته است. در اغلب موارد، این امر به دلیل کاربرد کمتر کش کردن برای فهرستهای لینک شده است و این که استفاده از کش در آرایهها بهتر عمل میکند. به بیان کوتاهتر، بررسی همه لینکها در یک فهرست لینک شده بسیار کندتر از بررسی همه اندیسهای یک آرایه با همان اندازه است. دلیل این مسئله آن است که هر اندیس از نظر فیزیکی در مجاورت یک اندیس دیگر است. ولی در یک فهرست لینک شده، موقعیت هر گره جدید بر اساس این که چه زمانی ایجاد شده است، تعیین میشود. این گره جدید لزوماً از نظر فیزیکی مجاور همسایههای خود در فهرست نیست. نتیجه این است که گرههای فهرست لینک شده که در ترتیب فهرست «مجاور هم هستند»، بر حسب موقعیت واقعی درون تراشه RAM، به ندرت از نظر فیزیکی در کنار هم قرار میگیرند. از همین رو به دلیل روش عملکرد کش سیپییو، دسترسی به موقعیتهای مجاور حافظه سریع است و دسترسی به موقعیتهای حافظه به طور تصادفی به مقدار زیادی کندتر است. البته این توضیح کوتاهی بود، و توضیح دقیقتر این مسائل در ارتباط با فهرست لینک شده، کمی پیچیدهتر است. برای اطلاعات بیشتر به این مقاله مراجعه کنید.
اصول بنیادین یادگیری ماشین
برای درک شیوه استفاده از یادگیری ماشین جهت خلق مجدد خصوصیات ضروری یک جدول درهمسازی (و اندیسهای دیگر) بهتر است ایدهی اصلی مدلسازی آماری را بار دیگر مرور کنیم. یک مدل در مفهوم آماری خود تابعی است که بردارهایی را به عنوان ورودی میپذیرد و یک برچسب (برای طبقهبندی) یا مقدار عددی (برای رگرسیون) باز میگرداند. بردار ورودی شامل همه اطلاعات مرتبط در مورد نقاط دادهای و خروجی برچسب/عددی در واقع پیشبینی مدل است.
در مدلی که پیشبینی میکند آیا یک دانشجوی دبیرستانی میتواند وارد دانشگاه هاروارد شود یا نه، این بردار ممکن است شامل نمرات کلاسی دانشآموز، نمره آزمون نهایی، تعداد فعالیتهای فوق کلاسی که دانشآموز در آن شرکت کرده است و دیگر ارزشهای مرتبط با موفقیت تحصیلی وی باشد؛ برچسب نیز میتواند درست/نادرست باشد که نشاندهنده رفتن یا نرفتن دانشآموز به دانشگاه هاروارد است.
در مدلی که امکان اعطای تسهیلات بانکی را پیشبینی میکند، بردار ورودی میتواند شامل مقادیر رتبه اعتباری، تعداد حسابهای کارت اعتباری، فراوانی تأخیر در پرداختها، درآمد سالانه، و دیگر مقادیر مرتبط با وضعیت مالی افرادی باشد که برای وام درخواست میکنند. این مدل میتواند عددی بین 0 و 1 بازگرداند که نشان دهنده احتمال اعطای تسهیلات است.
به طور معمول یادگیری ماشین برای ایجاد یک مدل آماری استفاده میشود. متخصصین یادگیری ماشین، مجموعه دادههای عظیمی را به یک الگوریتم یادگیری ماشینی میدهند و نتیجه اجرای این الگوریتم، یک مدل تعلیمیافته است. یادگیری ماشین در اساسیترین مفهوم خود در مورد خلق الگوریتمهایی است که بتوانند بدون نیاز درک کنند که این که دادهها در عمل چه چیزی را نمایش میدهند و به طور خودکار مدلهای دقیقی از دادههای خام به دست آورند. این وضعیت، متفاوت از اشکال دیگر هوش مصنوعی است که در آن انسان دادهها را به طور وسیعی بررسی میکند و سرنخهایی در مورد این که معنی دادهها چیست (مثلاً از طریق تعریف شهود) به رایانه میدهد و شیوه استفاده رایانه از دادهها را به آن میآموزد (مثلاً با استفاده از مینیماکس یا A*).
با این وجود یادگیری ماشین در عمل به طور متناوب با تکنیکهای کلاسیک غیر یادگیری ترکیب میشود و عامل هوش مصنوعی به فراوانی برای هر دو تاکتیکهای یادگیری و غیریادگیری در جهت رسیدن به اهداف، مورد استفاده قرار میگیرد.
برای مثال هوش مصنوعی مشهور «Deep Blue» که شطرنج بازی میکند و مورد اخیر هوش مصنوعی گوگل به نام «AlphaGo» که Go بازی میکند، را در نظر بگیرید. دیپبلو یک هوش مصنوعی کاملاً غیر یادگیرنده است. در این مورد، برنامهنویسان رایانه در همکاری با متخصصین شطرنج، تابعی ایجاد کردهاند که وضعیت بازی، یعنی موقعیت مهرهها و نوبت بازی هر یک از بازیکنان را به عنوان ورودی میگیرد و مقداری باز میگرداند که نشان میدهد این وضعیت تا چه حد برای دیپبلو خوب است. دیپبلو هرگز چیزی یاد نمیگیرد، بازیکنان شطرنج با دقت بالایی تابع ارزیابی ماشین را کدگذاری کردهاند. خصوصیت اصلی دیپبلو، الگوریتم جستجوی درختی آن است که به آن امکان محاسبه همه حرکتهای ممکن را میدهد و همه پاسخهای احتمالی حریف را نیز تا چندین حرکت آینده پیشبینی میکند.

نمایش دیداری جستجوی درختی آلفاگو
آلفاگو نیز جستجوی درختی انجام میدهد. این هوش مصنوعی نیز مانند دیپبلو برای هر وضعیت احتمالی به چند حرکت آینده مینگرد. با این حال آلفاگو بر خلاف دیپبلو تابع ارزیابی خاص خود را ایجاد میکند که در آن دستورالعملهای صریحی از سوی خبرگان بازی گو ارائه نشده است. در این مورد تابع ارزیابی یک مدل یادگیرنده است. الگوریتم یادگیری ماشین آلفاگو بردار ورودی خود را که وضعیت صفحه بازی گو است، میگیرد. این وضعیت برای هر موقعیت شامل وجود مهره سفید، وجود مهره سیاه و یا عدم وجود مهره است و برچسبی که ارائه میدهد، مشخص میکند کدام بازیکن بازی را میبرد (سیاه یا سفید). الگوریتم یادگیری ماشین با استفاده از این اطلاعات، از میان صدها هزار بازی مختلف، هر وضعیت خاص صفحه را ارزیابی میکند. آلفاگو به خود میآموزد که کدام حرکتها از میان میلیونها نمونه موجود در مجموعه دادههایش، بالاترین احتمال برد را به ارمغان میآورند.
با این که مدل عملکردی هوش مصنوعی آلفاگو را تا حدود زیادی ساده بیان کردیم؛ اما برای داشتن ذهنیتی کلی مناسب است. برای مطالعه بیشتر در مورد آلفاگو میتوانید توضیحات خالقان آن را در اینجا بخوانید.
مدلها به عنوان اندیس و تفاوتهایی که با هنجارهای یادگیری ماشین دارند
محققان گوگل در مقاله خود این نوید را دادهاند که اندیسها خود مدل هستند؛ یا دستکم مدلهای یادگیری ماشین میتوانند به عنوان اندیس استفاده شوند. استدلال آنها چنین است که مدلها ماشینهایی هستند که ورودی میگیرند و برچسبی باز میگردانند. بنابراین اگر یک ورودی کلید باشد و برچسب تخمینی از آدرس حافظه باشد در این صورت مدل میتواند به عنوان یک اندیس عمل کند. با این که این تطبیق ساده به نظر میرسد؛ اما بدیهی است که مسئله اندیسگذاری، تطبیق کاملی با یادگیری ماشین ندارد. در ادامه برخی موضوعاتی که تیم گوگل مجبور شده است در آنها از هنجارهای یادگیری ماشین عدول کند تا به اهداف خود دست یابد را توضیح دادهایم.
یک مدل یادگیری ماشین به طور معمول بر روی دادههایی که میشناسد تعلیم مییابد و وظیفه آن ارائه تخمینی از دادههایی است که میبیند. زمانی که مشغول اندیسگذاری دادهها هستیم، ارائه تخمین قابل قبول نیست. تنها وظیفه یک اندیس آن است که موقعیت دقیق برخی دادهها را در حافظه بیابد. یک شبکه عصبی ساده (یا هر یادگیرنده دیگر ماشین) این سطح از دقت را ارائه نمیدهد. گوگل این مسئله را از طریق ردگیری بیشینه (مثبتترین) و کمینه (منفیترین) خطای تجربه شده برای هر گره در طی تمرین حل کرده است. با استفاده از این مقادیر به عنوان کرانها، اندیس یادگیری ماشین میتواند جستجویی را درون آن کرانها انجام دهد تا موقعیت دقیق عنصر را بیابد.
نکته اختلافی دیگر این است که متخصصین یادگیری ماشین به طور کلی باید مراقب اجتناب از «برازش بیش از حد» مدل خود با دادههای تمرینی باشند، چون چنین مدل بیشبرازشی باعث تولید پیشبینیهای خیلی دقیق برای دادههای که با آن تمرین داده شده است، میشود؛ اما غالباً بر روی دادههای خارج از مجموعه تمرین، عملکرد بسیار بدی ارائه میدهد. دادههای تمرینی دادههایی هستند که قرار است اندیسگذاری شوند و این مسئله موجب میشود که آنها دادههای آزمون نیز محسوب شوند. به دلیل این که جستجوها غالباً بر روی دادههای واقعی که اندیسگذاری شدهاند انجام میشوند، بیشبرازش در این کاربرد یادگیری ماشین تا حدی قابل قبولتر است. گرچه به طور همزمان اگر مدل با دادههای موجود برازش بالایی داده باشد، در این صورت افزودن یک آیتم جدید به اندیس ممکن است منجر به پیشبینیهای بسیار اشتباهی شود. چنان که در آن مقاله نیز اشاره شده است:
«... به نظر میرسد که تعادل جالبی بین تعمیمپذیری مدل و عملکرد در آخرین مراحل وجود دارد؛ هر چه پیشبینیهای مراحل بالاتر بهتر باشد، مدل نیز بیشبرازش بالاتری دارد و توانایی تعمیم به آیتمهای دادهای جدید کاهش مییابد.»
در نهایت باید گفت که تمرین دادن یک مدل معمولاً پرهزینهترین بخش فرایند است. متأسفانه در طیف وسیعی از کاربردهای پایگاه داده و دیگر کاربردهای اندیسگذاری، افزودن داده به اندیس امری کاملاً رایج است. تیم گوگل در خصوص این مسئله نیز نظر خود را به صراحت بیان کرده است:
«تاکنون نتایج ما بر روی ساختارهای اندیسی برای سیستمهای پایه از دادههای تنها خواندنی مستقر در حافظه متمرکز بوده است. همان طور که اشاره کردیم، طراحی کنونی حتی بدون اصلاح عمده برای جایگزینی ساختارهای اندیسی که در انبارهای دادهای استفاده میشوند و شاید تنها یک بار در طی روز بهروزرسانی شوند، کاملاً مناسب هستند. همین نکته در مورد BigTable که درختهای B به طور عمده به عنوان بخشی از فرایند ادغام SStable تولید میشوند، نیز صادق است».
نکته: SStable بخشی از ساختار BigTable گوگل است که در اینجا بیشتر میتوانید در مورد آن بخوانید.
یادگیری برای درهمسازی
مقاله تیم گوگل از میان همه گزینهها احتمال استفاده از مدل یادگیری ماشین برای جایگزینی یک تابع درهمسازی استاندارد را در نظر گرفته است. یکی از سؤالاتی که محققان علاقهمند بودهاند درک کنند این بوده است که آیا دانستن توزیع دادهها میتواند به ما کمک کند تا اندیسهای بهتری ایجاد کنیم؟ در راهبردهای سنتی مانند جابجایی-ضربی، درهمسازی murmur، ضرب در اعداد اول و .... که در بخشهای قبل بررسی کردیم، توزیع دادهها به طور کامل نادیده گرفته شدهاند. نتیجه این است که حتی در میان بسیاری از جداول درهمسازی کنونی محققان دریافتند که میتوانند مقدار فضای هدر رفته را تا میزان بسیار زیادی کاهش دهند.
این نتیجه چندان شگفتانگیز نیست. با تمرین دادن دادههای ورودی، تابع درهمسازی یادگیرنده میتواند توزیع یکنواختتری بر روی هر نوع فضا داشته باشد، زیرا مدل یادگیری ماشین، توزیع دادهها را میفهمد. با این حال این مسیر قدرتمندی برای کاهش مقدار فضای ذخیرهسازی مورد نیاز برای اندیسهای جدول درهمسازی نیز محسوب میشود. البته این مسئله خود مزایا و معایبی دارد، چون مدل یادگیری ماشین محاسبه کندتری نسبت به توابع درهمسازی استاندارد که قبلاً دیدیم دارد و نیازمند مرحله تمرینی است که در تابع استاندارد درهمسازی مطرح نیست.
شاید بتوان توابع درهمسازی مبتنی بر یادگیری ماشین را در موقعیتهایی که استفاده مؤثر از حافظه، دغدغهای ضروری است و توان محاسباتی اهمیت حادی ندارد، مورد استفاده قرار داد. تیم تحقیقاتی گوگل/امآیتی پیشنهاد میکنند که انباره دادهها استفاده مناسبی از این تکنیک محسوب میشود، زیرا اندیسها قبلاً و در حدود روزی یک بار در فرایندهای پر هزینه ایجاد شدهاند. استفاده از زمان محاسباتی اندکی بیشتر برای ذخیرهسازی حافظه بیشتر، میتواند در اغلب موقعیتهای انبار دادهای مزیتهای بالایی داشته باشد.
اما وقتی درهمسازی کوکو (cuckoo) را در نظر میگیریم، قضیه اندکی پیچیدهتر میشود.
درهمسازی کوکو
درهمسازی کوکو در سال 2001 ابداع شده است و به نام خانواده پرندگان کوکو (فاخته) نامگذاری شده است. درهمسازی کوکو جایگزینی برای زنجیرهسازی و کاوش خطی در زمینه مدیریت تصادم محسوب میشود و جایگزین تابع درهمسازی نیست. راهبرد آن به این دلیل کوکو نامیده شده است که در برخی گونههای کوکو جنس ماده که آماده تخمگذاری است، به لانه پرندگان مجاور رفته و تخمهای آنها را از لانه بیرون میاندازد تا تخمهای خود را در لانهشان قرار دهد. در الگوریتم درهمسازی کوکو نیز دادههای ورودی، همانند پرندگان کوکو که تخمهای پرندگان مجاور را میدزدند، آدرس دادههای قدیمی را میربایند.
شیوه عمل این گونه است که وقتی یک جدول درهمسازی ایجاد میکنید، در واقع بلافاصله جدول را به دو فضای آدرس تقسیم میکنید که آنها را آدرس اولیه و آدرس ثانویه مینامیم. به علاوه دو تابع درهمسازی مستقل را برای هر کدام از فضاهای آدرس راه میاندازیم. این توابع درهمسازی میتوانند مشابه باشند. برای نمونه آنها میتوانند خانواده «مضرب اولیه» را تشکیل دهند که در آن هر تابع درهمسازی از عدد اول متفاوتی استفاده میکند. ما این توابع را توابع درهمسازی اولیه و ثانویه مینامیم.
در ابتدا ورودیهای یک درهمسازی کوکو تنها از تابع اولیه و فضاهای آدرس اولیه استفاده میکنند. وقتی تصادمی رخ دهد، دادههای جدید جایگزین دادههای قدیمی میشوند و دادههای قدیمی مجدداً با استفاده از تابع درهمسازی ثانویه، درهمسازی میشوند و در فضای آدرس ثانویه قرار میگیرند.
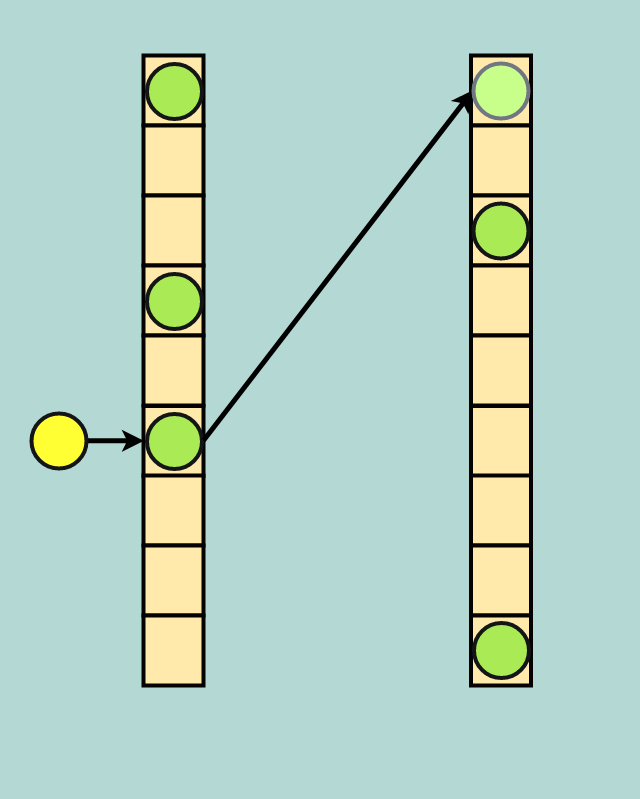
کوکو برای تصادم: دادههای زرد رنگ جایگزین دادههای سبز میشوند و دادههای سبز در فضای آدرس ثانویه قرار میگیرند.
اگر این فضای آدرس ثانویه قبلاً اشغال شده باشد، جایگزینی دیگری رخ میدهد و دادهها در فضای آدرس ثانویه مجدداً به آدرس فضای اولیه باز میگردد. از آنجا که ممکن است یک حلقه نامتناهی از این جایگزینیها صورت گیرد، معمولاً یک حد آستانه از جایگزینیها برای هر درج تعیین میشود. اگر این تعداد جایگزینی حاصل شود، جدول از نو ساخته میشود که میتواند شامل تخصیص فضای بیشتر برای جدول و/یا انتخاب تابعهای درهمسازی جدید باشد.
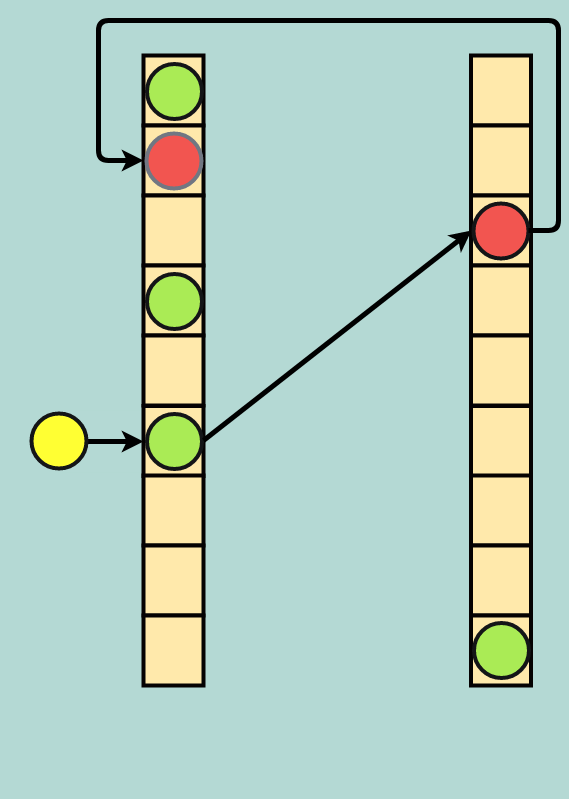
جایگزینی دوگانه: دادههای ورودی جدید زرد رنگ جایگزین دادههای سبز میشوند، دادههای سبز جایگزین قرمز میشوند و دادههای قرمز در فضای آدرس اولیه قرار میگیرند.
این راهبرد در سناریوهایی که محدودیت حافظه وجود دارد، کارایی خواهد داشت. این «قدرت انتخاب دوگانه» در الگوریتم درهمسازی کوکو عملکرد پایداری را حتی در نرخهای استفاده بسیار بالا از خود نشان میدهد. این نکتهای است که در مورد الگوریتمهای زنجیرهسازی یا کاوش خطی صدق نمیکند.
بِیلیس و تیم تحقیقاتی وی در دانشگاه استنفورد دریافتند که با چند بهینهسازی کوچک، درهمسازی کوکو میتواند بسیار سریع باشد و عملکرد بالایی حتی در استفادههای 99 درصدی داشته باشد. درهمسازی کوکو اساساً میتواند در تابعهای درهمسازی با یادگیری ماشین بدون یک مرحله تمرینی پر هزینه از طریق بهرهگیری از قدرت انتخاب دوگانه کاربرد بالایی بیابید.
آینده اندیسگذاری
در نهایت باید گفت که همگان در مورد قابلیت ساختارهای اندیسگذاری که یادگیرنده هستند، هیجانزده هستند. بدین ترتیب ابزارهای یادگیری ماشین بیشتری در اختیار خواهیم داشت و پیشرفتهای سختافزاری مانند TPU (مخفف Tensor processing unit، واحد پردازش تنسور که سخت افزاری به صورت مدار ASIC است که گوگل به طور اختصاصی برای پردازش یادگیری ماشین شبکه عصبی توسعه داده است.) باعث میشوند که عملیاتهای یادگیری ماشین سریعتر انجام یابند و اندیسگذاری به طور فزایندهای از راهبردهای یادگیری ماشین بهرهمند شود. الگوریتمهای زیبایی مانند درهمسازی کوکو به ما خاطرنشان میسازند که یادگیری ماشین نوشداروی هر دردی نیست. تحقیقاتی که توان خارقالعاده تکنیکهای یادگیری ماشین و همچنین نظریههای قدیمی «توان انتخاب دوگانه» را با هم ترکیب میکنند، باعث گسترش مرزهای کارآمدی و توان رایانهها خواهند شد.
به نظر محتمل نمیآید که بنیادهای مفهوم اندیسگذاری، یکشبه بهوسیله تاکتیکهای یادگیری ماشین جایگزین شوند؛ اما ایده اندیسهای خودتنظیم مفهومی قدرتمند و هیجانانگیز است. همچنان که رفتهرفته یادگیری ماشین، جای بیشتری در زندگی ما باز میکند و همینطور که به بهبود کارایی رایانهها در پردازشهای یادگیری ماشین ادامه میدهیم، ایدههای جدیدی که این پیشرفتها را تسهیل میکنند، بیشک راه خود را به حوزه کاربردهای عملی خواهند گشود. نسخههای بعدی پایگاههای داده داینامودیبی (DynamoDB) یا کاساندرا (Cassandra) ممکن است به طور کامل از تاکتیکهای یادگیری ماشین بهرهمند باشند؛ پیادهسازیهای آتی پستگرساسکیوال یا مایاسکیوال نیز میتوانند در نهایت چنین راهبردهایی را به خدمت بگیرند. سرانجام این به موفقیت تحقیقاتی آتی بستگی خواهد داشت که آیا مسیر راهبردهای غیر یادگیری کنونی را ادامه میدهیم یا تاکتیکهای کاملاً نوین انقلاب هوش مصنوعی را برمیگزینیم.
اگر این نوشته مورد توجه شما واقع شده است، موارد زیر نیز احتمالاً برای شما جذاب خواهند بود:
- آموزش مروری بر توابع Hash و خطر تصادم در آن ها
- مقدمهای بر یادگیری ماشین
- آموزش یادگیری ماشین
- آموزش درهم سازی در ساختمان داده
- گنجینه آموزش های یادگیری ماشین و داده کاوی
- آموزش ذخیره و بازیابی اطلاعات
- آموزش ساختمان داده ها
- مجموعه آموزشهای داده کاوی و یادگیری ماشین
==












