کات ست در گراف — به زبان ساده

در آموزش‌های قبلی مجله فرادرس درباره درخت در گراف بحث شد. در این آموزش قصد داریم مفهوم کات ست در گراف را بررسی کنیم. اگر با برخی اصطلاحات این آموزش آشنا نیستید، به آموزش «گراف — تعاریف و انواع به زبان ساده» مراجعه کنید.

در ابتدا به بیان یک قضیه ساده راجع به گراف همبند می‌پردازیم.

قضیه ۱

هر گراف ساده با $$n$$‌ راس و تعداد یال‌های بیشتر از $$(n-1)(n-2)/2$$، همبند است.

فیلم آموزش نظریه گراف و کاربردها در فرادرس

کلیک کنید

در گراف‌های همبند همواره این سوال مطرح می‌شود که همبندی گراف به چه ترتیب است. یک تفسیر ساده این است که پرسیده شود چه تعداد یال یا راس باید حذف شود تا گراف ناهمبند شود. این سوال‌ها در این آموزش، پاسخ داده می‌شود.

مجموعه ناهمبند کننده

یک «مجموعه ناهمبند کننده» (Disconneting Set) در گراف همبند $$G$$، به مجموعه یال‌هایی گفته می‌شود که حذف آنها باعث ناهمبند شدن گراف $$G$$‌ می‌شود. برای مثال گراف زیر را در نظر بگیرید:

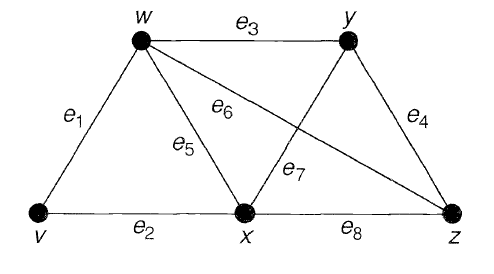
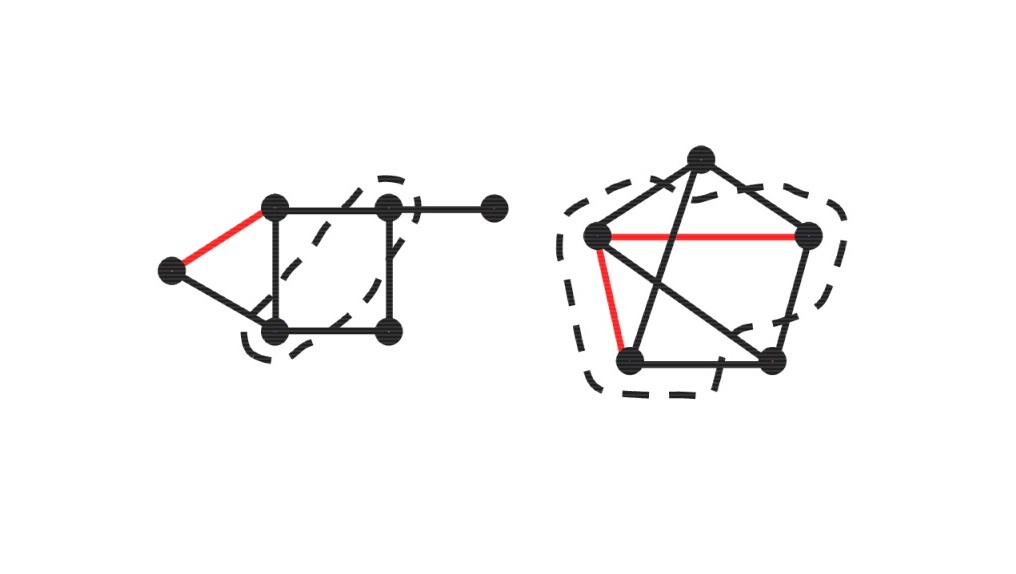
در این گراف، مجموعه‌های $$\{ e_1 , e_2 , e_5\}$$ و $$\{ e_3 , e_6 , e_7 , e_8 \}$$، مجموعه‌های ناهمبند کننده گراف $$G$$ هستند. با حذف یال‌های دومین مجموعه اشاره شده از این گراف، به گراف ناهمبند زیر خواهیم رسید:

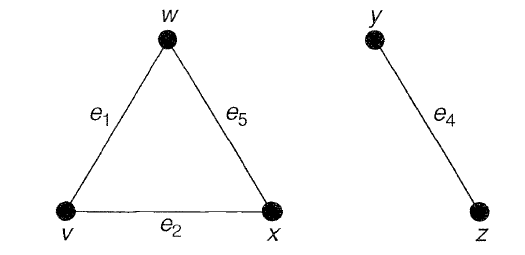
کات ست گراف

«کات ست» (cutset) یک گراف، یک مجموعه ناهمبند کننده است که هیچ زیرمجموعه‌ای از آن ناهمبند کننده نیست. در مثال بالا، مجموعه ناهمبندکننده دوم، کات ست است و مجموعه اول کات ست نیست، به این دلیل که زیرمجموعه $$\{ e_1 , e_2\}$$ از مجموعه اول نیز، ناهمبند کننده است.

فیلم آموزش گراف ها و گروه ها در فرادرس

کلیک کنید

باید توجه کرد که با حذف یال‌های کات ست، گراف دقیقا به دو مولفه تقسیم می‌شود.

فرض کنید کات ست گراف، فقط یک یال $$e$$ دارد. این یال، «پل» (Bridge) نامیده می‌شود. یک مثال از پل در شکل زیر نشان داده شده است:

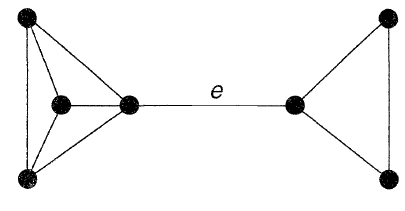
تعریف‌های بالا را می‌توان به گراف‌های ناهمبند نیز تعمیم داد. مجموعه ناهمبند کننده در گراف ناهمبند $$G$$، به مجموعه یال‌هایی گفته می‌شود که با حذف آنها، مولفه‌های گراف $$G$$ افزایش پیدا می‌کند. به همین ترتیب، کات‌ ست گراف $$G$$ به مجموعه ناهمبند کننده‌ای گفته می‌شود که هیچ زیرمجموعه‌ای از آن، ناهمبند کننده نیست.

در گراف همبند $$G$$، «همبندی یال‌ها» (Edge Connectivity) به اندازه کوچکترین کات ست گراف $$G$$ گفته می‌شود. همبندی یال‌های گراف $$G$$ با نماد $$\lambda (G)$$ نشان داده می‌شود. بنابراین $$\lambda (G)$$ کمترین تعداد از یال‌ها است که برای ناهمبند شدن گراف $$G$$ لازم است. در مثال شکل (۱)، داریم:

$$\lambda (G) =2$$

این عدد، مربوط به کات‌ ست این گراف یعنی $$\{e_1 , e_2 \}$$ است. همچنین اگر $$\lambda (G) \geq k$$ باشد، گفته می‌شود که گراف $$G$$ یک گراف $$k$$ - یال همبند است. بنابراین گراف شکل (۱)، یک یال همبند و دو یال همبند است، اما سه یال همبند نیست.

مجموعه جدا کننده

در این قسمت از آموزش به بررسی این سوال می‌پردازیم که اگر یک یا چند رأس از گراف حذف شود، چه اتفاقی می‌افتد. «مجموعه جدا کننده» (Seperating Set) در گراف همبند $$G$$، به مجموعه رئوسی گفته می‌شود که حذف آنها موجب ناهمبند شدن $$G$$ خواهد شد. ذکر این نکته ضروری است که با حذف یک رأس از گراف، یال‌های متصل به آن را‌ٔس نیز باید حذف شوند.

مثلا در گراف شکل (۱)، مجموعه‌های $$\{ w,x \}$$ و $$\{ w,x,y \}$$، مجموعه‌های جدا کننده گراف $$G$$ هستند. پس از حذف اولین مجموعه جدا کننده از گراف شکل (۱)، گراف ناهمبند زیر حاصل می‌شود:

اگر مجموعه جداکننده فقط شامل یک رأس $$v$$ باشد، آن را «رأس برشی» (Cut-Vertex) گراف می‌نامند. همچنان که بیان شد، می‌توان این تعریف‌ها را برای گراف‌های ناهمبند نیز به کار برد. برای مثال در شکل زیر، رأس $$v$$ یک راس برشی است، زیرا با حذف این رأس کل گراف ناهمبند می‌شود:

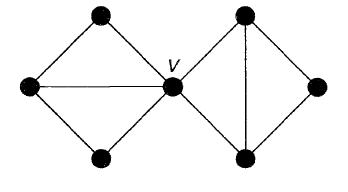
«همبندی رئوس» (Vertex Connectivity) در گراف همبند $$G$$، به اندازه کوچکترین مجموعه جدا کننده گراف $$G$$ گفته می‌شود. همبندی رئوس با نماد $$\kappa (G)$$ نشان داده می‌شود. بنابراین $$\kappa (G)$$ کمترین تعداد رئوس است که گراف $$G$$ را ناهمبند می‌کند. در گراف شکل (۱)، $$\kappa (G) = 2$$ است. این عدد مربوط به مجموعه جدا کننده $$\{ w,x \}$$ است.

در گراف $$G$$، اگر $$\kappa (G) \geq k$$ باشد، آن را $$k$$‌ همبند می‌نامند. بنابراین گراف شکل (۱)، یک همبند و دو همبند هست اما سه همبند نیست.

می‌توان ثابت کرد که اگر $$G$$‌ یک گراف همبند باشد، آنگاه $$\kappa (G) \leq \lambda (G)$$.

درجه حلقه و درجه کات‌ست

همانطور که در تعریف درخت پوشا در مبحث درخت در گراف مطرح کردیم، می‌توان با در نظر گرفتن گراف همبند $$G$$ و حذف هر یال از حلقه گراف و ادامه این عمل به درخت پوشای گراف رسید.

فیلم آموزش ساختارهای جبری، گراف ها و ماتریس ها در فرادرس

کلیک کنید

به طور عمومی‌تر ، اگر $$G$$ یک گراف دلخواه با $$n$$ رأس و $$m$$‌ یال و $$k$$ مولفه باشد، می‌توان این فرآیند را برای هریک از مولفه‌های این گراف تکرار کرد. نتیجه این عمل را «جنگل پوشا» (Spanning Forest) می‌نامند. کل تعداد یال‌های حذف شده در این فرآیند، درجه حلقه $$G$$ نامیده می‌شود. «درجه حلقه» (Cycle Rank) گراف $$G$$، با نماد $$\gamma(G)$$ نشان داده می‌شود. درجه حلقه یک گراف برابر است با:

$$\gamma (G)=m-n+k$$

که در آن، $$\gamma(G)$$ یک عدد صحیح غیر منفی است.

به تعداد یال‌های یک جنگل پوشا، «درجه کات ست» (Cutset Rank) گفته می‌شود. درجه کات ست با نماد $$\xi (G)$$ نشان داده می‌شود و برابر است با:

$$\xi (G) =n-k$$

در ادامه چند خاصیت جالب جنگل‌های پوشا را ذکر کنیم.

مکمل جنگل پوشای $$T$$ از گراف غیر ساده $$G$$، گرافی است که با حذف یال‌های $$T$$ از گراف $$G$$ به دست می‌آید.

قضیه ۲

اگر $$T$$، یک جنگل پوشای دلخواه از گراف $$G$$ باشد،

1. هر کات‌ست گراف $$G$$، یک یال مشترک با $$T$$ دارد.
2. هر حلقه از گراف $$G$$، یک یال مشترک با مکمل $$T$$ دارد.

اثبات:

1. فرض کنید $$C^ \ast$$، کات‌ست گراف $$G$$ باشد. حذف این کات‌ست، یکی از مولفه‌های $$G$$ را به دو زیر گراف $$H$$ و $$K$$ تقسیم می‌کند. می‌دانیم که $$T$$ یک جنگل پوشا است. پس باید شامل یک یال باشد که یک رأس از $$H$$ را به یک راس از $$K$$ متصل می‌کند. و این یال، یک یال ضروری است.
2. فرض کنید $$C$$، حلقه‌ای از $$G$$ باشد که هیچ یال مشترکی با $$T$$ ندارد. پس گراف $$T$$ باید حلقه $$C$$ را در برداشته باشد که این گزاره یک تناقض است.

ایده جنگل پوشای $$T$$ از گراف $$G$$ به مجموعه حلقه‌های بنیادی $$T$$ بسیار مرتبط است.

فرض کنید یک یال به $$T$$ اضافه شود که در $$G$$ وجود دارد، اما در $$T$$ وجود ندارد. به این ترتیب در گراف $$T$$، یک حلقه یکتا خواهیم داشت. حال فرض کنید این فرآیند ادامه یابد و به گراف، یال‌هایی اضافه شود که در جنگل وجود ندارند و در $$G$$ وجود دارند. با اضافه شدن این یال‌ها، مجموعه بنیادی حلقه‌ها مربوط به جنگل $$T$$ تشکیل می‌شود.

در برخی موارد، ما به این جنگل پوشای خاص تمایلی نداریم، بنابراین این مجموعه را «مجموعه حلقه‌های بنیادی» (Fundamental Set of Cycles) از گراف $$G$$‌ می‌نامیم. ذکر این نکته ضروری است که تعداد حلقه‌های موجود در هر مجموعه حلقه بنیادی با درجه حلقه گراف $$G$$، برابر است.

در شکل زیر یک گراف و درخت پوشای آن نشان داده شده است:

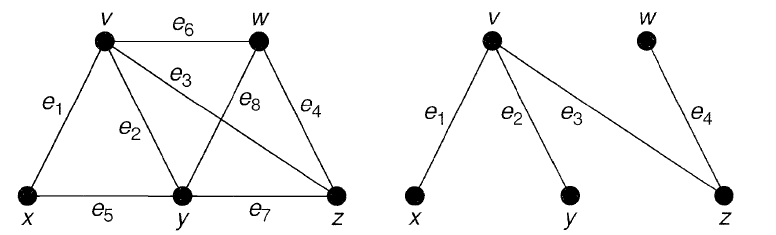
در شکل زیر، زیر مجموعه حلقه‌های بنیادی گراف شکل (۶) نشان داده شده است:

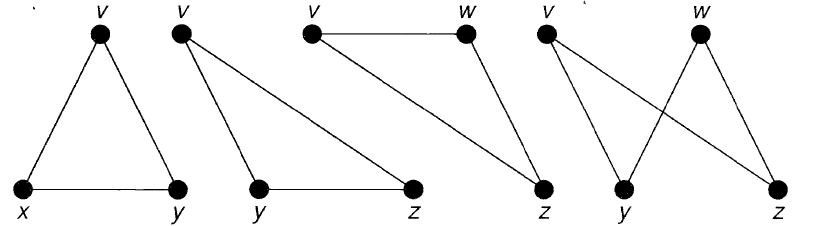
حال به تعریف یک مجموعه بنیادی از کات‌ست‌های گراف $$G$$ مربوط به جنگل پوشای $$T$$ می‌پردازیم. با حذف هر یال از $$T$$، مجموعه رئوس گراف به دو مجموعه گسسته $$V_1$$ و $$V_2$$ تبدیل می‌شود. مجموعه‌ای از همه یال‌های $$G$$ که یکی از  رئوس $$V_1$$ را به یکی از رئوس $$V_2$$ متصل می‌کند، کات‌ست گراف $$G$$ است.

با ادامه این فرآیند و حذف هر یال از $$T$$، می‌توان به مجموعه کات‌ست‌های مربوط به $$T$$ رسید. تعداد کات‌ست‌ها در هر مجموعه بنیادی باید با درجه کات‌ست $$G$$، برابر باشد. برای درخت پوشای داده شده در شکل (۶)، مجموعه کات‌ست‌های گراف برابر است با:

$$\{ e_1 , e_5 \}, \, \{ e_2 , e_5 , e_7 , e_8\}, \{ e_3 , e_6 , e_7 , e_8 \}, \{ e_4 , e_6 , e_8\}$$

^^