آشنایی کامل با مفهوم تنش — بخش اول: تاریخچه و مفاهیم اساسی

در «مکانیک محیط‌های پیوسته» (Continuum Mechanics)، نیروهای داخلی اعمال شده توسط ذرات مجاور درون جسم به یکدیگر، به وسیله یک کمیت فیزیکی به نام «تنش» (Stress) بیان می‌شود. به عنوان مثال، در صورت اعمال فشار به مایع درون یک محفظه بسته نیز هر ذره توسط تمام ذرات دربرگیرنده خود تحت فشار قرار خواهد گرفت. به علاوه، طبق قانون سوم نیوتون، دیواره‌های محفظه و سطح اعمال کننده فشار (پیستون) نیز در برابر واکنش‌های ذرات از خود عکس العمل نشان خواهند داد. در یک مثال دیگر، اگر بر روی یک میله عمودی وزنه ای قرار داده شود، تمام ذرات درون میله به ذرات مجاور زیرین خود فشار وارد می‌کنند. در واقع، تمام این نیروهای ماکروسکوپی (قابل مشاهده)، نتیجه نهایی تعداد بسیار زیادی از نیروهای بین مولکولی و برخوردهای بین ذرات درون آن مولکول‌ها هستند. تنش، معمولاً با حرف کوچک یونانی سیگما (σ) نمایش داده می‌شود.

یکی دیگر از کمیت‌های مهم در مکانیک محیط‌های پیوسته، «کرنش» (Strain) است. این کمیت معیاری برای تغییر شکل مواد به حساب می‌آید. مکانیسم‌های مختلفی از قبیل اعمال نیروی‌های خارجی (مانند تنش)، نیروی‌های داخلی (مانند جاذبه) یا نیروهای سطحی (مانند نیروی اتصال، فشار دربرگیرنده یا اصطکاک) می‌توانند منجر به ایجاد کرنش در یک ماده شوند. در مواد جامد، تمام کرنش‌ها (تغییر شکل‌ها) باعث ایجاد تنش الاستیک می‌شوند. این تنش همانند نیروی عکس‌العمل فنر رفتار می‌کند و ماده را به حالت پیش از تغییر شکل بازمی‌گرداند. در مایعات و گازها، تنها تغییر شکل‌های دارای تنش الاستیک هستند که می‌توانند منجر به تغییر حجم مواد شوند. اگرچه، در صورت تغییر شکل تدریجی مواد، معمولاً مقداری تنش ویسکوز در آن‌ها (حتی سیالات) به وجود می‌آید که در خلاف جهت تغییرات صورت گرفته عمل می‌کند. تنش‌های الاستیک و ویسکوز معمولاً به عنوان «تنش مکانیکی» (Mechanical Stress) شناخته می‌شوند. تنش می‌تواند به‌صورت حرارتی بوده و در نتیجه انبساط گرمایی ایجاد شود.

در برخی از مواقع، با وجود قرارگیری مواد در شرایط خاصی مانند موارد زیر نیز امکان به ایجاد تنش (قابل توجه) وجود دارد:

فیلم آموزش مقاومت مصالح – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

• تغییر شکل‌های ناچیز یا عدم وجود تغییر شکل: مدل‌سازی جریان آب
• عدم اعمال نیروهای خارجی: بتن‌های پیش‌تنیده و شیشه‌های حرارت دیده
• عدم اعمال نیروی خالص: تغییر دما یا ترکیب شیمیایی
• اعمال میدان‌های الکترومغناطیس خارجی: مواد پیزوالکتریک یا مَگنِتو اِستریکتیو (تغییر خاصیت کشسانی با قرارگیری در میدان مغناطیسی)

در برخی از مواقع، رابطه بین تنش مکانیکی، تغییر شکل و نرخ تغییر شکل کمی پیچیده است. در صورت کوچک بودن کمیت‌ها (به اندازه کافی)، استفاده از تخمین‌های خطی می تواند برای مسائل کاربردی مناسب باشد. تنش‌های که از محدوده مقاومتی مواد بزرگ‌تر هستند، منجر به ایجاد تغییر شکل دائمی (جریان پلاستیک، شکاف، حفره و غیره) یا حتی تغییر در ساختار بلوری و ترکیب شیمیایی خواهند شد.

در برخی از شاخه‌های علوم مهندسی، واژه تنش مترادف با نیروی داخلی است. به عنوان مثال، در تحلیل خرپاها، به جای استفاده از مقدار نیرو تقسیم بر مساحت هر عضو، ممکن است تنها از برآیند نیروی کششی یا فشاری اعمال شده به آن استفاده شود.

تاریخچه آشنایی با تنش‌‌

درک بشر از وجود تنشِ درون مواد، به دوران باستان بازمی‌گردد. آشنایی با این مفهوم تا قرن 17 ام میلادی، بیشتر به صورت بصری و به واسطه علوم تجربی بود. با این وجود، همین درک و آشنایی محدود با مفهوم تنش، به طور شگفت‌انگیزی منجر به ایجاد تکنولوژی‌های پیچیده‌ای از قبیل شیشه‌گری و کمان کامپوزیت شد.

معماران و سازندگان در طی چندین هزار سال یاد گرفتند که چگونه وسایل مبتکرانه‌ای مانند سر ستون، قوس، گنبد، خرپا و پشت‌بندهای معلق، بلوک‌های سنگی و تیرهای چوبی (با شکل‌های مختلف) را در کنار یکدیگر قرار دهند تا تحمل، انتقال و توزیع تنش به بهترین شکل ممکن صورت گیرد.

معماران دوران باستان و قرون وسطا، چندین روش هندسی و فرمول ساده را برای محاسبه ابعاد مناسب ستون و تیرهای مورد استفاده در سازه‌ها توسعه دادند. با این وجود، درک مفهوم تنش به صورت علمی، پس از اختراع ابزارهای مورد نیاز در قرن 17 و 18 میلادی میسر شد. روش آزمایش دقیق «گالیلئو گالیله» (Galileo Galilei)، هندسه تحلیلی و دستگاه مختصات «رنه دکارت» (René Descartes) و حساب دیفرانسیل و قوانین حرکتی «آیزاک نیوتون» (Isaac Newton) از مواردی هستند که زمینه آشنایی علمی با مفهوم تنش را فراهم کردند. «آگوستین لویی کوشی» (Augustin-Louis Cauchy)، ریاضیدان، مهندس و فیزیکدان فرانسوی، اولین مدل ریاضی دقیق و عمومی برای تنش در یک محیط همگن را با بهره‌گیری از ابزارهای اشاره شده ارائه کرد. کوشی دریافت که نیروهای موجود در سراسر یک سطح فرضی، تابعی از بردارهای نرمال آن سطح است. به علاوه، این توابع باید به صورت متقارن (گشتاور کلی صفر) باشد.

آشنایی با مفهوم علمی تنش در مایعات نیز با دستاوردهای نیوتون و ارائه معادله دیفرانسیل نیروهای اصطکاکی (تنش برشی) در جریان آرام موازی امکان‌پذیر شد.

تعریف تنش

تنش به صورت نیرو در یک محدوده کوچک تقسیم بر واحد سطح و در تمام جهات آن محدوده تعریف می‌شود. از آنجایی که تنش از یک کمیت اصلی فیزیکی (نیرو) و یک کمیت کاملاً هندسی (مساحت) به دست می‌آید، می‌توان آن را مانند سرعت، گشتاور و انرژی به عنوان یک کمیت اصلی در نظر گرفت. کمیت‌های اصلی، بدون در نظر گرفتن ماهیت مواد و علائم فیزیکی‌شان مورد تحلیل قرار می‌گیرند.

فیلم آموزش مقاومت مصالح – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

در حوزه مکانیک محیط‌های پیوسته، تنش به عنوان یک مفهوم ماکروسکوپی شناخته می‌شود. به همین دلیل، برای بررسی تنش، ذرات مورد تحلیل باید به اندازه‌ای کوچک باشند که بتوان ساختار و حالت آن‌ها را همگن در نظر گرفت. به علاوه، این ذرات باید به اندازه‌ای بزرگ باشند که بتوان اثرات کوانتومی و جزئیات حرکت مولکول‌های آن‌ها را نادیده گرفت. با توجه این فرضیات، میزان نیروی بین دو ذره، از میانگین‌گیری تعداد زیادی نیروی اتمی موجود در بین مولکول‌ها به دست می‌آید و توزیع کمیت‌های فیزیکی از قبیل جرم، سرعت و نیروهای داخلی اجسام سه‌بعدی (مانند جاذبه) به صورت یکنواخت در نظر گرفته می‌شود. در برخی از موارد موارد نظیر بررسی دانه‌های یک میله فلزی یا الیاف یک تکه چوب می‌توان فرض کرد که بزرگی ذرات این مواد برای میانگین‌گیری خواص میکروسکوپی مناسب است.

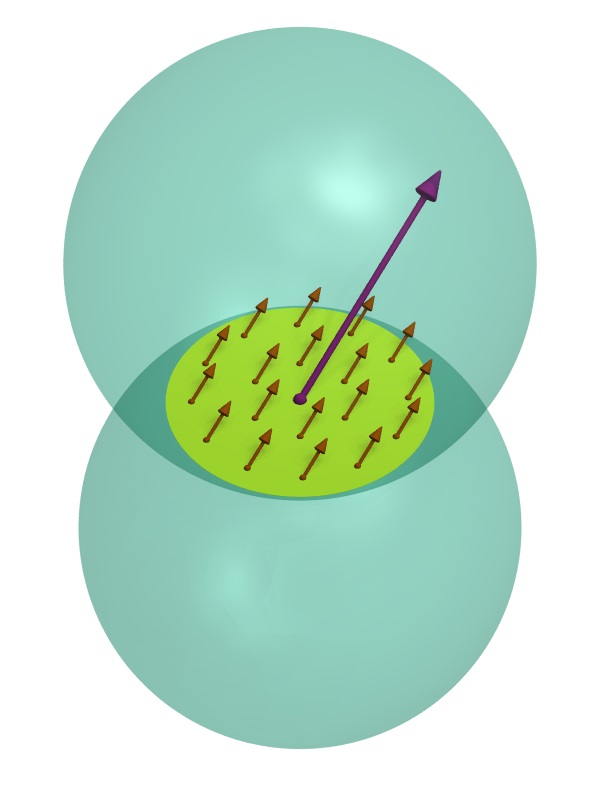
از نظر کمی، تنش حاصل از بردار کشش کوشی (T) به صورت نیروی کششی بین بخش‌های مجاور یک ماده (F) بر روی یک سطح جداکننده فرضی (S) تقسیم بر مساحت آن سطح تعریف می‌شود (شکل زیر). در سیالات ساکن، نیرو به صورت عمود بر سطح بوده و مفهوم تنش با فشار یکسان است. در جامدات یا جریان مایعات ویسکوز، ممکن است که نیرو بر سطح عمود نباشد. از این‌رو، تنش موجود در یک سطح باید به صورت برداری در نظر گرفته شود. به علاوه، در این حالت، جهت و مقدار تنش عموماً به جهت‌گیری سطح بستگی دارد. به این ترتیب، حالت تنش باید توسط تانسوری به نام تانسور تنش (کوشی) تعریف شود. این تانسور، یک تابع خطی است که بردار نرمال (n) در صفحه (S) را به تنش (T) در صفحه (S) مرتبط می‌کند. با توجه به دستگاه مختصات انتخاب شده می‌توان تانسور تنش کوشی را به صورت یک ماتریس 3*3 نمایش داد. حتی درون اجسام همگن نیز احتمال تغییر تنش در بخش‌های مختلف و با گذشت زمان وجود دارد؛ بنابراین، تنش درون مواد به طور کلی یک میدان تانسوری وابسته به زمان است.

تنش نرمال و تنش برشی

تنش اعمال شده (T) از طرف ذره (P) به ذره (Q) بر روی سطح (S) دارای یک جهت مشخص نسبت به S است. به طور کلی، بردار T را می‌توان به صورت حاصل جمع دو مؤلفه تنش بیان کرد. این دو مؤلفه شامل تنش نرمال فشاری یا کششی (عمود بر S) و تنش برشی (موازی با S) می‌شوند.

در صورت مشخص بودن بردار یکه نرمال (n) در سطح S، می‌توان مؤلفه نرمال تنش را توسط یک عدد و با ضرب نقطه‌ای (T.n) به دست آورد. اگر ذره P در حال کشیدن ذره Q باشد (تنش کششی)، علامت تنش مثبت و اگر در حال وارد کردن فشار باشد (تنش فشاری)، علامت تنش منفی خواهد بود. مؤلفه برشی تنش نیز به صورت بردار و با استفاده از رابطه (T-(T.n)n) محاسبه می‌شود.

واحد تنش

در تحلیل ابعادی، بُعد کمیت‌های تنش و فشار مشابه یکدیگر است و معمولاً اندازه‌گیری مؤلفه‌های تنش بر اساس واحدهای فشار صورت می‌گیرد. به این منظور، در «سیستم بین‌المللی یکاها» (International System of Units) یا اصطلاحاً «SI»، از واحد پاسکال (Pa) یا نیوتون بر متر مربع (N/m²) و در «سیستم یکاهای انگلیسی» (Imperial Units)، از واحد پوند بر اینچ مربع (psi) برای بیان مقدار تنش استفاده می‌شود. تنش‌های مکانیکی معمولاً مقداری بزرگ‌تر از یک میلیون پاسکال (MPa) دارند. به همین علت، متداول‌ترین واحد برای بیان مقدار تنش، مگا پاسکال (MPa) است.

فیلم آموزش مقاومت مصالح 1 و 2 – مرور و حل مساله در فرادرس

کلیک کنید

عوامل فیزیکی و اثرات تنش

وجود تنش در یک جسم می‌تواند به عوامل فیزیکی مختلفی از جمله عوامل خارجی و فرآیندهای داخلی ارتباط داشته باشد. برخی از این عوامل مانند تغییر دما و فاز یا میدان‌های الکترومغناطیسی در درون جسم رخ می‌دهند و با توجه مکان و زمان به طور مداوم تغییر می‌کنند. در عوامل دیگر نظیر بارگذاری‌های خارجی، اصطکاک، فشار محیط و نیروهای اتصال، امکان تمرکز تنش و نیرو در سطوح، خطوط یا نقطه‌های بخصوص جسم وجود دارد. این تمرکز تنش یا نیرو معمولاً در بازه‌های زمانی کوتاه رخ می‌دهند (مانند ضربه‌های ناشی از برخورد اجسام). به طور کلی، توزیع تنش در یک جسم به صورت یک تابع پیوسته چند ضابطه‌ای از زمان و مکان تعریف می‌شود.

معمولاً تنش با اثرات مختلف بر روی مواد مانند تغییر در خواص فیزیکی آن‌ها (دوشکستی، قطبش پذیری و نفوذپذیری) نیز ارتباط دارد. اعمال تنش توسط عوامل خارجی در اغلب موارد باعث ایجاد کرنش (تغییر شکل) در ماده می‌شود که گاهی اوقات به اندازه‌ای کوچک است که نمی‌توان آن را تشخیص داد. در مواد جامد، این نوع کرنش منجر به ایجاد تنش الاستیک داخلی خواهد شد (متناظر با نیروی عکس‌العمل در فنر کشیده شده). تنش الاستیک تمایل دارد ماده را به وضعیت قبل از تغییر شکل بازگرداند. سیالات (مایعات، گازها و پلاسما) تنها قادر به عکس‌العمل در مقابل تغییر شکل‌هایی هستند که باعث تغییر حجم آن‌ها شوند. با این وجود، اگر تغییر شکل سیالات با گذشت زمان متغیر باشد، تنشی موسوم به «تنش ویسکوز» (Viscous Stress)در آن‌ها به وجود می‌آید که در جهت خلاف تغییرات به وجود آمده عمل می‌کند.

همان طور که پیش از نیز اشاره شده، رابطه بین تنش با دلایل و اثرات آن از جمله تغییر شکل و نرخ تغییر شکل پیچیده است و تنش‌های بزرگ (بیشتر از محدوده مقاومت ماده) می‌توانند منجر به ایجاد تغییر شکل دائمی یا حتی تغییر در ساختار بلوری و ترکیب شیمیایی مواد شوند.

تنش ساده

گاهی اوقات، تنش‌های موجود در یک جسم را می‌توان با استفاده از یک مقدار عددی یا یک بردار (مقدار و جهت) بیان کرد. به این تنش‌ها، «تنش ساده» (Simple Stress) گفته می‌شود و کاربرد اصلی آن‌ها در طراحی‌های مهندسی است. تنش نرمال تک محوری، تنش برشی ساده و تنش نرمال همسانگرد، از انواع تنش‌های ساده هستند. در ادامه، به توضیح هر یک از این موارد خواهیم پرداخت.

تنش نرمال تک محوری

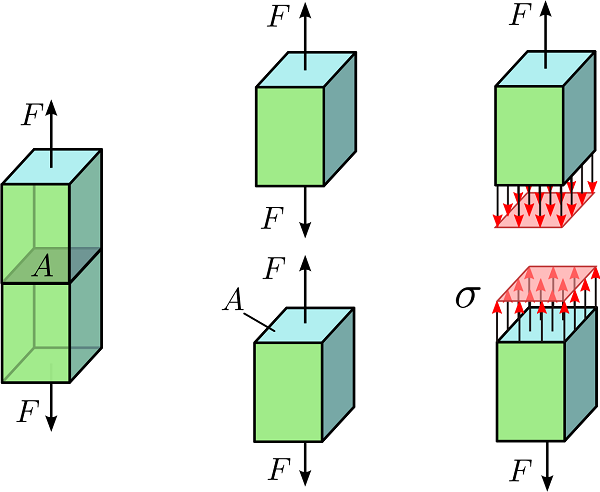
تنش نرمال تک محوری، یکی از متداول‌ترین الگوهای تنش ساده است. فرض کنید که یک میله مستقیم با سطح مقطع یکنواخت، مانند شکل زیر تحت دو نیروی کششی مخالف (با مقدار F) در جهت راستای خود قرار گرفته باشد. در صورت تعادل سیستم و قابل اغماض بودن وزن میله و همچنین عدم تغییر این شرایط در طی زمان، بخش بالایی هر مقطع عرضی باید بخش پایینی را توسط همان نیروی F در سراسر مقطع A تحت کشش قرار دهد. در این وضعیت می‌توان مقدار تنش داخل میله را به سادگی و تنها با تقسیم نیروی F بر سطح مقطع A محاسبه کرد:

$${\displaystyle \sigma ={\frac {F}{A}}}$$

اکنون، یک مقطع طولی از میله را به صورت موازی با محور نیرو در نظر بگیرید. در این وضعیت، هیچ نیرو و تنشی بین دو نیمه برش داده شده وجود نخواهد داشت. این نوع تنش، با عناوینی نظیر تنش نرمال (ساده)، تنش تک محوری و بخصوص تنش کششی (تک محوری یا ساده) شناخته می‌شود. اگر بارگذاری به صورت فشاری باشد، روش تحلیل یکسان خواهد بود اما علامت نیروی F و تنش σ تغییر خواهد کرد. به تنش در این حالت، تنش فشاری گفته می‌شود.

فیلم آموزش مقاومت مصالح 1 و 2 – مرور و حل مساله در فرادرس

کلیک کنید

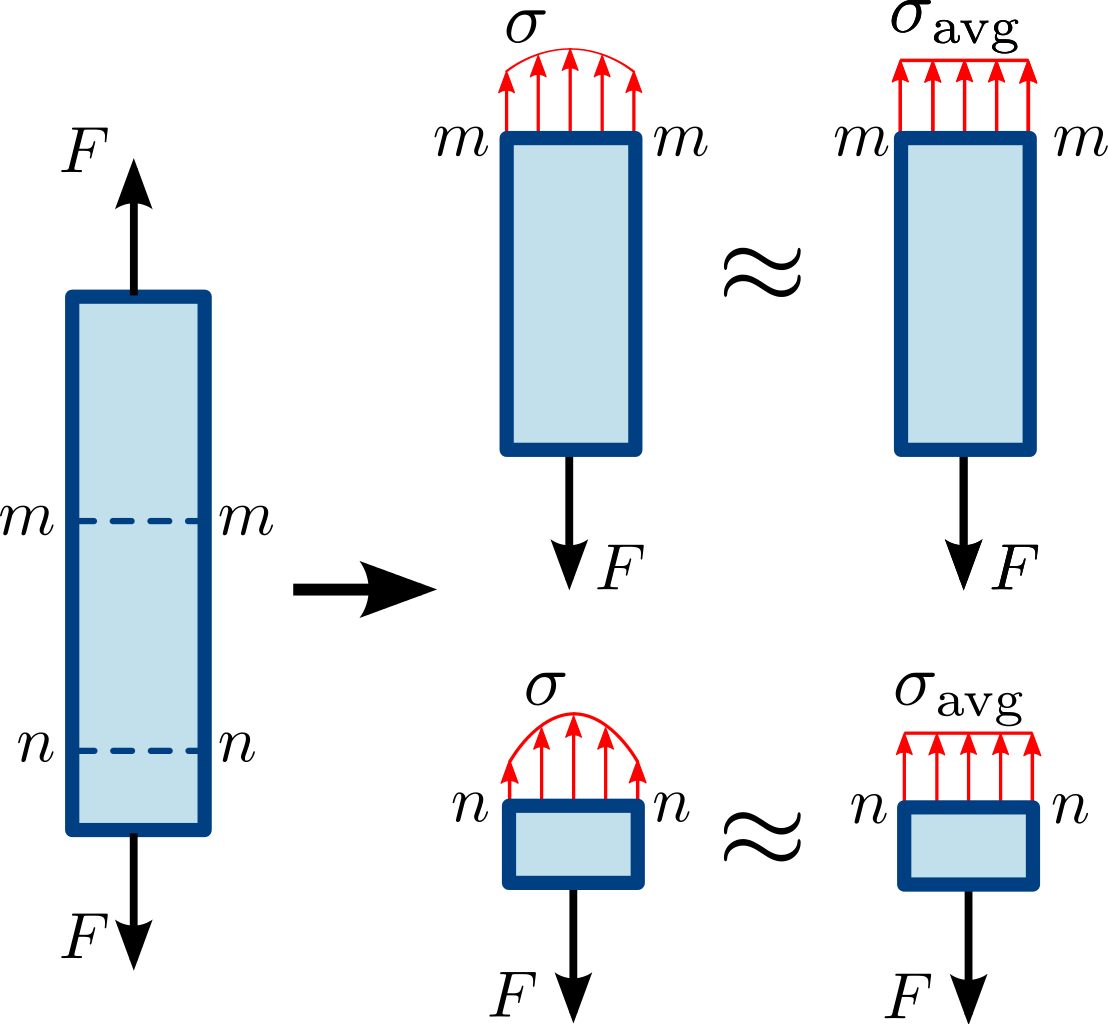
در تحلیل‌های بالا، فرض می‌شود که تنش بر روی تمام سطح مقطع به صورت یکنواخت توزیع شده است. از آنجایی که توزیع تنش در یک میله به نحوه ساخت و اتصال انتهای آن بستگی دارد، فرض یکنواخت بودن توزیع تنش همیشه صادق نیست. در چنین شرایطی، مقدار به دست آمده از فرمول σ=F/A، میانگین تنش را نشان خواهد داد که به آن «تنش مهندسی» (Engineering Stress) یا «تنش اسمی» (Nominal Stress) گفته می‌شود. اگر طول میله (L) چندین برابر قطر آن (D) باشد و هیچ عیب و نقص بزرگ یا تنش داخلی در آن وجود نداشته باشد، فرض توزیع یکنواخت تنش برای سطح مقطعی با فاصله زیاد (چند D) از هر دو انتهای میله صحیح خواهد بود (شکل زیر). این فرض به عنوان «اصل سنت ونانت» (Saint-Venant's Principle) شناخته می‌شود.

به غیر از اعمال نیروی کششی و فشاری در راستای محور جسم، تنش نرمال در شرایط دیگر نیز رخ می‌دهد. به عنوان مثال، اگر یک میله الاستیک با سطح مقطع یکنواخت و متقارن، در محل یکی از صفحات تقارن خود خم شود، «تنش خمشی» (Bending Stress) اعمال شده، به صورت نرمال (عمود بر سطح مقطع) خواهد بود. با این وجود، تنش بر روی سطح مقطع تغییر خواهد کرد. در این حالت، بخش خارجی سطح مقطع، تحت تنش کششی و بخش داخلی آن، تحت تنش فشاری قرار خواهد گرفت. یکی دیگر از انواع تنش نرمال، «تنش حلقوی» (Hoop Stress) است. این تنش در دیواره لوله‌های استوانه‌ای یا مخازنی پر شده با مایع تحت فشار رخ می‌دهد. معمولا تغییر شکل در این حالات می‌تواند در نتیجه انبساط گرمایی باشد.

تنش برشی ساده

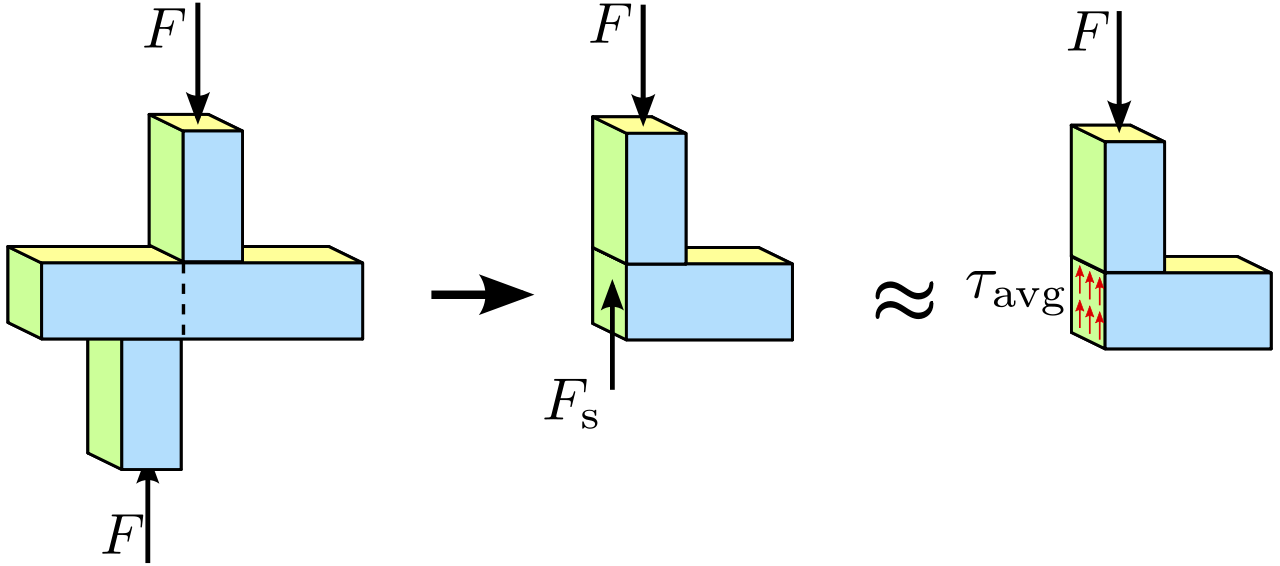
فرض کنید لایه ضخیم و یکنواختی از یک ماده الاستیک (مانند چسب یا لاستیک)، دو جسم سخت را به هم متصل کرده باشد و این دو جسم، در خلاف جهت یکدیگر و موازی با لایه به هم نیرو وارد کنند. در مثالی دیگر، مقطعی از یک میله فلزی نرم (مانند سیم برق) را در نظر بگیرید که به وسیله یک ابزار قیچی مانند (مانند سیم‌چین) برش داده می‌شود. در هر دو مثال بالا، سطح مقطع مورد بررسی تحت یکی از انواع تنش ساده با عنوان «تنش برشی ساده» (Simple Shear Stress) قرار می‌گیرد. اگر F مقدار نیروی اعمال شده و M سطح میانی لایه الاستیک باشد، بخشی از لایه در یک سمت M باید بخش دیگر را با نیروی F تحت کشش قرار دهد (مانند تنش نرمال). با فرض مشخص بودن جهت اعمال نیرو، تنش موجود بر روی سطح M به سادگی و تنها با تقسیم مقادیر نیرو بر مساحت سطح مقطع قابل محاسبه خواهد بود:

$$\tau ={\frac {F}{A}}$$

برخلاف تنش نرمال، جهت تنش برشی ساده موازی با سطح مقطع مورد بررسی است. برای تمامی سطوح عمود بر لایه (S)، برآیند نیروی داخلی و در نتیجه تنش موجود در راستای S صفر خواهد بود.

تنش همسانگرد

یکی دیگر از انواع تنش‌های ساده، «تنش همسانگرد» (Isotropic Stress) است. هنگامی که یک جسم در همه جهات خود تحت فشار یا کشش برابر قرار گیرد، تنش همسانگرد رخ خواهد داد. فرض کنید که سیالات یا گازهای درون یک محفظه بسته یا بخشی از این مواد در حالت سکون قرار گرفته باشند. در مورد دیگر، یک جسم مکعبی شکل الاستیک را در نظر بگیرید که به تمام شش وجهه آن، نیروی قائم فشاری یا کششی (F) وارد می‌شود (تمام نیروها با هم برابر هستند). در هر دو مثال بالا فرض می‌شود که مواد به صورت همگن و بدون تنش داخلی هستند. علاوه بر این، اثر جاذبه و دیگر نیروهای خارجی قابل اغماض است.

فیلم آموزش مقاومت مصالح 1 و 2 – مرور و حل مساله در فرادرس

کلیک کنید

در این شرایط، مقدار تنش بر روی تمامی مقاطع فرضی یکسان و جهت‌گیری آن به صورت عمود بر سطح خواهد بود. به این نوع تنش، تنش نرمال همسانگرد یا تنش همسانگرد گفته می‌شود. در صورت فشاری بودن تنش، به آن فشار هیدرو استاتیک یا فشار می‌گویند. با توجه به تعریف، گازها توانایی تحمل تنش‌های کششی را ندارند اما مایعات می‌توانند در شرایط خاص، مقدار قابل توجهی از تنش‌های کششی همسانگرد را تحمل کنند.

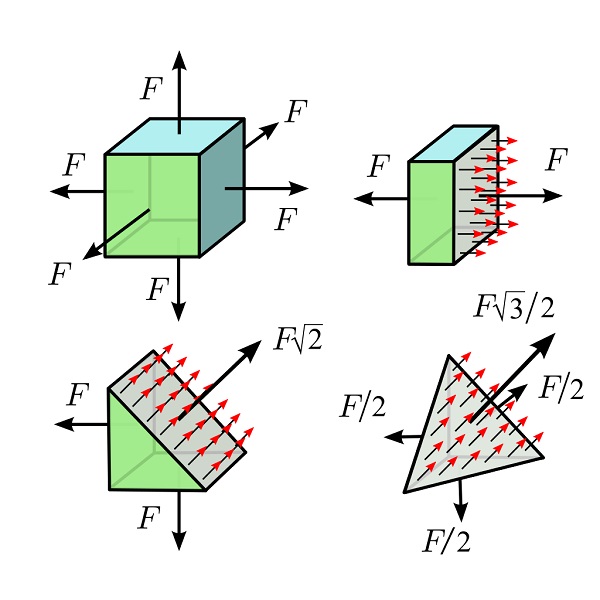
تصویر بالا، تنش کششی همسانگرد در مقاطع مختلف یک جسم مکعبی شکل را نشان می‌دهد. تمام سطوح این مکعب همگن، تحت نیروی کششی F قرار گرفته‌اند. مقدار نیروی وارده به هر یک از سطوح مکعب (مساحت A) با یکدیگر برابر است. نیروی وارد بر هر مقطع دلخواه (S) باید با نیروی وارد بر بخش دیگر مقطع در حالت تعادل باشد. برای هر یک از مقاطع، نیروی وارد شده به ترتیب برابر با F (بالا راست)، 2√F (پایین چپ) و 3/2√F (پایین راست ) و مساحت هر مقطع نیز به ترتیب A (بالا راست)، 2√A (پایین چپ) و 3/2√A (پایین راست) است. بنابراین، مقدار تنش بر روی S در هر سه مورد برابر با F/A خواهد بود.

تنش‌های استوانه‌ای

قطعاتی از قبیل چرخ‌ها، محورها، لوله‌ها و ستون‌ها که دارای تقارن چرخشی هستند، کاربردهای زیادی در مسائل مهندسی دارند. در اغلب موارد، الگوی توزیع تنش در این قطعات دارای تقارن چرخشی یا حتی استوانه‌ای است. در تحلیل «تنش‌های استوانه‌ای» (Cylinder Stresses) می‌توان از تقارن جسم برای کاهش ابعاد محدوده مورد بررسی و یا تانسور تنش بهره برد.

امیدواریم بخش اول این مقاله برایتان مفید واقع شده باشد.در بخش دوم به توضیح حالت تنش، تحلیل تنش و معیارهای اندازه‌گیری تنش خواهیم پرداخت. اگر به مطالعه موضوعات مشابه علاقه‌مند هستید، مطالب زیر را به شما پیشنهاد می‌کنیم:

• مجموعه آموزش های مهندسی عمران
• آموزش مقاومت مصالح
• مجموعه آموزش‌های دروس مهندسی مکانیک
• انبساط گرمایی -- به زبان ساده
• مجموعه مقالات آشنایی با مفاهیم مقاومت مصالح و خواص مکانیکی مواد

^^