رسم تابع چگالی احتمال دو بعدی با پایتون — راهنمای کاربردی

امروزه با توجه به حجم وسیع داده‌ها و اطلاعاتی که روزانه تولید و به کار گرفته می‌شوند، تجزیه و تحلیل آن‌ها امری مهم به حساب می‌آید. یکی از مراحل تحلیل داده‌ها در «داده‌کاوی» (Data Mining) مرحله «نمایش داده‌ها» (Data Visualization) است که یک روش برای توصیف رفتار پدیده‌ها براساس مشاهدات و اندازه‌های جمع‌آوری شده است. یکی از تکنیک‌های معمول برای این کار، رسم «نمودار فراوانی» یا «هیستوگرام» (Histogram) است. زمانی که فراوانی‌ها یا تعداد مشاهدات در هر گروه را به صورت درصدی در هیستوگرام نشان دهیم، در حقیقت یک نمودار چگالی را رسم کرده‌ایم. در این نوشتار با نحوه رسم تابع چگالی احتمال دو بعدی با پایتون آشنا می‌شویم و برای سه سری داده دو بُعدی، تابع توزیع احتمال را برآورد کرده و نمودار آن را رسم خواهیم کرد. در حقیقت این نمودارها باید به صورت سه بعدی باشند تا بتوانند رفتار دو متغیر تصادفی (مستقل یا وابسته) را براساس مقدار چگالی احتمال نشان دهند. به همین علت نیز در انتهای متن نمودارهای سه بُعدی را شاهد خواهید بود.

پیش از شروع و برای درک راحت‌تر این نوشتار، بهتر است مطلب رسم نمودار در پایتون با Matplotlib — راهنمای کاربردی و رسم نمودار داده ها در پایتون — راهنمای تخصصی را مطالعه کنید. همچنین خواندن نوشتارهای توزیع های آماری — مجموعه مقالات جامع وبلاگ فرادرس و توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها نیز خالی از لطف نیست.

رسم تابع چگالی احتمال دو بعدی با پایتون

معمولا برای بیان و توصیف رفتار پدیده‌های تصادفی از تابع احتمال (در حالت گسسته) یا تابع چگالی احتمال (در حالت پیوسته) استفاده می‌شود. در اینجا قصد داریم براساس داده‌های شبیه‌سازی شده، نمودار تابع چگالی داده‌های پیوسته را بوسیله «کرنل گوسی» (Gaussian Kernel) برآورد کرده و سپس ترسیم کنیم. در این بین از زبان برنامه‌نویسی پایتون و بعضی از توابع مربوط به کتابخانه Matplotlib استفاده خواهیم کرد.

فیلم آموزش تئوری احتمالات – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

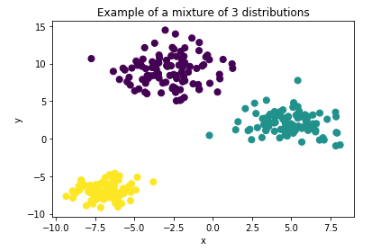
ابتدا به تولید ۳۰۰ مشاهده یا داده‌ها بوسیله شبیه‌سازی با تابع make_blobs می‌پردازیم. این تابع از توزیع نرمال چند متغیره آمیخته با میانگین و واریانس مشخص شده، داده تولید می‌کند. کدهای زیر به این منظور نوشته شده‌اند. واضح است که از هر گروه ۱۰۰ مشاهده ایجاد خواهد شد.

1import numpy as np
2import matplotlib.pyplot as plt
3import scipy.stats as st
4from sklearn.datasets import make_blobs
5n_components = 3
6X, truth = make_blobs(n_samples=300, centers=n_components, 
7                      cluster_std = [2, 1.5, 1], 
8                      random_state=42)
9plt.scatter(X[:, 0], X[:, 1], s=50, c = truth)
10plt.title(f"Example of a mixture of {n_components} distributions")
11plt.xlabel("x")
12plt.ylabel("y");

در انتها نیز نمودار نقطه‌ای (Dotplot) از این داده‌ها مشاهده می‌کنید. محور افقی و عمودی دو بعد داده‌ها را مشخص می‌کنند. مشخص است که گروه‌ها یا دسته‌های مجزایی از این نمونه‌ها تولید شده که البته واریانس متفاوتی نیز دارند. برای مثال واضح است که گروه یا دسته زرد رنگ، واریانس کوچکتری دارند در حالیکه گروه یا دسته بنفش، دارای واریانس بزرگتر و در نتیجه پراکندگی بیشتری هستند. متاسفانه چگالی احتمال یا فراوانی در این نمودار دیده نمی‌شود.

برای رسم نمودار تابع چگالی، احتیاج به برآورد تابع احتمال داریم. در ادامه، برآورد تابع چگالی این داده‌ها توسط روش کرنل گاوسی انجام خواهد شد. برای راحتی کار و نمایش مقدارها روی محورها، ابتدا مقدارها را برای هر بُعد استخراج کرده و سپس با استفاده از تابع np.mgrid و کرنل گاوسی در تابع np.reshape مقدار تابع چگالی برای داده‌های دو بعدی را تخمین می‌زنیم. ابتدا عمل تفکیک ابعاد داده‌ها را به کمک کد زیر انجام می‌دهیم.

1# Extract x and y
2x = X[:, 0]
3y = X[:, 1]
4# Define the borders
5deltaX = (max(x) - min(x))/10
6deltaY = (max(y) - min(y))/10
7xmin = min(x) - deltaX
8xmax = max(x) + deltaX
9ymin = min(y) - deltaY
10ymax = max(y) + deltaY
11print(xmin, xmax, ymin, ymax)
12# Create meshgrid
13xx, yy = np.mgrid[xmin:xmax:100j, ymin:ymax:100j]

حال که به داده‌های دو بُعدی دسترسی داریم لازم است که براساس آن‌ها تابع چگالی را با کتابخانه gaussian_kde تخمین بزنیم.

1positions = np.vstack([xx.ravel(), yy.ravel()])
2values = np.vstack([x, y])
3kernel = st.gaussian_kde(values)
4f = np.reshape(kernel(positions).T, xx.shape)

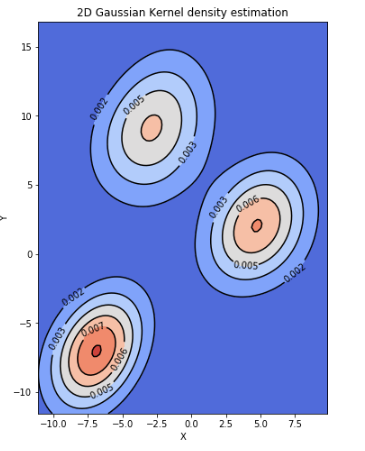
برای نمایش تابع چگالی حاصل از برآورد کرنل از نمودار کانتور (Contout Plot) استفاده می‌کنیم. کد زیر به این منظور نوشته شده است.

1fig = plt.figure(figsize=(8,8))
2ax = fig.gca()
3ax.set_xlim(xmin, xmax)
4ax.set_ylim(ymin, ymax)
5cfset = ax.contourf(xx, yy, f, cmap='coolwarm')
6ax.imshow(np.rot90(f), cmap='coolwarm', extent=[xmin, xmax, ymin, ymax])
7cset = ax.contour(xx, yy, f, colors='k')
8ax.clabel(cset, inline=1, fontsize=10)
9ax.set_xlabel('X')
10ax.set_ylabel('Y')
11plt.title('2D Gaussian Kernel density estimation')

در نتیجه نموداری به صورت زیر ظاهر خواهد شد.

البته برای نمایش نمودار به صورتی دیگر از quadcontour استفاده می‌کنیم که توسط تابع cset مشخص می‌شود. برای دسترسی به هر قطعه از نمودار کانتور از متغیر allsegs بهره می‌گیریم که براساس اندیس $$j$$ امکان دسترسی به هر لایه از نمودار کانتور را فراهم می‌کند. کدی که در زیر مشاهده می‌کنید، نمودار کانتوری را رسم می‌کند که هر لایه از آن در راهنمای نمودار ظاهر می‌شود.

1plt.figure(figsize=(8,8))
2for j in range(len(cset.allsegs)):
3    for ii, seg in enumerate(cset.allsegs[j]):
4        plt.plot(seg[:,0], seg[:,1], '.-', label=f'Cluster{j}, level{ii}')
5plt.legend()

نمودار حاصل از اجرای این کد به صورت زیر خواهد بود.

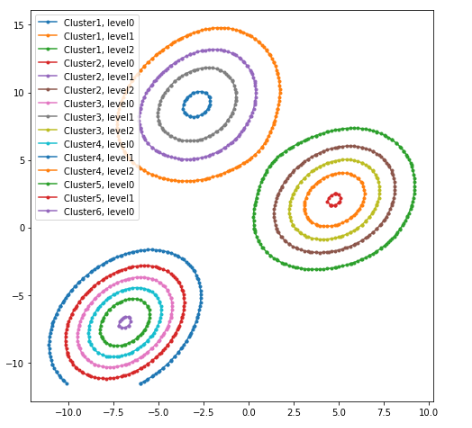
در گام بعدی با استفاده از یک نمودار سه بُعدی نمودار تابع چگالی برای داده‌های تولید شده ترسیم می‌کنیم. در این حالت از آنجایی که برای برآورد تابع چگالی کرنل گاوسی را به کار گرفته‌ایم، نمودار حاصل را «برآورد کرنل تابع چگالی» (Kernel Density Estimation) یا به اختصار KDE می‌نامیم. در اینجا از تابع surface مربوط به کتابخانه matplotlib استفاده کرده‌ایم.

1fig = plt.figure(figsize=(13, 7))
2ax = plt.axes(projection='3d')
3surf = ax.plot_surface(xx, yy, f, rstride=1, cstride=1, cmap='coolwarm', edgecolor='none')
4ax.set_xlabel('x')
5ax.set_ylabel('y')
6ax.set_zlabel('PDF')
7ax.set_title('Surface plot of Gaussian 2D KDE')
8fig.colorbar(surf, shrink=0.5, aspect=5) # add color bar indicating the PDF
9ax.view_init(60, 35)

نمودار ترسیم شده توسط این کد در زیر دیده می‌‌شود.

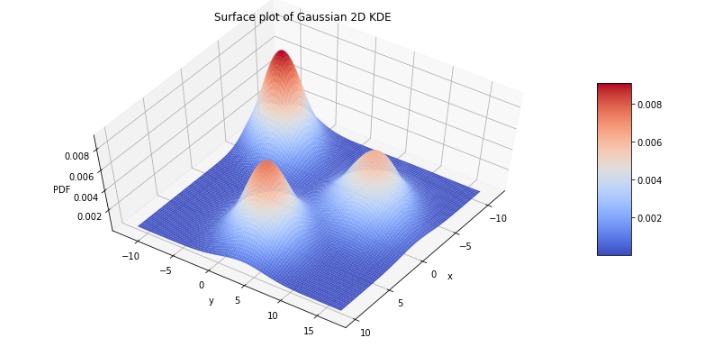
واضح است که در این نمودار، محور X و Y مربوط به دو بعد داده‌ها هستند و محور Z نیز همان تابع چگالی را نشان می‌دهد. از آنجایی که داده‌ها از توزیع نرمال تولید شده بودند، انتظار داریم که نمودار تابع چگالی آمیخته نیز به صورت سه نمودار توزیع نرمال دو متغیره (‌به حالت کله قند) درآید که البته این اتفاق هم افتاده است.

فیلم آموزش آزمون های نیکویی برازش با نرم افزار EasyFit در فرادرس

کلیک کنید

برای مقایسه بهتر و دیدی متفاوت از نمودار بعدی از «خطوط سه بعدی» (Wireframe Plot) استفاده کرده‌ایم. برای انجام این کار از دستورات زیر کمک گرفته‌ایم.

1fig = plt.figure(figsize=(13, 7))
2ax = plt.axes(projection='3d')
3w = ax.plot_wireframe(xx, yy, f)
4ax.set_xlabel('x')
5ax.set_ylabel('y')
6ax.set_zlabel('PDF')
7ax.set_title('Wireframe plot of Gaussian 2D KDE');

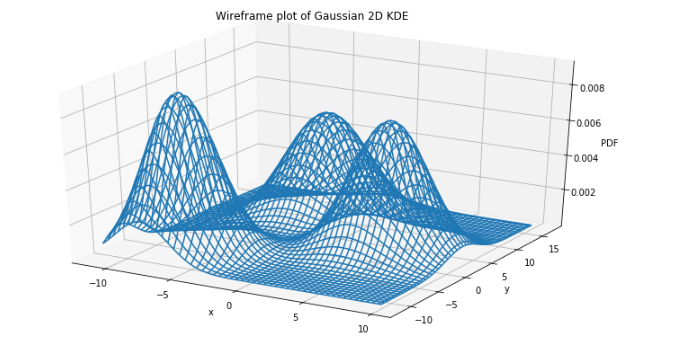
در انتها نیز با استفاده از یک نمودار گرمایی یا حرارتی (Heatmap) نموداری شبیه هیستوگرام دو بُعدی را ترسیم می‌کنیم. واضح است که در اینجا رنگ زرد نشانگر ارتفاع بیشتر در نمودار است. کد زیر نمودار مورد نظر را برایمان ترسیم می‌کند.

1h =plt.hist2d(x, y)
2plt.colorbar(h[3])

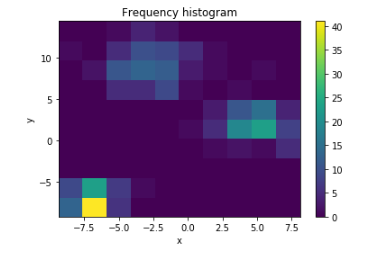
اگر مطلب بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار و احتمالات
• آموزش نمایش داده‌ها و ترسیم نمودار در اکسل
• مجموعه آموزش‌های نرم‌افزار آماری SPSS
• مجموعه آموزش‌های برنامه‌نویسی متلب (MATLAB)
• هیستوگرام (Histogram) و نمودارهای چگالی — راهنمای بصری سازی داده‌های تک‌ بُعدی در پایتون
• رسم نمودار داده ها در پایتون — راهنمای تخصصی

^^