جستجوی فیبوناچی (Fibonacci Search) – به زبان ساده

در علوم کامپیوتر، «الگوریتم جستجو» (Search Algorithm)، الگوریتمی است که «مساله جستجو» (Search Problem) را حل می‌کند. در واقع، اطلاعات ذخیره شده درون ساختار داده، فضای جستجو یا دامنه مساله، با مقادیر گسسته یا پیوسته را بازیابی می‌کند. روش‌های جستجوی گوناگونی وجود دارند که از این جمله می‌توان به «جستجوی دودویی» (Binary Search)، «جستجوی درون‌یابی» (Interpolation Search)، «جستجوی پرشی» (Jump Search) و «جستجوی فیبوناچی» (Fibonacci Search) اشاره کرد. در این مطلب، الگوریتم جستجوی فیبوناچی مورد بررسی قرار گرفته و پیاده‌سازی آن با زبان‌های «سی» (C)، «جاوا» (Java)، «پایتون» (Python)، «سی‌شارپ» (#C) و «پی‌اچ‌پی» (PHP) انجام شده است.

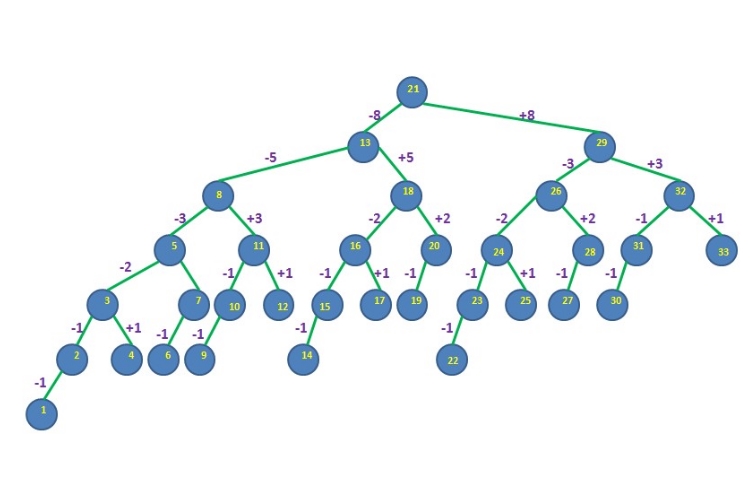
جستجوی فیبوناچی

یک آرایه مرتب شده []arr در اندازه n داده شده است و قرار است عنصر x در آن جستجو شود. «جستجوی فیبوناچی» (Fibonacci Search) اندیس x را در صورت وجود باز می‌گرداند و در صورتی که این عنصر در آرایه وجود نداشته باشد، اندیس ۱- را باز می‌گرداند.

فیلم آموزش درخت جستجوی دودویی (AVL) در ساختمان داده ها (رایگان) در فرادرس

کلیک کنید

مثال زیر در این راستا قابل توجه است.

Input:  arr[] = {2, 3, 4, 10, 40}, x = 10
Output:  3
Element x is present at index 3.

Input:  arr[] = {2, 3, 4, 10, 40}, x = 11
Output:  -1
Element x is not present.

جستجوی فیبوناچی یک روش جستجوی «مبتنی بر مقایسه» (Comparison-Based) است که از اعداد فیبوناچی برای جستجوی یک عنصر در آرایه مرتب شده استفاده می‌کند.

شباهت‌های روش جستجوی فیبوناچی با جستجوی دودویی

• برای آرایه‌های مرتب شده کار می‌کند.
• یک الگوریتم «تقسیم و حل» (Divide and Conquer) است.
• دارای پیچیدگی زمانی از مرتبه Log n است.

فیلم آموزش روش حریصانه در طراحی الگوریتم - مرور تست کنکور ارشد (رایگان) در فرادرس

کلیک کنید

تفاوت‌ها با جستجوی دودویی

• جستجوی فیبوناچی یک آرایه داده شده را به بخش‌های غیر هم‌اندازه تقسیم می‌کند.
• جستجوی دودویی از عملگر تقسیم برای تقسیم بازه (Range) استفاده می‌کند. جستجوی فیبوناچی از / استفاده نمی‌کند، اما از عملگرهای + و - استفاده می‌کند. عملگرد تقسیم در برخی از «واحدهای پردازش مرکزی» (Central Processing Unit | CPU) دارای هزینه محاسباتی زیاد است.
• جستجوی فیبوناچی عناصر نسبتا نزدیک‌تر را در گام‌های متوالی دنبال می‌کند. بنابراین، هنگامی که آرایه ورودی به اندازه‌ای بزرگ باشد که نتواند در کش CPU یا حتی در «رم» (RAM) برازش پیدا کند، جستجوی فیبوناچی مفید واقع می‌شود.

پیش‌زمینه

اعداد فیبوناچی به صورت بازگشتی F(n) = F(n-1) + F(n-2), F(0) = 0, F(1) = 1 تعریف می‌شوند. اولین اعداد فیبوناچی، 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 و 144 هستند و این دنباله به همین صورت ادامه دارد.

مشاهدات

مشاهده زیر برای محدود کردن بازه مورد استفاده قرار می‌گیرد و بنابراین، پیچیدگی زمانی از درجه ((O(log(n است.

الگوریتم جستجوی فیبوناچی

فرض می‌شود عنصری که قرار است جستجو شود x است. ایده آن است که ابتدا کوچک‌ترین عدد فیبوناچی که بزرگ‌تر یا مساوی طول (اندازه) آرایه کنونی است یافته شود. عدد فیبوناچی یافت شده، در اینجا fib در نظر گرفته می‌شود. از (m-2)اُمین عدد فیبوناچی به عنوان اندیس استفاده می‌شود (اگر یک اندیس معتبر باشد).

فیلم آموزش ساختمان داده ها – مرور و تست کنکور ارشد در فرادرس

کلیک کنید

فرض می‌شود (m-2)‌اُمین عدد فیبوناچی i باشد، [arr[i با x مقایسه می‌شود، اگر مقدار آرایه در اندیس بیان شده با x برابر بود، i بازگردانده می‌شود؛ اگر x بزرگ‌تر بود، برای زیر آرایه بعد از i این مورد تکرار می‌شود و در غیر این صورت، (x کوچک‌تر بود) برای زیر آرایه پیش از i تکرار انجام می‌شود. در ادامه، الگوریتم کامل آورده شده است.

فرض می‌شود آرایه [arr[0..n-1، آرایه ورودی و عنصری که جستجو می‌شود x است.

1. کوچک‌ترین عدد فیبوناچی بزرگ‌تر یا مساوی با n را پیدا کن. فرض می‌شود این عدد fibM [یعنی m‌اُمین عدد فیبوناچی] است. دو عدد فیبوناچی قبلی fibMm1 (یعنی (m-1)اُمین عدد فیبوناچی) و fibMm2 (یعنی (m-2)اُمین عدد فیبوناچی هستند).
2. در حالی که آرایه دارای عناصری است که باید وارسی شوند:
   1. x را با آخرین عنصر از طیف پوشش داده شده با fibMm2 مقایسه کن.
   2. اگر x مطابق بود، اندیس را بازگردان.
   3. در غیر این صورت اگر x کمتر از عنصر است، سه متغیر فیبوناچی را دو تا فیبوناچی عقب ببر؛ این کار با هدف حذف تقریبا دو سوم باقیمانده از آرایه مورد استفاده قرار می‌گیرد.
   4. در غیر این صورت، x بزرگ‌تر از عنصر است؛ سه متغیر فیبوناچی را یک فیبوناچی عقب ببر، نقطه شروع را با مقدار اندیس بازنشانی کن. انجام این کارها موجب حذف یک سوم پیش روی باقیمانده از آرایه می‌شود.
3.  از آنجا که ممکن است تنها یک عنصر برای مقایسه باقی مانده باشد، بررسی کن که fibMm1 برابر با ۱ است یا خیر. اگر پاسخ بلی بود، x را با عنصر باقیمانده مقایسه کن و در صورت مطابقت داشتن، اندیس را باز گردان.

پیاده‌سازی جستجوی فیبوناچی در C

پیاده‌سازی جستجوی فیبوناچی در جاوا

پیاده‌سازی جستجوی فیبوناچی در پایتون ۳

پیاده‌سازی جستجوی فیبوناچی در #C

پیاده‌سازی جستجوی فیبوناچی در PHP

خروجی:

Found at index: 8

مثال از الگوریتم جستجوی فیبوناچی

برای درک بهتر الگوریتم، مثال زیر قابل توجه است.

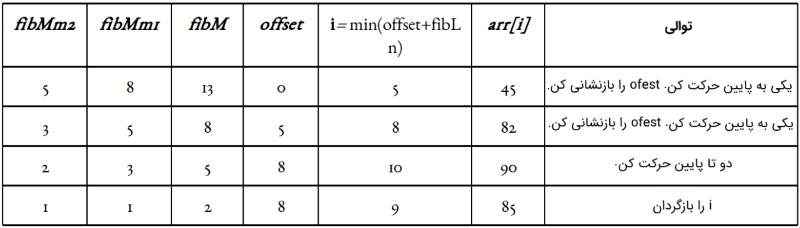
فرضیه: اندیس‌گذاری از ۱ شروع می‌شود. عنصر هدف ۸۵ و طول آرایه n=11 است.

• کوچک‌ترین عدد فیبوناچی بزرگ‌تر یا مساوی ۱۱، برابر با ۱۳ است. همانطور که در تصویر مشهود است، fibMm1 = 8 ،fibMm2 = 5 و fibM = 13 است.
• دیگر جزئیات پیاده‌سازی متغیر اُفسِت (مقداردهی اولیه آن با صفر انجام شده) عبارتند از اینکه، این متغیر طیفی که حذف شده را مشخص می‌کند که از جلو آغاز می‌شود و همچنین، متغیر لحظه به لحظه به روز رسانی می‌شود.

اکنون با توجه به اینکه مقدار افست برابر با اندیس است و همه اندیس‌های شامل آن و مقادیر زیر آن حذف شده‌اند، تنها کاری که می‌تواند معنادار باشد افزودن چیزی به آن است. از آنجا که fibMm2 تقریبا یک سوم از آرایه را نشانه‌گذاری می‌کند و در عین حال اندیس‌هایی که علامت‌گذاری می‌کند اندیس‌های معتبری هستند، می‌توان fibMm2 را به offset افزود و عنصر در اندیس  (i = min(offset + fibMm2, n را بررسی کرد.

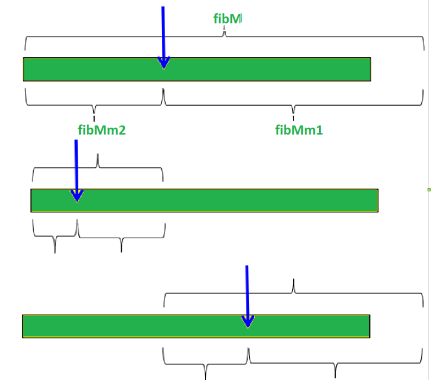
بصری‌سازی:

تحلیل پیچیدگی

بدترین حالت هنگامی است که هدف در ۲/۳ بزرگ‌تر آرایه باشد و فرایند جستجو تا پیدا کردن آن ادامه پیدا کند. به بیان دیگر، هر بار ۱/۳ کوچک‌تر آرایه حذف می‌شود.

فراخوانی یک بار برای n، بار دیگر برای $$(2/3) n$$، سپس برای $$(4/9) n$$ و به همین صورت انجام می‌شود. این مورد را می‌توان به صورت زیر در نظر گرفت.

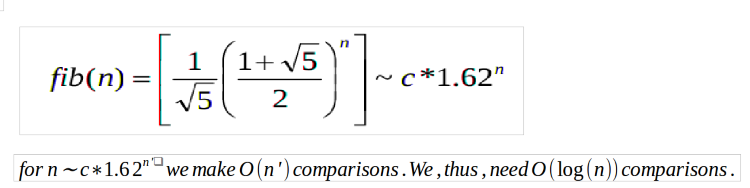
اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌ نویسی
• آموزش ساختمان داده‌ها
• مجموعه آموزش ساختمان داده و طراحی الگوریتم
• زبان برنامه‌نویسی پایتون (Python) — از صفر تا صد
• ده زبان برنامه‌نویسی که باید در سال 13۹۸ یاد بگیرید
• آموزش ساختمان داده — مجموعه مقالات جامع وبلاگ فرادرس
• ساختمان داده (Data Structure) — راهنمای جامع و کاربردی

^^