آشنایی با تبدیلات تنش — مبانی مقاومت مصالح

حالت کلی تنش در هر نقطه‌ای از یک جسم تحت بارگذاری را می‌توان با استفاده از سه تنش نرمال (یک تنش در هر راستا) و شش تنش برشی (دو تنش در هر راستا) نشان داد. اندیس‌های موجود در کنار نام هر یک از تنش‌های نرمال (σ)، نشان دهنده راستای آن تنش در دستگاه مختصات است. در کنار نام تنش‌های برشی نیز اندیس‌هایی وجود دارند؛ با این تفاوت که برخلاف نام‌گذاری در تنش‌های نرمال، این اندیس‌های تنش‌های برشی دارای دو مؤلفه هستند. مؤلفه اول، راستای سطح عمود بر تنش و مؤلفه دوم، راستای تنش در دستگاه مختصات را مشخص می‌کند.

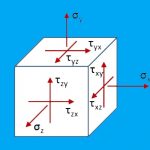
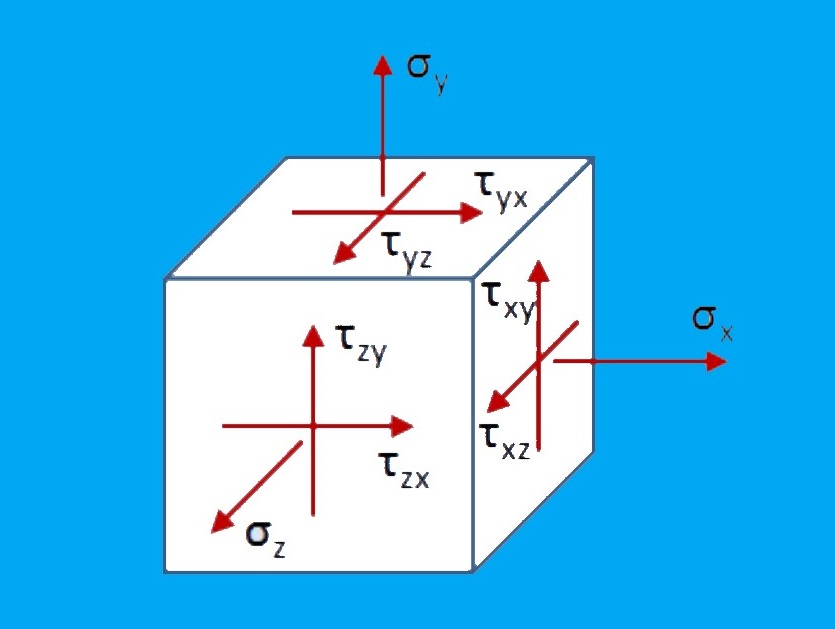
عموماً، تنش‌های موجود در یک راستا هنگامی صفر می‌شوند که حالت کلی تنش بر روی یک صفحه منفرد اعمال شده باشد (شکل زیر). به این حالت، تنش صفحه‌ای گفته می‌شود. تنش صفحه‌ای، در صفحات نازک و همچنین سطوح خارجی تمام سازه‌های تحت بارگذاری رخ می‌دهد. از آنجایی که تنش خمشی و پیچشی، در سطح اجسام به حداکثر مقدار خود می‌رسند، تنش‌های صفحه‌ای معمولاً به عنوان مهم‌ترین تنش‌های موجود در محاسبات به حساب می‌آیند.

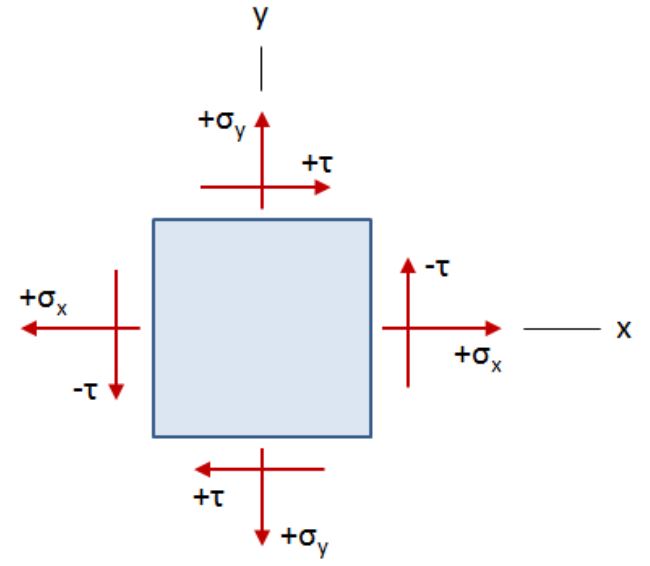
در شکل بالا، σ_x و σ_y، تنش‌های نرمال و τ، تنش برشی هستند. در این حالت، وضعیت تنش‌ها به گونه‌ای است که نقطه مورد نظر در حالت تعادل استاتیکی قرار داشته باشد. از آنجایی که مقدار تمام تنش‌های برشی با هم برابر است، اندیس‌های آن‌ها به منظور ساده‌سازی حذف شده‌اند.

فیلم آموزش مقاومت مصالح ۲ + مفاهیم کلیدی در فرادرس

کلیک کنید

البته، توجه داشته باشید که علامت تنش‌های هم‌راستا با محور x، مثبت و تنش‌های هم‌راستا با محور y، منفی خواهد بود.

قواعد علامت‌گذاری صحیح، به گونه‌ای است که در شکل بالا نشان داده شده. برای تنش‌های نرمال، علامت تنش کششی، مثبت و علامت تنش فشاری، منفی در نظر گرفته می‌شود. برای تنش‌های برشی، علامت تنش در جهت عقربه‌های ساعت، مثبت و برخلاف جهت عقربه‌های ساعت، منفی خواهد بود.

اگر مقدار تنش‌های نشان داده شده در شکل بالا مشخص باشد، می‌توان تنش‌های نرمال و برشی صفحه دوران یافته با زاویه θ (نسبت به افق) را تعیین کرد. با استفاده معادلات تبدیل در جدول زیر، مقادیر تنش‌های نرمال و برشی این صفحه دوران یافته به دست می‌آیند.

تنش نرمال: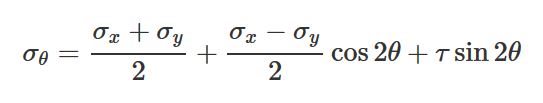
تنش برشی:

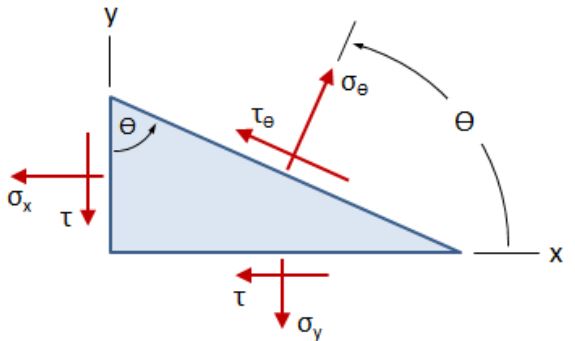
توجه داشته باشید که در شکل بالا، زاویه θ، نسب به محور x تعیین می‌شود. به علاوه، مقدار مثبت برای این زاویه، در جهت خلاف عقربه‌های ساعت است.

در هر نقطه از ماده، زوایایی را می‌توان یافت که تنش‌های نرمال و برشی صفحه در آن‌ها به مقادیر ماکسیمم و مینیمم خود می‌رسند. به تنش‌های نرمال ماکسیمم و مینیمم، تنش‌های اصلی گفته می‌شود. تنش‌های برشی ماکسیمم و مینیمم را نیز تنش‌های برشی حداکثری می‌گویند. با مشتق‌گیری از معادلات تبدیل (نسبت به θ) و برابر قرار دادن آن‌ها با صفر، مقدار زوایای تنش‌های اصلی و برشی به صورت زیر به دست می‌آیند.

زوایای تنش اصلی: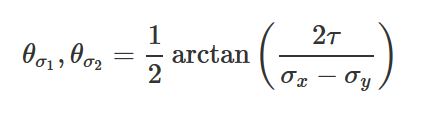
زوایای تنش برشی حداکثری: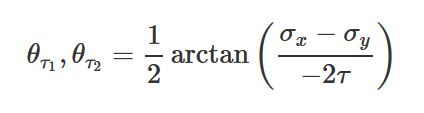

اگر زوایای بالا را در معادلات تبدیل جایگذاری کنیم، مقادیر تنش‌های اصلی و تنش‌های برشی حداکثری به صورت زیر خواهند بود:

تنش‌های اصلی: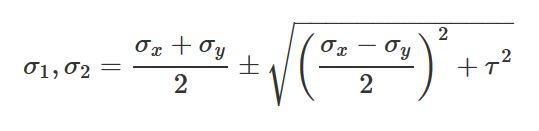
تنش‌های برشی حداکثری: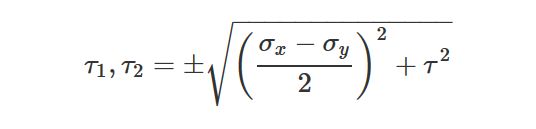

با بررسی معادلات مرتبط با تنش‌های اصلی و تنش‌های برشی حداکثری، می‌توان به نکات زیر پی برد:

• زوایایی که در آن‌ها تنش‌های اصلی رخ می‌دهد، با هم 90 درجه اختلاف دارند.
• محلی که تنش اصلی وجود داشته باشد، مقدار تنش برشی صفر خواهد بود.
• زوایایی که در آن‌ها تنش‌های برشی حداکثری رخ می‌دهد، 45 درجه با زوایای تنش‌های اصلی اختلاف دارند.
• تنش‌های برشی حداکثری، دارای دو تنش نرمال برابر با معادله 2/(σ_x + σ_y) هستند.

معادلات زیر در محاسبات تنش‌های اصلی و حداکثری کاربرد زیادی دارند:

جمع تنش‌های نرمال، مقدار ثابتی است.
تنش برشی حداکثر، برابر است با نصف تفاضل تنش‌های اصلی.

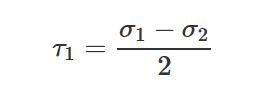امیدواریم این مطلب برایتان مفید واقع شده باشد. اگر به دنبال آموزش‌های مشابهی هستید، مطالب زیر را به شما پیشنهاد می‌کنیم:

• مجموعه آموزش های مهندسی عمران
• آموزش مقاومت مصالح
• مجموعه آموزش‌های دروس مهندسی مکانیک
• آموزش تنش و کرنش بارگذاری محوری در مقاومت مصالح
• مجموعه مقالات آشنایی با مفاهیم مقاومت مصالح و خواص مکانیکی مواد

^^