آینه مقعر در فیزیک — به زبان ساده

در آموزش‌های قبلی مجله فرادرس، درباره آینه تخت در فیزیک بحث کردیم. در این آموزش، به بررسی آینه مقعر یا کاو می‌پردازیم.

آینه‌های کروی

بیشتر ما از دیدن تصویرهای عجیب و غریب در آینه‌های منحنی شگفت‌زده شده‌ایم. یک نوع از آینه‌های منحنی، «آینه‌های کروی» (Spherical Mirrors) هستند. این آینه‌ها، بخشی از سطح یک کره هستند.

هنگامی که سطح داخلی آینه جیوه اندود باشد، آینه محدب یا «کوژ» (Convex Mirrors) تشکیل می‌شود. به عبارت دیگر در آینه کوژ یا محدب، سطح خارجی کره انعکاس دهنده نور یا «سطح انعکاس دهنده» (Reflecting Surface) است. به همین ترتیب هنگامی که سطح خارجی آینه جیوه اندود باشد، آینه مقعر یا «کاو» (Concave Mirrors) تشکیل می‌شود. به عبارت دیگر در آینه کاو یا مقعر سطح داخلی کره، انعکاس دهنده نور یا سطح انعکاس دهنده است.

تقارن یکی از اصول اساسی در بسیاری از قطعات نوری مثل آینه‌ها و لنزها است. آینه کروی با بریدن قطعه‌ای از کره و نقره یا جیوه اندود کردن داخل یا خارج کره، تشکیل می‌شود.

محور تقارن برای المان‌های نوری، معمولا به نام «محور اصلی» (Principal Axis) یا «محور نوری» (Optical Axis) شناخته می‌شود. در یک آینه کروی، محور نوری از «مرکز انحنا» (Center of Curvature) و «رأس آینه» (Vertex) عبور می‌کند. در شکل زیر، یک آینه کروی و مرکز انحنای آن نشان داده شده است:

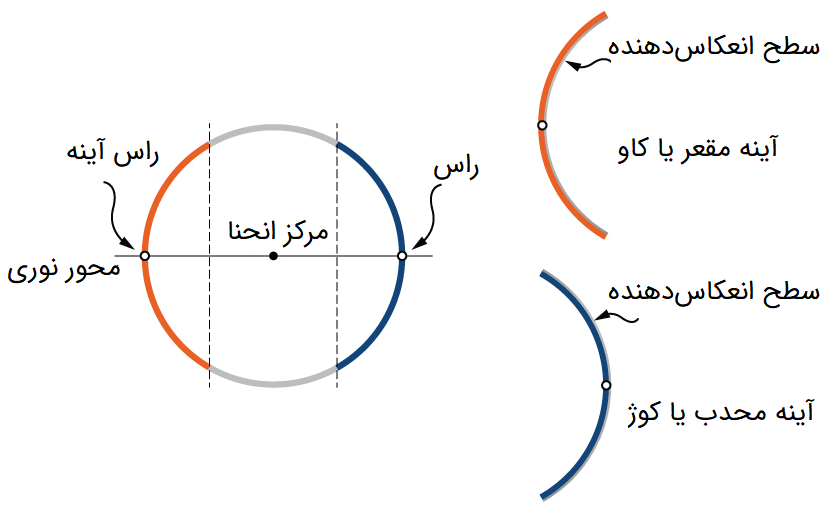
حال یک آینه سهموی را در نظر بگیرید. یک دسته پرتو به موازات محور نوری، به آینه سهموی تابیده می‌شود. این مسئله در شکل زیر نشان داده شده است:

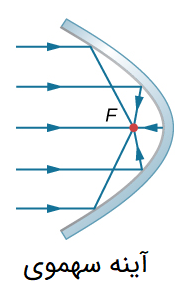
طبق قانون انعکاس، پرتوها پس از بازتاب در یک نقطه به هم می‌رسند که به نقطه کانونی آینه نامیده می‌شود.

در شکل زیر، یک آینه کروی نشان داده شده است:

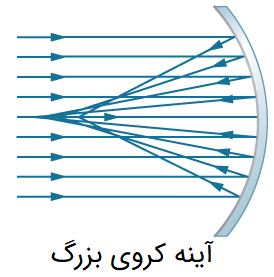
فرض می‌شود که ابعاد این آینه نسبت به شعاع انحنای آن، بسیار بزرگتر است. در این آینه، همه پرتوها از یک نقطه عبور نمی‌کنند. پس این آینه، یک نقطه کانونی مشخص ندارد. این پدیده، «انحراف کروی» (Spherical Aberration) نام دارد. به دلیل پدیده انحراف کروی، تصویر تشکیل شده از این نوع آینه‌ها، مات است.

شکل زیر یک آینه کروی را نشان می‌دهد که در آن، ابعاد آینه بسیار کوچکتر از شعاع انحنای کره آینه است:

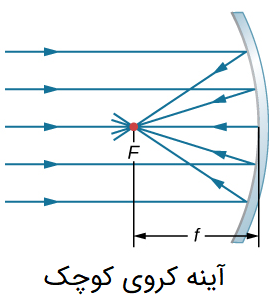
این آینه، تقریب مناسبی از آینه سهموی است. بنابراین پرتوهای موازی با محور نوری آينه، پس از برخورد به آینه و بازتاب از آن به یک نقطه کانونی مشخص می‌رسند. «فاصله کانونی» (Focal Length)، فاصله‌ای است که روی محور اصلی آینه اندازه‌گیری می‌شود و برابر با فاصله بین نقطه کانونی تا آینه است.

آینه‌های کروی در حالت کلی، یک مرکز انحنا، یک شعاع انحنا و یک محور اصلی دارند. محور اصلی از مرکز انحنای کره و مرکز آینه می‌گذرد. در آینه‌های کروی، تمامی پرتوها از یک نقطه واگرا یا در یک نقطه همگرا می‌شوند. اگر پرتوهای برخوردی به آینه به موازات محور اصلی به آن تابانده شوند، پس از بازتاب از یک نقطه عبور می‌کنند. این نقطه، «نقطه کانونی» (Focal Point) نام دارد. فاصله بین نقطه کانونی و مرکز تقارن آینه، «فاصله کانونی» (Focal Length) نامیده می‌شود.

محل نقطه کانونی در آینه‌های مقعر یا کاو، جلوی آینه و در آینه‌های محدب یا کوژ، پشت آینه است.

آینه مقعر یا کاو

شکل زیر را در نظر بگیرید:

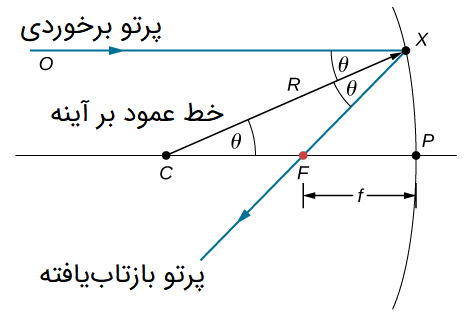
در این شکل، $$C$$ مرکز انحنای آینه و $$f$$ نقطه کانونی آن است. حال می‌خواهیم برای آینه‌های مقعر یا کاو، یک رابطه بین فاصله کانونی آینه و شعاع انحنای آینه به دست آوریم.

مطابق شکل، یک پرتو تکی به آینه کروی مقعر برخورد می‌کند و سپس بازتاب می‌یابد. پرتو برخوردی، با محور نوری آینه موازی است. این پرتو پس از بازتاب، محور نوری آینه را در نقطه کانونی آن قطع می‌کند. به یاد داشته باشید که همه پرتوهای برخوردی موازی محور اصلی آینه، هنگام بازتاب از نقطه کانونی عبور می‌کنند. در این شکل برای سادگی، فقط یک پرتو نشان داده شده است. فاصله کانونی ($$FP$$) به صورت خلاصه با $$f$$ نشان داده می‌شود. شعاع انحنای آینه نیز $$R$$ است. مطابق شکل، شعاع انحنای آینه برابر است با:

$$R = CF + FP$$
معادله (۱)

طبق قانون بازتاب، زاویه‌های $$\angle OXC$$ ‌و $$\angle CXF$$ با یکدیگر برابر هستند. از آنجا که پرتو برخوردی با محور نوری آینه موازی است، زاویه‌های $$\angle OXC$$ و $$\angle XCP$$ نیز با یکدیگر برابرند. بنابراین، مثلث $$CXF$$ یک مثلث متساوی‌الساقین است. در این مثلث، داریم:

$$CF=FX$$
معادله (۲)

اگر زاویه $$\theta$$ بسیار کوچک باشد، می‌توان نوشت:

 $$\sin θ≈ θ$$
معادله (۳)

معادله (۳) با نام «تقریب زاویه کوچک» (Small Angle Approximation) نیز شناخته می‌شود. به این ترتیب داریم:

 $$FX≈FP \, \, \, , \, \, \, CF≈FP$$
معادله (۴)

با جایگزینی معادله (۴) در معادله (۱)، خواهیم داشت:

$$\begin{align} R &=CF+FP \nonumber \\[5pt] &=FP+FP \nonumber \\[5pt] &=2FP\nonumber \\[5pt] &=2f \end{align}$$

به عبارت دیگر، با استفاده از تقریب زاویه کوچک می‌توان گفت که فاصله کانونی آینه مقعر کروی ($$f$$) با نصف شعاع انحنای آن ($$R$$)، برابر است. پس داریم:

$$f=\frac{R}{2}.$$
معادله (۵)

تقریب زاویه کوچک را «تقریب پیرامحوری» (Paraxial Approximation) نیز می‌نامند. فرض می‌شود که این تقریب، همواره معتبر است. اگر همه پرتوها در امتداد محور باشند، زاویه بین آنها و محور نوری کوچک است و فاصله آنها از محور نوری، کمتر از شعاع انحنای آینه است. در این حالت زوایای $$\theta$$ کوچک هستند. بنابراین:

$$\sin θ≈ \tan θ≈ θ.$$
معادله (۶)

در شکل (5)، مسیر پرتو نور موازی با محور اصلی رسم شده است. در واقعیت، پرتوهای نور با فاصله‌های مختلف از محور اصلی و زاویه‌های مختلف به آینه برخورد می‌کنند. پرتوهایی که با محور اصلی آینه تقریبا موازی هستند، زاویه برخورد کوچکی دارند. به این پرتوها، پرتوهای موازی گفته می‌شود. پرتوهای موازی پس از برخورد به آینه و بازتاب از آن، از نقطه کانونی آینه می‌گذرند.

پرتوهایی که نسبت به محور اصلی آینه زاویه دارند، دقیقا در نقطه کانونی همگرا نمی‌شوند. بنابراین فقط برای پرتوهای موازی، فاصله کانونی به اندازه نصف فاصله مرکز انحنا از مرکز آینه است.

همانطور که بیان شد،‌ این حقیقت که پرتوهای غیرموازی با محور اصلی از نقطه کانونی آینه عبور نمی‌کنند، دلیل ایجاد انحراف کروی است. این پدیده، باعث تار شدن تصویر می‌شود. برای کم کردن انحراف کروی، شعاع انحنای آینه کروی باید بزرگ باشد. این کار باعث می‌شود که اختلاف فاصله پرتوها و محور اصلی، محدود شود.

همچنین برای از بین بردن اثر انحراف کروی، از «آینه سهموی» (Parabolic Mirror) استفاده می‌شود. تلسکوپ هابل شامل یک آینه سهموی بود، اما نقص در ساخت این آینه، یک ماموریت ویژه برای تجهیز مجدد تلسکوپ را ضروری کرد. از آینه‌های سهموی در ساخت تلسکوپ‌های با کیفیت و قطعات متمرکز کننده امواج الکترومغناطیسی مثل آنتن‌ها، استفاده‌های فراوانی می‌شود.

از رفلکتورهای سهموی برای تولید پرتوهای متمرکز موازی در چراغ قوه، لامپ و نور ماشین استفاده می‌شود. اگر یک منبع نوری در نقطه کانونی آینه قرار گیرد، نور به موازات محور اصلی آینه بازتاب می‌کند. به این ترتیب، یک پرتو باریک موازی ایجاد می‌شود.

همانطور که گفتیم، در آینه‌های مقعر دو نقطه به نام‌های مرکز انحنا (C) و نقطه کانونی (F) مهم هستند. فاصله بین مرکز تقارن آینه و مرکز انحنا،  شعاع انحنای آینه نام دارد. فاصله کانونی نیز فاصله بین نقطه کانونی و مرکز تقارن آینه است. به آینه‌های مقعر،‌ آینه‌های همگرا کننده نیز می‌گویند. زیرا نور در این آینه‌ها در نقطه کانونی جلوی آینه جمع می‌شود.

تصویر شیء‌ در آینه‌های مقعر

تصویر یک شیء‌ در آینه می‌تواند حقیقی یا مجازی و مستقیم یا معکوس باشد. اندازه تصویر نسبت به شیء نیز می‌تواند کوچکتر یا بزرگتر باشد. در ادامه به بررسی خصوصیات تصویر تشکیل شده از شیء‌ در آینه مقعر خواهیم پرداخت.

روش ترسیم اشعه و مکان‌یابی تصویر شیء در آینه مقعر

یک روش برای به دست آوردن تصویر شیء در آینه‌های کروی، «روش ردیابی یا ترسیم اشعه» (Ray Tracing Method) است.

در این روش، از شیء به آینه پرتو تابانده می‌شود. سپس از قوانین انعکاس استفاده می‌شود و پرتوهای بازتابی از آینه ترسیم می‌شوند. اگر این پرتوها به هم برسند، یک تصویر تشکیل می‌شود. با ترکیب این روش و هندسه پایه، می‌توان نقطه کانونی، محل تصویر تشکیل شده از شیء در آینه و خصوصیات آن را پیش‌بینی کرد.

در شکل زیر، یک شی بین نقطه کانونی و مرکز انحنای آینه مشاهده می شود:

در روش ردیابی اشعه، یک سری پرتوهای مشخص از شیء به آینه تابانده می‌شود و از پرتوهای تصادفی استفاده نمی‌شود. پرتوهای مشخص در روش ردیابی اشعه به صورت زیر تعریف می‌شوند:

پرتو موازی، به موازات محور اصلی آینه است. در آینه‌های مقعر پرتو موازی، پس از برخورد به آینه، در نقطه کانونی همگرا می‌شود. به همین ترتیب، اگر یک پرتو از نقطه کانونی آینه مقعر بگذرد و به آن برخورد کند، به موازات محور اصلی آینه بازتاب می‌کند. در نهایت، اگر یک پرتو از مرکز انحنای آینه عبور کند،‌ پرتو بازتاب یافته همان مسیر پرتو برخوردی را طی می‌کند و از مرکز انحنای آینه در جهت معکوس می‌گذرد.

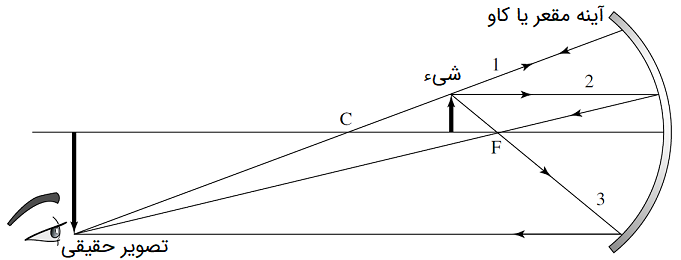
در شکل (۶)، سه پرتو مشخص ۱، ۲ و ۳ از شیء به آینه تابانده شده است. این شیء، بین نقطه کانونی و مرکز انحنای آینه قرار دارد. سه پرتو پس از برخورد به آینه، همگی در یک نقطه جمع می‌شوند. طبق روش ردیابی اشعه، تصویر شیء در آینه مقعر به صورت زیر تشکیل می‌شود:

• پرتو ۱ پس از ترک شیء به آینه برخورد می‌کند و از مرکز انحنای آینه می‌گذرد.
• پرتو ۲ به صورت افقی و به موازات محور اصلی شی را ترک می‌کند. این پرتو پس از برخورد به آینه، بازتاب می‌یابد و از نقطه کانونی آینه عبور می‌کند.
• پرتو ۳ پس از ترک شیء از نقطه کانونی آینه عبور می‌کند. پرتو بازتاب‌یافته به موازات محور افقی آینه است و از آن دور می‌شود.

نقطه برخورد سه اشعه، بازتاب نقطه متناظر آن در شیء است. محل تشکیل تصویر در شکل (۶)، پشت مرکز انحنای آینه است. این تصویر،‌ بزرگتر از جسم و معکوس است. از آنجایی که تصویر در سمت شیء و جلوی آینه قرار دارد، به آن تصویر واقعی گفته می‌شود. یک تصویر واقعی را می‌توان روی پرده انداخت. مفاهیم مطرح شده، اساس روش ردیابی پرتو است.

حال این سوال مطرح می‌شود که با معکوس شدن موقعیت چه اتفاقی رخ می‌دهد. در این حالت، جسم پشت مرکز انحنای آینه قرار دارد. شکل زیر این مسئله را نشان می‌دهد:

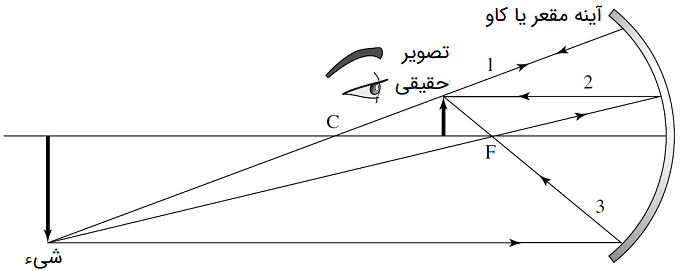
می‌توان با استفاده از همان سه پرتو مشخص و مانند شکل (۶)، تصویر شیء را تشکیل داد. در این حالت، تصویر بین مرکز انحنا و نقطه کانونی آینه قرار می‌گیرد. این تصویر، نسبت به شیء معکوس و کوچکتر است. همچنین در این حالت تصویر ایجاد شده از شیء در آینه مقعر حقیقی است، زیرا در سمت شیء تشکیل می‌شود. پس می‌توان تصویر را روی پرده انداخت تا قابل مشاهده شود.

ممکن است محل قرارگیری شی به آینه نزدیکتر باشد. مثلا اگر شی، بین نقطه کانونی و آینه باشد، می‌توان از روش ردیابی اشعه استفاده کرد. شکل زیر این مسئله را نشان می‌دهد:

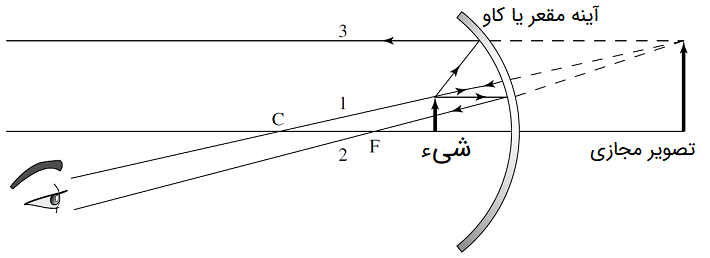
در این حالت، بازتاب سه پرتو جلوی آینه نخواهد بود و این سه پرتو، در پشت آینه به یکدیگر می‌رسند. همانطور که در شکل نیز مشخص است، در این حالت تصویر، غیر حقیقی و مجازی است. پرتوها پس از برخورد به آینه از یکدیگر دور می‌شوند. اما ناظر فکر می‌کند که تصویری مجازی از پشت آینه به چشم او می‌رسد.

معادله آینه

در مبحث آینه تخت مشاهده کردیم که تصویر شی در آینه تخت، مستقیم است و اندازه‌ای برابر دارد و پشت آینه تشکیل می‌شود. فاصله تصویر در آینه تخت تا آینه، با فاصله شیء تا آینه برابر است.

می‌توان با استفاده از مفاهیم پایه هندسه مانند آنچه در آینه تخت مشاهده شد، به روابطی ساده برای فواصل شیء و تصویر تا نقطه کانونی در آینه‌های کروی رسید.

شکل زیر را در نظر بگیرید:

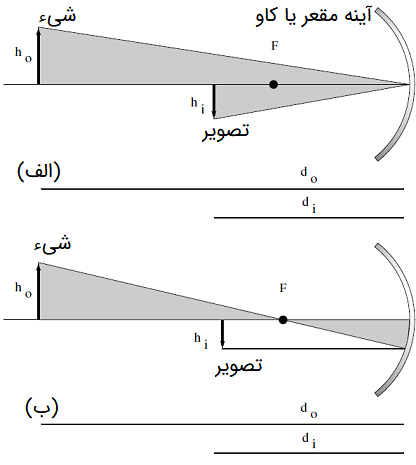
می‌توان محل تشکیل تصویر را محاسبه کرد. مطابق شکل (۹)، دو پرتو از شیء به آینه تابانده می‌شود. بازسازی تصویر با استفاده از روش ردیابی پرتو، انجام می‌شود.

در این شکل:

• $$h_o$$ ارتفاع شی است.
• $$h_i$$ ارتفاع تصویر است.
• $$d_o$$ فاصله شی از مرکز تقارن آینه است.
• $$d_i$$ فاصله تصویر از مرکز تقارن آینه است.

مثلث‌ها در شکل (۹)، تشابه دارند. بنابراین می‌توان یک تناسب بین فاصله‌ها و ارتفاع‌ها برقرار کرد. زوایا در این مثلث‌ها برابر است، پس اندازه اضلاع با هم برابر است. بنابراین داریم:

شکل (الف)، کاربرد «قانون اسنل» (Snell's Law) را نشان می‌دهد. طبق این قانون زاویه برخورد با زاویه بازتاب با یکدیگر برابر هستند. بنابراین با توجه به تشابه مثلث‌ها داریم:

$$\frac{h_o}{h_i}=\frac{d_o}{d_i}$$
معادله (۷)

در شکل (ب) و با توجه به تشابه مثلث‌ها، می‌توان رابطه زیر را نوشت:

$$\frac{h_o}{h_i}=\frac{(d_o - f)}{f}$$
معادله (۸)

با برابر قرار دادن این روابط (۷) و (۸) خواهیم داشت:

$$\frac{d_o}{d_i}=\frac{(d_o - f)}{f}$$
معادله (۹)

یا به عبارت دیگر:

$$\frac{1}{d_o}+\frac{1}{d_i}=\frac{1}{f}$$
معادله (10)

رابطه (۱۰) به نام «معادله آینه» (The Mirror Equation) مشهور است. این معادله، یک رابطه بین فاصله شی از آینه و فاصله تصویر از آینه و نقطه کانونی آینه برقرار می‌کند. معادله آینه تا زمانی که تقریب زاویه کوچک قابل اعمال باشد، معتبر است.

معادله آینه را می‌توان برای آینه‌های تخت نیز تعمیم داد. شعاع انحنای آینه تخت برابر بی‌نهایت است. بنابراین، نقطه کانونی آینه تخت در بی‌نهایت است. با توجه به رابطه (۱۰)، معادله آینه به صورت زیر نوشته می‌شود:

$$d_o = -d_i$$

در معادله آینه، توجه به علامت‌های فاصله‌ها بسیار ضروری است. مثلا برای آینه تخت، فاصله تصویر از آینه علامتی مخالف با فاصله شیء از آینه دارد.

مطابق شکل (۹) هنگامی که شیء بین کانون و مرکز انحنای آینه یا پشت مرکز انحنای آینه باشد، تصویری به وجود آمده در آینه مقعر معکوس شیء است. به همین دلیل، ارتفاع تصویر ($$h_i$$) باید علامتی مخالف با ارتفاع شیء ($$h_o$$) داشته باشد.

پس در معادله آینه باید به نکات زیر توجه کرد:

1. در آینه‌های مقعر، فاصله کانونی یک عدد مثبت در نظر گرفته می‌شود.
2. فاصله تصویر از آینه ($$d_i$$) برای تصاویر حقیقی مثبت و برای تصاویر مجازی، منفی است.

بزرگنمایی آینه مقعر

به عنوان یک مثال فرض کنید که یک تصویر مستقیم و بزرگتر از شیء در آینه مقعر مطلوب باشد.

شکل (۸)، خواص مطلوب مسئله را دارد. اگر یک شیء داخل فاصله کانونی آینه قرار داده شود، تصویر به دست آمده مستقیم و مجازی و بزرگتر خواهد بود. پس اگر ناظر در فاصله ۱۲ سانتی‌متری آینه قرار گیرد، فاصله کانونی برای این آینه مقعر باید مثلا ۲۰ سانتی‌متر باشد. بنابراین شعاع انحنای این آینه، ۴۰ سانتی‌متر است. حال برای یافتن تصویر این شیء در آینه از معادله آینه استفاده می‌کنیم.

می‌دانیم:

$$\frac{1}{d_o}+\frac{1}{d_i}=\frac{1}{f}$$

با قرار دادن اعداد در این معادله داریم:

$$\frac{1}{12.0}+\frac{1}{d_i}=\frac{1}{20.0}$$

در این حالت $$d_i=-30.0$$ است. همانطور که بیان شد، اگر فاصله تصویر از آینه منفی باشد، نشان می‌دهد که تصویر در پشت آینه تشکیل می‌شود و مجازی است.

«بزرگ نمایی آینه» (Image Magnification) به صورت نسبت ارتفاع تصویر به ارتفاع شی، ($$\frac{h_o}{h_i}$$) تعریف می‌شود. طبق تشابه مثلث‌ها می‌توان گفت:

$$\frac{h_o}{h_i}=\frac{d_o}{d_i}$$

بنابراین:

بزرگنمایی آینه= $$-\frac{d_i}{d_o}$$

علامت منفی به کار رفته در معادله بالا، به این معنی است که اگر تصویر مستقیم باشد، بزرگنمایی همواره یک عدد مثبت و اگر تصویر معکوس باشد، بزرگنمایی آینه عددی منفی است. همانطور که دیدیم، با قرار دادن شیء در فاصله ۱۲ سانتی‌متری جلوی آینه، تصویر در فاصله منفی سی سانتی‌متری پشت آینه قرار گرفت. پس می‌توان گفت بزرگنمایی آینه برابر است با:

$$m=\frac{30}{12}=2.5$$

اگر فاصله شیء از آینه ۱۲ سانتی‌متر باشد، بزرگنمایی این آينه مقعر برابر ۲.۵ است.

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس فیزیک
• آموزش جامع فیزیک دبیرستان
• مجموعه آموزش‌های ریاضیات و فیزیک پایه
• آموزش فیزیک پایه 1
• آموزش فیزیک پایه 2
• دوگانگی موج و ذره — به زبان ساده