کاردزدی (Work Stealing) در جاوا – از صفر تا صد
در این مقاله به بررسی مفهوم کاردزدی در جاوا خواهیم پرداخت. منظور از کاردزدی (Work Stealing) نوعی راهبرد زمانبندی برای برنامههای رایانهای چندنخی در محاسبات موازی است. به این ترتیب مشکل اجرای محاسبات چندنخی به روش دینامیکی حل میشود. در این روش محاسبات، فرد میتواند نخهای اجرایی جدیدی را روی یک رایانه چندنخی به روش استاتیک با تعداد ثابتی پردازنده یا هسته ایجاد کند. این راهبرد از نظر زمان اجرا، مصرف حافظه و ارتباط بین پردازندهای عملکرد بسیار بهینهای دارد.
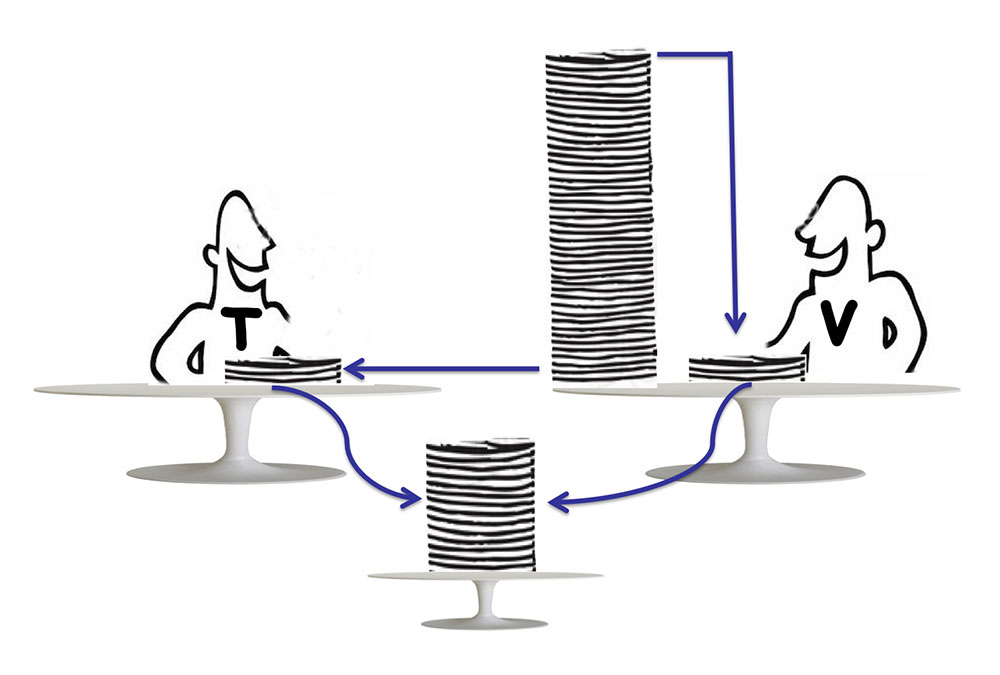

کار دزدی در جاوا
مفهوم کاردزدی با هدف کاهش تنازع در اپلیکیشنهای چندنخی در جاوا معرفی شده است. این کار با استفاده از فریمورک fork/join انجام مییابد.
رویکرد حل و تقسیم
در فریمورک fork/join، مسائل یا وظایف به طور بازگشتی به وظایف فرعی تجزیه میشوند. این در ادامه وظایف فرعی به صورت منفرد حل شده و نتایج هر یک با هم ترکیب میشوند تا نتیجه نهایی را تشکیل دهند:
نخهای کارگر
وظیفهای که تجزیه شده است به کمک «نخهای کارگر» (worker threads) حل میشود که از سوی «استخر نخ» (thread pool) تأمین میشوند. هر نخ کارگر دارای برخی وظایف فرعی است که مسئولیتشان را بر عهده گرفته است. این موارد در «صفهای دوطرفه» (deques) ذخیره میشوند.
هر نخ کارگر برخی وظایف فرعی را از deque خود میگیرد و به این ترتیب به طور پیوسته یک وظیفه فرعی را از ابتدای deque برمیدارد. زمانی که deque یک نخ کارگر خالی باشد، به این معنی است که همه وظایف فرعی برداشته شده و کار پایان یافته است.
در این زمان، نخ کارگر به صورت تصادفی یک نخ همتا را از استخر نخ انتخاب میکند تا بتواند کار آن را سرقت کند. سپس از رویکرد «ورودی اول-خروجی اول» (LIFO) برای برداشتن وظایف فرعی از انتهای deque قربانی استفاده میکند.
پیادهسازی فریمورک Fork/Join
ما میتوانیم یک استخر نخ کاردزدی با استفاده از یکی از کلاسهای ForkJoinPool (+) یا Executors (+) بسازیم:
کلاس Executors یک متد OVERLOAD-شده به نام newWorkStealingPool دارد که یک آرگومان عدد صحیح میگیرد که نماینده سطح «موازیسازی» (parallelism) است.
همچنین Executors.newWorkStealingPool یک تجرید از ForkJoinPool.commonPool است. تنها تفاوت در این است که Executors.newWorkStealingPool یک استخر در حالت ناهمگام میسازد که ForkJoinPool.commonPool این کار را انجام نمیدهد.
استخرهای نخ همگام و ناهمگام
ForkJoinPool.commonPool از یک پیکربندی صف به روش «ورودی آخر-خروجی اول» (LIFO) بهره میگیرد، در حالی که Executors.newWorkStealingPool از رویکرد «ورودی اول-خروجی اول» (FIFO) استفاده میکند.
بر اساس گزارش Doug Lea، رویکرد FIFO مزیتهای زیر را نسبت به رویکرد LIFO دارد:
- میزان تنازع را از طریق الزام سارقان به عملکرد روی سمت مقابل صف کاهش میدهد.
- از مشخصه حل و تقسیم الگوریتمهای بازگشتی برای تولید وظایف بزرگتر در زمانهای متقدم بهرهبرداری میکند.
نکته دوم به این معنی است که امکان تجزیه بیشتر یک وظیفه سرقت شده قدیمی از سوی نخی که آن را دزدیده است، وجود دارد.
بر اساس مستندات جاوا تعیین مقدار true برای asyncMode میتواند برای استفاده روی وظایف به سبک رویداد که هرگز join نمیشوند مناسب باشد.
مثال عملی: یافتن اعداد اول
در این بخش از مثال یافتن اعداد اول در میان مجموعهای از اعداد برای نمایش مزیتهای فریمورک کاردزدی از نظر زمان محاسباتی استفاده میکنیم. همچنین تفاوتهای بین استفاده از استخرهای نخ همگام و ناهمگام را نیز بررسی خواهیم کرد.
مسئله اعداد اول
یافتن اعداد اول از یک مجموعه از اعداد میتواند از نظر محاسباتی کار سنگینی باشد. یکی از دلایل عمده آن اندازه مجموعه اعدادی است که جستجو میکنیم. کلاس PrimeNumbers به یافتن اعداد اول کمک میکند:
چند نکته مهم وجود دارند که باید در مورد این کلاس متذکر شویم:
- این کلاس، RecursiveAction را بسط میدهد که به ما امکان میدهد تا متد compute مورد استفاده در وظایف محاسباتی را با استفاده از یک استخر نخ پیادهسازی کنیم.
- این کلاس به صورت بازگشتی وظایف را بر مبنای مقدار گرانولاریتی (granularity) به وظایف فرعی تجزیه میکند.
- سازندههای کلاس مقادیر کران پایین و بالایی را دریافت میکنند که بازه اعدادی را که میخواهیم اعداد اولش را مشخص کنیم تعیین میکند.
- این کلاس به ما امکان میدهد که اعداد اول را با استفاده از استخر نخ کاردزدی یا یک نخ منفرد تعیین کنیم.
حل سریعتر مسئله با استخرهای نخ
در این بخش اعداد اول را به روش نخ منفرد و همچنین استفاده از استخرهای نخ کاردزدی حل میکنیم. ابتدا رویکرد تکنخی را بررسی میکنیم:
و اینک از رویکرد ForkJoinPool.commonPool استفاده میکنیم:
در نهایت به بررسی رویکرد بهرهگیری از Executors.newWorkStealingPool میپردازیم:
ما از متد invoke کلاس ForkJoinPool برای ارسال وظایف به استخر نخ بهره گرفتهایم. این متد وهلههای کلاسهای فرعی RecursiveAction را میگیرد. سپس با استفاده از Microbench Harness (+) این رویکردهای مختلف را از نظر زمان میانگین هر عملیات با هم مقایسه میکنیم:
روشن است که هر دو رویکرد ForkJoinPool.commonPool و Executors.newWorkStealingPool امکان تعیین اعداد اول را به روشی سریعتر از رویکرد تکنخی به ما میدهند.
فریمورک استخر fork/join امکان تجزیه وظیفه را به وظایف فرعی فراهم میسازد. به این ترتیب مجموعه 10،000 عدد صحیح را به دستههای 1 تا 100، 101 تا 200، 201 تا 300 و همین طور تا آخر تجزیه میکنیم. سپس اعداد اول هر دسته را مشخص ساخته و تعداد کل اعداد اول را با استفاده از متد noOfPrimeNumbers به دست میآوریم.
کاردزدی برای محاسبه
در زمان بهرهگیری از یک استخر نخ ناهمگام، ForkJoinPool.commonPool نخ را تا زمانی که وظیفه در حال پردازش است در یک استخر قرار میدهد. در نتیجه سطح کاردزدی به سطح گرانولاریتی وظیفه ربطی ندارد.
از سوی دیگر Executors.newWorkStealingPool به صورت ناهمگام مدیریت بیشتری دارد و امکان وابستگی سطح کاردزدی به سطح گرانولاریتی وظیفه را فراهم ساخته است.
ما سطح کاردزدی را با استفاده از getStealCount در کلاس ForkJoinPool به دست میآوریم:
تعیین تعداد کاردزدی برای Executors.newWorkStealingPool و ForkJoinPool.commonPool رفتار نامشابهی را نشان میدهد:
زمانی که گرانولاریتی از کم به زیاد (از 1 به 10،000) تغییر مییابد، سطح کاردزدی در Executors.newWorkStealingPool کاهش مییابد. از این رو تعداد سرقت چیزها برابر با زمانی است که وظیفه تجزیه نشده است. اما ForkJoinPool.commonPool رفتار متفاوتی دارد. سطح کاردزدی همواره بالا است و چندان تحت تأثیر تغییر در گرانولاریتی وظیفه قرار ندارد.
به بیان فنی، مثال اعداد اول ما از پردازش ناهمگام وظایف به سبک رویداد پشتیبانی میکند. دلیل این امر آن است که پیادهسازی ما الزامی به الحاق نتایج ندارد. البته میتوان حالتی را تصور کرد که Executors.newWorkStealingPool بهترین امکان بهرهبرداری از منابع را برای حل مسئله ارائه میکند.
سخن پایانی
ما در این مقاله به بررسی کاردزدی در جاوا و شیوه استفاده از آن با استفاده از فریمورک fork/join پرداختیم. همچنین مثالهای عملی کاردزدی و شیوه بهرهگیری از آن برای بهبود پردازش از نظر زمان و منابع را بررسی کردیم.












