توزیع نرمال بریده شده (Truncated Normal Distribution) – به زبان ساده

در نظریه آمار و احتمال، توزیع‌های آماری نقش مهمی در توصیف پدیده‌های تصادفی دارند. یکی از توزیع‌های آماری که از توزیع نرمال منشعب شده است، «توزیع نرمال بریده شده» (Truncated Normal Distribution) است. البته در ادامه خواهیم دید که توزیع نرمال بریده شده را می‌توان حالت کلی‌تری برای توزیع نرمال در نظر گرفت. فرض کنید متغیر تصادفی $$X$$ دارای توزیع احتمالی نرمال باشد، اگر مجموعه مقادیر این متغیر تصادفی را در بازه $$(a,b)$$ محدود کنیم، متغیر تصادفی حاصل دارای توزیع «نرمال بریده شده» خواهد شد. از این توزیع بخصوص در مباحث مربوط به اقتصاد و داده‌های مالی استفاده زیادی می‌شود.

از آنجایی که این توزیع رابطه مستقیمی با توزیع نرمال دارد، خواندن مطلب توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها توصیه می‌شود. همچنین خواندن مطلب امید ریاضی (Mathematical Expectation) — مفاهیم و کاربردها نیز خالی از لطف نیست.

توزیع نرمال بریده شده

در توزیع نرمال بریده شده، تکیه‌گاه متغیر تصادفی $$X$$ بازه $$(a,b)$$ است. بنابراین اگر $$X$$ دارای توزیع نرمال با میانگین $$\mu$$ و واریانس $$\sigma^2$$ باشد، آنگاه $$X$$ با توجه به قید $$-\infty \leq a$$ دارای توزیع نرمال بریده شده است.

فیلم آموزش نظریه صف Queueing theory در فرادرس

کلیک کنید

البته ممکن است یکی از کران‌های بازه $$(a,b)$$ بی‌نهایت باشد در این حالت، توزیع نرمال بریده شده یکطرفه (One tail) خواهد بود. اگر $$a$$ بی‌نهایت منفی باشد (کران پایین وجود نداشته باشد) آنگاه توزیع را بریده شده از راست (Right Truncated) می‌نامند. همچنین اگر کران بالا برای متغیر تصادفی $$X$$ وجود نداشته باشد ولی $$a$$ باشد، توزیع را بریده شده از چپ (Left Truncated) می‌نامند.

تابع توزیع احتمال و چگالی نرمال بریده شده

با توجه به تعریف متغیر تصادفی نرمال بریده شده، می‌توان تابع چگالی احتمال را برای $$a\leq x\leq b$$ به صورت زیر نوشت:

$$\large f(x;\mu ,\sigma ,a,b)={\frac {\phi ({\frac {x-\mu }{\sigma }})}{\sigma \left(\Phi ({\frac {b-\mu }{\sigma }})-\Phi ({\frac {a-\mu }{\sigma }})\right)}}$$

البته مشخص است که $$\mu$$ میانگین توزیع نرمال و $$\sigma$$ نیز انحراف استاندارد توزیع نرمال در نظر گرفته شده است. همچنین منظور از $$\phi(.)$$ نیز تابع چگالی نرمال استاندارد و $$\Phi(.)$$ هم تابع توزیع تجمعی نرمال استاندارد است.

همانطور که دیده می‌شود، توزیع نرمال بریده شده دارای چهار پارامتر است که به ترتیب میانگین ($$\mu$$) و انحراف استاندارد ($$\sigma$$) توزیع نرمال و همچنین کران پایین و کران بالای برای متغیر تصادفی $$X$$ است.

فرض کنید تبدیلات زیر را انجام داده‌ایم:

$$\large \xi ={\frac {x-\mu }{\sigma }}\\\large \alpha ={\frac {a-\mu }{\sigma }}\\ \large \beta ={\frac {b-\mu }{\sigma }} \\ \large Z=\Phi (\beta )-\Phi (\alpha )$$

آنگاه می‌توان تابع چگالی نرمال بریده شده را به صورت ساده‌تری که در ادامه قابل مشاهده است، نوشت.

$$\large f(x;\mu ,\sigma ,a,b)={\frac {\phi (\xi )}{\sigma Z}}$$

نکته: درصورتی که $$b=\infty$$ باشد، مقدار تابع توزیع تجمعی نرمال استاندارد در نقطه $$\dfrac{b-\mu}{\sigma}$$ برابر است با ۱. همچنین اگر $$a=-\infty$$ می‌توان نتیجه گرفت که $$\Phi \left({\tfrac {a-\mu }{\sigma }}\right)=0$$. به این ترتیب خواهیم داشت:

$$\large f(x;\mu ,\sigma , -\infty,\infty) =\dfrac{\phi(\frac{x-\mu}{\sigma})}{\sigma(1-0)}=\dfrac{\phi (\frac{x-\mu}{\sigma})}{\sigma}$$

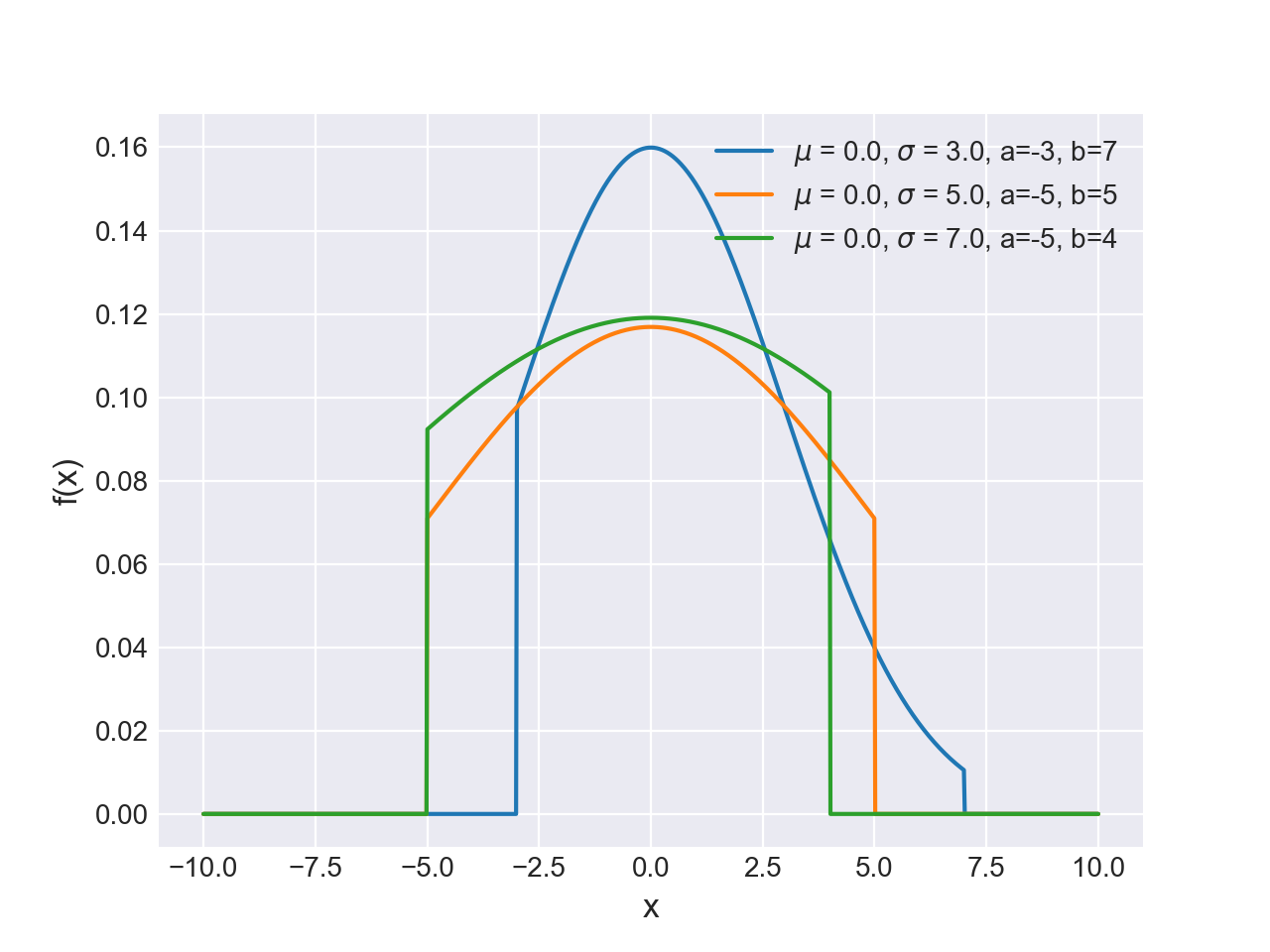
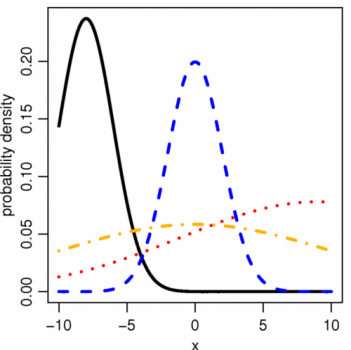
بدیهی است که عبارت بالا همان تابع چگالی نرمال است. پس می‌توان توزیع نرمال را حالت خاصی از توزیع نرمال بریده شده در نظر گرفت. منحنی تابع چگالی احتمال متغیر تصادفی نرمال بریده شده در تصویر زیر قابل مشاهده است. در این نمودار کران‌ها $$a=-10, \;b=10$$ در نظر گرفته شده‌اند. پارامترهای دیگر نیز برای خطوط سیاه رنگ به صورت $$\mu=-8,\; \sigma=2$$، برای خطوط آبی رنگ $$\mu=0,\; \sigma=2$$، برای خطوط قرمز رنگ $$\mu=9,\; \sigma=10$$ و برای خطوط زرد رنگ $$\mu=0,\; \sigma=10$$ منظور شده است.

همچنین در تصویر زیر منحنی چگالی نرمال بریده شده از چپ قابل مشاهده است.

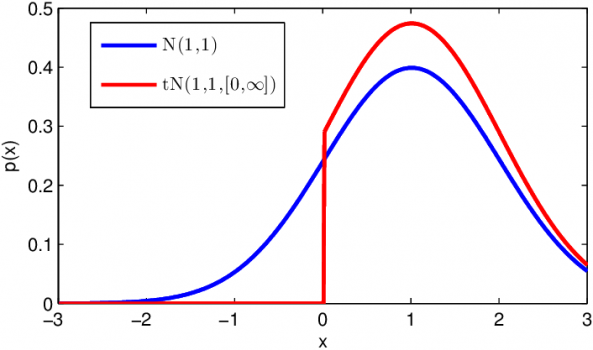
برای محاسبه تابع توزیع تجمعی متغیر تصادفی نرمال بریده شده، با توجه به تبدیلات گفته شده در بالا، می‌توان از رابطه زیر استفاده کرد.

$$\large F(x;\mu ,\sigma ,a,b)={\frac {\Phi (\xi )-\Phi (\alpha )}{Z}}$$

شکل تابع توزیع تجمعی نرمال بریده شده در تصویر زیر دیده می‌شود.

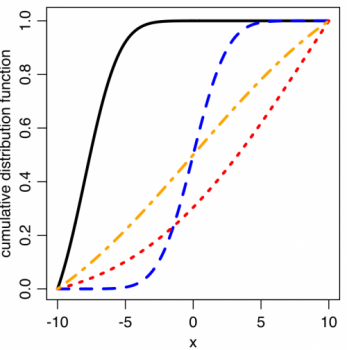
خصوصیات توزیع نرمال بریده شده

با توجه به ارتباطی که بین متغیر تصادفی نرمال و نرمال بریده شده وجود دارد، می‌توان امید ریاضی، واریانس و دیگر مشخصات توزیع نرمال بریده شده را براساس توزیع نرمال، بازنویسی کرد.

فیلم آموزش توزیع نرمال در آمار و کاربرد آن در علوم انسانی (رایگان) در فرادرس

کلیک کنید

امید ریاضی و واریانس توزیع نرمال بریده شده

از آنجایی که تابع چگالی احتمال متغیر تصادفی نرمال بریده شده با توجه به قیدی که برای مجموعه مقادیر $$X$$ وجود دارد، نوشته می‌شود، امید ریاضی این توزیع را می‌توان به صورت زیر نوشت.

$$\large \operatorname {E} (X\mid a$$

توجه داشته باشید که تعریف‌های مربوط به $$\alpha$$، $$\beta$$ و $$Z$$ به همان شکلی است که در بالا توضیح داده شد. به همین ترتیب، میانه (Median) و نما (Mode) برای این توزیع به صورت زیر محاسبه می‌شوند.

$$\large \operatorname{Median}(X) = \mu +\Phi ^{-1}\left({\frac {\Phi (\alpha )+\Phi (\beta )}{2}}\right)\sigma$$

$$\large \operatorname{Mode}(X)= \left\{{\begin{array}{ll}a,&\mathrm {if} \ \mu b\end{array}}\right.$$

برای محاسبه واریانس نیز از رابطه زیر می‌توان کمک گرفت.

$$\large \operatorname {Var}(X)= \sigma ^{2}\left[1+{\frac {\alpha \phi (\alpha )-\beta \phi (\beta )}{Z}}-\left({\frac {\phi (\alpha )-\phi (\beta )}{Z}}\right)^{2}\right]$$

نکته: اگر توزیع نرمال بریده شده به صورت یک طرفه (بریده شده از راست یا چپ) باشد، برای محاسبه امید ریاضی و واریانس به صورت زیر عمل می‌کنیم.

امید ریاضی و واریانس نرمال بریده شده از چپ:

$$\large \operatorname {E} (X\mid X>a)=\mu +\sigma \phi (\alpha )/Z \\ \large \operatorname {Var} (X\mid X>a)=\sigma ^{2}[1+\alpha \phi (\alpha )/Z-(\phi (\alpha )/Z)^{2}]$$C

با توجه به اینکه $$\Phi(+\infty)=1$$ است، در اینجا $$Z=1-\Phi(\alpha)$$ است.

امید ریاضی و واریانس نرمال بریده شده از راست:

$$\large \operatorname {E} (X\mid X$$

شبیه سازی داده‌های نرمال بریده شده

اگر مقدارهای متغیر تصادفی $$X$$، برطبق رابطه زیر محاسبه شوند، می‌توان آن را یک متغیر تصادفی نرمال بریده شده در بازه $$(a,b)$$‌ در نظر گرفت.

$$\large X=\Phi ^{-1}(\Phi (\alpha )+U\cdot (\Phi (\beta )-\Phi (\alpha )))\sigma +\mu$$

در این رابطه منظور از $$\Phi$$ تابع احتمال تجمعی توزیع نرمال استاندارد و $$\Phi^{-1}$$ نیز معکوس آن است. همچنین $$U$$ یک متغیر تصادفی یکنواخت پیوسته در بازه (0,1) است. بنابراین از این رابطه می‌توان برای تولید داده‌هایی با توزیع نرمال بریده شده استفاده کرد. به این شیوه تولید اعداد تصادفی «روش تبدیل معکوس» (Inverse Transform Method) می‌گویند که قادر است از هر توزیعی (به شرطی معکوس‌پذیر بودن تابع توزیع تجمعی آن) اعداد تصادفی تولید کند. برای تولید چنین داده‌هایی در نرم‌افزارهای محاسباتی R و matlab کافی است از تابع $$trandn$$ استفاده کنید.

اگر به فراگیری مباحث مشابه مطلب بالا علاقه‌مند هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش‌های SPSS
• مجموعه آموزش‌های نرم‌افزارهای آماری
• آموزش آمار و احتمال مهندسی
• توزیع های آماری — مجموعه مقالات جامع وبلاگ فرادرس

^^