تناقض سیمپسون (Simpson’s Paradox) – به زبان ساده
در این مطلب به «تناقض سیمپسون» (Simpson's Paradox) میپردازیم. این موضوع به ما یادآور میشود که عدم توجه به بعضی از جنبههای فرض مسئله، ممکن است دو جواب کاملا متناقض برای حل یک مشکل نصیبمان کند. گاهی به جای کلمه تناقض از عبارت پارادوکس نیز در چنین مواردی استفاده میشود. بنابراین میتوان گفت که در اینجا منظور از تناقض همان «پارادوکس سیمپسون» (Simpson's Paradox) است.


تصور کنید که شما و همسرتان، به دنبال یک رستوران خوب برای شام میگردید. بنابراین هر کدام از شما با استفاده از نظرسنجی شبکههای اجتماعی مناسبترین رستوران را برای شام امشب جستوجو میکنید. فرض کنید شما رستوران «طلایی» را پیدا کردهاید که درصد رضایت بیشتری در بین مردان و زنان را نسبت به رستورانی دارد که همسرتان پیدا کرده است. فرض کنید که نام رستوران منتخب همسر شما، رستوران «خوشمزه» است. هر چند رستوران طلایی درصد رضایت بیشتری را در بین زنان و مردان دارد نسبت به رستوانر خمشمزه دارد ولی همسر شما مدعی است که رستوران او، رضایت کلی بیشتری (بدون در نظر گرفتن جنسیت) نسبت به رستوران طلایی دارد. نکته جالب این است که هر دو براساس یک منبع اطلاعاتی به نتایج کاملا متفاوتی رسیدهاید. جالبتر آن است که به نظر میرسد که حق با هر دوی شماست و هر دو دلیل موجهی برای ادعای خود دارید.
مشکل ناشی از چه چیزی است؟ این تناقض نشان دهنده چیست؟ چه کسی به نتیجه صحیح رسیده است؟ آیا نتایج نظر سنجی اشتباه است یا در محاسبات مشکلی وجود دارد؟ از نظر منطقی، هر دوی شما نتیجه صحیحی گرفتهاید و بدون آنکه بدانید وارد دنیای تناقض سیمپسون شدهاید. مسئلههایی مثل انتخاب بهترین یا بدترین رستوران و انتخاب ورزش مناسب برای کاهش یا افزایش ریسک یک بیماری خاص از جمله مواردی هستند که در آنها براساس دادههای یکسان ممکن است، استنتاجهای افراد، کاملا با یکدیگر متناقض باشد. پس مراقب باشید که بحث بر سر این تناقض آماری باعث نشود که امشب از شام رستوران بگذرید.
تناقض سیمپسون (Simpson's Paradox)
این تناقض زمانی رخ میدهد که یک مجموعه داده به گروههایی تقسیم شده باشد که نتایج حاصل از آنها در جهت خلاف با حالتی است که دادهها تجمیع شدهاند. در مثال مربوط به رستوران که در بالا ذکر کردیم، به نظر میرسد که رستوان طلایی با درصد رضایت بیشتر در بین زنان و مردان باید میزان رضایت بیشتری هم در کل نسبت به رستوران خوشمزه داشته باشد. با استفاده از مثال زیر نشان میدهیم که ممکن است چنین چیزی همیشه درست نباشد.
جدول زیر میزان رضایت برای هر دو رستوران را به تفکیک زن و مرد نمایش میدهد. با ترکیب میزان رضایت زنان و مردان در سطر آخر مشخص میشود که رستوران خوشمزه دارای رضایت بیشتری نسبت به رستوران طلایی است.
| رستوران خوشمزه | رستوران طلایی | |
| مردان | 50/150=33.۳٪ | 180/360= 50٪ |
| زنان | 200/250=80٪ | 36/40=90٪ |
| کل | 250/400-62.5٪ | 216/400=54٪ |
همانطور که دیده میشود، با اینکه رستوران طلایی در بین زنان و مردان از درصد رضایت بیشتری برخوردار است ولی در حالتی که همه افراد را ،بدون تفکیک از لحاظ جنسیتشان، در نظر میگیریم، میزان رضایت از رستوران خوشمزه کمتر خواهد بود. چگونه چنین چیزی ممکن است؟ این تناقض از چه چیزی ناشی میشود؟
از آنجایی که برای محاسبه درصدها از حجم نمونه متفاوتی از پاسخ دهندگان استفاده شده است، تناقض سیمپسون ظاهر میشود. هر کسر، نسبت تعداد کاربرانی راضی را نسبت به کل کاربران را محاسبه کرده است. در رستوران طلایی، مردانی که نظرشان مورد بررسی قرار گرفته نسبت به زنان خیلی بیشتر هستند و در رستوران خوشمزه، این حالت برعکس اتفاق افتاده است. از آنجایی که تعداد زنانی که در نظرسنجی رستوران طلایی مورد پرسش قرار گرفتهاند کمتر از مردان است، رضایتشان سهم کمتری نسبت به مردان در محاسبه درصد کل دارد. در ننتیجه میانگین کل اندکی نسبت به میانگین درصد رضایت مردان افزایش یافته است.
در مقابل تعداد زنانی که در نظرسنجی رستوران خوشمزه شرکت کردهاند بیشتر از مردان است. در نتیجه سهم آنها در محاسبه درصد کل، بیشتر از مردان است. در اینجاست که پارادوکس سیمپسون رخ داده.
در چنین مواقعی بهتر است تصمیم بگیریم که با توجه به چه جمعیت یا نمونهای میخواهیم درصدها را محاسبه کنیم، به تفکیک جنسیت یا بر حسب کل افراد. به هر حال شاید لازم باشد که دادهها را به نحوی با یکدیگر ترکیب کنیم ولی باید به نحوه و شیوه جمعآوری آنها (که مدل علّی، Causal Model نامیده میشود) نیز توجه داشته باشیم. با این کار دیگر دچار پارادوکس سیمپسون نمیشویم. در اینجا این سوال مطرح میشود که رویکرد مناسب برای انتخاب رستوران چیست؟ اجازه دهید این سوال را بعد از اینکه با یک مثال دیگر آشنا شدیم، پاسخ دهیم.
همبستگی معکوس
به عنوان یک مثال شهودی دیگر از پارادوکس سیمپسون میتوان به زمانی اشاره کرد که جهت همبستگی دادهها با حالتی که آنها را طبقهبندی کردهایم متفاوت باشد. به یک مثال ساده در این زمینه میپردازیم.
فرض کنید که ساعتهای تمرین در هفته و احتمال پیشرفت یک بیماری برای دو گروه بیمار اندازهگیری شده است. گروه اول زیر ۵۰ سال هستند و گروه دوم بالای ۵۰ سال سن دارند. در تصویر زیر برای هر یک از این گروهها، نمودار نقطهای برای سنجش رابطه بین میزان تمرین ورزشی و احتمال پیشرفت بیماری ترسیم شده است.
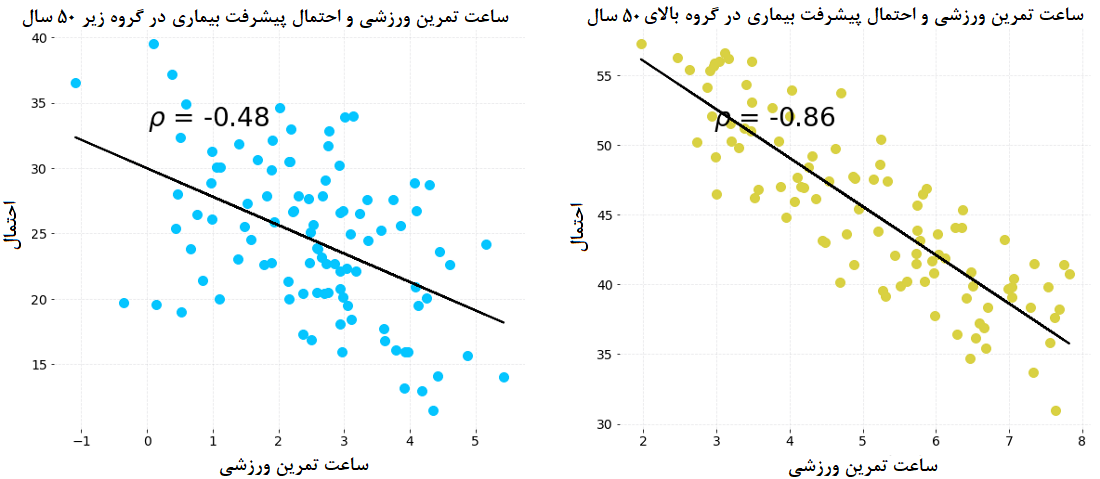
کاملا مشخص است که در هر دو گروه میزان فعالیت ورزشی در احتمال پیشرفت بیماری اثر عکس دارد. یعنی با افزایش ساعت ورزش، احتمال پیشرفت بیماری کاهش مییابد. حال این دادهها را ترکیب کرده و بر اساس اطلاعات ادغام شده در هر دو گروه، ضریب همبستگی بین میزان ساعات ورزش و احتمال پیشرفت بیماری را میسنجیم. در تصویر زیر، میزان همبستگی و نمودار رابطه بین دو متغیر را میتوان مشاهده کرد. حتما این نمودار را با نمودار بالایی مقایسه کنید.
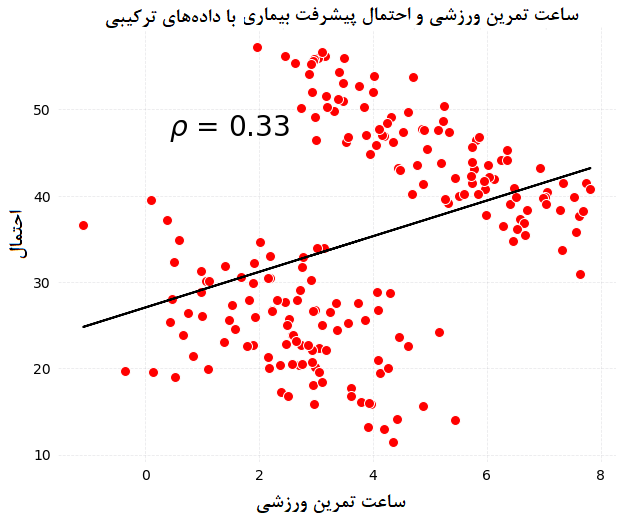
به طرز شگفتآوری، ضریب همبستگی مثبت شد. با توجه به این نمودار باید گفت که فعالیت ورزشی باعث افزایش ریسک ابتلا به بیماری میشود. پس بهتر است که ورزش نکنیم. این دقیقا متناقض با نتیجهای است که در قسمت قبلی حاصل شد. آیا فعالیت ورزشی میتواند هم تاثیر مثبت و هم منفی روی بیماری داشته باشد؟ برای پاسخ به این سوال باید به شکل و شیوهای که این اطلاعات جمعآوری شدهاند، بیشتر توجه کرد.
برطرف کردن تناقض سیمپسون
برای جلوگیری از پارادوکس سیمپسون، که منجر به نتایج متناقض میشود، باید تصمیم بگیریم که استنباط و نتایج را برحسب دادههای تفکیک شده لازم داریم و یا باید براساس تجمیع دادهها تصمیم مناسب را اتخاذ کنیم. این توضیح شاید واضح باشد ولی مشخص نمیکند که چه مواقعی به تفکیک و یا تجمیع احتیاج داریم. پاسخ این سوال در مفهوم تفکر علّی (Think Causally) نهفته است. به این معنی که منشا و پایه اطلاعات تولیدی را بشناسیم و متوجه باشیم که چه عامل یا عواملی، دادهها را تحت تاثیر قرار دادهاند که ممکن است از دید ماه پنهان مانده باشد.
در مثالی که در مورد بیماری و ورزش بیان شد، بطوری شهودی مشخص است که ساعات تمرین ورزشی تنها عامل موثر در بهبود یا پیشرفت بیماری نیست. عوامل دیگر مانند رژیم غذایی، محیط زندگی و وراثت نیز در بروز و پیشرفت بیماری موثر هستند. در حالیکه در نمودار ترسیم شده، فقط احتمال ابتلا به بیماری به همراه ساعات تمرین ورزشی نمایش داده شده است.
در مثال تخیلی ما، فرض کنید که احتمال ابتلا به بیماری به دو متغیر به نامهای زمان ورزش و سن مرتبط باشد. نمودار ارتباطی بین این عوامل در زیر دیده میشود. در این میان، دادههای جمعآوری شده، بیانگر دو نوع عامل برای پیشرفت بیماری هستند. با در نظر گرفتن ارتباط بین احتمال ابتلا به بیماری و ساعات ورزشی، در واقع، عامل سن نادیده گرفته شده است.
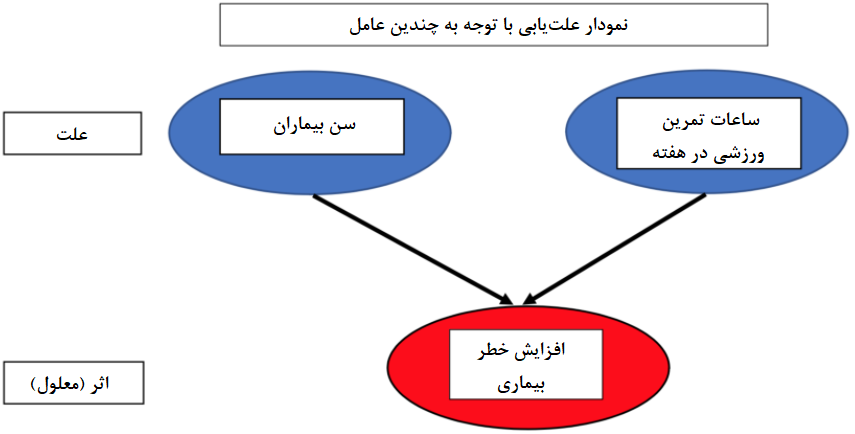
با توجه به این نکته، اگر برای هر دو گروه بالا 50 و کمتر از ۵۰ سال، مقدار ضریب همبستگی بین احتمال ابتلا به بیماری و سن را محاسبه و نمودار نقطهای بین این مقدارها را ترسیم کنیم، متوجه خواهیم شد که بین سن و احتمال ابتلا به بیماری، همبستگی شدیدی وجود دارد. به این معنی که با افزایش سن، احتمال ابتلا به بیماری نیز افزایش خواهد یافت. به این ترتیب مشخص است که احتمال بیمار شدن برای افراد مسن بیشتر از افراد جوانی است که به میزان برابر ورزش میکنند. برای اندازهگیری میزان اثر فقط ورزش بر روی بیماری، باید سن را ثابت در نظر گرفته و ساعات تمرین ورزشی را به عنوان متغیر در محاسبات منظور کنیم.
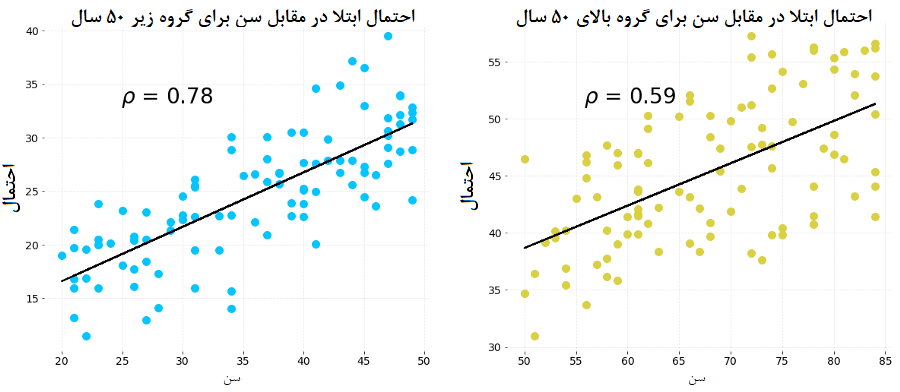
تفکیک دادههای به گروههای مجزا در چنین حالتی میتواند یک روش برای ثابت کردن یک متغیر در مقابل تغییر پذیری متغیر دیگر باشد. با این کار، در مثال ما، مشخص میشود که برای هر گروه سنی (بالا یا پایین ۵۰ سال)، ساعات تمرین ورزشی احتمال ابتلا به بیماری را کاهش میدهد. این همان چیزی است که در نمودارهای اولیه دیده شد. در آنجا با تفکیک دادهها به دو گروه، عامل سن بیماران کنترل و همبستگی بین میزان ساعات ورزشی و احتمال ابتلا به بیماری محاسبه شد.
با تشخیص نحوه جمعآوری دادهها و به کارگیری مدل علّی، پارادوکس سیمپسون قابل حل است. به این ترتیب طبقهبندی دادهها براساس عواملی که باید تحت کنترل قرار بگیرند چاره کار خواهد بود.
نحوه برخورد ما با پرسشها و مسائل، میتواند راهگشای حل آنها باشد. در مثال رستوران، میخواهیم تشخیص دهیم که کدام رستوان هم از نظر مردان و زنان مورد پسند است. از آنجایی که دسترسی به عوامل دیگری که در سنجش رضایت مشتریان رستوران دخیل است برایمان میسر نیست، مجبور به نادیده گرفتن آنها هستیم در حالیکه برای گریز از تناقض سیمپسون احتیاج به دادههای بیشتری داریم.
در نتیجه از تنقاض یا پارادوکس سیمپسون میتوان آموخت که استفاده از دادهها به تنهایی کافی نیست و شاید نیاز به کل داستان باشد تا بتوان به تصمیم درست رسید. به بیان دیگر، باید تصویر کامل و کافی از اطلاعات، نظیر نحوه جمعآوری آنها و عوامل موثر بر متغیر پاسخ و همچنین متغیرهایی که بر یکدیگر تاثیر گذارند در دسترس باشد تا هنگام تصمیمگیری چیزی از قلم نیفتاده باشد و در نهایت نتایج حاصل شده از استنباط برمبنای دادهها، دچار تناقض نشود.
اثر پارادوکس سیمپسون در زندگی روزانه
شاید به نظر برسد که این تناقض فقط در مسائل آماری به چشم میخورد. ولی میتوان با مثالهای متعددی، وجود این تناقض را در دنیای واقعی و زندگی روزمره متوجه شد. یک مثال میتواند اثر دو نوع درمان برای سنگ کلیه باشد. فرض کنید روش درمانی A و B دو شیوه برای درمان سنگ کلیه باشند. به نظر میرسد که روش A در درمان سنگهای کوچک و بزرگ بهتر از روش B است. اما با استنباط بر اساس دادههای تجمیع شده (بدون در نظر گرفتن اندازه سنگ) به نظر میرسد که روش درمانی B بهتر از A است. جدول زیر به درصد موفقیت این درمانها پرداخته است.
| درمان / اندازه سنگ | روش درمانی A | روش درمانی B |
| سنگ کوچک | 93٪ = (81/87) | 87٪= (234/27۰) |
| سنگ بزرگ | 73٪=(192/263) | 69٪= (55/80) |
| تجمیعی | 78٪= (273/350) | 83٪= (289/350) |
همانطور که دیده میشود، روش درمانی A در درمان سنگهای کوچک موفقتر از روش B است در حالیکه درصد موفقیت روش درمانی B در کل بیشتر از روش A است. چگونه چنین چیزی ممکن است؟
به نظر میرسد که باید به فرآیند تهیه اطلاعات و دادهها توجه بیشتری کنیم. هر چند که روش درمانی A بهتر از روش B در درمان سنگهای کوچک به نظر میرسد ولی وجود سنگهای کوچک در کلیه خیلی مساله حادی محسوب نمیشود. به همین علت پزشکان بیشتر ترجیح میدهند که روش درمانی B را که کمتر تهاجمی است (حتی با نرخ موفقیت کمتر) به کار گیرند زیرا مساله بیمار، خیلی وخیم نیست.
ولی همین پزشکان، برای درمان سنگهای کلیه بزرگ که مشکل جدی برای بیمار ایجاد میکند، از روش درمانی A که تهاجمیتر و البته موثرتر است استفاده میکنند. بنابراین اگر به نظر میرسد که روش درمانی A دارای درصد موفقیت کمتری نسبت به روش B است، علت وخیم بودن وضعیت بیمارانی است که از روش A برای درمانشان استفاده شده است در نتیجه تنها روش درمان بر موفقیت روش درمانی موثر نیست بلکه وضعیت وخامت بیماری نیز بر روی موفقیت تاثیر گذار است.
پس از نظر پزشکی روش A نسبت به روش B باید روش بهتر و موثرتری باشد ولی با توجه به تعداد درمانیهای بیشتری که توسط روش B صورت گرفته، بخصوص روی بیمارهایی که دارای سنگ کلیه کوچک هستند، به نظر میرسد که روش B در کل دارای درصد موفقیت بیشتری است.
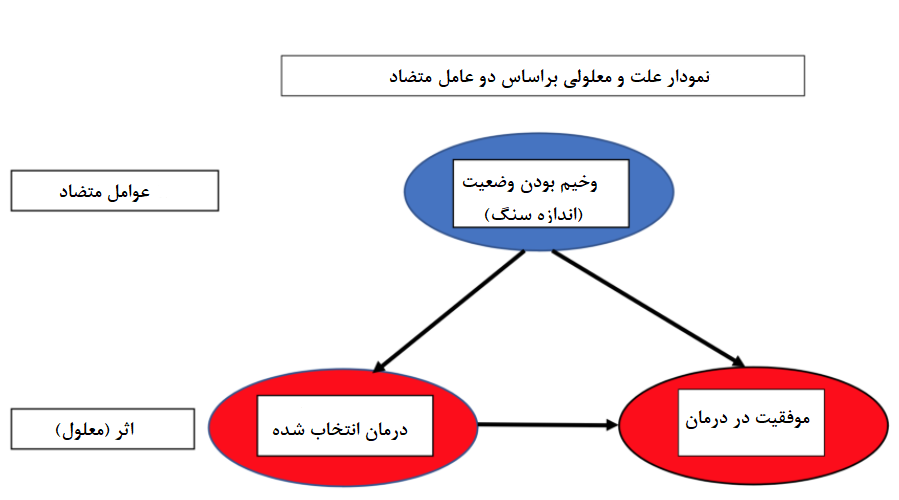
اثر یا معلول در این پرسش درمان بیماری است که به دو عامل روش درمان و اندازه سنگ (وخیم بودن بیماری) بستگی دارد. از طرف دیگر انتخاب شیوه درمان به اندازه سنگ بستگی داشته که باعث میشود، متغیر اندازه سنگ به صورت متغیر مداخلهگر (Confounding Variable) نقش داشته باشد.
برای آنکه تشخیص دهیم واقعا کدام روش درمانی مناسب است، باید متغیر مداخلهگر را به وسیله تفکیک به جای تجمیع کنترل کنیم. به این ترتیب براساس تفکیک دادهها متوجه میشویم که روش درمانی A، نسبت به روش درمانی B، روی بیمار موثرتر است. زیرا در هر دو گروه بیماران (سنگهای کوچک و بزرگ) دارای درصد موفقیت بزرگتری است.
بنابراین اگر شما دچار سنگ کلیه هستید، براساس جدول بالا، چه سنگ بزرگ داشته باشید یا کوچک، روش درمانی A را انتخاب خواهید کرد، زیرا درصد موفقیت بیشتری دارد و به این ترتیب پارادوکس حل میشود.
«گاهی به کارگیری دادههای تجمیع شده موثر و مفید است ولی در بعضی از مواقع نیز باعث سردرگمی و مخفی کردن واقعیت خواهد شد.»
اثبات یک نظریه و عکس آن
به عنوان یک مثال دیگر در دنیای واقعی از پارادوکس سیمپسون، میتوان به مسائل حوزه سیاستهای دولتها و وضعیت اقتصادی کشور توجه کرد.
در جدول زیر درآمد، مالیات و درصد مالیات برای گروههای درآمدی مختلف، به تفکیک دو دوره ریاست وزیر اقتصاد و دارایی (دوره A و B) ثبت شده است.

همانطور که دیده میرسد، براساس ستون مالیات و یا درصد مالیات به نظر میرسد که در دوره B نسبت به دوره A مالیات کاهش یافته است ولی در سطر آخر دیده میشود که درصد مالیات کل افزایش داشته است. برای حل این تناقض میدانیم که باید عوامل موثر بر مالیات را جستوجو کنیم. به نظر میرسد که درصد یا نرخ مالیات تابعی از دو عامل درصد مالیات در هر گروه مشمول مالیات و درآمد مشمول مالیات است. با توجه به تورم (یا افزایش حقوق و دستمزد) در دوره B، درآمد بیشتری در گروههای مشمول مالیات قرار گرفتهاند و درآمدهای مشمول مالیات در گروههای درآمدی پایینتر کمتر شده. به این ترتیب نرخ مالیات در دوره B به نظر بزرگتر میرسد.
برای مثال در دوره A، مجموع درآمد مشمول مالیات در رده درآمدی زیر ۵۰۰۰ برابر با حدود ۴۱ میلیون دلار است. در حالیکه در دوره B در این گروه، میزان درآمد مشمول مالیات تقریبا نصف دوره A است. ولی در دوره A گروهی که بین ۱۵ تا ۹۹ هزار دلار درآمد دارند، درآمد مشمول مالیاتشان حدود ۴۷۰ میلیون دلار است در حالیکه برای دوره B این مبلغ حدود دو برابر یعنی 865 میلیون دلار است. به این ترتیب میزان درآمدی که مشمول مالیات میشود در دوره B خیلی بیشتر از دوره A است و انتظار میرود که حاصل درآمد دولت از مالیات افزایش یابد. به این ترتیب مشخص میشود که در دوره B میزان دریافتی مالیات از اقشار کم درآمد کاهش داشته ولی برای افراد پر درآمد افزایش وجود دارد. در نتیجه درآمد دولت از مالیات افزایش داشته و در نتیجه نرخ مالیات در کل برای دوره B رشد نشان میدهد.
به هر حال باید دادهها را براساس پرسش و پاسخی که احتیاج داریم با یکدیگر ادغام کنیم. در این مثال دیده میشود که سیاستهای مختلف مالیاتی چگونه اعمال میشوند. اگر به عنوان یک فرد با درآمد متوسط به مسئله مالیات نگاه کنیم به نظر می رسد که باید نگران نرخ مالیات در گروه درآمدی خودمان باشیم که به نظر میرسد از دوره A به دوره B کاهش داشته است. البته به شرطی که از گروه درآمدی خود در طول دو دوره A و B خارج نشده باشیم. بنابراین نرخ مالیات در گروههای دیگر برای ما اهمیت نخواهد داشت.
چرا پارادوکس سیمپسون مهم است
تناقض سیمپسون بسیار اهمیت دارد زیرا به ما یادآوری میکند که دادهها آنطور که دیده میشوند نیستند. بنابراین به راحتی با نگاه کردن به یک نمودار یا جدول نمیتوان به یک استنباط یا تحلیل واقعی رسید، بلکه باید روند تولید اطلاعات و عوامل موثر بر نتایج را مورد بررسی و تحلیل قرار داد. به این ترتیب ممکن است شواهد به خوبی بر موضوعی دلالت کنند که منجر به گمراهی شود زیرا همه اطلاعات در اختیار ما در آن لحظه قرار ندارند. بهتر است به جای آنکه به داشتههای اطلاعاتی حال حاضر تکیه کنیم، به تحقیق پیرامون موضوع مورد بررسی بپردازیم و دادهها و اطلاعات جدید جمعآوری کنیم تا به کمک تفکر عمیق و علمی، به نتایج منطقیتر و موثرتری برسیم.
دادهها و اطلاعات، ابزار و سلاح قدرتمندی هستند، هم میتوانند به ما کمک کنند و هم ما را به گمراهی بکشند.
هنگامی که از کم و کیف تولید دادهها و چگونگی جمعآوری آنها مطلع شدیم به دنبال عوامل موثر میگردیم تا روابط علت و معلولی را کشف کنیم. این کار نه تنها یک روال پژوهش علمی محسوب میشود بلکه ما را از کسب نتایج انحرافی از دادهها و اطلاعات برحذر میدارد. به این منظور بهتر است از تجربیات افرادی که در زمینه مورد نظر تخصص دارند و بهتر میتوانند روابط علت و معلولی را تشخیص دهند کمک بگیریم. همانطور که دادهها و اطلاعات میتوانند به ما چراغی فروزان برای روشن کردن راه پر پیچ و خم تحلیل دادهها بدهند، ممکن است با غفلت از رفتار دادهها و روابط بین آنها به گمراهی کشیده شویم و تصمیمات نادرست را اتخاذ و اجرایی کنیم.
تناقض سیمپسون یک پدیده آماری جذاب است که نشان میدهد تفکر منطقی و منتقدانه میتواند سپری در برابر دغلکاری و گمراهکنندگی دادهها باشد.
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ریاضی و فیزیک
- آموزش مبانی منطق و نظریه مجموعه ها
- منطق ترکیبی به زبان ساده
- مجموعه آموزش های ریاضیات
- آموزش منطق مرتبه اول در هوش مصنوعی
- منطق دیجیتال و بررسی مبانی و مفاهیم
- ضریب همبستگی جزئی (Partial Correlation) — به زبان ساده
^^













سلام و تشکر برای مطلب مفید و آموزنده حتی برای من با زمینه متفاوت از آمار. یک سوال: چطور میشه مثالی برای این پارادوکس در صنعت رباتیک مثلا رباتهای مسیریاب عنوان کرد. فرض اینکه از نطقه شروع تا پایان ممکنه مسیرهای متعددی طی بشه با احتمالهای متفاوت. آیا مواردی که به پایان نمیرسندممکنه منجر به این پارادوکس بشه؟