انتقال از راه دور کوانتومی — Teleportation از ایده تا عمل

در این نوشته به توضیح امکان‌سنجی افسانه انتقال از راه دور کوانتومی می‌پردازیم و نمونه کدهایی ارائه می‌کنیم که با اجرای آن روی پلتفرم «تجربه کوانتوم آی‌بی‌ام» (IBM’s Quantum Experience) می‌توانید این امکان را در عمل مشاهده کنید. در این مقاله از QISKit استفاده شده و از این رو باید این SDK را دانلود و نصب کنید.

برای این که این مقاله را به درستی درک کنید، می‌بایست آشنایی مختصری با برهم‌نهی کوانتومی (Quantum superposition) و درهم‌تنیدگی کوانتومی (Quantum entanglement) داشته باشید.

همان طور که در ادامه خواهیم دید، انتقال راه دور کوانتومی (تله‌پورت کوانتومی) در واقع روی دیگر سکه کدگذاری فوق چگال (superdense coding) است. ما با استفاده از کدگذاری فوق چگال می‌توانیم دو بیت کلاسیک از اطلاعات را به وسیله تنها یک کیوبیت (qubit) منفرد ارسال کنیم. در انتقال راه دور کوانتومی، از دو بیت کلاسیک اطلاعات برای ارسال یک کیوبیت منفرد که وضعیت کوانتومی آن نامشخص است، استفاده می‌شود.

در این راهنما مباحث ریاضیات، مدارهای کوانتومی و کدهای مربوط به این پدیده را معرفی می‌کنیم. در این مسیر توضیح می‌دهیم که در هر گام چه رخ می‌دهد. پیش از آن که بحث را آغاز کنیم فرض ما این است که شما دانشی مقدماتی در مورد کیوبیت‌ها، نمادگذاری دیراکی (Dirac)، بیت‌های کلاسیک، و جبر خطی دارید. اگر به دنبال راهنمایی در مورد محاسبات کوانتومی هستید، پیشنهاد می‌کنیم مستندات IBM Q Experience را مطالعه نمایید.

فیلم آموزش جبر خطی در فرادرس

کلیک کنید

پیش از آن که وارد مفاهیم بنیادی شویم، نگاهی به قطعه کد پایتون می‌اندازیم که در مثال‌های خود استفاده خواهیم کرد. در قطعه کد زیر دو نوع رجیستر ایجاد شده است: کوانتومی وکلاسیک. رجیسترهای کلاسیک برای ذخیره‌سازی نتایج اندازه‌گیری رجیسترهای کوانتومی مورد استفاده قرار می‌گیرند. رجیسترهای کوانتومی همان کیوبیت‌های ما هستند و آن‌ها را در برنامه خود دستکاری خواهیم کرد تا به تأثیرات مطلوب خاص خود برسیم. مدار کوانتومی برای سیم‌کشی کیوبیت‌ها و عملیات‌های مختلف مورد استفاده واقع شده‌اند. شما می‌توانید رونوشتی از کدی که در این مقاله استفاده کرده‌ایم را در این آدرس گیت‌هاب مشاهده کنید.

from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister

from qiskit import available_backends, execute

# Create three quantum and classical registers

q = QuantumRegister(3)
c = ClassicalRegister(3)
qc = QuantumCircuit(q, c)

مقدمه

پیش از آن که وارد مسیر آشنایی با دورنوردی کوانتومی ‌شویم، ابتدا می‌بایست معنی یک کپی یا کلون از کیوبیت را بدانیم. همان طور که در ادامه خواهیم دید، کیوبیت‌ها در وضعیت‌های نامشخص به طور کلی نمی‌توانند کپی یا کلون شوند. بنابراین احتمالاً به طور طبیعی از خود می‌پرسید که اگر نتوانیم یک کیوبیت را کپی یا کلون کنیم، چگونه می‌توانیم آن را انتقال دهیم؟ در این مقاله نشان خواهیم داد که چگونه می‌توانیم این محدودیت را به طور مطمئنی برای ارسال یک کیوبیت بدون فقدان اطلاعات دور بزنیم.

فیلم آموزش سیستم های کوانتومی درهم تنیده در فرادرس

کلیک کنید

اگر از قبل با مکانیک کوانتومی آشنا باشید، مسلماً نمادگذاری دیراک و برداری وضعیت‌های پایه |0⟩ و |1⟩ و همچنین توضیح عمومی یک کیوبیت به صورت ترکیب خطی از وضعیت‌های پایه را به خاطر می‌آورید. این مفاهیم در نمودار زیر مشخص هستند:

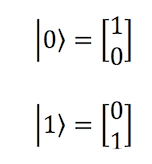
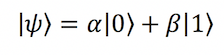
قضیه عدم کلونینگ

مسیر آشنایی‌مان با دورنوردی کوانتومی را در ابتدا با توضیح نمادگذاری کلونینگ کیوبیت‌ها آغاز می‌کنیم. «قضیه عدم کلونینگ» بیان می‌کند که شما نمی‌توانید به طور سراسری یک کیوبیت را که در وضعیت کوانتومی نامشخص قرار دارد، کلون کنید. در ادامه این گزاره راکمی عمیق‌تر بررسی می‌کنیم تا دلیل درستی آن را دریابیم.

پیش از آن که وارد این موضوع شویم لحظه‌ای وقت خود را صرف نگاه به قواعد جمع و ضرب بردارها می‌کنیم، چون برای درک «قضیه عدم کلونینگ» به این مفاهیم نیازمند هستیم.

|?⟩,|?⟩, و |?⟩ بردار هستند

مجموع |?⟩ + |?⟩ یک بردار است

ضرب اسکالر ?|?⟩ یک بردار است و ? یک عدد مختلط است که ? ∈ ℂ

جمع خاصیت جابجایی دارد: |?⟩ + |?⟩ = |?⟩ + |?⟩

جمع خاصیت شرکت‌پذیری دارد: (|?⟩ + |?⟩) + |?⟩ = |?⟩ + (|?⟩ + |?⟩)

ضرب اسکالر خاصیت توزیع‌پذیری برای اسکالرها و بردارها دارد:

(? + ?)|?⟩ = ?|?⟩ + ?|?⟩ where ?,? ∈ ℂ

?(|?⟩ + |?⟩) = ?|?⟩ + ?|?⟩ که ? ∈ ℂ

ضرب اسکالر شرکت‌پذیر است:

?(?|?⟩) = (??)|?⟩ که ?,? ∈ ℂ

اینک تصور کنید که بتوانیم یک عملگر همانی خاص ایجاد کنیم که آن را U می‌نامیم و این عملگر بتواند یک کیوبیت را کلون کند. این عملگر دو کیوبیت به عنوان ورودی می‌گیرد که یکی در وضعیت نامشخص |?⟩ و دیگری در وضعیتی مانند |0⟩ است و به عنوان هدف ما برای کپی کردن عمل می‌کند. سپس عملگر کلونینگ یک رونوشت از کیوبیت ما به همراه کیوبیت اصلی اولیه تأمین می‌کند و هر دو کیوبیت در همان وضعیت |?⟩ هستند.

بنابراین اجازه بدهید عملگر کلونینگ خودمان را تست کنیم و ببینیم که وقتی از آن استفاده کنیم چه می‌شود؟ می‌دانیم که اگر عملگر کلونینگ خود را استفاده کنیم، در نهایت می‌توانیم یک کپی و یک کیوبیت اصلی خودمان را داشته باشیم که در شکل زیر نشان داده شده است.

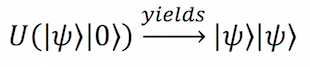
به خاطر داشته باشید که یک کیوبیت تنها یک برهم‌نهی از وضعیت‌های |?⟩ = α|0⟩+β|1⟩ است. بنابراین اجازه بدهید پیش‌تر برویم و |?⟩ را با α|0⟩+β|1⟩ عوض کنیم و سپس حاصل‌ضرب را مانند فرمول زیر به دست می‌آوریم:

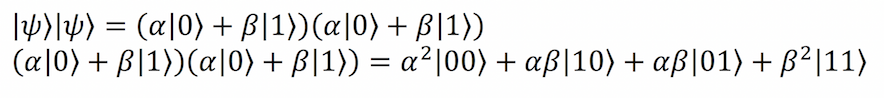
اینک سؤال این است که اگر بسط |?⟩ را کلون کنیم، ماشین کلونینگ ما چه کار می‌کند؟ بنابراین در ادامه این وضعیت را بررسی می‌کنیم تا ببینیم چه چیزی به دست می‌آوریم.

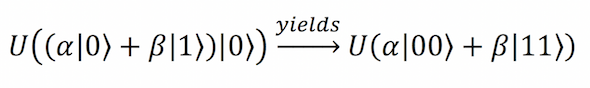
که همان فرمول زیر است:

نتایج دو عملگر کلونینگ خودمان را مقایسه می‌کنیم:

• α²|00⟩ + αβ|10⟩ + αβ|01⟩ + β²|11⟩
• α|00⟩ + β|11⟩

همان طور که می‌بینید، نتایج یکسان نیستند. چگونه می‌توان این وضعیت را درست کرد؟ پاسخ ساده این است که همانند تصور زیر، نمی‌توان درست کرد.

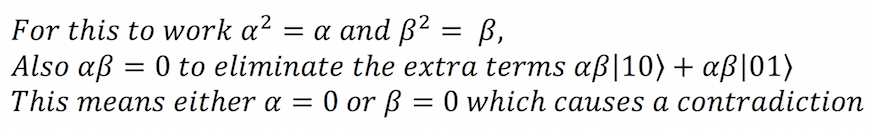
اینک با یک تناقض مواجه می‌شویم که یا مکانیک کوانتوم علی‌رغم سال‌ها تجربیات عینی نادرست است و یا این که ما نمی‌توانیم کیوبیت‌هایی را که در وضعیت ناشناس هستند به طور قابل اطمینانی کلون کنیم. واقعیت تلخ این است که مهم نیست چه قدر تلاش کنیم، چون در هر صورت نمی‌توانیم کیوبیت‌هایی را که در وضعیت‌های کوانتومی ناشناس هستند کلون کنیم.

با این حال نکته ظریفی وجود دارد که باید به آن اشاره کنیم. «قضیه عدم کلونینگ» نمی‌گوید که کیوبیت‌ها نمی‌تو‌انند در وضعیت کوانتومی یکسانی باشند. این قضیه صرفاً بیان می‌کند که اگر شما واقعیت آن‌ها را ندانید، در این صورت نمی‌توانید ماشینی بسازید که آن‌ها را به طور مطمئنی کلون کند. در دنیا منعی برای حضور کیوبیت‌های دارای وضعیت یکسان وجود ندارد.

کپی کردن کیوبیت‌ها

سؤالی که در این مرحله پیش می‌آید این است که اگر ما وضعیت کیوبیت‌ها را از قبل بدانیم، آیا می‌توانیم آن‌ها را کلون کنیم؟ پاسخ مثبت است. برای مثال اگر بدانیم که باید یک کیوبیت را کلون کنیم که در یکی از دو وضعیت برهم‌نهی ممکن یعنی |+⟩ یا |−⟩  .قرار خواهد داشت، در این صورت می‌توانیم چند تبدیل همانی اجرا کنیم که به ما امکان می‌دهد تا وضعیت کیوبیت را کپی کنیم

فیلم آموزش مکانیک کوانتومی ۱ در فرادرس

کلیک کنید

به خاطر بیاورید که تبدیل آدامار (Hadamard transform) برای این استفاده می‌شود که یک کیوبیت را بسته به این که عملگر در کدام یک از وضعیت‌های پایه |0⟩ یا |1⟩ روی کیوبیت اعمال شده است، آن‌ها را در یکی از وضعیت‌های برهم‌نهی |+⟩ یا |−⟩ قرار دهد. در بردار حاصل وقتی به اندازه‌گیری کوانتوم بپردازیم، احتمال برابری برای بازگرداندن هر یک از مقادیر 1 یا 0 وجود خواهد داشت. نمودارهای زیر تعریف |+⟩ و |−⟩ و همچنین مدار کوانتومی مورد نیاز برای تولید آن‌ها را ارائه کرده است.

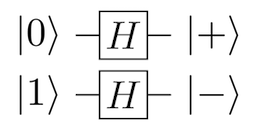
ما چگونه می‌توانیم وضعیت یک کیوبیت را کپی کنیم؟ می دانیم که دو وضعیت برهم‌نهی |+⟩ و |−⟩ باید از یکی از وضعیت‌های پایه |0⟩ یا |1⟩ تولید شوند. این بدان معنی است که ما باید کیوبیت را از یکی از وضعیت‌های |+⟩ و |−⟩ برهم‌نهی بگیریم و سپس کیوبیت ما در یکی از وضعیت‌های پایه |0⟩ یا |1⟩ خواهد بود.

با به‌کارگیری تبدیل آدامار می‌توانیم به راحتی کیوبیت خود را از وضعیت برهم‌نهی به دست آوریم. به خاطر داشته باشید که تبدیل کوانتوم معکوس‌پذیر است و از این رو با به‌کارگیری همین تبدیل آدامار همانی می‌توانیم تبدیل آدامار قبلی را به طور معکوس اجرا کنیم. نمودار زیر را ببینید.

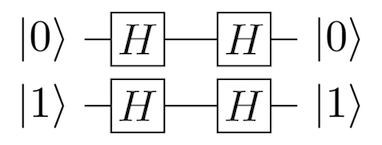
زمانی که کیوبیت از حالت برهم‌نهی به دست آمد، می‌توانیم یک not کنترل شده (CNOT) بین کیوبیت اصلی خودمان که می‌خواهیم کپی کنیم و کیوبیت هدف قرار دهیم تا کیوبیت اصلی به عنوان کنترلی برای کیوبیت هدف عمل کند. به یاد داشته باشید که عملگر CNOT یک تبدیل همانی 2 کیوبیتی است که در آن یک کیوبیت به عنوان کنترل و دیگری به عنوان هدف عمل می‌کند. اگر کیوبیت کنترل برابر با 1 تعیین شده باشد، در این صورت کیوبیت هدف معکوس شده است.

اینک که هر دو کیوبیت را در وضعیت‌های پایه یکسان |0⟩ یا |1⟩ داریم، می‌توانیم یک تبدیل آدامار برای قرار دادن هر دو کیوبیت در وضعیت برهم‌نهی یکسان |+⟩ یا |−⟩ اجرا کنیم. نمودار مدار زیر یک سری از تبدیل‌های همانی را نشان می‌دهد که برای کپی کردن یک کیوبیت در وضعیت |+⟩ اجرا شده‌اند.

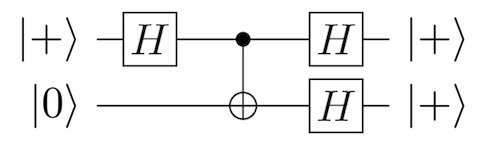
در ادامه کد QISKit برای اجرای عملیات کپی کردن ارائه شده است.

# Create an initial superposition + state
qc.h(q[0])

# Take the qubit out of superposition
qc.h(q[0])

# Perform a CNOT between the qubits
qc.cx(q[0], q[1])

# Put the qubits into superposition and now the states are the same
qc.h(q[0])
qc.h(q[1])

ارتباط کوانتومی

با توجه به محدودیت‌ها و قیودی که در مورد کلون کردن کیوبیت‌ها وجود دارد، ممکن است از خود بپرسید آیا ما می‌توانیم راهی بیابیم که بین وضعیت‌های کیوبیت‌های نامشخص بر اساس مشخصات پایه‌ای محاسبات کوانتومی ارتباطی برقرار سازیم؟ فرض کنید آلیس یک کیوبیت را در یک وضعیت کوانتومی نامشخص به صورت |?⟩ = α|0⟩ + β|1⟩ دارد و انتظار دارد با همکار خود به نام باب ارتباط برقرار کند. این کار به چه طریقی میسر است؟ تصور کنید ما بتوانیم به روشی یک پیوند جادویی بین کیوبیت آلیس و یک کیوبیت که باب در وضعیت پایه |0⟩ آماده کرده است، برقرار کنیم.

فیلم آموزش نظریه میدان کوانتومی ۱ در فرادرس

کلیک کنید

این چه نوع پیوند خاصی است که آلیس می‌تواند ایجاد کند؟ تصور کنید که می‌توانستیم یک گیت CNOT را بین کیوبیت او و کیوبیت باب ایجاد کنیم که می‌توانست تا هر گستره‌ای را پوشش دهد. این وضعیت در نمودار زیر قابل مشاهده است. می دانیم که ایجاد چنین گیتی ناممکن است؛ اما تصور کنید می‌توانستیم یک گیت CNOT بیت این کیوبیت‌ها ایجاد کنیم تا نتیجه آن را ببینیم.

می‌توانیم ببینیم که پس از این که از گیت CNOT استفاده کردیم، وضعیت الحاقی اینک به صورت |?⟩ = α|00⟩ + β|11⟩ است. بنابراین چه می‌شود اگر آلیس کیوبیت خود را به صورت①در وضعیت پایه |0⟩ و |1⟩ اندازه‌گیری کند؟ در این حالت وی مقدار 0 یا 1 را به دست می‌آورد و وضعیت الحاق جدید به صورت |00⟩ یا |11⟩ خواهد بود که باعث می‌شود کیوبیت باب به صورت②در وضعیت |0⟩ یا |1⟩ باشد و در نتیجه این همان وضعیت α|0⟩ + β|1⟩ نیست. بنابراین انجام چنین اندازه‌گیری‌هایی مسلماً به برقراری ارتباط بین آلیس و باب کمک نخواهد کرد.

آیا آلیس گزینه دیگری در اختیار دارد؟ چه می‌شود اگر آلیس بخواهد کیوبیت ① خود را در وضعیت‌های پایه |+⟩ و |-⟩ اندازه‌گیری کند؟ برای این کار می‌توانیم |0⟩ و |1⟩ را بر حسب |+⟩ و |-⟩ بنویسیم، چنان‌که در ادامه نمایش داده شده است.

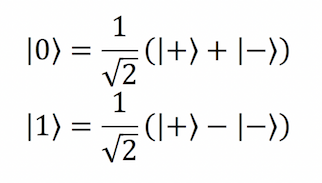
اینک پیش‌تر می‌رویم و کیوبیت ① آلیس را بر حسب |+⟩ و |-⟩ بازنویسی می‌کنیم که در ادامه نمایش یافته است.

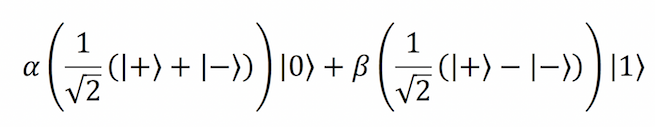
عبارت فوق را با جمع زدن جملات به صورت زیر ساده‌سازی می‌کنیم:

می‌توانیم ببینیم که اگر آلیس بخواهد کیوبیت ① خود را اندازه‌گیری کند، مقادیر + یا – به دست خواهد آورد و کیوبیت باب در وضعیت α|0⟩ + β|1⟩ یا α|0⟩ − β|1⟩ خواهد ماند.

در حالتی که آلیس کیوبیت ① خود را اندازه‌گیری کند و یک + به دست آورد، در این صورت باب نیاز ندارد در مورد کیوبیت ② خودش کاری انجام دهد، چون به طور دقیق وضعیت آن به صورت α|0⟩ + β|1⟩ است. با این حال اگر آلیس کیوبیت خود را به صورت – اندازه‌گیری کند در این صورت کیوبیت باب از فاز α|0⟩ − β|1⟩ خارج شده است.

باب می‌تواند فاز کیوبیت خود را تغییر دهد تا وضعیت دقیق α|0⟩ + β|1⟩ را به دست آورد. باب این کار را با استفاده از گیت پائولی زِد (Pauli Z) انجام می‌دهد. به‌کارگیری گیت Z باعث می‌شود که فاز کیوبیت باب معکوس شود. اگر بخواهید اطلاعات بیشتری در مورد گیت‌های پائولی کسب کنید به این لینک مراجعه نمایید. از این رو تنها کاری که آلیس باید انجام دهد این است که به باب بگوید حاصل اندازه‌گیری‌اش + یا - بوده است. سپس باب در صورت نیاز از انتقال فاز گیت Z برای اصلاح فاز خود استفاده می‌کند که در شکل زیر نمایش یافته است.

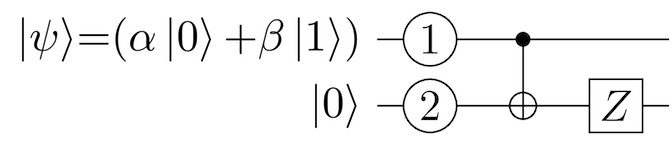
آلیس چگونه می‌تواند اندازه‌گیری خود را در پایه |0⟩ و |1⟩ انجام دهد و بتواند بگوید که حاصل اندازه‌گیری‌اش + بوده است یا -؟ پاسخ این است که آلیس از گیت H آدامار در مورد کیوبیت ① خود استفاده می‌کند تا اندازه‌گیری‌اش را انجام دهد. این وضعیت در شکل زیر نمایان است.

گیت آدامار مقدار + را در اندازه‌گیری 0 و مقدار - را در اندازه‌گیری 1 منعکس می‌کند. به خاطر بسپارید که وقتی آلیس مشغول اندازه‌گیری است در واقع کیوبیت خود را تخریب می‌کند؛ اما وضعیت کیوبیت وی به کیوبیت باب انتقال می‌یابد. کد زیر نشان می‌دهد که چگونه می‌توانیم در مبنای + و – اندازه‌گیری کنیم و یک انعکاس فاز را در صورت لزوم اجرا نماییم.

# Prepare an initial state for qubit ① using a single unitary
qc.u1(0.5, q[0])

# Perform a CNOT between qubit ① and qubit ②
qc.cx(q[0], q[1])

# Measure qubit ① in the + - basis
qc.h(q[0])
qc.measure(q[0], c[0])

# If needed Perform a phase correction to qubit ②
if c[0] == 1:
qc.z(q[1])

بنابراین نتیجه همه این‌ها در مورد انتقال کیوبیت چه می‌تواند باشد؟ نتیجه بحث‌های فوق این است که اگر روشی برای ایجاد یک CNOT راه دور بین کیوبیت آلیس و کیوبیت باب داشته باشیم، می‌توانیم بین آن دو ارتباطی برقرار سازیم. خبر خوب این است که برای انجام این کار روشی می‌شناسیم و آن از طریق در‌هم‌تنیدگی است. اینک اجازه بدهید ببینیم چگونه می‌توانیم از یک در‌هم‌تنیدگی برای ایجاد بین عملیات CNOT راه دور و دورنوردی (تله پورت) یک کیوبیت اجرا کنیم.

دورنوردی کوانتومی

شیوه کار چگونه است؟ کاری که قصد داریم انجام دهیم این است که یک وضعیت خاصی از درهم‌تنیدگی بین سه کیوبیت ایجاد کنیم که در آن یکی از کیوبیت‌های ما اطلاعات نامشخصی را نگه‌داری می‌کند که می‌خواهیم ارسال کنیم و دوتای دیگر یک جفت درهم‌تنیده هستند که بین فرستنده و گیرنده اطلاعات به اشتراک گذارده می‌شود.

فیلم آموزش محاسبات کوانتومی در فرادرس

کلیک کنید

یک سری اندازه‌گیری‌ها روی دو کیوبیت انجام می‌دهیم و در نهایت آن‌ها را از وضعیت درهم‌تنیده خارج می‌کنیم. این اندازه‌گیری‌ها و دانش ما از وضعیت‌های درهم‌تنیده به ما امکان می‌دهد که کیوبیت اصلی خودمان را به مقصدی تله‌پورت کنیم، بدون این که اطلاعات آن از دست برود. با این حال کیوبیت اصلی که حاوی اطلاعاتی است که می‌خواهیم در طی بخشی از پروتکل دو حالتی خود ارسال کنیم تخریب می‌شود.

راه‌اندازی وضعیت اولیه

در سناریوی‌مان یک بار دیگر فرض خواهیم کرد که آلیس می‌خواهد کیوبیتی به باب بفرستد که در یک وضعیت نامشخص است. می دانیم که آلیس نمی‌تواند به طور مستقیم کیوبیت را کلون کند، زیرا «قضیه عدم کلونینگ» مانع اوست. با این حال آلیس یک کدکننده بسیار باهوش کوانتوم است و می‌داند که می‌تواند از ماهیت درهم‌تنیدگی کوانتومی برای به رسیدن به هدف خود کمک بگیرد.

نخستین کاری که آلیس انجام می‌دهد این است که از دوست خود ایوا (Eve) برای برقراری ارتباط بین خود و باب کمک می‌خواهد. او از ایوا می‌خواهد که یک جفت کیوبیت درهم‌تنیده برای او و باب آماده کند و به ایوا آموزش می‌دهد تا یکی از کیوبیت‌ها را به او و دیگری را به باب بدهد. این وضعیت در نمودار زیر قابل مشاهده است.

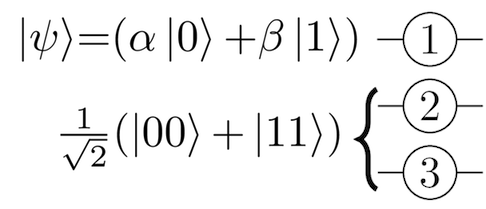
در نمودار مدار زیر می‌بینیم که کیوبیت دارای برچسب ① کیوبیتی است که اطلاعات نامشخصی دارد و آلیس می‌خواهد که آن را به باب تله‌پورت نماید. کیوبیت‌هایی که دارای برچسب ② و ③ هستند، کیوبیت‌های درهم‌تنیده محسوب می‌شوند که ایوا برای آلیس و باب آماده کرده است. وضعیت الحاق این سیستم 3 کیوبیتی به سادگی حاصل‌ضرب کیوبیت‌ها است که در ادامه نمایش یافته است.

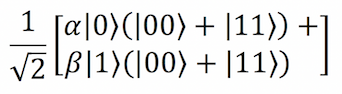
در ادامه کد QISkit برای راه‌اندازی جفت درهم‌تنیده کیوبیت‌ها و وضعیت اولیه کیوبیت‌هایی که می‌خواهیم تله‌پورت کنیم ارائه شده است.

# Prepare an initial state for qubit ① using a single unitary
qc.u1(0.5, q[0])

# Prepare an entangled pair using qubit ② and qubit ③
qc.h(q[1])
qc.cx(q[1], q[2])

# Barrier to prevent gate reordering for optimization
qc.barrier(q)

ایجاد NOT کنترلی از راه دور و اعمال اصلاح

اینک که کیوبیت‌هایمان آماده هستند، کار بعدی که آلیس باید انجام دهد این است که یک عملیات CNOT بین کیوبیت ① که می‌خواهد به باب تله‌پورت کند و نیمه خودش از جفت درهم‌تنیده کیوبیت ② که با باب به اشتراک گذاشته است اجرا کند. این وضعیت در نمودار مدار زیر قابل مشاهده است.

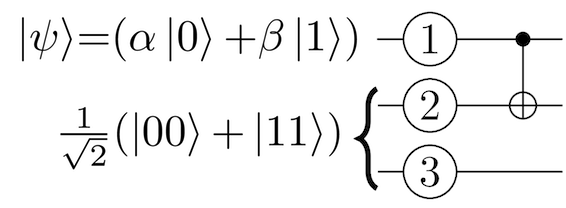
در ادامه به بررسی تأثیر عملیات CNOT بر روی وضعیت الحاق سیستم 3 کیوبیتی می‌پردازیم، که در شکل زیر نمایان است. همان طور که می‌بینید کیوبیت ① به صورت 1 تعیین شده است که به وسیله مثلث سبزرنگ مشخص می‌شود، کیوبیت② هدف، معکوس شده است که به وسیله مثلث قرمزرنگ مشخص است.

این وضعیت چه کمکی به آلیس می‌کند تا بتواند با باب ارتباط برقرار کند؟ در این نقطه چه رخ می‌دهد اگر آلیس بخواهد کیوبیت ② را که در نمودار مدار زیر نمایش یافته است، اندازه‌گیری کند؟

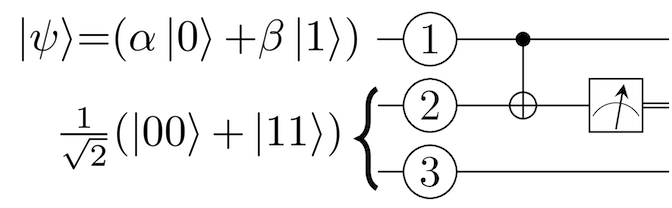
آلیس می‌تواند مقادیر 0 یا 1 به دست آورد. این اندازه‌گیری چه چیزی را برای آلیس مشخص می‌کند؟ نتیجه این اندازه‌گیری آن است که آلیس می‌فهمد وضعیت باقی‌مانده الحاقی کیوبیت‌های ① و ③ در یکی از دو وضعیت ممکن است که در ادامه نمایش یافته است.

به خاطر داشته باشید که آلیس تلاش می‌کند تا وضعیت |?⟩ = α|0⟩ + β|1⟩ را به باب ارسال کند. با این حال وقتی آلیس کیوبیت ② را اندازه‌گیری می‌کند و مقدار 1 به دست می‌آورد، می‌فهمد که کیوبیت ③ به ترتیبی از 0 به 1 معکوس شده است. در این لحظه آلیس این اندازه‌گیری را یادداشت می‌کند و اندازه‌گیری خود را به باب اطلاع می‌دهد. آلیس و باب می‌دانند که می‌توانند به سادگی کیوبیت را با استفاده از گیت پائولی X که در تصویر زیر نمایش یافته است، معکوس نمایند. اگر می‌خواهید اطلاعات بیشتری در مورد عملیات‌های پائولی بیابید به این آدرس مراجعه کنید.

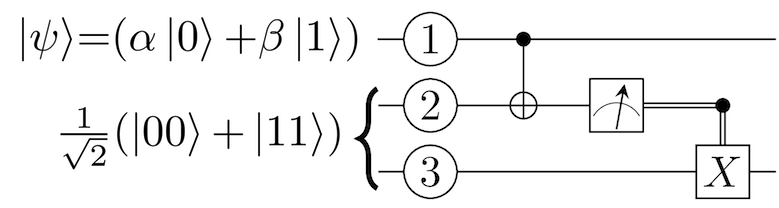
در ادامه کد QISkit برای ایجاد یک CNOT، اندازه‌گیری کیوبیت و اجرای یک معکوس سازی بیت در صورت نیاز ارائه شده است.

# Perform a CNOT between qubit ① and qubit ②
qc.cx(q[0], q[1])

# Measure qubit ② in the computational basis
qc.measure(q[1], c[1])

# If needed Perform a bit flip correction to qubit ③
if c[1] == 1:
qc.x(q[2])

اعمال اصلاح فاز

کار بعدی که آلیس انجام می‌دهد اجرای یک تبدیل آدامار بر روی کیوبیت ① است. او این کار را دقیقاً همانند بار قبلی انجام می‌دهد و بدین ترتیب می‌تواند به باب بگوید که اگر بخواهد می‌تواند یک معکوس سازی فاز بر روی کیوبیت ③ خود انجام دهد که در نمودار مدار زیر نمایش یافته است.

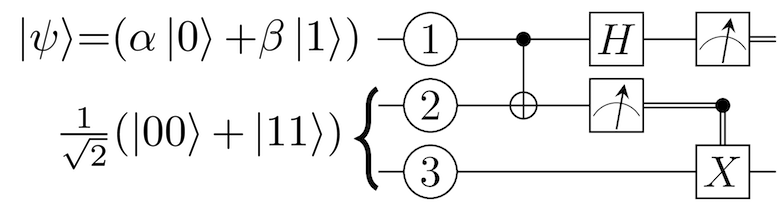
نمودار فوق را کمی بیشتر بررسی می‌کنیم تا ببینیم پس از به‌کارگیری گیت آدامار چه اتفاقی در خصوص سیستم 3 کیوبیتی ما رخ می‌دهد. احتمالاً از مباحثی که از قبل مطرح کردیم به خاطر دارید که استفاده از عملگر آدامار در مورد وضعیت‌های پایه کیوبیت |0⟩ و |1⟩ باعث می‌شود که کیوبیت ما به یک از دو وضعیت برهم‌نهی زیر تبدیل یابد.

اینک دو وضعیت برهم‌نهی برای H|0⟩ و H|1⟩ را در توصیف وضعیت 3 کیوبیتی قبلی خودمان جایگزین می‌کنیم. این حالت در نمودار زیر با مستطیل قرمز مشخص شده است.

اینک حاصل‌ضرب را محاسبه می‌کنیم تا ببینیم وضعیت سیستم 3 کیوبیتی چگونه است. این وضعیت در تصویر زیر گویا است.

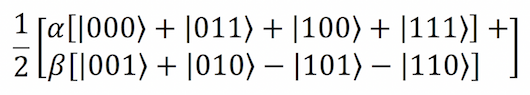
برای این که مشاهده آنچه در حال وقوع است آسان‌تر باشد، نمودار فوق را چنین بازنویسی می‌کنیم که کیوبیت‌های ① و ② را با هم گروه‌بندی می‌کنیم و کیوبیت ③ را جدا نگه می‌داریم. وضعیت فوق در تصویر زیر با مستطیل قرمزرنگ مشخص شده است.

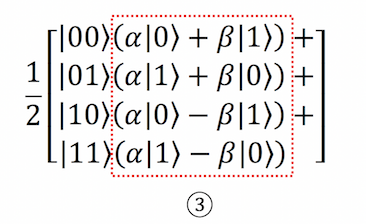
می‌بینیم که کیوبیت ③ در خود همه کیوبیت‌ها را به جز وضعیت اولیه کیوبیت ① دارد. آنچه در عمل انجام داده‌ایم این است که وضعیت را از کیوبیت به کیوبیت تله‌پورت کرده‌ایم. با این حال همچنان یک مشکل باقی‌مانده است.

به یاد داشته باشید که ما در حال تلاش برای تله‌پورت کردن وضعیت کیوبیت ① هستیم که به صورت |?⟩ = α|0⟩ + β|1⟩ است و پیش‌تر وضعیت‌هایی که لازم بوده است کیوبیت خود را معکوس کنیم را بررسی کرده‌ایم. از این رو همه آن چه باید انجام داد این است که مواردی را در نظر بگیریم که باب نیاز دارد فاز کیوبیت خود را با استفاده از گیت Z پائولی معکوس کند.

قبلاً دیدیم که آلیس می‌تواند تعیین کند که آیا یک معکوس سازی فاز برای اندازه‌گیری کیوبیت در مبنای |+⟩ و |-⟩ لازم است یا نه. بنابراین آلیس اندازه‌گیری را پس از به‌کارگیری گیت آدامار انجام می‌دهد که این کار باعث می‌شود وی بتواند وقتی کیوبیت + است مقدار 0 و وقتی – است مقدار 1 را به دست آورد و در این صورت این مقدار را به باب بدهد تا باب بتواند تعیین کند که نیاز به معکوس سازی فاز دارد یا نه. کل این وضعیت در نمودار زیر قابل مشاهده است.

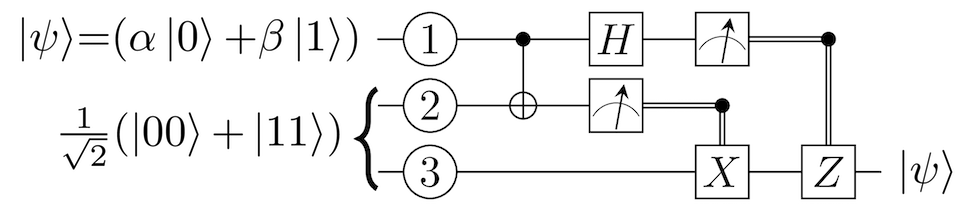
کد QISkit برای اندازه‌گیری کیوبیت در مبنای + - و اجرای اصلاح فاز در صورت نیاز در ادامه ارائه شده است.

# Measure qubit ① in the + - basis
qc.h(q[0])
qc.measure(q[0], c[0])

# If needed Perform a phase correction to qubit ③
if c[0] == 1:
qc.z(q[2])

جمع‌بندی

بدین ترتیب ما موفق به تله‌پورت کردن کوانتوم شده‌ایم. اینک آلیس می‌تواند یک کیوبیت را با موفقیت به باب تله‌پورت کند. چند برداشت مهم در خصوص پروتکل تله‌پورت وجود دارد که می‌بایست به صورت گذرا مورد اشاره قرار دهیم:

• آلیس و باب نمی‌توانند سریع‌تر از سرعت نور با هم ارتباط برقرار کنند. آلیس باید به باب بگوید که دو اندازه‌گیری که انجام داده چیست و این کار می‌بایست از طریق یک کانال ارتباط کلاسیک صورت بگیرد که طبق تعریف، سرعتی کمتر از سرعت نور دارد.
• آلیس در نهایت کیوبیت خود را تخریب می‌کند، زیرا اطلاعات آن را به باب تله‌پورت کرده است و از این رو ما قضیه عدم کلونینگ را نقض نکرده‌ایم.

اگر به این نوشته علاقه‌مند بودید، پیشنهاد می‌کنیم موارد زیر را نیز ملاحظه کنید:

• مجموعه آموزش های فیزیک
• آموزش مکانیک کوانتومی ۱
• بعد چیست و چه ارتباطی با رویدادهای جهان پیرامون ما دارد؟
• آموزش مکانیک کوانتومی ۲
• مجموعه آموزش‌های فنی و مهندسی
• آموزش فیزیک مدرن با رویکرد حل مسئله

==