تابع های پایتون برای محاسبات فیزیک | راهنمای مقدماتی

اگر می‌خواهید در زمینه محاسبات فیزیکی در پایتون به سطح بالاتری گام بگذارید، باید تابع های پایتون برای محاسبات فیزیک را بیاموزید. این مقاله با این دیدگاه نوشته شده است که شما یک فرد فاقد زمینه خاص برنامه‌نویسی و صرفاً علاقه‌مند به فیزیک هستید. با این حال فرض ما این است که قبلاً برخی تجربیات اجرای محاسبات فیزیکی در پایتون دارید، گرچه این محاسبات لازم نیست چندان عجیب و غریب باشند.

شاید از خود بپرسید منظور از تابع چیست؟ در واقع مفهوم تابع در زبان‌های برنامه‌نویسی و به طور خاص پایتون شباهت زیادی به مفهوم ریاضی آن دارد و شکل کلی‌اش به صورت زیر است:

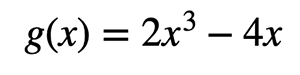
در تابع ریاضی فوق شما می‌توانید هر مقداری را به جای x بگذارید تا مقدار متفاوتی در خروجی ظاهر شود. یک تابع پایتون نیز شباهت زیادی به این حالت دارد. در واقع تابع فوق می‌تواند عملاً یک تابع پایتون باشد. در این صورت شکل آن به صورت زیر خواهد بود:

شاید برنامه فوق، ساده‌ترین و ملال‌انگیزترین برنامه پایتون باشد، اما برای شروع نقطه خوبی محسوب می‌شود.

فیلم آموزش تابع در زبان برنامه نویسی پایتون با مثال (رایگان) در فرادرس

کلیک کنید

در ادامه برخی نکات مهم را فهرست کرده‌ایم:

• تابع باید یک نام یکتا داشته باشد. ما می‌توانیم از نام g استفاده کنیم و تنها شرطش این است که تابع دیگری با نام g وجود نداشته باشد.
• در تعریف تابع، نام متغیرهای ورودی گرفته می‌شود. در این مورد ما از عبارت x استفاده کرده‌ایم، اما این نام می‌تواند هر چیزی باشد که در ادامه در بدنه تابع مورد استفاده قرار می‌گیرد.
• خروجی تابع به صورت return()‎ است. هر چیزی که درون پرانتز قرار گیرد در نتیجه تابع ارائه می‌شود.
• این تابع یک ورودی (x) و یک خروجی دارد، اما تابع‌ها می‌توانند ورودی‌ها و خروجی‌های زیادی به تناسب نیاز داشته باشند.

تابع محاسبه حرکت پرتابه

در این بخش مثال دیگری از یک تابع پایتون را بررسی می‌کنیم. این تابع یک مقدار ورودی به صورت سرعت اولیه یک شیء و ارتفاع آن از سطح زمین را می‌گیرد. این تابع خروجی مسافت (range) را بازگشت می‌دهد که فاصله‌ای است که آن شیء پرتابه طی خواهد کرد.

امکان محاسبه این مسافت با استفاده از یک راه‌حل تحلیلی نیز وجود دارد، اما ما از رویکرد عددی استفاده می‌کنیم.

فیلم مجموعه آموزش برنامه نویسی پایتون Python – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

به عنوان یک مرور سریع در ادامه روش محاسبه مسافت پیموده شده افقی شیء را توضیح می‌دهیم:

• محاسبه خود را با موقعیت و سرعت اولیه شیء آغاز می‌کنیم و از روی سرعت و جرم می‌توانیم گشتاور شیء را محاسبه کنیم.
• حرکت را به بازه‌های زمانی کوچک مثلاً 0.01 ثانیه تقسیم می‌کنیم.
• نیروی روی شیء را محاسبه می‌کنیم. در این مورد تنها یک نیروی ثابت گرانشی وجود دارد.
• می‌توانیم از این نیرو و گشتار کنونی استفاده کنیم و گشتاور جدید را در انتهای بازه زمانی کوتاه خود محاسبه کنیم.
• در نهایت با استفاده از گشتاور محاسبه شده می‌توانیم موقعیت شیء را به‌روزرسانی کنیم.
• این کار را تا زمانی ادامه می‌دهیم که شیء به سطح زمین برسد که معادل y=0 است.

از این رو محاسبه فوق شبیه یک تابع است.

در این بخش کد فوق را توضیح می‌دهیم:

• در خط یک نام تابع را xrange(v0,h,m) گذاشته‌ایم. دلیل اول این است که مطمئنیم range یک تابع در یکی از ماژول‌های glowscript است که بارگذاری کرده‌ایم. سه متغیر به تابع ارسال می‌کنیم که v0 سرعت اولیه است.
• در خط 13 یک حلقه وجود دارد که محاسبات عددی را اجرا می‌کند.
• این حلقه تا زمانی که موقعیت شیء بزرگ‌تر از صفر باشد تکرار می‌شود. از آنجا که موقعیت را به صورت یک بردار تعریف کرده‌ایم، r.y مؤلفه y موقعیت است.
• خطوط 14 و 15 و 16 همگی معادلات برداری هستند. بنابراین P یک بردار و سمت راست نیز یک معادله برداری است.
• خط 18 موقعیت نهایی را بازگشت می‌دهد. این تابع صرفاً مؤلفه‌های اسکالر x موقعیت را دارد، اما می‌توانید آن را نیز مانند r داشته باشید.
• در نهایت خطوط 20 و 21 خروجی تابع را برای مجموعه خاصی از ورودی‌ها پرینت می‌کند.

در ادامه فرض کنید می‌خواهیم زاویه پرتابی را که بیشترین مسافت را تولید می‌کند محاسبه کنیم.

این بخش از همان تابع قبلی استفاده می‌کند گرچه بازه زمانی را از 0.01 به 0.001 تغییر داده‌ایم. توضیح این بخش به صورت زیر است:

• خطوط 20 تا 24 صرفاً شرایط اولیه هستند. جرم در عمل تغییر نمی‌یابد، اما در ادامه از آن استفاده خواهیم کرد. ضمناً باید سرعت پرتاب را برحسب بزرگی و جهت در نظر بگیریم، اما پیش از فراخوانی تابع به یک بردار تبدیل می‌کنیم.
• خط 22 گام زاویه است. ما می‌خواهیم این تابع را برای برخی زوایای پرتاب اولیه فراخوانی کرده و سپس آن را برای زاویه کمی تندتر تکرار کنیم.
• خطوط 26 و 27 صرفاً برای تنظیم گراف هستند.
• خطوط 29 تا 33 شامل حلقه‌ای است که تابع را با زوایای پرتاب مختلف اجرا می‌کند. این بخش شامل یافتن بردار سرعت پرتاب و کد ترسیم است.

خروجی به صورت زیر است:

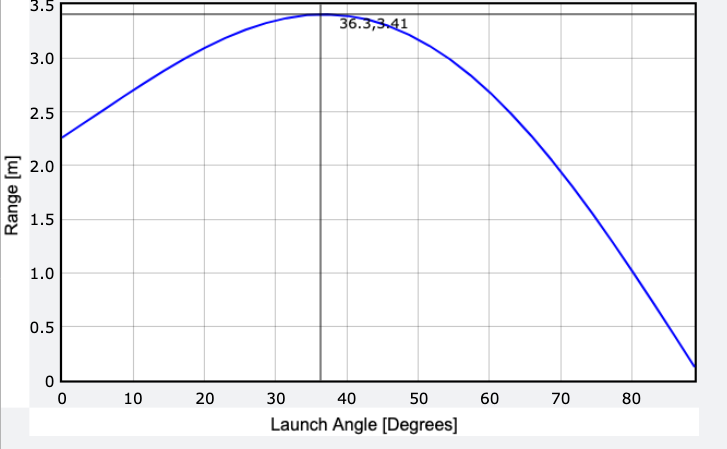
توجه کنید که بیشینه مسافت در زاویه 36 درجه و نه 45 درجه به دست می‌آید. به خاطر دارید که بیشینه مسافت یک پرتابه تنها زمانی در زاویه 45 درجه به دست می‌آید که شیء از روی یک سطح مسطح به همان سطح پرتاب شود. در این مورد ما شیء را از 1 متر بالاتر از سطح زمین پرتاب می‌کنیم. برای پرینت بیشینه مسافت باید از متد پیچیده‌تری استفاده کنید، اما تماشای گراف نیز کاملاً گویا است.

کدهای برنامه

در ادامه، تمامی کدهای استفاده شده در این مطلب را آورده‌ایم. لازم به ذکر است که برای اجرای کدها می‌توانیم به وب‌سایت «+» مراجعه کنیم.