مثلث پاسکال در جاوا اسکریپت – به زبان ساده
در این نوشته قصد داریم یک مثلث پاسکال در جاوا اسکریپت ایجاد کنیم. صورت مسئله چنین است که با فرض وجود یک عدد صحیح غیر منفی numRows، تعداد numRows اول مثلث پاسکال را ایجاد کنید. چنان که میدانیم مثلث پاسکال مثلثی است که در آن هر عدد مجموع دو عدد بالای خودش است.
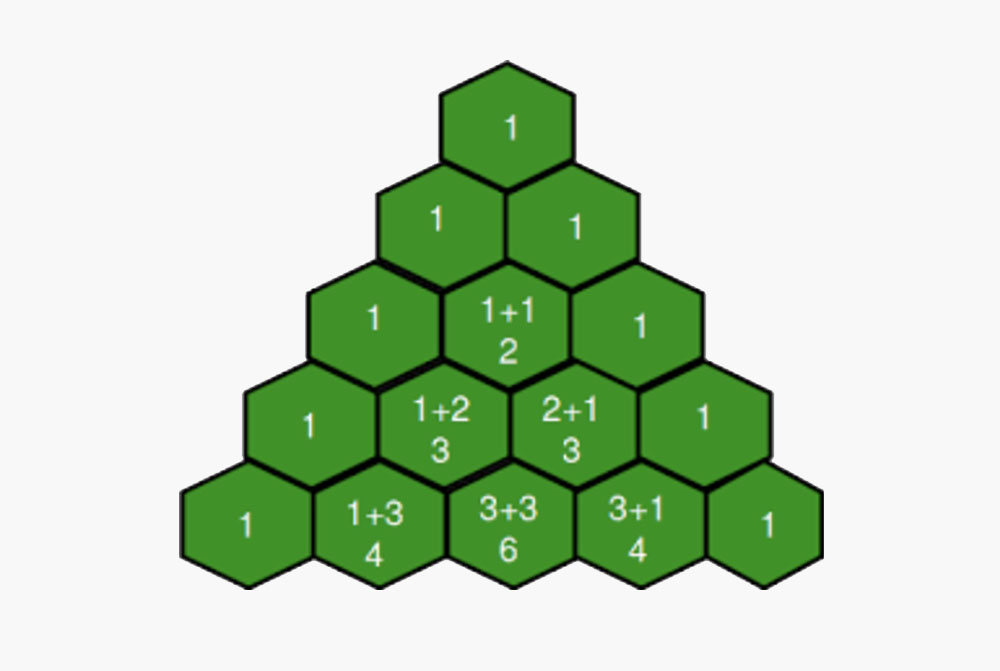
مثال

برای ساخت این مثلث باید به چند نکته توجه داشته باشیم:
- هر ردیف با عدد 1 آغاز و خاتمه مییابد.
- درون هر ردیف، بین 1-ها، هر رقم مجموع دو رقم است که درست بالای آن قرار دارند.
- میتوانیم از این الگو برای ساخت ردیفهای جدید با آغاز از 3 استفاده کنیم، اما با این الگو نمیتوانیم ردیفهای اول و دوم را بسازیم.
- هر ردیف بازنمایی از یک آرایه است و ما باید کل مثلث را در یک آرایه از این ردیفها (در واقع آرایهای از آرایهها) ارائه کنیم.
راهحل گام به گام
هر زمان که روی الگوریتمها کار میکنید، باید مسئله را تا جای ممکن به مسائل کوچکتر تقسیم کنید. در این مورد به جای این که در مورد ساخت کل مثلث نگران باشیم، باید روی وظیفه آسانتری تمرکز کنیم. اینک سؤال این است که اگر بدانیم ردیف قبلی چگونه است، چگونه میتوانیم ردیف بعدی را بسازیم؟
ما حالتهای استثنایی را در انتها بررسی میکنیم. فعلاً فرض میکنیم که دست کم 3 ردیف از مثلث را ساختهایم. از آنجا که الگوی ما با آغاز از ردیف 3 کار میکند، دو ردیف اول مثلث را خودمان میسازیم.
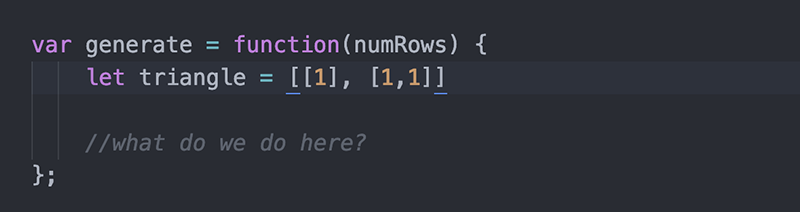
اکنون روش ساخت ردیف سوم را بررسی میکنیم:
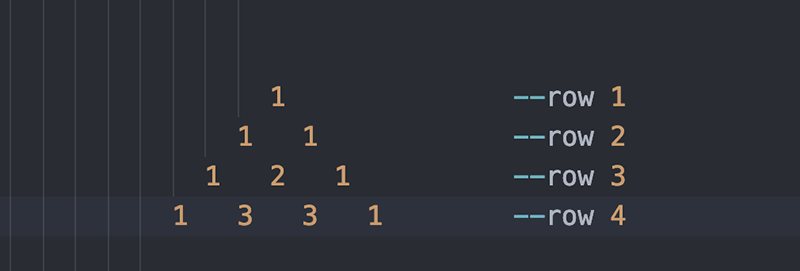
برای محاسبه مقدار میانی ردیف سوم، باید به ردیف دوم دسترسی داشته باشیم. به طور خاص باید به هر دو رقم ردیف دوم دسترسی داشته باشیم تا بتوانیم رقم میانی ردیف سوم را محاسبه کنیم.
برای تولید ردیف چهارم از ردیف سوم نیز کار خود را با درک عدد یک در ابتدا و انتها آغاز میکنیم. برای محاسبه رقم 3 اول، ارقام اول و دوم ردیف قبلی را با هم جمع میکنیم. برای محاسبه 3 دوم، ارقام دوم و سوم ردیف قبلی را با هم جمع میکنیم.
بنابراین در هر ردیف، مهم نیست که طولش چه قدر باشد باید از یک شروع کنیم و روی ردیف قبلی حلقهای تعریف کنیم که ارقام میانی را محاسبه کنیم و سپس به انتها 1 را اضافه کنیم.
تعداد تکرار حلقه چقدر است؟
تعداد تکرار حلقه به تعداد ارقامی است که باید محاسبه کنیم. در مورد ردیف چهارم که چهار رقم دارد، از آنجا که اعداد اول و آخر را میدانیم تنها باید دو رقم را محاسبه کنیم. در مورد ردیف پنجم باید 3 رقم را محاسبه کنیم و همین طور تا آخر.
از آنجا که روی حلقه سوم میچرخیم تا ارقام میانی ردیف چهارم را پیدا کنیم، میتوانیم بگوییم که باید روی ردیف سوم دو بار بچرخیم که یک واحد کمتر از طول آن یعنی 3 است. بنابراین تعداد حلقهها یعنی i باید کمتر از طول ردیف قبلی باشد.
پس از اجرای حلقه یک واحد به انتهای ردیف اضافه میکنیم.
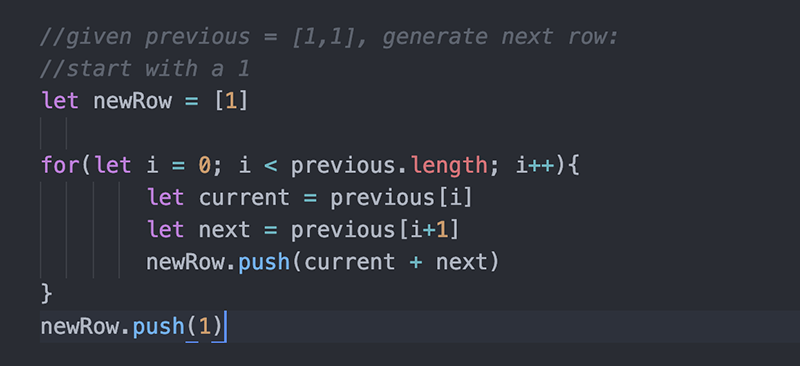
اکنون که با منطق ایجاد ردیف جدید از ردیفهای قبلی آشنا شدیم، آن را درون تابع به خصوصی قرار میدهیم که یک مثلث به عنوان ورودی میگیرد و previous را به عنوان آخرین ردیف مثلث تعریف میکند:
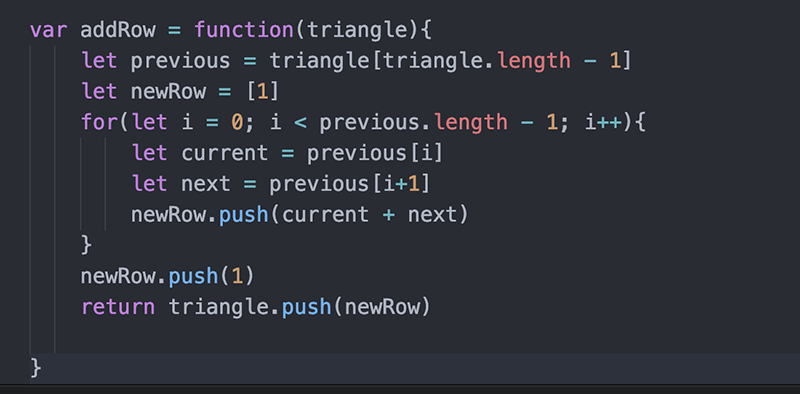
سپس این تابع را از تابع اصلی خود فراخوانی میکنیم:
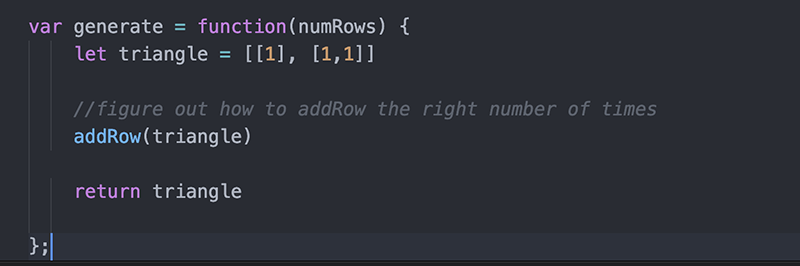
اینک سؤال این است که addRow(triangle) را باید چند بار اجرا کنیم و این کار را چگونه انجام میدهیم؟
پاسخ دادن به سؤال نخست آسان است. فرض کنید numRows برابر با 10 است. با 2 ردیف کار خود را آغاز میکنیم. بنابراین باید 8 ردیف دیگر ایجاد کنیم که numRows منهای 2 است.
پاسخ دادن به سؤال بعدی در Ruby آسانتر است. اگر به روبی علاقهمند باشید، میدانید که متد جالبی برای کارهای تکراری دارد.
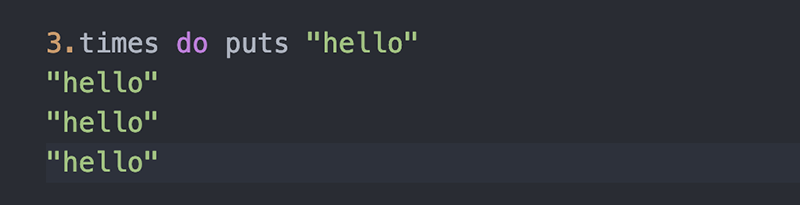
در جاوا اسکریپت این کار با حلقه for قابل اجرا است:
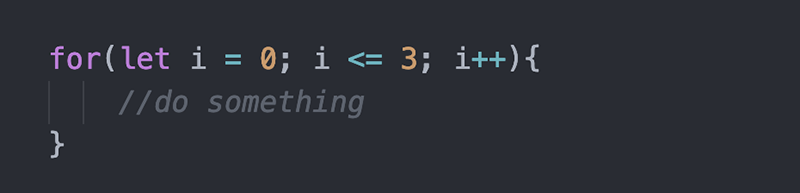
که نتیجه زیر را به دست میدهد:
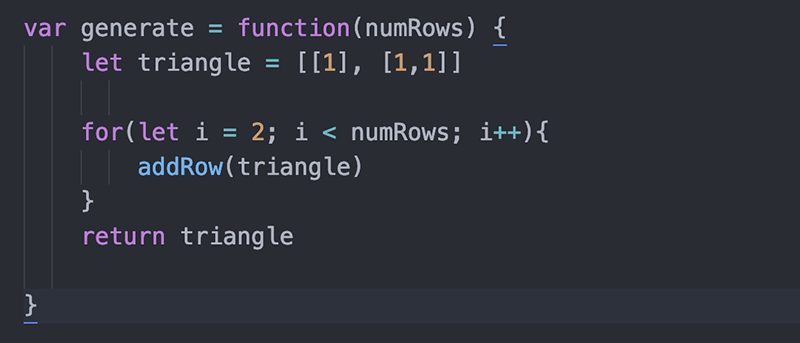
حالتهای استثنایی را فراموش نکنید
اینک باید به مدیریت حالتهای استثنایی بپردازیم. تابع ما فرض میکند که ما باید حداقل سه ردیف بسازیم، اما گر عدد ورودی کمتر از سه باشد چطور؟
اگر عدد ورودی 0 باشد، باید هیچ مثلثی بازگشت ندهیم، یعنی یک آرایه خالی [] بازگشت مییابد. اگر عدد ورودی 1 باشد، باید ردیف نخست یعنی [[1]] را بازگشت دهیم. اکنون کد کامل به صورت زیر درآمده است:
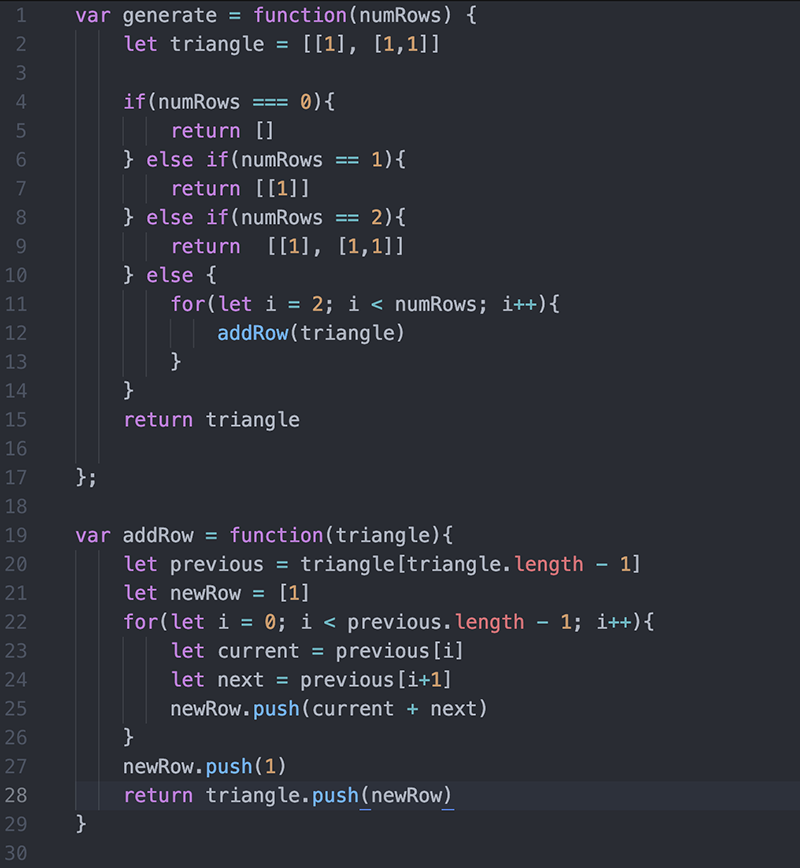
البته این کوتاهترین راهحل ممکن نیست، اما درک آن آسان است و عملکرد مناسبی دارد.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای برنامهنویسی جاوا اسکریپت
- آموزش قضیه بسط دو جمله ای و مثلث خیام
- مجموعه آموزشهای برنامهنویسی
- برنامه محاسبه مثلث خیام پاسکال — راهنمای کاربردی
- جاوا اسکریپت چیست؟ - به زبان ساده
==