فرادرسالگوریتم پریم در جاوا — راهنمای جامع
در این مقاله ابتدا با مفهوم درخت‌های پوشای کمینه آشنا می‌شویم. سپس از الگوریتم پریم در جاوا برای یافتن چنین درختی استفاده می‌کنیم.
درخت پوشای کمینه
منظور از «درخت پوشای کمینه» (minimum spanning tree) یا به اختصار MST یک گراف وزن‌دار، غیر جهت‌دار و همبند است که وزن کلی یال‌های آن با حذف یال‌های سنگین‌تر به کمترین مقدار ممکن رسیده باشد. به بیان دیگر ما همه رئوس گراف را دست‌نخورده حفظ می‌کنیم، اما ممکن است برخی یال‌ها را حذف کنیم به طوری که مجموعه وزن همه یال‌ها به کمینه مقدار برسد.
کار خود را با یک گراف وزن‌دار آغاز می‌کنیم، زیرا کمینه‌سازی وزن کلی یال در صورتی که این یال‌ها کلاً وزنی نداشته باشند، معنی نخواهد داشت. در تصویر زیر مثالی از این نوع گراف می‌بینید:
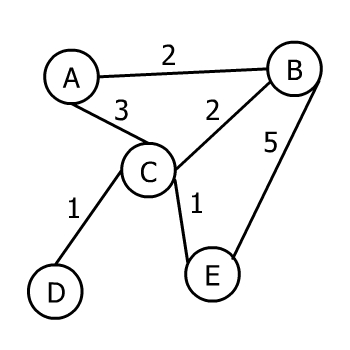
گراف فوق وزن‌دار، غیر جهت‌دار و همبند است. MST این گراف به صورت زیر است:
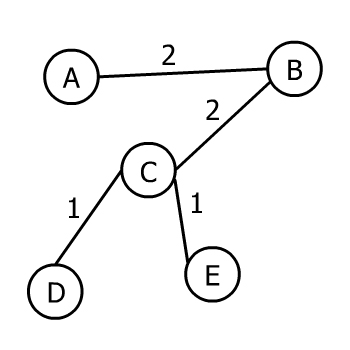
توجه کنید که درخت پوشای کمینه گراف، یکتا نیست. از این رو اگر گراف بیش از یک MST داشته باشد، هر MST وزن یال مجموع یکسانی خواهد داشت.
الگوریتم پریم
الگوریتم پریم (Prim) یک گراف وزن‌دار، غیر جهت‌دار و همبند به عنوان ورودی می‌گیرد و یک MST از گراف به عنوان خروجی بازگشت می‌دهد. این الگوریتم به روش حریصانه کار می‌کند. در گام نخست یک رأس دلخواه انتخاب می‌شود، سپس در هر گام جدید نزدیک‌ترین رأس به درختی که تا اینجا ساخته شده اضافه می‌شود تا این که هیچ رأس غیر همبندی نماند. در ادامه الگوریتم پریم را روی گراف مثال فوق به صورت گام به گام اجرا می‌کنیم:
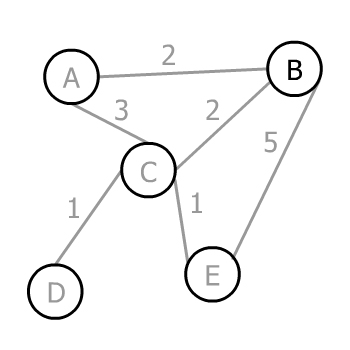
با فرض رأس دلخواه شروع روی رأس B، گزینه‌های A ،C و E را در اختیار داریم. وزن‌های متناظر این یال‌ها به ترتیب برابر با 0، 0 و 5 است. از این رو کمینه آن یعنی 2 را انتخاب می‌کنیم. از آنجا که در این مثال دو یال را وزن 2 داریم، می‌توانیم هر کدام از آن‌ها را انتخاب کنیم. فعلاً این که کدام را انتخاب می‌کنیم اهمیتی ندارد. برای مثال فرض کنید رأس A را انتخاب می‌کنیم:
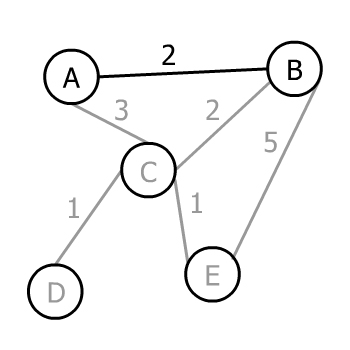
اکنون درختی با دو رأس A و B داریم می‌توانیم هر کدام از یال‌های A یا B را که هنوز اضافه نشده به یک رأس اضافه نشده انتخاب کنیم. بنابراین می‌توانیم AC ،BC یا BE را انتخاب کنیم. الگوریتم پریم مقدار مینیمم را انتخاب می‌کند که برابر با 2 یا BC است.
اکنون درختی با سه رأس و سه یال ممکن برای حرکت به جلو به صورت CD ،CE یا BE داریم. AC در این لیست نیست، زیرا رأس جدیدی به درخت اضافه نمی‌کند. کمینه وزن در میان این سه یال برابر با 1 است. با این حال دو یال وجود دارند که هر دو وزن 1 دارند. در نتیجه الگوریتم پریم یکی از آن‌ها را انتخاب می‌کند. این بار نیز مهم نیست کدام را انتخاب می‌کنیم:
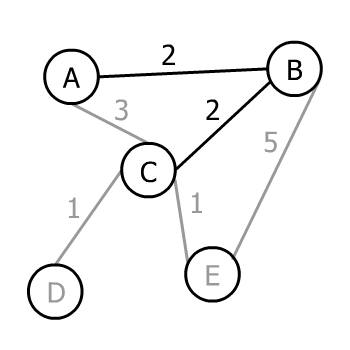
اینک تنها یک رأس باقیمانده است، بنابراین می‌توانیم از CE و BE انتخاب کنیم. کمینه وزن که درخت ما را وصل کند برابر با 1 است و آن را انتخاب می‌کنیم.
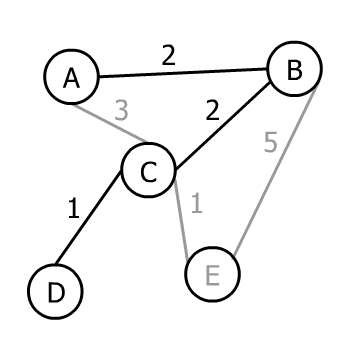
از آنجا که همه رئوس گراف ورودی هم اینک در درخت خروجی حاضر هستند، الگوریتم پریم پایان می‌یابد. بدین ترتیب این درخت یک MST از گراف ورودی است.
روش دیگری که برای پیدا کردن « مقدار کمینه درخت پوشا» (Minimum Spanning Tree | MST) در گراف‌های همبند وزن‌دار غیر جهت‌دار به‌کار می‌رود استفاده از الگورتیم کروسکال است.
پیاده‌سازی
رأس‌ها و یال‌ها گراف را می‌سازند، از این رو باید ساحتمان داده‌ای برای ذخیره‌سازی این عناصر داشته باشیم. ابتدا یک کلاس Edge می‌سازیم:
1public class Edge {
2
3 private int weight;
4 private boolean isIncluded = false;
5
6}هر Edge باید یک Weight داشته باشد، زیرا الگوریتم پریم روی گراف‌های وزن‌دار کار می‌کند. isIncluded نشان می‌دهد که آیا یال مورد نظر در درخت کمینه‌ی پوشا حضور دارد یا نه. اینک کلاس Vertex را اضافه می‌کنیم:
1public class Vertex {
2
3 private String label = null;
4 private Map<Vertex, Edge> edges = new HashMap<>();
5 private boolean isVisited = false;
6
7}هر Vertex می‌تواند یک Label داشته باشد، ما از یک map به نام edges برای ذخیره اتصال‌ها میان رئوس استفاده می‌کنیم. در نهایت isVisited نشان می‌دهد که آیا رأس مورد نظر تاکنون از سوی الگوریتم پریم بازدید شده است یا نه. کلاس Prim ما جایی است که منطق را پیاده‌سازی می‌کنیم:
1public class Prim {
2
3 private List<Vertex> graph;
4
5}لیستی از رئوس برای ذخیره‌سازی کل گراف کافی است، زیرا درون هر Vertex یک Map<Vertex, Edge> داریم که همه اتصال‌ها را شناسایی می‌کند. درون Prim متد ()run را ایجاد می‌کنیم:
1public void run() {
2 if (graph.size() > 0) {
3 graph.get(0).setVisited(true);
4 }
5 while (isDisconnected()) {
6 Edge nextMinimum = new Edge(Integer.MAX_VALUE);
7 Vertex nextVertex = graph.get(0);
8 for (Vertex vertex : graph) {
9 if (vertex.isVisited()) {
10 Pair<Vertex, Edge> candidate = vertex.nextMinimum();
11 if (candidate.getValue().getWeight() < nextMinimum.getWeight()) {
12 nextMinimum = candidate.getValue();
13 nextVertex = candidate.getKey();
14 }
15 }
16 }
17 nextMinimum.setIncluded(true);
18 nextVertex.setVisited(true);
19 }
20}کار خود را با تعیین عنصر نخست گراف List<Vertex> به صورت بازدید شده آغاز می‌کنیم. عنصر اول بسته به ترتیبی که به لیست اضافه شده است، می‌تواند هر یک از رئوس باشد. ()isDisconnected در صورتی مقدار true بازگشت می‌دهد که vertex تاکنون بازدید نشده باشد:
1private boolean isDisconnected() {
2 for (Vertex vertex : graph) {
3 if (!vertex.isVisited()) {
4 return true;
5 }
6 }
7 return false;
8}با این که درخت پوشای کمینه به صورت ()isDisconnected است، روی رئوس قبلاً بازدید شده حلقه‌ای تعریف می‌کنیم و آن Edge را که دارای کمترین وزن است به عنوان رأس بعدی برای nextVertex انتخاب می‌کنیم:
1public Pair<Vertex, Edge> nextMinimum() {
2 Edge nextMinimum = new Edge(Integer.MAX_VALUE);
3 Vertex nextVertex = this;
4 Iterator<Map.Entry<Vertex,Edge>> it = edges.entrySet()
5 .iterator();
6 while (it.hasNext()) {
7 Map.Entry<Vertex,Edge> pair = it.next();
8 if (!pair.getKey().isVisited()) {
9 if (!pair.getValue().isIncluded()) {
10 if (pair.getValue().getWeight() < nextMinimum.getWeight()) {
11 nextMinimum = pair.getValue();
12 nextVertex = pair.getKey();
13 }
14 }
15 }
16 }
17 return new Pair<>(nextVertex, nextMinimum);
18}بدین ترتیب کمینه همه رئوس بالقوه را در حلقه اصلی می‌یابیم و در nextVertex ذخیره می‌کنیم. سپس nextVertex را به صورت بازدید شده علامت‌گذاری می‌کنیم. این حلقه تا زمانی که همه رئوس بازدید شوند ادامه می‌یابد و در نهایت هر یال با مقدار isIncluded به صورت true در MST حضور دارد.
توجه کنید که چون ()nextMinimum روی یال‌ها می‌چرخد، پیچیدگی زمانی این پیاده‌سازی برابر با O(v^2) است. اگر یال‌ها را در یک صف اولویت (که بر مبنای وزن مرتب‌سازی شده) ذخیره کنیم، این الگوریتم در زمان O(E log V) اجرا می‌شود.
تست کردن
اینک که کد الگوریتم درخت پوشای کمینه را پیاده‌سازی کردیم، نوبت آن رسیده است که با یک مثال واقعی تست کنیم ابتدا گراف زیر را می‌سازیم:
1public static List<Vertex> createGraph() {
2 List<Vertex> graph = new ArrayList<>();
3 Vertex a = new Vertex("A");
4 ...
5 Vertex e = new Vertex("E");
6 Edge ab = new Edge(2);
7 a.addEdge(b, ab);
8 b.addEdge(a, ab);
9 ...
10 Edge ce = new Edge(1);
11 c.addEdge(e, ce);
12 e.addEdge(c, ce);
13 graph.add(a);
14 ...
15 graph.add(e);
16 return graph;
17}سازنده کلاس Prim آن را می‌گیرد و درون کلاس ذخیره می‌کند. می‌توانیم گراف را با متد ()originalGraphToString ذخیره کنیم:
1Prim prim = new Prim(createGraph());
2System.out.println(prim.originalGraphToString());اکنون مثال ما یک خروجی به صورت زیر دارد:
1A --- 2 --- B
2A --- 3 --- C
3B --- 5 --- E
4B --- 2 --- C
5C --- 1 --- E
6C --- 1 --- Dاکنون می‌توانیم الگوریتم پریم را اجرا کرده و نتیجه MST را با متد ()minimumSpanningTreeToString چاپ کنیم:
1prim.run();
2prim.resetPrintHistory();
3System.out.println(prim.minimumSpanningTreeToString());در نهایت MST را چاپ می‌کنیم:
1A --- 2 --- B
2B --- 2 --- C
3C --- 1 --- E
4C --- 1 --- Dسخن پایانی
در این مقاله با طرز کار الگوریتم پریم و تشکیل یک درخت پوشای کمینه از یک گراف آشنا شدیم. همه کدهای مطرح شده در این مقاله را می‌توانید در این رپیوی گیت‌هاب (+) ملاحظه کنید.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد می‌شوند:
- مجموعه آموزش برنامهنویسی جاوا
- مجموعه آموزشهای برنامهنویسی
- آموزش نصب اندروید استودیو (Android Studio) (رایگان)
- زبان برنامه نویسی جاوا (Java) — از صفر تا صد
- چگونه از ArrayList در جاوا استفاده کنیم؟
==
