نحوه انجام عملیات ریاضی در کامپیوترها — به زبان ساده

شاید شما نیز تاکنون در مورد نحوه انجام عملیات ریاضی در کامپیوترها که در سطح پایین صورت می‌پذیرد کنجکاو شده باشید. همه ما کمابیش می‌دانیم که رایانه‌ها عملیات ریاضیاتی را به روشی متفاوت از انسان‌ها اجرا می‌کنند، زیرا رایانه‌ها به روش دودویی (Binary) عمل می‌کنند. در این نوشته به بررسی عملیات ریاضیاتی در رایانه‌ها از طریق معرفی عملگرهای منطقی می‌پردازیم. شما می‌توانید در دنیای فیزیکی به جای عملگرهای منطقی گیت‌های متناظرشان را قرار دهید.

دقت کنید که برای درک نیمه دوم این راهنما باید با جبر بولی آشنا باشید و این موضوع در راهنمای حاضر معرفی نشده است. در این خصوص، می‌توانید این مطلب را مطالعه کنید.

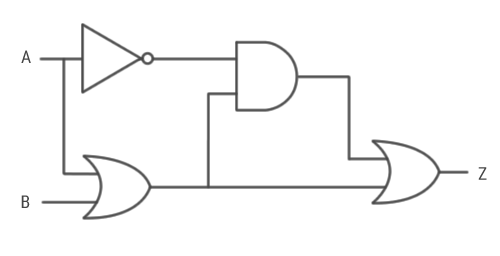
چرا باید از دودویی استفاده کنیم؟

این مقاله را با یک سؤال ساده شروع می‌کنیم. ما چرا به روش کنونی می‌شماریم؟ چرا از اعداد 1، 2، 3، 4، 5، 6،7، 8، 9 و 10 برای شمارش استفاده می‌کنیم؟ هر عددی که پس از این‌ها بیاید صرفاً با تکثیر رقم‌ها یا جابجایی آن‌ها بیان می‌شود.

فیلم آموزش مبانی منطق و نظریه مجموعه ها در فرادرس

کلیک کنید

برای نمونه چرا ما برای شمارش فقط از ارقام 1، 2، 3، 4، 5، 6، 7، و 10 استفاده نمی‌کنیم؟ شاید در ابتدا این مسئله یک انتخاب دلخواه به نظر برسد، اما اگر عمیق‌تر شویم یک دلیل احتمالی شاید این باشد که تعداد انگشت‌های دست انسان 10 تا است.

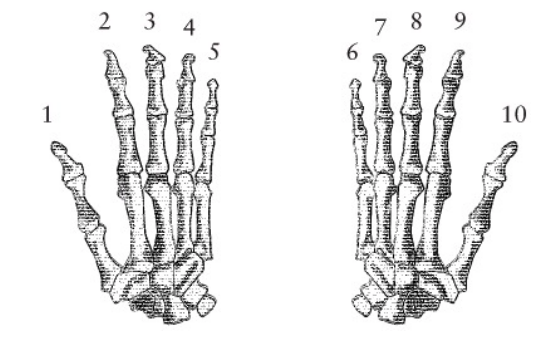
ما در هر دست خود 10 انگشت داریم و از این رو سیستم اعداد که استفاده می‌کنیم هم بر مبنای 10 رقم است. متأسفانه مدارهای الکترونیکی از این موهبت خدادادی برخوردار نیستند. این مدارها در هر زمان تنها یکی از دو حالت را می‌توانند نمایش دهند که به صورت حضور یا عدم حضور جریان در سیم‌ها نمایش می‌یابد. بنابراین ما در مدار الکتریکی با استفاده از 1 و 10 می‌شماریم.

اکنون یکی از سؤالات بدیهی این است که چرا 1 و 10؟ چرا 1 و 2 نباشد؟ برای پاسخ به این سؤال باید کمی توضیح دهیم.

اهمیت صفر

برای درک اهمیت صفر باید دو سیستم متفاوت شمارش یعنی روش مدرن هندو-عربی و شمارش با استفاده از اعداد رومی را با هم مقایسه کنیم.

• سیستم هندوعربی: 10، 9، 8، 7، 6، 5، 4، 3، 2، 1
• سیستم رومی: I، II، III، IV، V، VI، VII، VIII، IX، X

تفاوت مهم بین این دو سیستم در عدد آخر است. در سیستم رومی نماد خاصی برای عدد 10 وجود دارد. برای درک این تفاوت یک مثال ساده را بررسی می‌کنیم. در خط زیر روش نوشتن عدد 205 را در سیستم اعداد رومی مشاهده می‌کنید:

CCV

با این وجود، همین عدد در سیستم هندو-عربی به روش زیر نوشته می‌شود:

205 = 2 * 100 + 0 * 10 + 5 * 1

هیچ ارتباط بدیهی بین عدد و سیستم اعداد رومی وجود ندارد؛ در حالی که بین عدد 205 و موقعیت ارقام مختلف یک همبستگی مشخص وجود دارد.

این اهمیت صفر را مشخص می‌کند. صفر امکان تعریف جایگاه برای ارقام در سیستم اعداد را فراهم ساخته است.

اگر هنوز قانع نشده‌اید، به تفاوت‌های نمایشی بین سیستم اعداد رومی و هندو-عربی در ادامه توجه کنید:

Hindu-Arabic    Roman
100          C
1000         M

شمارش در سیستم دودویی

در ادامه روش شمارش در سیستم دودویی یا باینری را بررسی می‌کنیم. در این سیستم اعداد به ترتیب به صورت 00، 10، 01، 11 است. هر کدام از این ارقام یک بیت نامیده می‌شوند. به این اعداد، اعداد دودویی 2-بیتی گفته می‌شود.

مفهوم 2-بیت را نباید با دودویی اشتباه بگیرید. منظور از دودویی این است که ما برای هر موقعیت از ارقام 0 یا 1 استفاده می‌کنیم. تعداد بیت‌ها نشان‌دهنده تعداد ارقام هر عدد است. اینک باید مواردی را در مورد اجرای عملیات جبر بولی روی هر یک از اعداد دودویی یاد بگیریم. اگر می‌خواهید در مورد جبر بولی بیشتر بدانید، بهتر است ابتدا مقاله «منطق ترکیبی به زبان ساده» را مطالعه کنید. در ادامه تصویری از نتیجه سه عملیات متفاوت جبر بولی را مشاهده می‌کنید. این عملیات به نام گیت‌های منطقی نیز نامیده می‌شوند:

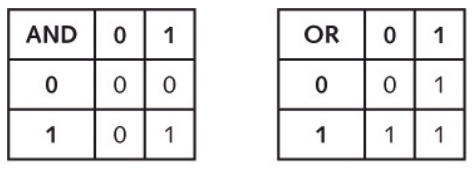
می‌توان همه گیت‌های منطقی فوق را با استفاده از مدارها و قطعات الکتریکی ساخت. در این نوشته قصد نداریم به شیوه ساخت این مدارها بپردازیم، چون خارج از حیطه این مقاله است. در لینکی که در بخش قبل ارائه کردیم می‌توانید در این مورد بیشتر مطالعه کنید.

آنچه فعلاً باید بدانیم این است که چگونه می‌توانیم هر یک از این گیت‌های منطقی را در کد نمایش دهیم. برای نمونه در جاوا اسکریپت از عملگرهای زیر استفاده می‌کنیم:

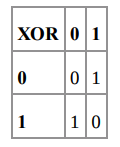
AND &
OR |
XOR ^

این عملگرها به نام عملگرهای سطح بیتی نیز نامیده می‌شوند و در ادامه در مورد آن‌ها بیشتر توضیح می‌دهیم. عملگرهای سطح بیتی را می‌توان مشابهی برای گیت‌های منطقی برشمرد. در این خصوص می‌توانید در مقاله «منطق شرطی (Conditional Logic) در جاوا اسکریپت» بیشتر بخوانید.

ساخت یک ماشین جمع کننده دودویی

بدین ترتیب ما تا به اینجا قواعد مقدماتی مورد نیاز برای جبر بولی را داریم. اینک چگونه می‌توانیم دو عدد دودویی را با هم جمع بکنیم؟ به جدول زیر توجه کنید:

+ 0 1
0 00 01
1 01 10

ما نتیجه را با استفاده از 2 بیت ارائه کرده‌ایم. بیت راست، بیت مجموع است و بیت سمت چپ به نام بیت انتقالی (carry bit) نامیده می‌شود.

اگر جدول را به دو جدول مجزا، یکی برای نمایش بیت مجموع و دیگری برای نمایش بیت انتقالی تقسیم کنیم به شکل زیر درمی‌آید:

ما اینک همه چیزهایی که برای عمل جمع در سیستم دودویی مورد نیاز است را می‌دانیم. در ادامه باید روشی برای نمایش دو جدول فوق برحسب کد پیدا کنیم.

ترکیب مدارها و کد

اینک آنچه را که تا اینجا آموخته‌ایم یادآوری می‌کنیم:

فیلم آموزش جاوا اسکریپت JavaScript در فرادرس

کلیک کنید

1. ما سه گیت منطقی متفاوت و عملگرهای متناظرشان را در جاوا اسکریپت می‌شناسیم.
2. ما چگونگی افزودن دو عدد دودویی به صورت دستی با استفاده از جدول‌های جمع و انتقالی که قبلاً اشاره کردیم را می‌دانیم.

ما باید روشی برای بیان 2 جدول در 1 جدول پیدا کنیم. بدین ترتیب دو عدد دودویی را با استفاده از عملگرهای بیتی متفاوت جمع می‌کنیم. در ادامه جدول‌های جمع و انتقالی را به طور مجزا بررسی می‌کنیم. ابتدا جدول جمع را در نظر بگیرید.

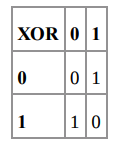
اگر به ابتدای این مقاله بازگردید، می‌بینید که سه جدول گیت منطقی یعنی AND ،OR و XOR را داریم. اگر مقادیر هر سلول جدول جمع و جدول XOR را مقایسه کنیم، درمی‌یابیم که مطابقت دقیقی وجود دارد.

بنابراین اگر دو عدد دودویی به صورت 0 و 1، وجود داشته باشد، با انجام کارهای زیر بیت مجموع به دست می‌آید. شما می‌توانید وضعیت را در پنجره dev tools در مرورگر امتحان کنید.

1let a = 0
2let b = 1
3let result = a ^ b
4// result = 1

سپس بیت انتقالی را در نظر بگیرید. همین کار را انجام دهید و با مراجعه به بخش‌های قبلی، سه جدول منطقی را که داریم در نظر بگیرید و آن‌ها را با جدول انتقالی مقایسه کنید. درخواهید یافت که جدول‌های انتقالی مطابقت دقیق دارند. این وضعیت را در کد به صورت زیر بیان می‌کنیم:

1let a = 0
2let b = 1
3let result = a & b
4// result = 0

بنابراین می‌توانیم دو عدد 1 بیتی را با هم جمع کنیم و بیت جمع و بیت انتقالی را با استفاده از ترکیبی از یک گیت AND و گیت XOR به دست آوریم. این گیت را نیم‌جمع‌کننده می‌نامیم.

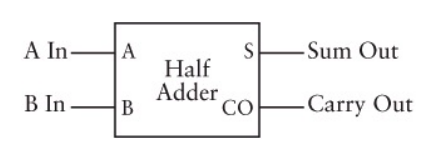
گیت نیم‌جمع‌کننده را به صورت زیر کدنویسی می‌کنیم. در کد زیر اعداد 1010 و 0101 را با هم جمع می‌کنیم. در مبنای 10 این دو عدد به ترتیب 10 و 5 نامیده می‌شوند.

1 0 1 0
0 1 0 1
-------
1 1 1 1

بنابراین می‌دانیم که این کار را چگونه به صورت دستی انجام دهیم و از این رو هر ستون اساساً عملیات یکسانی به صورت یعنی جمع 1 و 0 است. می‌دانیم که نتیجه این جمع 1 است. کد آن به صورت زیر است:

1function halfAdder(a, b) {
2  return { sum: a ^ b, carry: a & b }
3}
4
5function convert2Binary(num) {
6  return ('00000000' + num.toString(2)).substr(-8);
7}
8
9function performReduction(acc, curr, index) {
10  const result = halfAdder(curr, binSplit[index])
11  acc.push(result.sum)
12  return acc
13}
14
15function add(a, b) {
16  const bin1 = convert2Binary(a)
17  const bin2 = convert2Binary(b)
18  binSplit = bin2.split('')
19  return bin1.split('').reduceRight(performReduction, []).reverse().join('')
20}
21
22const result = add(5, 10)
23console.log(result)

اگر کد فوق را اجرا کنیم، باید نتیجه 15 را ببینیم که همان چیزی است که انتظار داریم.

با این وجود، یک موقعیتی وجود دارد که هنوز کد آن را ننوشته‌ایم. اگر به عقب بازگردید و به دو عدد دودویی که جمع کردیم نگاه کنید، متوجه خواهید شد که هرگز در هیچ کدام از جمع‌ها، انتقال بیت صورت نگرفته است. اگر لازم باشد که دو عدد زیر را با هم جمع کنیم چه اتفاق می‌افتد؟

0 0 1 1
1 0 1 1
-------
1 1 1 0

دقت کنید که کد فوق نمی‌تواند پاسخ صحیح را بدهد، زیرا ما هرگز انتقال از یک ستون به ستون بعد را انجام نداده‌ایم. در واقع مفهوم ما از نیم‌جمع‌کننده نمی‌تواند این کار را انجام دهد، زیرا نیم‌جمع‌کننده تنها مسئول دو بیت ورودی A و B است. ما به چیزی نیاز داریم که سه بیت ورودی را مدیریت کند.

مدار تمام‌ جمع‌ کننده

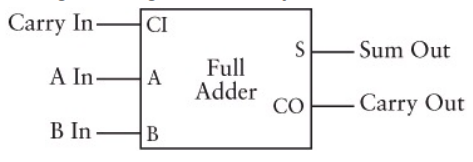
مدار تمام‌جمع‌کننده در پس‌زمینه تنها ترکیبی از دو نیم‌جمع‌کننده است که با گیت OR به صورت سری به هم اضافه شده‌اند. برای نمایش تمام‌جمع‌کننده برحسب برنامه‌نویسی، قصد داریم زمانی را صرف بررسی کامل آن بکنیم.

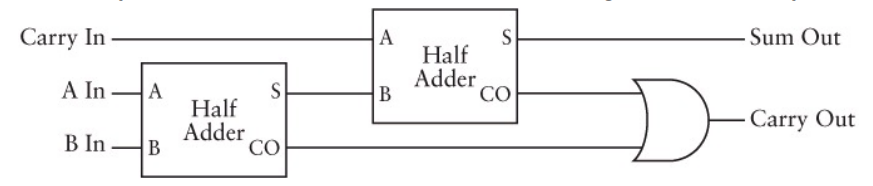
شاید توضیح چگونگی کارکرد این مدار کمی دشوار باشد. ما روش کارکرد این مدار را با استفاده از ستون دوم از راست جمع که اینک روی آن کار می‌کنیم توضیح می‌دهیم و با این توضیح، درک آن کمی آسان‌تر می‌شود.

تصویر فوق نسخه حاشیه‌نویسی شده‌ای از ستون دوم از راست برای جمع زیر به دست می‌دهد:

0 0 1 1
1 0 1 1
-------
1 1 1 0

• دو ورودی به نیم‌جمع‌کننده در مدار، دو مقداری در ستون‌ها هستند که هر دو 1 هستند.
• ورودی‌ها به دومین نیم‌جمع‌کننده در مدار مجموع نیم‌جمع‌کننده قبلی هستند و از ستون چپ انتقال می‌یابند.
• انتقالی از ستون فعلی و انتقالی از ستون سمت راست هر دو به گیت OR بعدی وارد می‌شوند. نتیجه این محاسبه OR انتقالی از این ستون به ستون چپ است.

ما چرا آن گیت OR را در انتها داریم؟ چرا نیم‌جمع‌کننده دیگری در آنجا نداریم؟ البته این کار ممکن است اما گیت OR بسیار ساده‌تر است. دلیل این که گیت OR برای نیازهای ما کافی است این است که هیچ مجموعه ورودی دیگری برای دو نیم‌جمع‌کننده اول وجود ندارد که دو 1 به عنوان ورودی‌های گیت OR ارائه کند. شما می‌توانید با بررسی وضعیت‌های مختلف درستی این گزاره را خودتان امتحان کید.

اینک تمام‌جمع‌کننده را در کد زیر نمایش می‌دهیم:

1/**
2 * 
3 * @param {String} a 
4 * @param {String} b 
5 * @param {String} carryIn 
6 */
7function fullAdder(a, b, carryIn) {
8  const [halfSum1, halfCarry1] = halfAdder(a, b);
9  const [halfSum2, halfCarry2] = halfAdder(carryIn, halfSum1)
10  return { sum: halfSum2, carryOut: halfCarry1 | halfCarry2 }
11}
12
13/**
14 * 
15 * @param {String} a 
16 * @param {String} b 
17 */
18function halfAdder(a, b) {
19  return [a ^ b, a & b]
20}
21
22/**
23 * 
24 * @param {Number} num
25 * @param {Number} padding
26 * @return {String} 
27 */
28function convert2Binary(num, padding) {
29  return ('00000000' + num.toString(2)).substr(-padding);
30}
31
32/**
33 * 
34 * @param {String} bin
35 * @returns {Number} 
36 */
37function convert2Decimal(bin) {
38  return parseInt(bin, 2)
39}
40
41/**
42 * 
43 * @param {String} num1 
44 * @param {String} num2 
45 */
46function addReduction(num1, num2) {
47  let binSplit = num2.split('')
48  let carryIn = 0
49  let result = num1.split('').reduceRight(function performReduction(acc, curr, index) {
50    const result = fullAdder(curr, binSplit[index], carryIn)
51    carryIn = result.carryOut
52    acc.push(result.sum)
53    return acc
54  }, [])
55  carryIn === 1 ? result.push(carryIn) : null
56  return result.reverse().join('')
57}
58
59/**
60 * 
61 * @param {String} num1 
62 * @param {String} num2 
63 * @param {Number} operationBit 0 to perform addition, 1 to perform subtraction
64 * @returns {String}
65 */
66function binaryAdder(num1, num2) {
67  return addReduction(num1, num2)
68}
69
70/**
71 * 
72 * @param {String} num1 
73 * @param {String} num2
74 * @returns {String}
75 */
76function add(num1, num2) {
77  const bin1 = convert2Binary(num1, 8)
78  const bin2 = convert2Binary(num2, 8)
79  const result = binaryAdder(bin1, bin2)
80  return convert2Decimal(result)
81}
82
83const result = add(3, 11)

احتمالاً متوجه چند تفاوت در روش سازماندهی کد برای نیم‌جمع‌کننده و تمام‌جمع‌کننده شده‌اید و تفاوت عملکردی اصلی متغیری است که به طور مداوم با بیت انتقالی از ستون قبلی بازنویسی می‌شود.

ضمناً در انتهای عملیات، carryIn === 1 را برسی می‌کنیم تا مطمئن شویم که انتقالی از ستون سمت چپ را از دست نداده‌ایم. همچنین یک تابع کمکی کوچک به نام convert2Decimal اضافه می‌کنیم تا بتوانیم نتیجه را در مبنای 10 ببینیم.

اگر می‌خواهید در مورد این وضعیت به صورت فیزیکی تصوری داشته باشید، در تصویر زیر هر آن چه را تاکنون مطرح کردیم، جمع‌بندی نموده‌ایم.

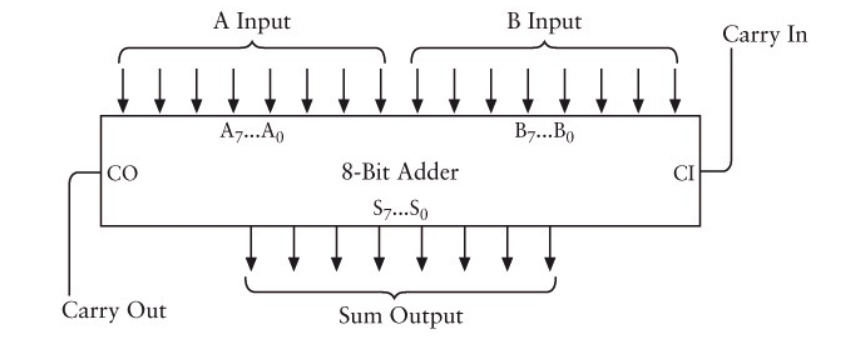
محاسبه هر ستون نیازمند یک تمام‌جمع‌کننده است. از این رو جمع کننده 8 بیتی ما از 8 آدرس کامل تشکیل یافته است. بیت‌های نقلی خروجی از هر یک از این جمع‌کننده‌ها به عنوان بیت نقلی ورودی برای جمع کننده بعدی استفاده می‌شوند.

مجموع بیت‌ها از هر ستون انتقال می‌یابند و با هم تجمیع می‌شوند تا یک خروجی جمع 8 بیتی تولید کنند.

ساخت یک ماشین تفریق باینری

اینک که با روش جمع دودویی در کدهای نرم‌افزاری آشنا شدیم، نوبت آن رسیده است که تفریق دودویی را بررسی کنیم. ما تفریق را به صورت تفریقی برای یک جمع کننده 8 بیتی که در بخش قبلی ساختیم تعریف می‌کنیم.

فیلم آموزش ریاضی مهندسی در فرادرس

کلیک کنید

ماشین تفریق باینری که در این راهنما می‌سازیم دو محدودیت دارد:

1. تنها می‌تواند اعداد 8 بیتی را مدیریت کند.
2. تنها اعدادی با نتیجه مثبت را از هم تفریق می‌کند.

این محدودیت‌ها جهت کاهش پیچیدگی مسئله با مقاصد آموزشی اعمال شده‌اند. ابتدا به روش معمول تفریق دستی توجه کنید:

 253      Minuend
-176      Subtrahend
----
 077      Result

با توجه به مقادیر فوق می‌بینیم که اصطلاح‌های خاصی بدین منظور وجود دارد. برای اجرای تفریق فوق باید برخی اعداد را از چپ قرض بگیریم. انجام این کار روی اعداد دودویی کمی پیچیده است. در ادامه یک ترفند ریاضیاتی که در کد استفاده می‌شود را ارائه کرده‌ایم.

   253 - 176
=  253 - 176 + 1000 - 1000           // add and subtract 1000
=  253 - 176 + 999 + 1 - 1000        // split 1000 into 999 + 1
=  253 + (999 - 176) + 1 - 1000      // rearrange the numbers
=  77

زیبایی این ترفند آن است که دیگر به قرض کردن عدد در هیچ عملیاتی نیاز نداریم. مهم‌ترین بخش مراحل فوق قسمت زیر است:

999 — 176

نتیجه این تفریق مکمل 9 برای عدد 176 نامیده می‌شود.

ما در سیستم دودویی به مکمل 1 نیاز داریم که به صورت زیر نمایش می‌یابد (در این عملیات بازنمایی دودویی از 255 استفاده می‌شود که بزرگ‌ترین عدد ممکن با 8 بیت است):

  255 - 176
= 11111111 - 10110000
= 01001111

اگر به دقت به عدد دودویی در سمت راست تفریق و نتیجه تفریق نگاه کنید، می‌بینید که نتیجه دقیقاً متضاد سمت راست است، یعنی هر کجا 1 بوده 0 شده و هر کجا 0 بوده 1 شده است.

یک روش سریع برای شبیه‌سازی این وضعیت در جاوا اسکریپت استفاده از عملگر ~ است. اما مشکلی در بازنمایی جاوا اسکریپت از اعداد دودویی منفی و مثبت وجود دارد.

جاوا اسکریپت همه اعداد را تنها به صورت اعداد اعشاری نشان می‌دهد. البته جاوا اسکریپت در سازوکار درونی خود این اعداد را در موارد مقتضی به اعداد صحیح تبدیل می‌کند و پس از انجام محاسبات مورد نیاز دوباره به حالت اعشاری بازمی‌گرداند. جاوا اسکریپت از دو نسخه علامت‌دار و بی‌علامت برای بازنمایی درونی اعداد استفاده می‌کند.

اگر خواهیم از عملگر ~ استفاده کنیم، باید تنها از اعداد صحیح بی‌علامت استفاده کنیم.

از آنجا که جاوا اسکریپت یک زبان با نوع‌بندی سست (loosely typed) است، می‌توانیم اعداد صحیح علامت‌دار را به اعداد صحیح بی‌علامت تبدیل می‌کنیم و سپس آن‌ها را مورد استفاده قرار دهیم. عملگری که استفاده می‌کنیم عملگر >>> است.

به تابع convert2Binary خود که قبلاً استفاده کردیم، کدی به صورت زیر اضافه می‌کنیم:

function convert2Binary(num, padding) {
  return ('00000000' + (num >>> 0).toString(2)).substr(-padding)
}

به تابع فوق دو مورد اضافه می‌کنیم:

1. یک پارامتر اضافی به نام padding اضافه می‌کنیم. بدین ترتیب می‌توانیم تعداد رقم‌هایی که هنگام تبدیل به دودویی استفاده می‌شوند را کنترل می‌کنیم. با استفاده از این بخش می‌توانیم به طور موقت عدد 256 را به عنوان یک مرحله میانی مدیریت کنیم.
2. پارامتر num را پیش از تبدیل شدن به دودویی به دست می‌آوریم.

در ادامه عملگرهایی که قصد داریم بار دیگر اجرا کنیم را بررسی می‌کنیم.

1253 + (999 - 176) + 1 - 1000
2
3      |    a    |
4|      b         |
5|             c      |
6|               d           |

خطوط عمودی نشان‌دهنده کران‌های هر یک از مراحل هستند. برای نمونه مرحله a تنها روی اعداد درون پرانتزها اجرا می‌شود و همین طور تا آخر. این ترتیب عملیات در کد نیز رعایت شده است. در ادامه کد تابع تفریق را می‌بینید:

1/**
2 * 
3 * @param {String} num1 The minuend
4 * @param {String} num2 The subtrahend
5 */
6function subtract(num1, num2) {
7  if (num1 > 255 || num2 > 255) {
8    throw new Error('Sorry, can only handle 8-bit numbers')
9  }
10  const bin1 = convert2Binary(num1, 8) //minuend
11  const bin2flip = convert2Binary(~num2, 8) // 1's complement of subtrahend
12  const result1 = binaryAdder(bin1, bin2flip)
13  const result2 = binaryAdder(result1, convert2Binary(1, 8))
14  const result3 = binaryAdder(result2, convert2Binary(256, 9), 1)
15  return convert2Decimal(result3)
16}

در ابتدای تابع یک رویه مدیریت خطای بسیار ساده وجود دارد. ضمناً وقتی عدد 256 را به تابع convert2Binary ارسال می‌کنیم یک فاصله‌گذاری 9 نیز می‌فرستیم. دلیل این مسئله آن است که 255 بزرگ‌ترین عددی است که می‌توان با 8 بیت نشان داد و از این رو در این مورد به 9 بیت نیاز داریم.

یک مرحله دیگر هم وجود دارد که باید ارائه کنیم. مرحله d الزام می‌کند که رقم نقلی خروجی از تفریق را داشته باشیم. چگونه می‌توانیم این رقم نقلی را از تفریق خارج کنیم؟

اگر مجدداً به گیت‌های منطقی خود فکر کنیم، متوجه می‌شویم کد منطقی یک شبیه‌سازی از عملیات تفریق است.

گیت XOR دقیقاً آن چیزی که نیاز داریم را در اختیار ما قرار می‌دهد. از آنجا که تنها تفریقی که انجام می‌دهیم، رقم خروجی بین 256 (با نمایش دودویی 100000000) و عددی کمتر از 256 است، از این رو هرگز نباید نگران قرض گرفتن عددها باشیم. در ادامه کد آنچه که convert2Binary می‌نامیم را می‌بینید:

1/**
2 * 
3 * @param {String} a 
4 * @param {String} b 
5 */
6function fullSubtractor(a, b) {
7  return a ^ b
8}

همچنین می‌خواهیم تابع binaryAdder را که در بخش قبلی توسعه دادیم ببینیم. از آنجا که امکان اجرای جمع یا تفریق را با استفاده از جمع کننده 8 بیتی یکسانی داریم، باید بین زمان‌هایی که می‌خواهیم جمع یا تفریق کنیم تمایزی قائل شویم. ما از یک عدد به عنوان پارامتر به این منظور استفاده می‌کنیم. بدین ترتیب 0 به معنی جمع و 1 به معنی تفریق خواهد بود.

1/**
2 * 
3 * @param {String} num1 
4 * @param {String} num2 
5 * @param {Number} operationBit 0 to perform addition, 1 to perform subtraction
6 * @returns {String}
7 */
8function binaryAdder(num1, num2, operationBit = 0) {
9  if (num1.length !== num2.length) {
10    let l = num1.length > num2.length ? num1.length : num2.length
11    num1 = convert2Binary(convert2Decimal(num1), l)
12    num2 = convert2Binary(convert2Decimal(num2), l)
13  }
14  return operationBit ? subReduction(num1, num2) : addReduction(num1, num2)
15}

در نهایت کد کامل ما به صورت زیر است:

1/**
2 * 
3 * @param {String} a 
4 * @param {String} b 
5 * @param {String} carryIn 
6 */
7function fullAdder(a, b, carryIn) {
8  const [halfSum1, halfCarry1] = halfAdder(a, b);
9  const [halfSum2, halfCarry2] = halfAdder(carryIn, halfSum1)
10  return { sum: halfSum2, carryOut: halfCarry1 | halfCarry2 }
11}
12
13/**
14 * 
15 * @param {String} a 
16 * @param {String} b 
17 */
18function halfAdder(a, b) {
19  return [a ^ b, a & b]
20}
21
22/**
23 * 
24 * @param {String} a 
25 * @param {String} b 
26 */
27function fullSubtractor(a, b) {
28  return a ^ b
29}
30
31/**
32 * 
33 * @param {String} bin
34 * @returns {Number} 
35 */
36function convert2Decimal(bin) {
37  return parseInt(bin, 2)
38}
39
40/**
41 * 
42 * @param {Number} num
43 * @param {Number} padding
44 * @return {String} 
45 */
46function convert2Binary(num, padding) {
47  return ('00000000' + (num >>> 0).toString(2)).substr(-padding);
48}
49
50/**
51 * 
52 * @param {String} num1 
53 * @param {String} num2 
54 */
55function subReduction(num1, num2) {
56  let binSplit = num2.split('')
57  let result = num1.split('').reduceRight(function performReduction(acc, curr, index) {
58    let result = fullSubtractor(curr, binSplit[index])
59    acc.push(result)
60    return acc
61  }, [])
62  return result.reverse().join('')
63}
64
65/**
66 * 
67 * @param {String} num1 
68 * @param {String} num2 
69 */
70function addReduction(num1, num2) {
71  let binSplit = num2.split('')
72  let carryIn = 0
73  let result = num1.split('').reduceRight(function performReduction(acc, curr, index) {
74    const result = fullAdder(curr, binSplit[index], carryIn)
75    carryIn = result.carryOut
76    acc.push(result.sum)
77    return acc
78  }, [])
79  carryIn === 1 ? result.push(carryIn) : null
80  return result.reverse().join('')
81}
82
83/**
84 * 
85 * @param {String} num1 
86 * @param {String} num2 
87 * @param {Number} operationBit 0 to perform addition, 1 to perform subtraction
88 * @returns {String}
89 */
90function binaryAdder(num1, num2, operationBit = 0) {
91  if (num1.length !== num2.length) {
92    let l = num1.length > num2.length ? num1.length : num2.length
93    num1 = convert2Binary(convert2Decimal(num1), l)
94    num2 = convert2Binary(convert2Decimal(num2), l)
95  }
96  return operationBit ? subReduction(num1, num2) : addReduction(num1, num2)
97}
98
99/**
100 * 
101 * @param {String} num1 
102 * @param {String} num2
103 * @returns {String}
104 */
105function add(num1, num2) {
106  const bin1 = convert2Binary(num1, 8)
107  const bin2 = convert2Binary(num2, 8)
108  const result = binaryAdder(bin1, bin2)
109  return convert2Decimal(result)
110}
111
112/**
113 * 
114 * @param {String} num1 The minuend
115 * @param {String} num2 The subtrahend
116 */
117function subtract(num1, num2) {
118  if (num1 > 255 || num2 > 255) {
119    throw new Error('Sorry, can only handle 8-bit numbers')
120  }
121  const bin1 = convert2Binary(num1, 8) //minuend
122  const bin2flip = convert2Binary(~num2, 8) // 1's complement of subtrahend
123  const result1 = binaryAdder(bin1, bin2flip)
124  const result2 = binaryAdder(result1, convert2Binary(1, 8))
125  const result3 = binaryAdder(result2, convert2Binary(256, 9), 1)
126  return convert2Decimal(result3)
127}
128
129const result = subtract(200, 100)

در ادامه آنچه را که برای ساخت بازنمایی کد انجام داده‌ایم را مشاهده می‌کنید. این بازنمایی دقیقی نیست؛ اما تقریباً همان کارکرد را به روشی مشابه اجرا می‌کند.

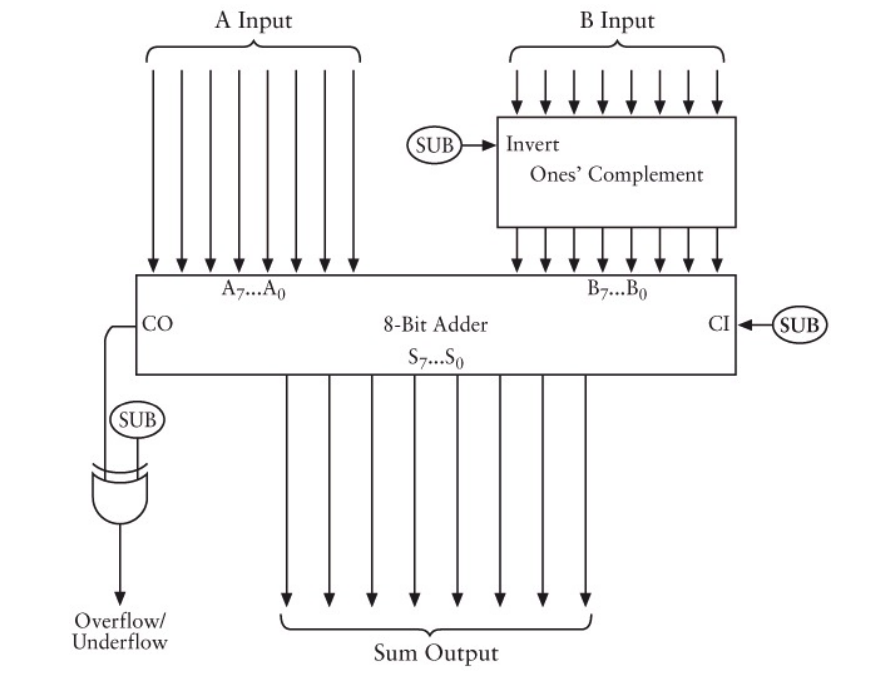
دقت کنید که ورودی B از طریق کادر مکمل 1 که به سیگنال SUB وارد می‌شود گذر می‌کند. سیگنال SUB یا 0 و یا 1 است. اگر 0 باشد ورودی B معکوس نمی‌شود و برعکس. ما این وضعیت را با استفاده از پارامتر operationBit که به تابع binaryAdder ارسال می‌کنیم شبیه‌سازی کرده‌ایم.

سخن پایانی

بدین ترتیب موفق شدیم روش اجرای عملیات ریاضی از سوی رایانه‌ها را درک کنیم. در این مطلب با بازنمایی یک جمع کننده دودویی به صورت کد آشنا شدیم. جمع کننده دودویی ما اعمال جمع و تفریق اعداد را با شبیه‌سازی گیت‌های منطقی اجرا می‌کند که البته ساده‌سازی‌های زیادی روی آن صورت گرفته است.

شما می‌توانید تلاش کنید تا شیوه بازنمایی ضرب و تقسیم را با استفاده از گیت‌های منطقی در کدهای جاوا اسکریپت شبیه‌سازی کنید. توجه داشته باشید که این دو عملیات بسیار پیچیده‌تر هستند؛ اما به هر حال برای علاقه‌مندان به این موضوع، یک تمرین جذاب محسوب می‌شوند.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های مهندسی نرم افزار
• آموزش مروری مدارات منطقی
• مجموعه آموزش‌های دروس مهندسی کامپیوتر
• مجموعه آموزش های مدارهای منطقی (طراحی دیجیتال)
• آموزش مبانی منطق و نظریه مجموعه ها
• آموزش منطق ترکیبی — مجموعه مقالات جامع وبلاگ فرادرس

==