میانگین هندسی – به زبان ساده
«میانگین هندسی» (Geometric Mean)، یکی از انواع میانگین است که برای محاسبه متوسط نرخ رشد (رشد جمعیت یا درصد سود) استفاده میشود. همچنین به منظور محاسبه میانگین برای مقادیری که با مرتبههای متفاوت درجهبندی شدهاند از میانگین هندسی استفاده میشود.


میانگین هندسی و محاسبه آن
اگر بخواهیم عملکرد شرکت را براساس دو پارامتر مانند حفظ محیط زیست (رتبهبندی از ۰ تا ۵) و شفافیت مالی (رتبهبندی از ۰ تا ۱۰۰) ارزیابی کنیم، باید میانگین این پارامترها را بدست آوریم تا بتوانیم عملکرد کلی شرکت را توسط یک عدد بیان کنیم. اگر از میانگین حسابی برای این کار استفاده شود، با توجه به بزرگ بودن مقادیر رتبهها برای شفافیت مالی، اهمیت این پارامتر بیشتر شده و وزن بیشتری به شفافیت مالی برای محاسبه میانگین، داده خواهد شد.
اگر در رتبهبندی شفافیت مالی شرکت کمی کاهش بوجود آید (مثلا از ۹۰ به ۸۰ تبدیل شود) تاثیر این تغییر در میانگین حسابی برای این دو پارامتر زیاد خواهد بود در حالی که تغییر بزرگ در رتبه حفظ محیط زیست (مثلا از ۲ به ۵) تاثیر ناچیزی در میانگین حسابی خواهد گذاشت. استفاده از میانگین هندسی این وزنها (اهمیتها) را نرمال میکند و هر یک از پارامترها اهمیت یکسانی در محاسبه متوسط مقادیر خواهند داشت.
شیوه محاسبه میانگین هندسی که با نماد G نشان داده میشود، به شکل زیر است:
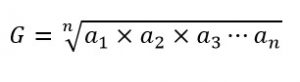
براساس این فرمول کافی است مراحل زیر طی شود:
- همه مقادیر در هم ضرب شوند.
- ریشه nام حاصلضرب محاسبه شود.
به این ترتیب برای محاسبه میانگین هندسی مقادیر 1،5،8،10 بر اساس مراحلی که در بالا گفته شد، به صورت زیر عمل میکنیم:
که با گرفتن ریشه چهارم به مقدار 4.47 خواهیم رسید. در حالیکه میانگین حسابی برای این اعداد برابر با ۶ خواهد بود. برای درک بهتر مفهوم میانگین هندسی به مثالهای زیر توجه کنید.

مثال اول
حقوق ساعتی فردی در طی ۱۰ سال از 2000 تومان به ۵000 تومان رسیده است. متوسط رشد درآمد این فرد براساس میانگین هندسی محاسبه میشود.
ابتدا رشد را محاسبه میکنید.
واضح است که صورت میزان افزایش و مخرج مبنای افزایش را نشان داده است. پس نرخ رشد در این ۱۰ سال، برابر با 2٫۵ است. حال که در ۱۰ سال این اتفاق رخ داده است، متوسط این نرخ رشد همان میانگین هندسی مقدار 2٫۵ خواهد بود.
پس اگر بخواهیم حقوق او را در سال یازدهم محاسبه کنیم، خواهیم داشت:
به جدول زیر توجه کنید:
| سال | حقوق | میزان افزایش نسبت به سال اول | میزان افزایش نسبت به سال قبل | درصد افزایش |
| 0 | 2000 | - | - | - |
| 1 | 2191٫9165 | 191٫9165 | 191٫9165 | 0٫095958 |
| 2 | 2402٫2489 | 402٫2489 | 210٫3324 | 0٫095958 |
| 3 | 2632٫7644 | 632٫7644 | 230٫5155 | 0٫095958 |
| 4 | 2885٫3998 | 885٫3998 | 252٫6354 | 0٫095958 |
| 5 | 3162٫2777 | 1162٫2777 | 276٫8778 | 0٫095958 |
| 6 | 3465٫7242 | 1465٫7242 | 303٫4466 | 0٫095958 |
| 7 | 3798٫2890 | 1798٫2890 | 332٫5647 | 0٫095958 |
| 8 | 4162٫7660 | 2162٫7660 | 364٫4771 | 0٫095958 |
| 9 | 4562٫2177 | 2562٫2177 | 399٫4516 | 0٫095958 |
| 10 | 5000٫0000 | 3000٫0000 | 437٫7823 | 0٫095958 |
| 11 | 5479٫7911 |
همانطور که مشخص است، درصد افزایش سال بعد نسبت به قبل (ستون آخر جدول بالا)، همیشه ثابت بوده ولی میزان افزایش (برحسب تومان) متغیر است.
مثال دوم
سهام یک شرکت در سال اول ۵۰٪، در سال دوم 20٪ و در سال سوم ۹۰٪ رشد داشته است. پس در سال اول ارزش سهام شرکت ۱.۵ برابر و در انتهای سال دوم ۱.۲ برابر سال اول و در پایان سال سوم نیز ۱.۹ برابر سال دوم خواهد بود. متوسط رشد سهام این شرکت به کمک میانگین هندسی محاسبه میشود.
این مقدار نشان میدهد که رشد متوسط ارزش سهام در هر سال برابر با 1.50637 است. در حالیکه با استفاده از میانگین حسابی متوسط رشد ارزش سهام برابر با 1.533 خواهد بود.
حال اگر در پایان این سه سال بخواهیم ارزش سهام شرکت را محاسبه کنیم کافی است به صورت زیر عمل کنیم. فرض بر این است که در سال اول ارزش سهام ۱۰۰۰ ریال است!
ارزش سهام در پایان سال سوم =
البته این محاسبه را میتوان سالانه نیز انجام داد که نتیجه یکسانی خواهد داشت.
- ارزش سهام در انتهای سال اول = 1000 × 1.5 = 1500
- ارزش سهام در انتهای سال دوم = 1500× 1.2 = 1800
- ارزش سهام در انتهای سال سوم = 1800 × 1.9 = 3420
همانطور که در مثالها دیده شد، میانگین هندسی از میانگین حسابی کمتر است که البته میتوان ثابت کرد این موضوع همیشه برقرار است. ولی اگر همه مقدارها یکسان باشند، میانگین هندسی با میانگین حسابی برابر خواهد بود.
نکته: میانگین هندسی فقط برای اعداد مثبت قابل محاسبه است.
آزمون میانگین هندسی
۱. کدام ویژگی میانگین هندسی باعث میشود این روش برای دادههایی با مقیاس سنجش متفاوت نسبت به میانگین حسابی کاربرد بهتری داشته باشد؟
مقدار هر داده را بر اساس قدر مطلق آن میسنجد.
نتیجه همیشه کمتر از میانگین حسابی خواهد بود.
هر پارامتر تاثیر یکسان بر نتیجه دارد و تعادل بین مقیاسها ایجاد میکند.
همه دادهها را با هم جمع میکند تا تاثیر دامنهها بیشتر شود.
میانگین هندسی باعث میشود هر پارامتر تاثیر یکسانی بر نتیجه داشته باشد، حتی اگر دادهها مقیاس متفاوتی داشته باشند. این ویژگی بر خلاف میانگین حسابی است که اگر دامنه عددی برخی پارامترها بزرگتر باشد، همانها تاثیر بیشتری بر میانگین نهایی میگذارند. جمع کردن همه دادهها یا سنجش بر حسب قدر مطلق ویژگی میانگین حسابی یا هندسی نیست و کمتر بودن نتیجه نسبت به میانگین حسابی هم همیشه دلیل کاربردپذیری برای مقیاسهای مختلف نیست.
۲. برای محاسبه دقیق متوسط درصد رشد سالیانه سرمایه در شرایطی که نرخ رشد هر سال متفاوت باشد، کدام نوع میانگین باید انتخاب شود و دلیل آن چیست؟
انتخاب بزرگترین نرخ رشد سالانه برای دقت بیشتر
استفاده از کوچکترین نرخ رشد سالانه برای جلوگیری از ریسک
استفاده از میانگین هندسی چون تاثیر هر سال یکسان در نظر گرفته میشود.
انتخاب میانگین حسابی چون محاسبه آن سادهتر است.
وقتی نرخ رشد سرمایه در هر سال متفاوت است، اگر میانگین حسابی به کار رود، سالهایی با نرخ بالاتر تاثیر بیشتری میگذارند و نتیجه واقعبینانه نیست. اما با استفاده از میانگین هندسی، رشد مرکب سرمایه به درستی محاسبه میشود و هر سال نقش یکسانی دارد. گزینههای دیگر مانند میانگین حسابی یا انتخاب بزرگترین و کوچکترین نرخ رشد، نمایندگی دقیقی از رشد واقعی سرمایه مرکب ارائه نمیکنند.













اگر در یک دوره ۱۲ ساله نرخ تورم به ترتیب ۲۱٪و ۴۴٪ باشد میانگین نرخ تورم در دوره مزبور چقدر است؟ میتونید کمکم کنید
با سلام
نحوه محاسبه میانین هندسی برای اعداد فازی چونه است؟
اگر چندین عدد فازی داشته باشیم چطوری باید از این اعداد میانگین هندسی گرفت؟
سلام
یه سوال وقتی رشد منفی داریم
مثلا در مثال دوم اگه سال اول ۵۰٪ منفی و سال دوم ۵۰٪ مثبت باشه
قیمت سهام در محاسبه حسابی و هندسی اختلاف زیادی دارن
چرا؟
سلام وقت بخیر
در مثال دوم که سهام شرکت در سال اول 50 درصد است، بر چه اساسی ارزش سهام آن سال 1.5 برابر میشه؟ یعنی ارزش سهام اولیه یک (1) در نظر گرفته میشه؟ اگه اینجوریه چرا در محاسبات 1000 گرفته شده؟
با سلام
حقیر فکر میکنم در مثال اول، نرخ رشد اشتباه محاسبه شده است
اگر میزان رشد 10سال را حساب کنیم و سپس میانگین هندسی در 10 سال گرفته شود احتمالا صحیح تر است یعنی:
رشد 10 ساله= 20000/(2000-5000)= 1.5
متوسط رشد= ریشه دهمِ عدد 1.5= 1.041
سلام همراه عزیز مجله فرادرس،
کاملا حق با شماست. باید نوشته می شد، متوسط افزایش حقوق این شخص در این سالها چقدر است. بنا به نظر شما، متن اصلاح شد.
از اینکه مشکلات ما را تذکر میدهید، سپاسگزاریم.
موفق و تندرست باشید.
اگه دارای فراوانی باشن چیکار کنیم ؟
درود بر شما یار فرادرس،
همانطور که در میانگین حسابی، هر مقدار را در تعداد فراوانیهای آن ضرب میکنیم، برای میانگین هندسی نیز هر مقدار را به توان فراوانی آن رسانده و محاسبه میانگین هندسی را دنبال میکنیم. توجه داشته باشید که مجموع فراوانیها باید با n برابر باشد.
از اینکه همراه مجله فرادرس هستید بر خود می بالیم.
تندرست و شاد و پیروز باشید.
با سلام
احتراما ضمن تشکر و سپاس از زحمات شما
در محاسبات حقوق فرد در طی ۱۰ سال از ۲۰۰۰ به ۵۰۰۰ ضرب دو عدد صحیح زیر رادیکال ده میلیون خواهد شد که تبعا وقتی از رادیکال خارج شود ۳۱۶۲.۲۸ خواهد شد
درصورتیکه اشتباه تایپی یک میلیون شده و وقتی از زیر رادیکال بیرون آوریم میشود ۱۰۰۰ که برای خیلی از مراجعه کنندگان مشکل ایجاد میکند مگر اینکه خود شخص محاسبات را انجام داده به مشکل پی ببرد
اما فیلم آموزشی این مشکل رو حل کرده است
از مطالب آموزنده سپاسگزارم
سلام و درود
بله متاسفانه یک صفر در محاسبات کم بود که باعث بوجود آمدن اشکال در خواندن مطلب شده بود.
تصحیح با توجه به نظر شما انجام شد.
با تشکر فراوان از توجه شما به مطالب فرادرس
سلام 2 تا سوال اولا چرا همینطور 90رو کردین 80 دوم اون 1000 تو مثال دوم از کجا اومد
سلام و درود
معمولا عرضه اولیه سهام در بورس، ۱۰۰۰ ریال هست به همین دلیل در مثال ۲، ارزش اولیه را ۱۰۰۰ ریال در نظر گرفته ایم و نشان دادهایم که در پایان سه سال با توجه به رشد متوسط، ارزش سهام شرکت چقدر است!
در بخش متن هم که ۹۰ به ۸۰ تبدیل شده، فرض کردهایم که در شاخص شفافیت مالی شرکت، کاهش وجود داشته از این شاخص از ۹۰ به ۸۰ رسیده است.
باز هم از اینکه همراه و همگام با مجله فرادرس هستید سپاسگزاریم
موفق باشید.