روش یافتن موارد تکراری در آرایه ها — به زبان ساده

در این نوشته قصد داریم یکی از مسائلی را که در موارد متعددی هنگام برنامه‌نویسی ممکن است با آن مواجه شویم بررسی کنیم. در بسیاری از موقعیت‌ها لازم می‌شود که موارد تکراری در آرایه‌ها را بیابیم. در ادامه به بیان دقیق مسئله و روش‌های ممکن برای حل آن می‌پردازیم.

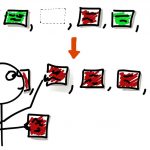
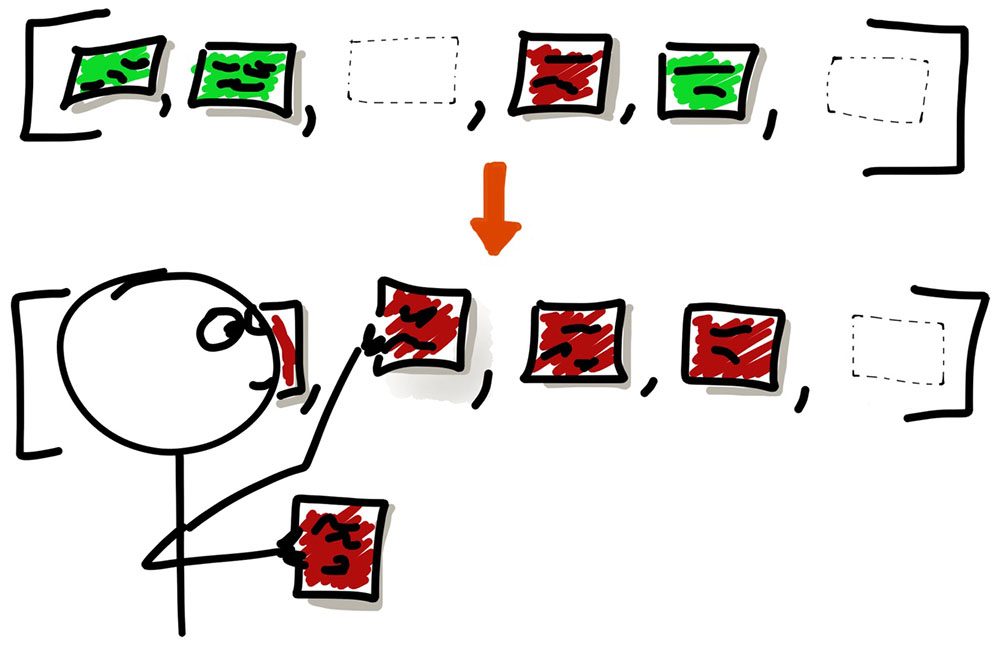
مسئله: یافتن موارد تکراری در آرایه‌ها

فرض کنید آرایه‌ای با n + 1 عضو عدد صحیح بین 1 تا n وجود دارد و ما باید یک عضو تکراری را پیدا کنیم. اگر چند عضو تکراری وجود داشته باشند، باید یکی از آن‌ها را بازگشت دهیم و اگر هیچ عضو تکراری وجود نداشته باشد، باید مقدار 1- را بازگشت دهیم.

فیلم آموزش ساختمان داده ها در فرادرس

کلیک کنید

مثال

ورودی: [1, 2, 2, 3]

خروجی: 2

ورودی: [3, 4, 1, 4, 1]

خروجی: 4 یا 1

فرایند حل مسئله

پیش از آن که به مشاهده راه‌حل‌ها بپردازیم، ابتدا کمی در مورد مسئله صحبت می‌کنیم. می‌دانیم که آرایه‌ای به طور n +1 از اعداد صحیح بین 1 تا n داریم.

فیلم آموزش آرایه در ساختمان داده ها (مرور – تست کنکور ارشد) (رایگان) در فرادرس

کلیک کنید

برای نمونه در آرایه‌ای با 5 عضو به صورت عدد صحیح این تعریف بدان معنی است که هر عدد صحیح مقداری بین 1 تا 4 دارد. یعنی به طور خودکار دست‌کم یک مورد تکراری وجود دارد. تنها استثنا در حالت آرایه با اندازه 1 است. این تنها موردی است که باید مقدار 1- بازگشت داده شود.

Brute Force

در روش حل Brute Force باید از حلقه‌های تو در تو به صورت زیر استفاده کنیم:

for i = 0; i < size(a); i++ {
  for j = i+1; j < size(a); j++ {
    if(a[i] == a[j]) return a[i]
  }
}

پیچیدگی زمانی این راه‌حل (O(n² و پیچیدگی فضایی آن برابر با (O(1 است.

شمارش تکرارها

راه‌حل دیگر این است که ساختمان داده‌ای داشته باشیم که تعداد تکرارها روی هر عدد صحیح را بشمارد. این راه‌حل را می‌توان با استفاده از یک آرایه یا با استفاده از جدول هَش (hash table) پیاده‌سازی کرد.

پیاده‌سازی این راه‌حل در جاوا به صورت زیر است:

public int repeatedNumber(final List<Integer> list) {
  if(list.size() <= 1) {
    return -1;
  }
  
  int[] count = new int[list.size() - 1];

  for (int i = 0; i < list.size(); i++) {
    int n = list.get(i) - 1;
    count[n]++;

    if (count[n] > 1) {
      return list.get(i);
    }
  }

  return -1;
}

مقدار اندیس i نشان‌دهنده تعداد تکرارهای i+1 است. این راه‌حل پیچیدگی زمانی (O(n دارد؛ اما پیچیدگی فضایی آن برابر با (O(n چون به یک ساختمان داده اضافی نیاز داریم.

آرایه‌های مرتب

اگر از یک تکنیک ساده‌سازی استفاده کنیم، می‌توانیم از آرایه مرتب برای یافتن راه‌حل استفاده کنیم.

در این حالت کافی است هر عنصر را با همسایه سمت راست آن مقایسه کنیم.

پیاده‌سازی این روش در جاوا به صورت زیر است:

public int repeatedNumber(final List<Integer> list) {
  if (list.size() <= 1) {
    return -1;
  }

  Collections.sort(list);

  for (int i = 0; i < list.size() - 1; i++) {
    if (list.get(i) == list.get(i + 1)) {
      return list.get(i);
    }
  }

  return -1;
}

پیچیدگی فضایی این روش (O(1؛ اما پیچیدگی زمانی برابر با ((O(n log(n است، چون در ابتدا باید عناصر آرایه را مرتب کنیم.

مجموع عناصر

یکی از ایده‌ها برای یافتن موارد تکراری، ایده جمع زدن همه عناصر آرایه و مقایسه آن با مجموع 1 + 2 + … + n است.

مثالی از آن به صورت زیر است:

Input: [1, 4, 3, 3, 2, 5]
Sum = 18
As in this example, we have n = 5:
Sum of 1 to 5 = 1 + 2 + 3 + 4 + 5 = 15
=> 18 - 15 = 3 so 3 is the duplicate

در این مثال، می‌توانیم راه‌حلی با پیچیدگی زمانی (O(n و پیچیدگی فضایی (O(1 به دست آوریم. با این حال این راه‌حل تنها در مواردی پاسخگو است که تنها یک مورد تکراری وجود داشته باشد. مثال نقض آن چنین است:

Input: [1, 2, 3, 2, 3, 4]
Sum = 15
As in this example we have n = 5,
Sum of 1 to 5 = 1 + 2 + 3 + 4 + 5 = 15
/!\ Not working

در این صورت به نتیجه‌ای نمی‌رسیم. اما برخی اوقات لازم است راه‌حل‌های مختلف را امتحان کنیم تا بهترین راه‌حل را بیابیم.

نشانه‌گذاری (Marker)

نکته جالبی وجود دارد که باید اینجا اشاره کنیم. راه‌حل‌هایی که تاکنون بررسی کردیم، عملاً از این واقعیت که هر عدد صحیح در بازه بین 1 و n قرار دارد استفاده نکرده‌اند. به دلیل همین محدودیت جالب، هر مقدار اندیس متناظر خود را در آرایه دارد.

در این راه‌حل، این آرایه خاص را به صورت یک لیست پیوندی در نظر می‌گیریم و هر اندیس به مقدار یک اندیس اشاره دارد:

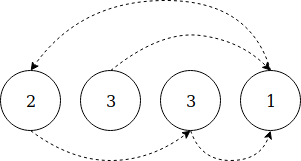
بدین ترتیب با چرخش روی همه عناصر آرایه و نشانه‌گذاری اندیس متناظر آن به صورت منفی، می‌توانیم مسئله را حل کنیم. اگر مقداری را قبلاً به صورت منفی نشانه‌گذاری کرده باشیم، بدین معنی است که اندیس آن تکراری است.

مثال گام به گام زیر این روش را به تفصیل توضیح داده است:

Input: [2, 3, 3, 1]
* Index 0:
    Absolute value = 2
    Put a minus sign to a[2] => [2, 3, -3, 1]
* Index 1:
    Absolute value = 3
    Put a minus sign to a[3] => [2, 3, -3, -1]
* Index 2:
    Absolute value = 3
    As a[3] is already negative, it means 3 is a duplicate

پیاده‌سازی این راه‌حل در زبان برنامه‌نویسی جاوا به صورت زیر است:

public int repeatedNumber(final List<Integer> list) {
  if (list.size() <= 1) {
    return -1;
  }

  for (int i = 0; i < list.size(); i++) {
    if (list.get(Math.abs(list.get(i))) > 0) {
      list.set(Math.abs(list.get(i)), -1 * list.get(Math.abs(list.get(i))));
    } else {
      return Math.abs(list.get(i));
    }
  }

  return 0;
}

پیچیدگی زمانی این راه‌حل (O(n و پیچیدگی فضایی آن (O(1 است. با این وجود این راه‌حل نیازمند دستکاری لیست ورودی است.

تکنیک رانر (Runner)

راه‌حل دیگری نیز وجود دارد که در آن آرایه مفروض را به صورت نوعی لیست پیوندی در نظر می‌گیریم. در این حالت نیز دلیل این که می‌توانیم چنین کاری بکنیم این است که همه مقادیر بین 1 و n قرار دارند. فرض کنید می‌خواهیم مثال [1, 2, 3, 4, 2] را بررسی کنیم:

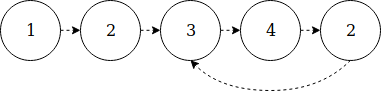
در این بازنمایی، زمانی می‌توانیم بگوییم یک مورد تکراری وجود دارد که چرخه‌ای وجود داشته باشد. به علاوه، مورد تکراری نقطه ورودی چرخه است. در این مثال این نقطه در عنصر دوم آرایه قرار دارد. با الهام گرفتن از الگوریتم یافتن چرخه فلوید، می‌توان الگوریتم زیر را تنظیم کرد:

• دو اشاره‌گر slow و fast را مقداردهی اولیه می‌کنیم.
• در هر مرحله، slow هر بار یک گام به صورت [slow = a[slow حرکت می‌کند، در حالی که fast هر بار دو گام به صورت [[fast = a[a[fast حرکت می‌کند.
• وقتی slow == fast شود، درمی‌یابیم که با یک مورد تکراری مواجه شده‌ایم.

البته این الگوریتم هنوز کامل نیست. نقطه ورودی این چرخه همان مورد تکراری خواهد بود. ما باید slow را ریست کنیم و هر دو اشاره‌گر را به صورت گام به گام حرکت دهیم تا این که دوباره با هم برابر شوند.

یکی از پیاده‌سازی‌های ممکن این الگوریتم در زبان جاوا به صورت زیر است:

public int repeatedNumber(final List<Integer> list) {
  if (list.size() <= 1)
    return -1;

  int slow = list.get(0);
  int fast = list.get(list.get(0));

  while (fast != slow) {
    slow = list.get(slow);
    fast = list.get(list.get(fast));
  }

  slow = 0;
  while (fast != slow) {
    slow = list.get(slow);
    fast = list.get(fast);
  }
  return slow;
}

پیچیدگی زمانی این راه‌حل برابر با (O(n و پیچیدگی فضایی آن (O(1 است و الزامی به دستکاری لیست ورودی وجود ندارد.

فیلم مجموعه آموزش ساختمان داده و طراحی الگوریتم – از دروس دانشگاهی تا کاربردی در فرادرس

کلیک کنید

اگر این مطلب برای شما مفید بوده است، پیشنهاد ما استفاده از منابع زیر است:

• مجموعه آموزش‌های مهندسی نرم افزار
• معرفی مبانی ساختار داده و آرایه های داده ای — به زبان ساده
• مجموعه آموزش های پروژه محور برنامه نویسی
• آموزش آرایه در ساختمان داده
• آرایه های PHP — به زبان ساده
• آموزش آرایه ها در زبان برنامه نویسی C
• آموزش معرفی و تعریف آرایه ها در تکمیلی پایتون

==