احتمال – مثبت کاذب و منفی کاذب
در این آموزش در رابطه با احتمال و مثبت و منفی کاذب صحبت خواهیم کرد.
نتیجه آزمایش می گوید "بله"... آیا واقعا جواب "بله" هست؟
وقتی یک تست دارید که می گوید "بله" یا "نه" (مانند یک تست پزشکی)، باید به این فکر کنید که:
- ممکن است پاسخ "بله" غلط باشد.
- ممکن است پاسخ "نه" غلط باشد.
غلط؟
مانند این است که به شما بگویند کاری را انجام داده اید در صورتی که چنین نیست!
یا شاید با این که انجام داده اید فکر کنید انجام نداده اید.
اسم های خاصی برای این امور وجود دارد، به نام های "مثبت کاذب"(False positive) و "منفی کاذب"(False negative):

اینجا برخی از مثال های "مثبت های کاذب" و "منفی های کاذب" را مطرح می کنیم:
- بخش امنیت فرودگاه: یک "مثبت کاذب" هنگامی است که اشیاء معمولی مانند کلیدها و یا سکه ها به اشتباه اسلحه تشخیص داده می شوند (و ماشین صدای "بیپ" را ایجاد می کند)
- کنترل کیفیت: یک "مثبت کاذب" هنگامی است که محصول با کیفیت خوب، مردود می شود و یک "منفی کاذب" هنگامی است که محصول بی کیفیت مورد قبول واقع می شود
- نرم افزار ضد ویروس: یک "مثبت کاذب" هنگامی است که یک فایل عادی بعنوان یک ویروس شناخته می شود
- آزمایش پزشکی: گرفتن آزمایش های ارزان قیمت و بررسی آن توسط تعداد زیادی از پزشکان می تواند مثبتهای کاذب زیادی به بار آورد (یعنی جواب تست بگوید که بیمار هستید در حالی که چنین نیست)، و سپس خواسته شود که دوباره آزمایش های با دقت بیشتر بگیرید.
اما بسیاری از مردم واقعیت در پشت "بله" یا "نه" را نمی دانند، مانند این مثال:
مثال: این حساسیت است یا نه؟

شکارچی می گوید که این گربه باعث خارش من می شود. آزمایشی برای حساسیت نسبت به گربه ها وجود دارد، اما این آزمایش همواره درست نیست:
- برای مردمی که واقعا حساسیت دارند، جواب آزمایش در %80 مواقع "بله" است
- برای مردمی که حساسیت ندارند، جواب آزمایش در %10 مواقع "بله" است ("مثبت کاذب")
جدول آن در زیر رسم شده:

سوال: اگر %1 از جمعیت حساسیت داشته باشند، و جواب آزمایش گرفته شده از این شکارچی "بله" باشد، چه مقدار ممکن است که شکارچی واقعا حساسیت داشته باشد؟
بنظرتان %75؟ یا شاید %50؟
آزمایش مشابهی گرفته شد و در اختیار چندین دکتر قرار گرفت و بیشترشان اطراف %75 حدس زدند ...
... اما کاملا اشتباه می کردند!
(منبع:”Probabilistic reasoning in clinical medicine: Problems and opportunities” by David M. Eddy 1982 که این مثال از این کتاب برداشته شده است)
دو راه حل خوب برای درک این مسئله وجود دارد: "1000 تا در نظر بگیرید" و "نمودار درختی"
1000 نفر مردم را در نظر بگیرید
وقتی که می خواهید سوالاتی از این قبیل را درک کنید، یک گروه بزرگتر (مثلا 1000 تا) در نظر بگیرید و با اعداد کارتان را ردیف کنید!:
- از 1000 نفر، فقط 10 نفر واقعا حساسیت دارند (%1 از 1000 نفر برابر 10 است)
- تست برای مردمی که حساسیت دارند، %80 صحت دارد، پس از آن 10 نفر 8 نفر می ماند.
- و از این طرف، 990 نفر حساسیت ندارند، ولی جواب آزمایش برای %10 از آنها "بله" خواهد بود؛ که برابر 99 نفر از مردم است که به اشتباه جواب "بله" دریافت می کنند (مثبت کاذب)
- پس از 1000 نفر مردم، (8 + 99) = 107 نفر پاسخ "بله" را از آزمایش دریافت می کنند
روی جدول:
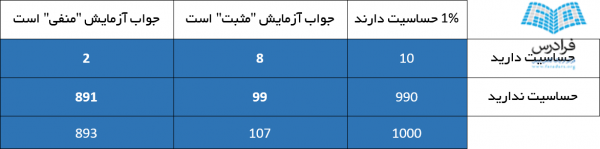
پس 107 نفر پاسخ "بله" می گیرند در حالیکه فقط 8 نفر از آنها واقعا حساسیت دارند:
8 / 107 = 7% حدودا
پس، اگرچه پاسخ آزمایش شکارچی "بله" بود، تنها %7 احتمال دارد که شکارچی واقعا حساسیت به گربه ها داشته باشد.
بعنوان یک درخت
رسم یک نمودار درختی واقعا به دردمان خواهد خورد:
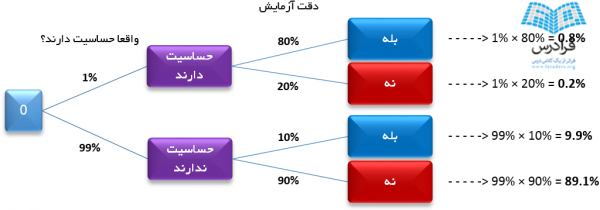
قبل از هر چیزی، بررسی می کنیم که هنگام جمع کردن، درصدی از قلم نیوفتاده باشد:
0.8% + 0.2% + 9.9% + 89.1% = 100%
خوب است...
و دو جواب "بله" جمع می شوند به %10.7 = %9.9 + %0.8، در حالی که فقط %0.8 صحیح است.
0.8 / 10.7 = 7%
همان پاسخ بالایی
نتیجه گیری
هنگام رو در رو شدن با مثبت های کاذب و منفی های کاذب (یا سایر سوال های گمراه کننده احتمال) از روش های زیر برای روشن شدن مسئله کمک بگیرید:
- فرض کنید 1000 تا (از هر چیزی) دارید
- یا یک نمودار درختی تشکیل دهید











