معرفی الگوریتم های مجانبی، حریصانه و برنامه نویسی دینامیک – به زبان ساده
الگوریتم به رویههای گام به گام گفته میشود که مجموعهای از دستورالعملها برای اجرا با ترتیب خاص در جهت رسیدن به یک خروجی مطلوب است. الگوریتمها به طور کلی مستقل از زبان ایجاد میشوند، یعنی یک الگوریتم میتواند در چندین زبان برنامهنویسی پیادهسازی شود. در این نوشته برخی الگوریتم های بسیار مهم در زمینه ساختار داده مانند الگوریتم مجانبی و حریصانه بررسی شدهاند. برخی الگوریتمهای مهم از نقطه نظر ساختار داده در ادامه ارائه شده است:


- جستجو: این الگوریتم در یک ساختار داده، آیتمی را جستجو میکند.
- مرتبسازی: این الگوریتم آیتمها را با نظم مشخصی مرتب میکند.
- درج: الگوریتمی برای درج یک آیتم در یک ساختار داده است.
- بهروزرسانی: از این الگوریتم برای بهروزرسانی یک آیتم موجود در یک ساختار داده استفاده میشود.
- حذف: همان طور که از نامش مشخص است این الگوریتم برای حذف یک آیتم موجود در یک ساختار داده مورد استفاده قرار میگیرد.
خصوصیات یک الگوریتم
همه رویهها را نمیتوان الگوریتم دانست. یک الگوریتم باید خصوصیات زیر را داشته باشد:
- بیابهام باشد: الگوریتم باید واضح و بدون ابهام باشد. در هر یک از مراحل الگوریتم، ورودیها و خروجیهای باید مشخص بوده و تنها یک معنی واحد داشته باشند.
- دارای ورودی: یک الگوریتم باید 0 یا چند ورودی خوشتعریف داشته باشد.
- دارای خروجی: الگوریتم باید 1 یا چند خروجی خوشتعریف داشته و این خروجی نیز باید با خروجی مطلوب همخوانی داشته باشد.
- متناهی بودن: الگوریتمها باید پس از تعداد مشخصی از مراحل به پایان برسند.
- دسترسیپذیری: الگوریتمها باید با منابع موجود قابل دسترس باشند.
- مستقل بودن: یک الگوریتم باید جهتگیری گام به گامی داشته باشد که مستقل از کد برنامهنویسی باشد.
چگونه یک الگوریتم بنویسیم؟
استاندارد کاملاً تعریف شدهای برای نوشتن یک الگوریتم وجود ندارد و بیشتر به نوع مسئله و منابع مربوط است. الگوریتمها هرگز به طور خاص برای یک کد برنامهنویسی نوشته نمیشوند.
همان طور که میدانیم همه زبانهای برنامهنویسی سازههای ابتدایی مشترکی مانند حلقه (Do، For، While)، کنترل گردش (if-else) و موارد دیگر را دارند. از این سازههای مشترک میتوان برای نوشتن الگوریتم کمک گرفت.
گفتیم که الگوریتمها به روش گام به گام نوشته میشوند؛ اما همواره نیز چنین نیست. نگارش الگوریتم یک فرایند است و پس از این که دامنه مسئله به طور کامل تعریف شد، صورت میگیرد. یعنی ما باید حتماً دامنه مسئلهای را که میخواهیم راهحلی برای آن طراحی کنیم، بدانیم.
مثال
در این بخش شیوه نگارش الگوریتم ر با یک مثال بررسی میکنیم. فرض کنید مسئله ما چنین است که میخواهیم یک الگوریتم طراحی کنیم تا دو عدد را با هم جمع کرده و نتیجه را نمایش دهد:
- گام 1: آغاز
- گام 2: سه عدد صحیح به صورت a، b و c تعریف میکنیم
- گام 3: مقادیر a و b را تعریف میکنیم
- گام 4: مقادیر a و b را با هم جمع میکنیم
- گام 5: خروجی گام 4 را در متغیر c ذخیره میکنیم
- گام 6: c را پرینت میکنیم
- گام 7: توقف
الگوریتمها شیوه نوشتن برنامه را برای برنامه نویسان مشخص میکنند. الگوریتم فوق را میتوانیم به صورت زیر نیز بنویسیم:
- گام 1: آغاز جمع
- گام 2: دریافت مقادیر a و b
- گام 3: c ← a + b
- گام 4: نمایش c
- گام 5: توقف
در مسائل مربوط به طراحی و تحلیل الگوریتمها معمولاً روش دوم برای توصیف یک الگوریتم مورد استفاده قرار میگیرد. بدین ترتیب با حذف تعریفهای غیر ضروری امکان تحلیل الگوریتم برای تحلیلگر آسانتر میشود. تحلیلگر در این وضعیت میتواند ببیند که چه عملیاتهایی صورت گرفته و گردش فرایند به چه ترتیب است. نوشتن شماره گامها اختیاری است. ما برای دریافت راهحل یک مسئله مفروض الگوریتمی نوشتهایم. یک مسئله میتواند به روشهای مختلفی حل شود.
از این رو الگوریتمهای راهحل مختلفی میتوانند برای یک مسئله وجود داشته باشند. مرحله بعدی تحلیل این الگوریتمهای مختلف راهحل و پیادهسازی بهترین راهحل ممکن است.
تحلیل الگوریتم
بازده یک الگوریتم را میتوان در دو مرحله مختلف تحلیل کرد، پیش از پیادهسازی و پس از پیادهسازی:
- تحلیل پیشینی (A Priori): این یک تحلیل نظری از الگوریتم است. بازدهی یک الگوریتم بر اساس این فرض که همه عاملهای دیگر، برای مثال سرعت پردازنده ثابت هستند و هیچ تأثیری روی پیادهسازی ما ندارند، صورت میگیرد.
- تحلیل پسینی (A Posterior): یک تحلیل عملی از الگوریتم است. الگوریتم مورد نظر با استفاده از یک زبان برنامهنویسی پیادهسازی میشود. سپس بر روی یک رایانه هدف به اجرا در میآید. در این نوع تحلیل، آمار واقعی مانند زمان اجرا و فضای حافظه مورد نیاز گردآوری میشوند.
در مورد تحلیلهای پیشینی الگوریتم در ادامه بیشتر صحبت خواهیم کرد. تحلیل الگوریتم به زمان اجرای عملیاتهای مختلف بستگی دارد. زمان اجرای یک عملیات را میتوان بر اساس تعداد دستورالعملهای رایانهای برای هر عملیات تعریف کرد.
پیچیدگی الگوریتم
فرض کنید X یک الگوریتم و n اندازه دادههای ورودی باشد، در این صورت زمان و فضای مورد نیاز از سوی الگوریتم x دو عامل عمده هستند که بازدهی آن را تعیین میکنند:
- عامل زمان: زمان بر اساس شمارش تعداد عملیاتهایی کلیدی مانند تعداد مقایسه الگوریتمهای مرتبسازی تعیین میشود.
- عامل فضا: فضا بر حسب بیشترین مقدار حافظهای که از سوی الگوریتم مورد نیاز است تعیین میشود.
پیچیدگی یک الگوریتم (f(n زمان اجرا و/یا فضای ذخیرهسازی مورد نیاز از سوی الگوریتم را بر حسب n به عنوان اندازه دادههای ورودی تعیین میکند.
پیچیدگی فضایی
پیچیدگی فضایی یک الگوریتم نشان دهنده مقدار فضای حافظهای است که الگوریتم در طی چرخه عمر خود به آن نیاز دارد. فضای مورد نیاز از سوی الگوریتم برابر با مجموع دو مؤلفه زیر است:
بخش ثابتی از فضای مورد نیاز برای ذخیرهسازی دادهها و متغیرهای مشخص که مستقل از اندازه مسئله هستند. برای نمونه متغیرها و ثابتهای ساده مورد استفاده، اندازه برنامه و غیره.
بک بخش متغیر از فضا که به وسیله متغیرها اشغال میشود. اندازه متغیرها متفاوت است و به اندازه مسئله بستگی دارد. برای نمونه تخصیص دینامیک حافظه، فضای پشته بازگشتی و غیره.
پیچیدگی فضایی (S(pبرای هر الگوریتم p به صورت زیر محاسبه میشود:
(S(P) = C + SP(I
که در آن C بخش ثابت و (S(I بخش متغیر الگوریتم است که به خصوصیات هر نمونه از I بستگی دارد. در ادامه مثال سادهای برای توضیح این مفهوم ارائه شده است:
- الگوریتم: (SUM(A, B
- گام 1: آغاز
- گام 2: C ← A + B + 10
- گام 3: توقف
در این الگوریتم 3 متغیر به نامهای A، B و C داریم. از این رو S(P) = 1+3. اینک فضا به نوع داده هر متغیر و انواع ثابت و تعداد هر کدام بستگی دارد.
پیچیدگی زمانی
پیچیدگی زمانی یک الگوریتم نشان دهنده مقدار زمان مورد نیاز برای اجرای کامل آن الگوریتم است. نیازمندی زمانی به صورت یک تابع عددی (T(n تعریف میشود که در آن (T(n را میتوان به صورت تعداد گامهایی در نظر گرفت که هر گام برای کامل شدن به زمان ثابتی نیاز دارد.
برای نمونه افزودن دو عدد صحیح n-بیتی به n گام نیاز دارد. در نتیجه کل زمان محاسباتی به صورت T(n) = c * n است که در آن c زمان مورد نیاز برای افزودن دو بیت است. میبینیم که (T(n با افزایش اندازه ورودی به صورت خطی رشد میکند.
تحلیل مجانبی (Asymptotic Analysis)
منظور از تحلیل مجانبی یک الگوریتم، تعریف کردن کران/چارچوب ریاضیاتی عملکرد زمان اجرای آن است. با استفاده از تحلیل مجانبی میتوان به خوبی در مورد سناریوهای بهترین حالت، حالت میانی و بدترین حالت اجرای یک الگوریتم تصمیمگیری کرد.
منظور از تحلیل مجانبی یعنی کران ورودی. یعنی اگر هیچ ورودی به الگوریتم نباشد، نتیجه گرفته میشود که الگوریتم در طی زمان ثابتی اجرا میشود. در اینجا به جز ورودی، همه عاملهای دیگر ثابت در نظر گرفته میشوند.
تحلیل مجانبی به محاسبه زمان اجرای هر عملیات در واحدهای ریاضیاتی محاسبه گفته میشود. برای نمونه زمان اجرای یک عملیات به صورت (f(n محاسبه میشود و ممکن است برای عملیات دیگری به صورت (g(n2 باشد. به طور مشابه، اگر n به قدر کافی کوچک باشد، زمان اجرای هر دو عملیات تقریباً برابر خواهد بود. به طور معمول زمان مورد نیاز برای یک الگوریتم در یکی از سه دسته زیر قرار میگیرد:
- بهترین حالت: کمترین زمان مورد نیاز برای اجرای برنامه
- حالت میانگین: زمان میانگین برای اجرای برنامه
- بدترین زمان: بیشترین زمان مورد نیاز برای اجرای برنامه
نمادگذاریهای مجانبی
در ادامه نمادهای متداول مورد استفاده برای تحلیلهای مجانبی جهت محاسبه پیچیدگی زمان اجرای یک الگوریتم ارائه شده است:
- نماد O
نماد Ω
نماد θ
نماد O بزرگ
نمادگذاری (O(n روش رسمی بیان کران بالای زمان اجرای یک الگوریتم است. این تابع پیچیدگی زمانی را در بدترین حالت یا طولانیترین مدت اجرای یک الگوریتم اندازهگیری میکند.
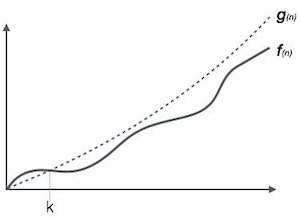
برای مثال برای یک تابع (f(n
Ο(f(n)) = { g(n): there exists c > 0 and n0 such that f(n) ≤ c.g(n) for all n > n0. }
نماد امگا، Ω
نمادگذاری (Ω(n روش رسمی بیان کران پایین زمان اجرای یک الگوریتم محسوب میشود. این تابع پیچیدگی زمانی بهترین حالت یا به عبارت دیگر کمترین زمانی که یک الگوریتم برای پایان یافتن نیاز دارد را اندازهگیری میکند.

برای مثال برای یک تابع (f(n
Ω(f(n)) ≥ { g(n): there exists c > 0 and n0 such that g(n) ≤ c.f(n) for all n > n0. }
نماد تتا θ
نمادگذاری (θ(n روش رسمی بیان هر دو کران بالا و پایین برای زمان اجرای یک الگوریتم است. این تابع به صورت زیر بیان میشود:

θ(f(n)) = { g(n) if and only if g(n) = Ο(f(n)) and g(n) = Ω(f(n)) for all n > n0. }
نمادهای رایج مجانبی
در ادامه فهرستی از برخی نمادگذاریهای رایج مجانبی ارائه شده است:
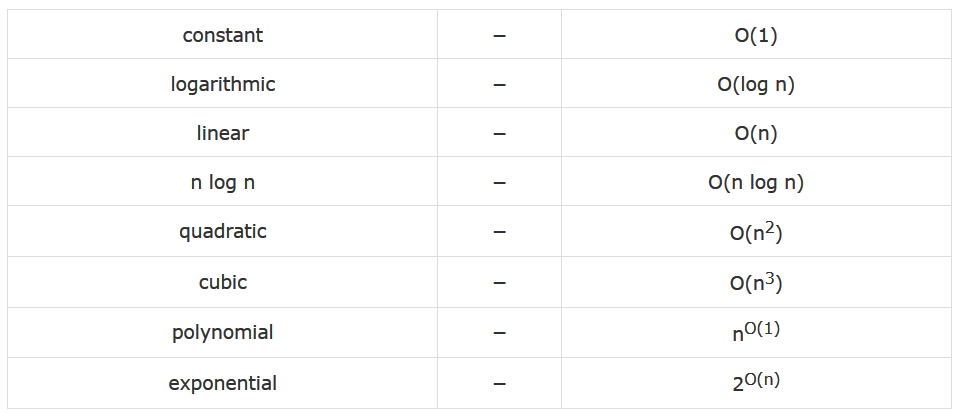
الگوریتمهای حریصانه (Greedy Algorithms)
الگوریتم حریصانه به الگوریتمی گفته میشود که برای رسیدن به بهینهترین راهحل یک مسئله استفاده میشود. در رویکرد الگوریتم حریصانه، تصمیمهایی در یک دامنه راهحل مفروض میگیرد. برای این که یک الگوریتم حریصانه باشد، باید نزدیکترین راهحل که به نظر میرسد بهترین اره حل ممکن است انتخاب شده باشد.
الگوریتمهای حریصانه تلاش میکنند تا بهترین راهحل محلی را بیابند که ممکن است در نهایت منجر به راهحلهای بهینه سراسری شود. با این حال به طور کلی الگوریتمهای حریصانه، راهحلهای بهینه سراسری ارائه نمیکنند. برای این که این وضعیت را بهتر متوجه شوید، یک مثال ارائه میکنیم.
مسئله شمارش سکهها
در این مسئله میخواهیم با کمترین تعداد سکهها، مقدار مشخصی از پول را داشته باشیم. رویکرد حریصانه برای رسیدن به کمترین تعداد سکهها، بزرگترین سکهها را انتخاب میکند. اگر سکههای 1، 2، 5 و 10 ریالی در اختیار ما قرار گرفته باشند و از ما خواسته شده باشد که 18 ریال را ارائه کنیم، در این صورت رویه حریصانه به صورت زیر خواهد بود:
- یک سکه 10 ریالی انتخاب میکنیم و 8 ریال باقی میماند.
- سپس یک سکه 5 ریالی انتخاب میکنیم و 3 ریال باقی میماند.
- سپس یک سکه 2 ریالی انتخاب میکنیم و 1 ریال باقی میماند.
- در نهایت یک سکه 1 ریالی اضافه میکنیم و مسئله ما حل شده است.
با این که الگوریتم فوق به ظاهر به خوبی کار میکند و برای این مبلغ تنها به 4 سکه نیاز داریم؛ اما اگر مسئله را کمی تغییر دهیم، در این صورت، همین رویکرد ممکن است همان نتیجه بهینه را در اختیار ما قرار ندهد.
فرض کنید در یک سیستم پولی ما تنها سکههای 1، 7 و 10 ریالی داریم. این سکهها برای رسیدن به مبلغ 18 ریال بسیار مطلوب است؛ ولی اگر بخواهیم مبلغ 15 را داشته باشیم، ممکن است به سکههایی بیش از حد ضرورت نیاز داشته باشیم. برای مثال رویکرد حریصانه از سکههای 1 + 1 + 1 + 1 + 1 + 10 استفاده میکند که مجموعاً شش سکه هستند. در حالی که رویکرد فوق میتواند مسئله را تنها با 3 سکه حل کند: یعنی 1 + 7 + 7 .
به همین دلیل میتوانیم نتیجه بگیریم که رویکرد حریصانه راهحلهای سریعاً بهینهای را ارائه میدهد؛ ولی ممکن است در یافتن راهحلهای بهینه سراسری مشکلات جدی داشته باشد.
مثال
اغلب الگوریتمهای شبکهای از رویکرد حریصانه استفاده میکنند. در ادامه فهرستی از برخی از آنها را ارائه کردهایم:
- مسئله فروشنده دورهگرد (Travelling Salesman)
- الگوریتم درخت پوشاننده کمینه پریم، (Prim's Minimal Spanning Tree)
- الگوریتم درخت پوشاننده کمینه کروسکال (Kruskal's Minimal Spanning Tree)
- الگوریتم درخت پوشاننده کمینه دکسترا (Dijkstra's Minimal Spanning Tree)
- گراف – رنگآمیزی نقشه (Map Coloring)
- گراف – پوشش گرهی (Vertex Cover)
- مسئله کولهپشتی (Knapsack)
- مسئله زمانبندی تولید کارگاهی (Job Scheduling)
مسائل مشابه زیاد دیگری نیز هستند که از رویکرد حریصانه برای یافتن راهحل بهینه استفاده میکنند.
الگوریتم تقسیم و حل (Divide and Conquer)
در رویکرد تقسیم و حل، مسئلهای که باید حل کنیم به چند مسئله فرعی کوچکتر تقسیم میشود و هر یک از این مسائل به طور مستقل از هم حل میشوند. زمانی که بخواهیم همین مسائل فرعی را دوباره به مسائل خردتر تقسیم کنیم، ممکن است در نهایت به حالتی برسیم که دیگر امکان تقسیم وجود نداشته باشد. این مسئلههای فرعی با کمترین اندازه اتمیک حل میشوند. راهحل همه مسئلههای فرعی در نهایت با هم ادغام میشوند تا راهحل مسئله اصلی به دست آید.

به طور کلی رویکرد «تقسیم و حل» را میتوان در فرایندی سه مرحلهای درک کرد.
تقسیم/تجزیه
این مرحله شامل تجزیه مسئله به مسئلههای فرعی کوچکتر است. مسئلههای فرعی باید نماینده بخشی از مسئله اصلی باشد. این مرحله به طور کلی یک رویکرد بازگشتی برای تقسیم مسئله دارد و تا مرحلهای پیش میرود که دیگر امکان تقسیم بیشتر وجود نداشته باشد. در این مرحله، مسئلههای فرعی ماهیتی اتمیک مییابند؛ اما همچنان نماینده بخشی از مسئله واقعی هستند.
حل کردن
در این مرحله تعداد زیادی از مسئلههای فرعی باید حل شوند. به طور کلی در این مرحله، مسائل به طور مستقل از هم حل میشوند.
ادغام/ترکیب
زمانی که مسئلههای فرعی حل شدند، در این مرحله به طور بازگشتی با هم ترکیب میشوند تا یک راهحل برای مسئله اصلی بیابیم. رویکرد الگوریتمی به طور بازگشتی عمل میکند و مراحل حل و ادغام چنان به هم پیوسته عمل میکنند که به صورت یک جزء واحد به نظر میرسند.
مثال
در ادامه الگوریتمهای رایانهای را ارائه کردهایم که بر مبنای رویکرد برنامهنویسی تقسیم و حل هستند:
- مرتبسازی ادغامی (Merge Sort)
- مرتبسازی سریع (Quick Sort)
- جستجوی دودویی (Binary Search)
- ضرب ماتریس استراسن (Strassen's Matrix Multiplication)
- تعیین نزدیکترین زوج نقاط در فضای دو بعدی (Closest pair points)
روشهای مختلفی برای حل کردن هر مسئله ریاضیاتی وجود دارد؛ اما روشهایی که در بخش فوق مورد اشاره قرار گرفتند، نمونههای خوبی از رویکرد تقسیم و حل هستند.
برنامهنویسی دینامیک
رویکرد برنامهنویسی پویا یا دینامیک مشابه رویکرد «تقسیم و حل» است که در بخش فوق توضیح دادیم و به تجزیه مسئله به اجزای کوچکتر و سپس تقسیم مجدد آنها به اجزای خردتر میپردازد. اما بر خلاف رویکرد تقسیم و حل، این مسئلههای فرعی به طور مستقل از هم حل نمیشوند. بلکه نتایج این مسئلههای فرعی خردتر به خاطر سپرده میشود تا برای مسئلههای خردتر همپوشان، مورد استفاده قرار گیرد.
برنامهنویسی دینامیک زمانی استفاده میشود که با مسائلی سروکار داشته باشیم که بتوان آنها را به مسئلههای مشابه خردتر تقسیم کرد به طوری که نتیجه آنها را بتوان در مواردی برای هم مورد استفاده قرار داد. در اغلب موارد این الگوریتمها برای بهینهسازی مورد استفاده قرار میگیرند. پیش از حل کردن این مسائل فرعی، الگوریتم دینامیک تلاش میکند تا نتایج مسائل فرعی دیگر که قبلاً حل شدهاند را بررسی کند. راهحلهای مسائل فرعی با هم ترکیب میشوند تا به بهترین راهحل دست یابیم.
بنابراین میتوانیم بگوییم که
- مسئله باید بتواند به مسائل فرعی همپوشان تقسیم شود.
- بتوان با استفاده از یک راهحل بهینه برای مسائل فرعی کوچکتر به راهحل بهینه دست پیدا کرد.
- الگوریتم دینامیک از بهخاطرسپاری (Memoization) استفاده میکند.
مقایسه
برخلاف الگوریتم حریصانه که در آن بهینهسازی موضعی بررسی میشد، در الگوریتمهای دینامیک تلاش میشود تا بهینهسازی کلی برای مسئله به دست آید.
برخلاف الگوریتمهای تقسیم و حل که راهحلها با هم ترکیب میشوند تا به یک راهحل نهایی دست پیدا کنیم، در الگوریتمهای دینامیک از خروجی برخی مسائل فرعی برای بهینهسازی مسائل فرعی دیگر استفاده میشود. الگوریتمهای دینامیک از بهخاطرسپاری برای به یاد آوردن خروجیهایی که قبلاً برای مسائل فرعی حل شده به دست آوردهاند بهره میگیرند.
مثال
در ادامه مسائل رایانهای که میتوان با استفاده از رویکرد برنامهنویسی دینامیک حل کرد ارائه شدهاند:
- سریهای عددی فیبوناچی (Fibonacci number series)
- مسئله کولهپشتی (Knapsack problem)
- برج هانوی (Tower of Hanoi)
- کوتاهترین مسیر بین همه زوج نقاط با الگوریتم فلوید-وارشال (All pair shortest path by Floyd-Warshall)
- کوتاهترین مسیر با دکسترا (Shortest path by Dijkstra)
- زمانبندی پروژه (Project scheduling)
در این نوشته تلاش کردیم تا الگوریتمهای مختلفی که هنگام کار با ساختارهای دادهای مورد استفاده قرار میگیرند را معرفی کنیم و در مورد هر یک مثالهایی معرفی کردیم.
اگر این نوشته مورد توجه شما قرار گرفته است، پیشنهاد میکنیم موارد زیر را نیز بررسی کنید:
- آموزش طراحی الگوریتم
- مجموعه آموزش های تئوری و عملی الگوریتم ژنتیک
- آموزش حل مسائل گسسته با استفاده از الگوریتم PSO
- آموزش روش حریصانه در طراحی الگوریتم
- مجموعه آموزش های الگوریتم ژنتیک و محاسبات تکاملی
- آموزش حل مسأله کوله پشتی با الگوریتم ژنتیک
==













سلام
متشکر از متن خوبتون