تنش استوانه ای (Cylinder Stress) — تاریخچه، روابط و کاربردها

«تنش استوانه‌ای» (Cylinder Stress)، نوعی توزیع تنش با تقارن چرخشی است. این نوع تنش در اجسام استوانه‌ای مشاهده می‌شود. در این حالت، اگر جسم حول یک محور ثابت دوران کند، هیچ تغییری در توزیع تنش رخ نخواهد داد.

تنش استوانه‌ای شامل سه الگوی زیر می‌شود:

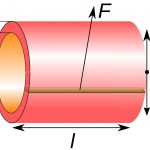
• «تنش حلقوی» (Hoop Stress) یا «تنش پیرامونی» (Circumferential Stress): نوعی تنش نرمال در جهت مماس بر نقطه مورد بررسی (تصویر زیر) است.
• «تنش محوری» (Axial Stress): نوعی تنش نرمال موازی با محور تقارن استوانه است.
• «تنش شعاعی» (Radial Stress): تنشی که با محور تقارن استوانه در یک صفحه قرار دارد اما بر آن محور عمود است.

یک مثال متداول و علت اصلی نام‌گذاری تنش حلقوی، نیروی کششی اعمال شده بر نوارهای فلزی یا حلقه‌های اطراف یک بشکه چوبی است (تصویر زیر). در یک لوله مستقیم، اعمال نیروی‌های ناشی از اختلاف فشار به دیواره لوله، باعث افزایش تنش‌های حلقوی می‌شوند. به طور مشابه، در صورتی که سرپوش دو انتهای لوله صاف باشد، نیروی اعمال شده ناشی از فشار استاتیک، یک تنش محوری عمود بر دیواره را ایجاد خواهد کرد. تنش شعاعی در مقاطع نازک، اغلب کوچک و قابل اغماض است. با این وجود، برای مدل‌سازی دقیق ورقه‌های استوانه‌ای با جدار ضخیم باید این‌گونه تنش را در محاسبات مد نظر قرار داد.

تاریخچه توسعه تحلیل تنش استوانه‌ای

اولین تحلیل تنش در اجسام استوانه‌ای توسط «ویلیام فیربرن» (William Fairbairn)، یکی از مهندسان عمران قرن 19 ام میلادی، با کمک «ایتن هاجکینسون» (Eaton Hodgkinson)، یکی از مهندسان پیشگام در زمینه به کارگیری تحلیل‌های ریاضی در طراحی سازه‌ها توسعه یافت.

فیلم آموزش مقاومت مصالح – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

مطالعات اولیه این محققین بر روی طراحی و ارزیابی شکست دیگ‌های بخار صورت گرفت. در طی این مطالعات، فیربرن متوجه شد که میزان تنش حلقوی دو برابر میزان تنش محوری (طولی) است و عامل مهمی در هنگام مونتاژ ورقه‌های دیگ بخار به حساب می‌آید. این ورقه‌ها با استفاده از اتصال (پرچ کردن) ورقه‌های نورد شده به یکدیگر ساخته می‌شوند.

مطالعات بعدی در این زمینه، برای ساخت پل‌ها و اختراع «شاه تیر جعبه‌ای» (Box Girder) مورد استفاده قرار گرفتند. در تصویر زیر، ستون‌های چدنی «پل چپستاو» (Chepstow Bridge) را مشاهده می‌کنید که توسط نوارهای بیرونی ساخته شده از آهنِ کار شده، تقویت شده‌اند. نیروی طولی و عمودی در این نوارها به صورت فشاری است و چدن قابلیت مقاومت در برابر این‌گونه نیرو را دارد. از طرف دیگر، به دلیل مقاومت بیشتر آهنِ کار شده در برابر تنش حلقوی (نسبت به چدن)، این ماده نیز در اطراف ستون مورد استفاده قرار گرفته است.

تنش حلقوی

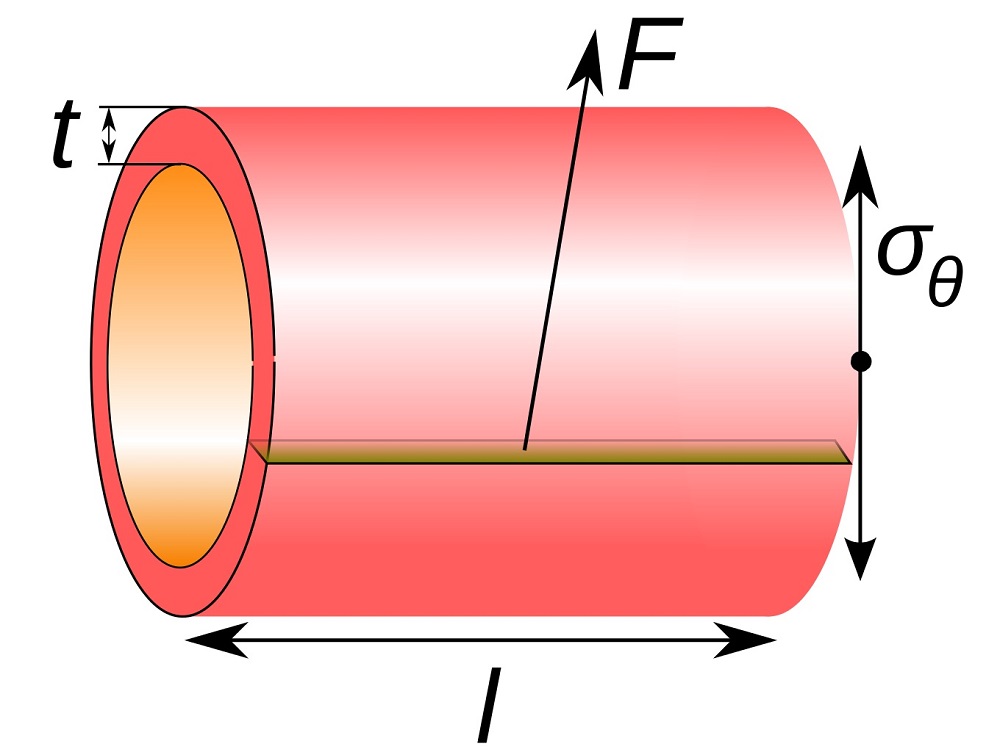
تنش حلقوی، نیرویی است که به صورت محیطی (عمود بر راستای محور و شعاع جسم) به تمامی ذرات دیواره استوانه اعمال می‌شود.

فیلم آموزش مقاومت مصالح – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

این تنش را می‌توان از طریق رابطه زیر بیان کرد:

F: نیروی محیطی اعمال شده بر سطح دیواره استوانه؛ t: ضخامت شعاعی استوانه؛ l: طول محوری استوانه

یکی از کمیت‌های جایگزین تنش حلقوی برای توصیف تنش محیطی، «تنش دیواره» (Wall Stress) یا «کشش دیواره» (Wall Tension) نام دارد. این کمیت به صورت نیروی محیطی در امتداد کل ضخامت شعاعی (طول استوانه) تعریف می‌شود.

T: تنش دیواره؛ F: نیروی محیطی؛ l: طول استوانه

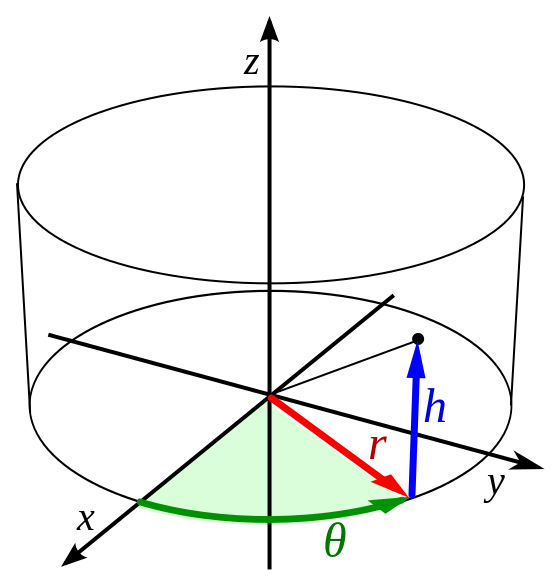
تنش‌های محوری و شعاعی به همراه تنش محیطی، مؤلفه‌های تانسور تنش در مختصات استوانه‌ای را نمایش می‌دهند (تصویر زیر). برای اجسام دارای تقارن چرخشی، تجزیه نیروهای اعمال شده به مؤلفه‌های موازی با مختصات استوانه‌ای z ،r و θ به انجام بهتر محاسبات کمک می‌کند. این مؤلفه‌های نیرو به ترتیب باعث به ایجاد تنش‌های شعاعی، محوری و حلقوی می‌شوند.

رابطه بین فشار داخلی و تنش استوانه‌ای

اجسام استوانه‌ای شکل با توجه به نسبت شعاع به ضخامت دیواره‌شان، به دو گروه «جدار نازک» (Thin-walled) و «جدار ضخیم» (Thick-walled) تقسیم می‌شوند. در ادامه به معرفی رابطه بین فشار داخلی و مولفه‌های تنش استوانه‌ای (تنش حلقوی، شعاعی و محوری) در این دو گروه می‌پردازیم.

استوانه جدار نازک

استوانه‌ای که نسبت شعاع به ضخامت دیواره آن بیشتر از 10 (نسبت قطر به ضخامت کمتر از 20) باشد، استوانه جدار نازک به حساب می‌آید. در این حالت می‌توان دیواره را به صورت یک سطح در نظر گرفت. به این ترتیب، تنش حلقوی ناشی از فشار داخلی بر روی یک استوانه نازک با استفاده از «معادله یانگ-لاپلاس» (Young–Laplace Equation) قابل محاسبه خواهد بود:

P: فشار داخلی؛ t: ضخامت دیواره؛ r: میانگین شعاع استوانه؛ σ_θ: تنش حلقوی

معادله تنش حلقوی در ورقه‌های نازک، برای پوسته‌های کروی نظیر سلول‌های گیاهی و باکتری‌ها نیز تقریباً معتبر است. برای به کارگیری اجسام استوانه‌ای نظیر لوله‌ها در مسائل مهندسی، رابطه تنش حلقوی بر اساس فشار بازنویسی می‌شود که به آن، «معادله بارلو» (Barlow's Formula) می‌گویند.

در سیستم SI، فشار با واحد پاسکال (Pa) و ضخامت نیز مانند شعاع با واحد متر (m) بیان می‌شود. این واحدها در سیستم بریتانیایی به ترتیب، پوند بر اینچ مربع (psi) و اینچ (in) هستند.

در هنگام بسته بودن دو انتهای یک استوانه، اعمال فشار داخلی بر روی آن‌ها باعث ایجاد نیرویی در امتداد محور استوانه می‌شود. مقدار این نیرو بر واحد سطح، با عنوان تنش محوری شناخته می‌شود و معمولاً مقدار آن از تنش حلقوی کمتر است.

این تنش را می‌توان از طریق رابطه زیر نیز تخمین زد:

در این شرایط، علاوه بر تنش محوری یک تنش شعاعی (σ_r) نیز به وجود می‌آید که مقدار آن از طریق رابطه زیر برای استوانه جدار نازک قابل محاسبه است:

استوانه جدار ضخیم

هنگامی که نسبت شعاع به ضخامت استوانه کمتر از 10 باشد (نسبت قطر به ضخامت کمتر از 20)، معادلات استوانه جدار نازک دیگر قابل استفاده نخواهند بود؛ چراکه در این حالت، مقدار تنش‌های بین سطوح داخلی و خارجی استوانه به صورت قابل توجهی تغییر می‌کند. به علاوه، تنش‌های برشی موجود مقاطع نیز قابل اغماض نیستند. این تنش و کرنش‌ها را می‌توان با استفاده از «معادلات لامه» (Lamé Equations) محاسبه کرد. این معادلات توسط «گابریل لامه» (Gabriel Lamé)، ریاضیدان فرانسوی توسعه داده شده است.

A و B: ثابت‌های ادغام (از طریق شرایط مرزی تعیین می‌شوند)؛ r: شعاع نقطه مورد بررسی (بر روی بخش داخلی یا بیرونی دیواره)

A و B با استفاده از بررسی شرایط مرزی به دست می‌آیند. به عنوان مثال، این شرایط برای یک استوانه جامد (ساده‌ترین حالت) به صورت زیر است:

• اگر R_i=0 باشد، B=0 خواهد بود. به این ترتیب، یک جسم استوانه‌ای جامد نمی‌توان دارای فشار داخلی باشد. بنابراین داریم: A=P₀.

تاثیر تنش‌های حلوقی در حوزه‌های مختلف

حال اجازه دهید مروری بر تاثیر تنش‌های حلقوی در حوزه‌های مختلف داشته باشیم.

فیلم آموزش مقاومت مصالح – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

مهندسی

در اجسام استوانه‌ای اگر هیچ‌گونه بارگذاری خارجی بر روی جسم اعمال نشود، شروع شکستگی توسط تنش حلقوی کنترل خواهد شد. تنش حلقوی در چنین وضعیتی بزرگ‌ترین تنش اصلی خواهد بود. توجه داشته باشید که در یک جسم حلقوی، کرنش کل در بخش داخلی و خارجی یکسان است اما به دلیل توزیع کرنش در شرایط مختلف، بیشترین تنش در بخش داخلی ظاهر می‌شود. از این‌رو، بررسی وضعیت ایجاد و رشد ترک‌های یک لوله را باید از بخش داخلی آن شروع کرد. به همین دلیل، برای ارزیابی لوله‌ها پس از حوادثی مانند زمین‌لرزه، یک دوربین را به داخل لوله ارسال می‌شود تا ترک‌های داخلی مورد بررسی قرار گیرند. تسلیم در اجسام استوانه‌ای توسط یک تنش معادل کنترل می‌شود. این تنش، ترکیبی از تنش حلقوی و طولی یا شعاعی (در صورت عدم وجود تنش طولی) است.

پزشکی

در آسیب‌شناسی یا اصطلاحاً «پاتولوژی» (Pathology) دیواره رگ‌ها یا مجاری دستگاه گوارشی، کشش دیواره‌ها بیانگر کشش ماهیچه‌های دیواره رگ‌ها است. با توجه به «قانون لاپلاس» (Law of Laplace)، اگر دیواره رگ‌های خونی دچار عارضه «آنوریسم» (Aneurysm) (بیرون‌زدگی و بزرگ شدن دیواره) شوند، شعاع رگ افزایش می‌یابد. به این ترتیب، بر اثر کاهش نیروهای رو به داخل رگ، آنوریسم تا هنگام گسیختگی دیواره‌ها ادامه خواهد یافت. تمام این فرآیندها برای عارضه «دیورتیکول» (Diverticuli) در روده نیز صادق هستند. بررسی نحوه عملکرد این مشکلات با استفاده از مفهوم تنش حلقوی صورت می‌گیرد.

امیدواریم این مقاله برایتان مفید واقع شده باشد. اگر به یادگیری موضوعات مشابه علاقه‌مند هستید، آموزش‌های زیر را به شما پیشنهاد می‌کنیم:

• مجموعه آموزش های مهندسی عمران
• مجموعه آموزش‌های دروس مهندسی مکانیک
• نرخ کرنش — آشنایی با خصوصیات رفتاری مواد
• آموزش مقاومت مصالح
• مجموعه مقالات آشنایی با مفاهیم مقاومت مصالح و خواص مکانیکی مواد

^^