منطق شرطی (Conditional Logic) در جاوا اسکریپت – از صفر تا صد
این که برنامه نویسان با ریاضیات نیز آشنا باشند یک امتیاز محسوب میشود. البته آمار و احتمال یا حسابان نقش چندانی در کدنویسی ندارند؛ اما داشتن درک کلی از منطق بولی میتواند در این زمینه کمک بزرگی باشد. برای مثال کسانی که درک ریاضیاتی مناسبی دارند میتوانند عبارتهای شرطی پیچیده برنامهنویسی را به معادلهای بسیار سادهتری تبدیل کنند. در این نوشته به بررسی جامع عبارتهای شرطی زبان جاوا اسکریپت میپردازیم.

مقادیر درست و نادرست در جاوا اسکریپت
پیش از بررسی عبارتهای منطقی ابتدا به مفهوم «درستی» در جاوا اسکریپت میپردازیم. از آنجا که جاوا اسکریپت در مورد انواع داده سختگیری زیادی ندارد، در عبارتهای منطقی مانند عبارتهای if، && و || پاسخهای بولی ارائه میدهد و شروط سهتایی نیز همگی به مقادیر بولی منتهی میشوند. توجه داشته باشید که این بدان معنی نیست که همه عملیاتها در جاوا اسکریپت مقدار بولی باز میگردانند.
تنها شش مقدار نادرست در جاوا اسکریپت وجود دارد: false، null، undefiend، NaN، 0 و “” و هر چیزی جز اینها درست محسوب میشود. این بدان معنی است که [] و {} هر دو مقدار درستی هستند؛ هر چند شاید عجیب به نظر برسد.
عملگرهای منطقی
در منطق صوری تنها چند عملگر وجود دارند: نفی، عطف، فصل، استلزام و دوشرطی. هر کدام از اینها یک معادل جاوا اسکریپت دارند که به ترتیب !، &&، ||، if (/* شرط */) { /* آنگاه نتیجه */} و === هستند. این عملگرها همه دیگر عبارتهای منطقی را میسازند.
جدولهای درستی
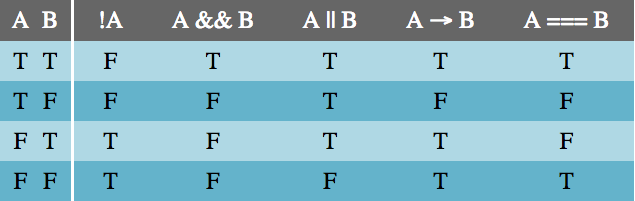
ابتدا به بررسی جدولهای درستی برای هر یک از عملگرهای پایه میپردازیم. یک جدول درستی، صدق یک عبارت را بر مبنای صدق اجزایش مشخص میسازد. جدولهای درستی بسیار مهم هستند. اگر دو عبارت، جدول درستی یکسانی ایجاد کنند در این صورت آن عبارتها معادل هم هستند و میتوانند به جای هم استفاده شوند.
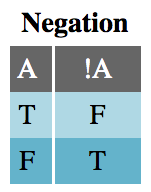
جدول نفی
جدول نفی کاملاً سرراست است. نفی تنها عملگر منطقی یگانه است که تنها روی یک ورودی عمل میکند. این بدان معنی است که A || B! همان (A || B)! نیست، چون پرانتز باعث میشوند که کل عبارت داخل آن نفی شود.
برای نمونه ردیف نخست جدول درستی نفی در زیر باید به صورت زیر خوانده شود: اگر عبارت A درست باشد، در این صورت عبارت A! نادرست است.
نفی یک عبارت ساده است و هیچ دشواری ندارد. منفی «هوا بارانی است»، عبارت «هوا بارانی نیست» خواهد بود و منفی مقدار ابتدایی true در جاوا اسکریپت به طور بدیهی مقدار false است. با این وجود عبارتهای منفی پیچیده هستند یا دست کم عبارتهایی هستند که چندان ساده به حساب نمیآیند. منفی عبارت «همواره باران میآید» چیست؟ یا منفی عبارت isFoo && isBar چه میتواند باشد؟
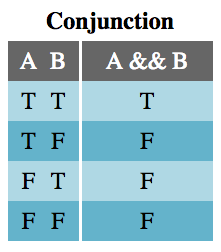
جدول عطف
جدول عطف نشان میدهد که عبارت A && B تنها در صورتی درست است که هر دو A و B درست باشند. این نکته برای کسانی که با جاوا اسکریپت کدنویسی میکنند، کاملاً آشنا است.
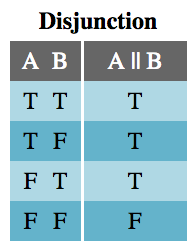
جدول فصل
جدول فصل نیز کاملاً آشنا است. یک عملیات فصل (OR منطقی) زمانی درست است که یا هر دو A و B درست باشند یا یکی از آن دو درست باشد.
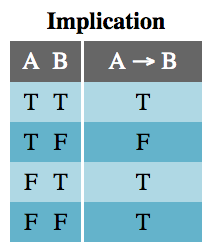
جدول استلزام
جدول استلزام شاید چندان آشنا نباشد. A استلزام میکند B را، یعنی درست بودن A به معنی درست بودن B است. با این حال B میتواند به دلیلی به جز درست بودن A نیز درست باشد. به همین دلیل دو ردیف آخر جدول درست هستند. تنها حالتی که استلزام منجر به نادرست بودن عبارت متأخر میشود، این است که A درست بوده و B نادرست باشد یعنی A، B را استلزام نمیکند.
با این که عبارت if در جاوا اسکریپت برای استلزام استفاده میشود؛ اما همه عبارتهای if بدین ترتیب عمل نمیکنند. معمولاً ما از if برای کنترل گردش برنامه استفاده میکنیم و نه بررسی درست بودن، چون توالی نیز در درست بودن مهم است. در ادامه یک عبارت کاملاً بدیهی برای if در معنی استلزام ارائه شده است:
function implication(A, B) {
if (A) {
return B;
} else {
/* if A is false, the implication is true */
return true;
}
}
اگر این عبارت تا حدودی بدشکل است، نگران نباشید. روشهای سادهتری نیز برای کدنویسی استلزام وجود دارند. به دلیل همین بدشکل بودن در ادامه از → به عنوان نماد استلزام در سراسر مقاله استفاده میکنیم.
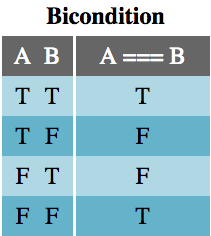
جدول دوشرطی
عملگر دو شرطی که برخی اوقات اگر و تنها اگر (IIF) نیز نامیده میشود، زمانی منجر به نتیجه درست میشود که هر دو عملوند A و B مقدار درستی یکسانی داشته باشند. به دلیل شیوه مدیریت مقایسهها در جاوا اسکریپت، استفاده از === به منظور منطقی تنها زمانی صورت میگیرد که عملوندها به صورت بولی درآیند. یعنی به جای A === B باید از A===!!B!! استفاده کنیم.
...
هشدار
هنگام استفاده از کد جاوا اسکریپت به مثابه منطق گزارهای، دو هشدار مهم وجود دارند که باید جدی گرفته شوند: اتصال کوتاه و ترتیب عملگرها
اتصال کوتاه
منظور از اتصال کوتاه چیزی است که موتورهای جاوا اسکریپت برای صرفهجویی در زمان انجام میدهند. مثلاً چیزهایی که خروجی کل یک عبارت را تغییر نمیدهند کلاً ارزیابی نمیشوند. برای نمونه تابع ()doSomething در مثال زیر هرگز فراخوانی نمیشود، زیرا مهم نیست که چه مقدار بازگشتی دارد، چون در هر حال خروجی عبارت منطقی تغییری نمییابد:
// doSomething() is never called false && doSomething(); true || doSomething();
به خاطر بیاورید که عطف (&&) زمانی درست است که هر دو عبارت درست باشند و فصل (||) نادرست است، تنها اگر یک طرف نادرست باشد. در هر یک از این حالتها پس از خواندن مقدار اول دیگر نیازی به خواندن مقدار دوم وجود ندارد، چون خروجی منطقی عبارت مشخص است.
به دلیل همین ویژگی جاوا اسکریپت گاهی اوقات قواعد جابجایی منطقی را نقض میکند.
از نظر منطقی A && B معادل B && A است؛ اما اگر عبارت window && window.mightNotExist را با عبارت window.mightNotExist && window جا به جا کنید، ممکن است برنامهتان از کار بیفتد. این بدان معنی نیست که در درست بودن یک عبارت جابجا شده تفاوتی ایجاد میشود؛ اما جاوا اسکریپت ممکن است خطایی هنگام تلاش برای تحلیل این عبارت ایجاد کند.
ترتیب عملیات
ترتیب عملیاتها در جاوا اسکریپت ممکن است برخی برنامه نویسان مبتدی را شگفتزده کند، زیرا در منطق صوری به جز گروهبندی و ترتیب چپ به راست، چیز دیگری به نام ترتیب وجود ندارد. مشخص شده است که بسیاری از زبانهای برنامهنویسی به && اولویت بالاتری نسبت به || میدهند. این بدان معنی است که && در ترتیب چپ به راست ابتدا گروهبندی میشود و سپس || در ترتیب چپ به راست گروهبندی میشود. یعنی A || B && C به همان ترتیب (A || B) && C ارزیابی نمیشود؛ بلکه به صورت A || (B && C) محاسبه میشود.
true || false && false; // evaluates to true (true || false) && false; // evaluates to false
خوشبختانه گروهبندی یعنی استفاده از پرانتز همچنان بالاترین اولویت را در جاوا اسکریپت دارد. با بهرهگیری از عبارتهای گسسته میتوان از ابهام و شگفتزدگی در هنگام محاسبه عبارتها جلوگیری کرد. به همین دلیل است که بسیاری از IDE ها اجازه نمیدهند در یک گروه از && و || بیش از حد استفاده کنید.
محاسبه جدولهای درستی ترکیبی
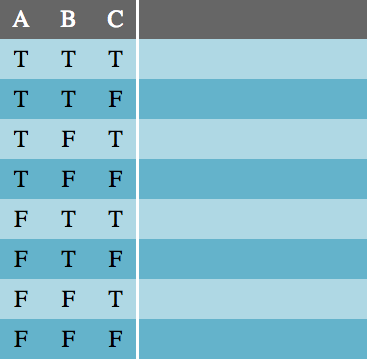
اینک که درستی عبارت ساده مشخص شد، درستی عبارتهای پیچیدهتر را نیز میتوان محاسبه کرد. برای شروع تعداد متغیرهای موجود در عبارت را میشماریم و یک جدول درستی مینویسیم که 2ⁿ ردیف داشته باشد. سپس یک ستون برای هر یک از متغیرها تشکیل میدهیم و این ستون را با همه ترکیبهای ممکن مقادیر درست/نادرست پر میکنیم. پیشنهاد میشود که نیمه ابتدایی ستون با مقادیر درست (T) و نیمه دوم با مقادیر نادرست (F) پر شود، سپس ستون بعدی پر شود و همین طور تا آخر.
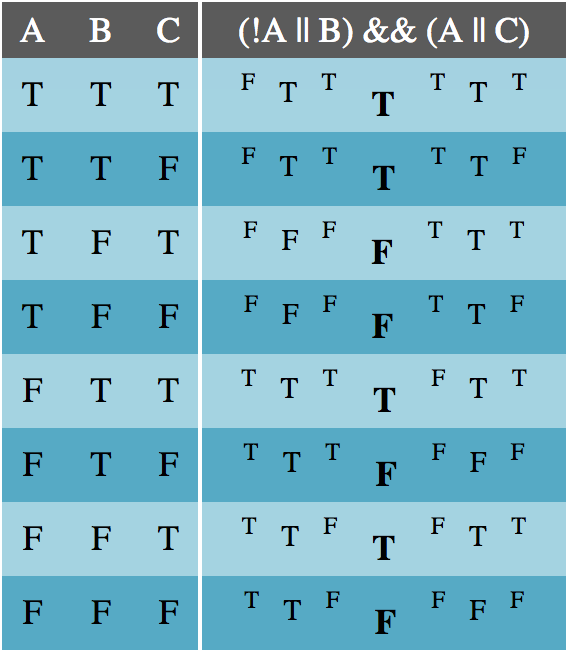
سپس عبارت را بنویسید و آن را در لایههای مختلف از درونیترین گروهها به سمت بیرون حل کنید و درستی هر بخش را تعیین کنید.
همان طور که در تصویر فوق مشخص است عبارتی که جدول درستی یکسانی تولید میکند میتواند به جای عبارت مفروض جایگزین شود.
قواعد جایگزینی
در ادامه چند نمونه از قواعد جایگزینی را که استفاده بیشتری دارند، مطرح خواهیم کرد. در این بخش هیچ جدول درستی ارائه نشده است؛ اما شما میتوانید آنها را خودتان تشکیل دهید تا درستی این قواعد را بررسی کنید.
نفی مضاعف
از نظر منطقی A و A!! معادل هم هستند. شما میتوانید در همه موارد علامت نفی مضاعف را حذف کنید و یا نفی مضاعف را به یک عبارت اضافه کنید و هیچ تغییری در درستی آن ایجاد نشود. اضافه کردن یک نفی مضاعف زمانی کارآمد است که بخواهیم بخش منفی یک عبارت پیچیده را محاسبه کنیم. یکی از معایب این روش آن است که در جاوا اسکریپت از !! برای تبدیل یک مقدار به معادل بولی نیز استفاده میشود، که میتواند تأثیر جانبی ناخواستهای ایجاد کند.
A ===!!A
جابجایی
در هر عملگر فصل (||)، عطف (&&) یا دوشرطی (===) میتوان ترتیب عملوندها را تغییر داد. جفتهای زیر از نظر منطقی معادل هم هستند؛ اما ممکن است به دلیل ایجاد اتصال کوتاه، در محاسبات برنامه تغییراتی ایجاد کنند.
(A || B) === (B || A) (A && B) === (B && A) (A === B) === (B === A)
شرکتپذیری
عملیاتهای فصل و عطف عملیاتهایی دودویی هستند، یعنی تنها روی دو ورودی عمل میکنند. با این که میتوان آنها را در زنجیرههای طولانیتری مانند A || B || C || D نیز کدنویسی کرد؛ اما آنها از چپ به راست به هم وابسته هستند یعنی ((A || B) || C) || D. قاعده شرکتپذیری بیان میکند که ترتیبی که این گروهبندی انجام مییابد، تأثیری بر خروجی منطقی عبارت نخواهد داشت.
((A || B) || C) === (A || (B || C)) ((A && B) && C) === (A && (B && C))
توزیع
شرکتپذیری در مورد هر دو ترکیب فصلی و عطفی صادق نیست. یعنی (A && (B || C))==! ((A && B) || C). برای این که در عبارت قبلی B و C را از هم جدا کنیم، باید ترکیب عطفی را توزیع کنیم، یعنی (A && B) || (A && C). این فرایند به طور معکوس نیز عمل میکند. اگر یک عبارت ترکیبی یا یک ترکیب عطفی یا فصلی وجود داشته باشد میتوان آن را از حالت توزیع یافته خارج ساخت که فرایندی شبیه فاکتورگیری از یک عبارت جبری است:
(A && (B || C)) === ((A && B) || (A && C)) (A || (B && C)) === ((A || B) && (A || C))
رخداد رایج دیگر توزیع به صورت توزیع مضاعف است که شبیه FOIL در جبر است:
1. ((A || B) && (C || D)) === ((A || B) && C) || ((A || B) && D)
2. ((A || B) && C) || ((A || B) && D) ===((A && C) || B && C)) || ((A && D) || (B && D))
(A || B) && (C || D) === (A && C) || (B && C) || (A && D) || (B && D) (A && B) ||(C && D) === (A || C) && (B || C) && (A || D) && (B || D)
استلزام مادی (Material Implication)
عبارتهای استلزامی (A → B) معمولاً به صورت { if (A) { B به زبان کد ترجمه میشوند، اما مواردی که یک عبارت ترکیبی چند استلزام در خود داشته باشد، بسیار مفید خواهد بود. بدین ترتیب یک عبارت if تو در تو خواهیم داشت. اما به جای آن میتوان از قاعده استلزام منطقی جایگزینی استفاده کرد که میگوید A → B یعنی A نادرست یا B درست است.
(A → B) === (!A || B)
گزاره همیشه صادق (Tautology) و تناقض (Contradiction)
گاهی اوقات در طی دستکاری عبارتهای منطقی ترکیبی به نتیجهای به صورت یک عبارت عطفی یا فصلی ساده میرسیم که تنها یک متغیر و نفی آن یا معادل بولیاش را دارد. در چنین مواردی این عبارت همواره یا درست (گزاره همیشه صادق) است یا همواره نادرست است (تناقض) و آن را در زمان کدنویسی میتوان با عبارت بولی معادلش جایگزین کرد:
(A ||!A) === true (A || true) === true (A &&!A) === false (A && false) === false
در همین ارتباط ترکیبهای فصلی و عطفی نیز وجود دارند که معادلهای بولی دیگری دارند. آنها را نیز میتوان صرفاً با درستی یک متغیر نمایش داد:
(A || false) === A (A && true) === A
ترانهش (عکس نقیض)
زمانی که افراد با یک استلزام مانند (A → B) سر و کار دارند، یکی از خطاهای رایج این است که فرض میکنند نفی بخش نخست یعنی A استلزام میکند که بخش دوم B نیز نفی شود یعنی A →!B!. این حالت معکوس استلزام است و لزوماً صادق نیست. یعنی برقرار بودن استلزام اولیه به این معنی نیست که معکوس آن نیز همواره صادق است، زیرا A یک شرط لازم برای B محسوب نمیشود. به عبارت دیگر اگر معکوس استلزام همواره (به دلایل مستقل) صحیح باشد در این صورت A و B دو شرطی هستند.
با این حال چیزی که از استلزام اولیه درمییابیم این است که عکس نقیض صحیح است. از آنجا که B یک شرط لازم برای A است، میتوان ادعا کرد که B →!A! یعنی:
(A → B) === (!B →!A)
هم ارزی مادی
نام عبارت دوشرطی از این واقعیت ناشی میشود که نیازمند دو عبارت شرطی (استلزام) است: A === B یعنی A → B و B → A. درستی مقادیر A و B به هم دیگر وابسته است. این نخستین قاعده هم ارزی مادی را به دست میدهد:
(A === B) === ((A → B) && (B → A))
با استفاده از استلزام مادی، نفی مضاعف، تناقض و جابهجایی میتوانیم این عبارت جدید را به چیزی تبدیل کنیم که کدنویسی آسانتری داشته باشد:
1. ((A → B) && (B → A)) === ((!A || B) && (!B || A))
2. ((!A || B) && (!B || A)) ===((!A &&!B) || (B &&!B)) || ((!A && A) || (B && A))
3. ((!A &&!B) || (B &&!B)) || ((!A && A) || (B && A)) ===((!A &&!B) || (B && A))
4. ((!A &&!B) || (B && A)) === ((A && B) || (!A &&!B))
(A === B) === ((A && B) || (!A &&!B))
صدور یا واگردان (Exportation)
عبارتهای if تودرتو و به طور خاص بخشهایی که واجد else نیستند، دارای ماهیتی کدنویسی هستند. یک عبارت if تودرتو ساده را میتوان به چیزی تبدیل کرد که یک شرط، ترکیب عطفی دو شرط قبلی خودش باشد:
if (A) {
if (B) {
C
}
}
// is equivalent to
if (A && B) {
C
}
(A → (B → C)) === ((A && B) → C)
قواعد دمورگان (DeMorgan)
قواعد دمورگان برای کار با عبارتهای منطقی ضروری هستند. این قواعد شیوه توزیع یک نفی روی ترکیبهای عطفی و فصلی را مشخص میسازند. عبارت (A || B)! را در نظر بگیرید. قاعده دمورگان تعیین میکند که وقتی یک ترکیب عطفی (یا فصلی) نفی میشود؛ باید هر عبارت مستقلاً نفی شود و سپس عطف (یا فصل) به فصل (یا عطف) تبدیل شود. از این رو (A || B)! همان A && !B! است. به طور مشابه (A && B)! با A || !B! همارز است.
!(A || B) ===!A &&!B !(A && B) ===!A ||!B
سهتایی (If-Then-Else)
عبارتهای سهتایی (A? B: C) موارد استفاده زیادی در برنامهنویسی دارند؛ اما دقیقاً به معنی استلزام نیستند. ترجمه یک سهتایی به زبان منطق صوری در واقع عطف دو استلزام است، یعنی A → B و A → C! که میتوان آن را با استفاده از استلزام مادی به صورت زیر نوشت:
(A? B: C) === (!A || B) && (A || C)
XOR (یای انحصاری)
یای انحصاری که غالباً به صورت XOR نوشته میشود، یعنی «یا این، یا آن؛ و نه هر دو». این عملگر از یای معمولی متفاوت است، زیرا در این مورد هر دو عبارت همزمان نمیتوانند درست باشند. درواقع هنگام استفاده از عبارت «یا» در زبان روزمره نیز در اغلب موارد منظور ما همین یای انحصاری است. جاوا اسکریپت عملگر درونی xor ندارد و از این رو به صورت زیر آن را استفاده میکنیم:
A یا B، اما نه هر دوی A و B
(A || B) && !(A && B) ترجمه مستقیم
(A || B) && (!A || !B) قواعد دمورگان
(!A || !B) && (A || B) جابجایی
A ? !B : B if-then-else تعریف
A ? !B : B معادل یای انحصاری (XOR) در جاوا اسکریپت است.
به طور جایگزین
A یا B، اما نه هر دوی A و B
(A || B) && !(A && B) ترجمه مستقیم
(A || B) && (!A || !B) قواعد دمورگان
(A && !A) || (A && !B) || (B && !A) || (B && !B) توزیع مضاعف
(A && !B) || (B && !A) جایگزینی تناقض
A === !B یا A !== Bهم ارزی مادی
A ===!B یا A!== B همان XOR در جاوا اسکریپت است.

منطق مجموعهها
تا به اینجا عبارتهایی را که شامل دو یا چند مقدار بودند بررسی کردیم؛ اما اینک توجه خود را به مجموعه مقادیر معطوف میکنیم. همانطور که عملگرهای منطقی در عبارتهای ترکیبی صدق خود را به روشی قابل پیشبینی حفظ میکنند، تابعهای محمولی روی مجموعهها نیز به همین روش صدق خود را حفظ میکنند.
منظور از یک تابع محمولی (predicate function) تابعی است که ورودی آن از یک مجموعه و خروجی آن یک مقدار بولی است. در نمونه کدهای زیر از آرایهای از اعداد برای یک مجموعه و دو تابع محمولی استفاده میکنیم:
isOdd = n => n% 2!== 0;
isEven = n => n% 2 === 0;
گزارههای عمومی
منظور از گزاره عمومی گزارهای است که روی همه عناصر یک مجموعه اعمال شود، یعنی تابع محمولی آن برای همه عناصر مقدار درست بازگرداند. اگر محمول برای هر یک از عناصر مجموعه مقدار نادرست بازگرداند در این صوت گزاره عمومی نادرست است. Array.prototype.every یک تابع محمولی انتخاب میکند و تنها در صورتی مقدار درست باز میگرداند که همه عناصر آرایه برای آن محمول درست باشند. همچنین در صورتی که یک محمول نادرست باشد از همان جا مقدار نادرست باز میگرداند و دیگر همه عناصر را آرایه بررسی نمیکند. از این رو هنگام استفاده از محمولات باید از عوارض جانبی آن جلوگیری کنید.
به عنوان نمونه آرایه [2, 4, 6, 8] را در نظر بگیرید. گزاره عمومی «هر عنصر آرایه زوج است» را داریم. با استفاده از تابع isEven و تابع عمومی درونی جاوا اسکریپت میتوانیم مقایسه زیر را اجرا کنیم و دریابیم که این گزاره عمومی صحیح است:
[1, 3, 5].some(isEven)
Array.prototype.every یک گزاره عمومی در جاوا اسکریپت است.
گزارههای وجودی
یک گزاره وجودی در مورد یک مجموعه، ادعایی معین دارد، یعنی دست کم یک عنصر در آرایه هست که برای تابع محمولی مقدار درست باز میگرداند. اگر محمول برای همه عناصر مجموعه مقدار نادرست باز گرداند در این صوت گزاره وجودی نادرست است.
جاوا اسکریپت از گزارههای وجودی درونی نیز پشتیبانی میکند: Array.prototype.some. مشابه every در گزاره عمومی، در این مورد نیز some در صورتی که یک عنصر محمول آن را تأمین کند، همان لحظه مقدار درست را باز میگرداند. به عنوان نمونه:
[1, 3, 5].some(isOdd)
تنها یک بار محمول IsOdd را اجرا میکند و (با مشاهده فرد بودن مقدار 1) مقدار درست بازمیگرداند. اما
[1, 3, 5].some(isEven)
مقدار نادرست باز میگرداند.
Array.prototype.some گزاره وجودی جاوا اسکریپت است.
استلزام عمومی
زمانی که یک گزاره عمومی را روی یک مجموعه مثلاً روی (nums.every(isOdd بررسی میکنیم، وسوسه میشویم که یکی از عناصر مجموعه را انتخاب کنیم که محمول را تأمین کند. با این حال یک تله در این حالت وجود دارد: در منطق بولی یک گزاره عمومی درست استلزام نمیکند که مجموعه غیر تهی باشد. گزارههای عمومی در مورد مجموعههای تهی همواره درست هستند و از این رو اگر بخواهید یک عنصر از مجموعه برای تأمین شرط انتخاب کنید باید به جای آن از بررسی وجودی استفاده کنید. برای اثبات مسئله every(() => false).[] را اجرا کنید تا ببینید که مقدار درست باز میگرداند.
گزارههای عمومی در مورد مجموعههای تهی همواره درست هستند.
نفی گزارههای عمومی و وجودی
نفی این گزارهها میتواند شگفتانگیز باشد. نفی یک گزاره عمومی مانند (nums.every(isOdd همان (nums.every(isEven نیست بلکه به صورت (nums.some(isEven است. در واقع این یک گزاره وجودی است که محمول آن منفی است. به طور مشابه نفی یک گزاره وجودی یک گزاره عمومی با محمول منفی است.
!arr.every(el => fn(el)) === arr.some(el =>!fn(el))
!arr.some(el => fn(el)) === arr.every(el =>!fn(el))
تقاطع مجموعهها
دو مجموعه با توجه به عناصرشان تنها به چند روش مشخص میتوانند با هم ارتباط داشته باشند. این روابط را میتوان به سادگی با استفاده از نمودارهای ون (Venn) نمایش داد و در اغلب میتوان آنها را در کد با استفاده از ترکیب گزارههای عمومی و وجودی تعیین کرد.
اشتراک مجموعهها
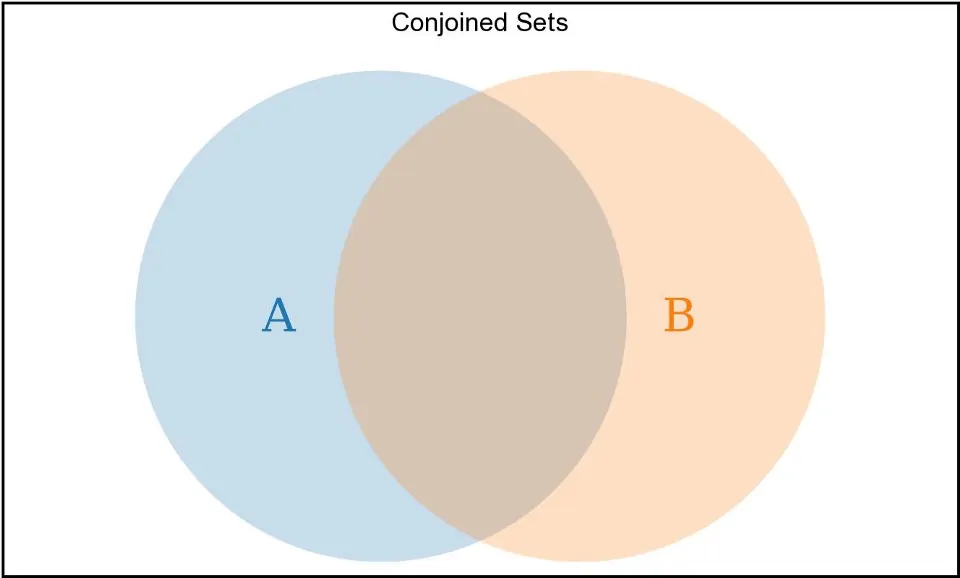
دو مجموعه میتوانند برخی از عناصر (و نه همه آنها) را به اشتراک بگذارند. در زیر نمودار ون نوعی دو مجموعه به هم چسبیده را میبینید:
A.some(el => B.includes(el)) && A.some(el =>!B.includes(el)) && B.some(el =>!A.includes(el))
یک جفت مجموعه به هم چسبیده را توصیف میکند.
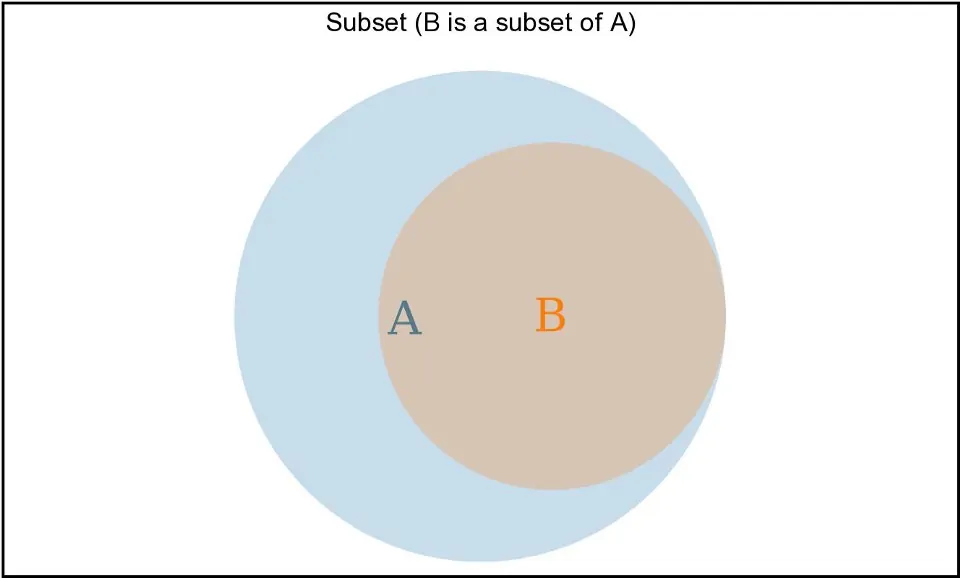
زیرمجموعهها
یک مجموعه میتواند شامل همه عناصر مجموعه دیگر باشد، اما عناصری داشته باشد که مجموعه دوم ندارد. این رابطه زیرمجموعه است و با Subset ⊆ Superset نشان داده میشود.
B.every(el => A.includes(el))
رابطه زیرمجموعه B ⊆ A را توصیف میکند.
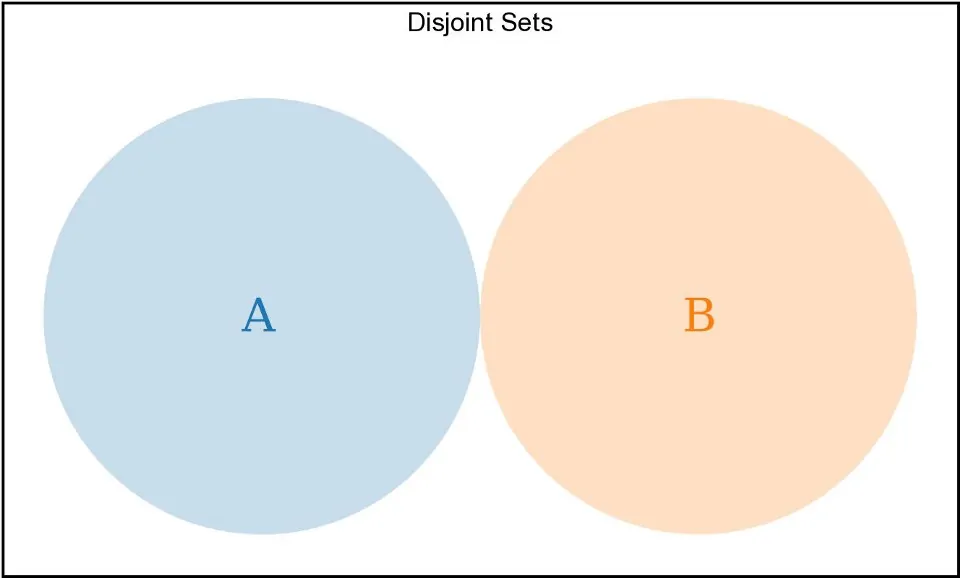
مجموعههای جدا از هم
دو مجموعه میتوانند هیچ عنصر مشترکی نداشته باشند. این دو مجموعه جدا از هم نامیده میشوند.
A.every(el =>!B.includes(el))
یک جفت مجموعه جدا از هم را توصیف میکند.
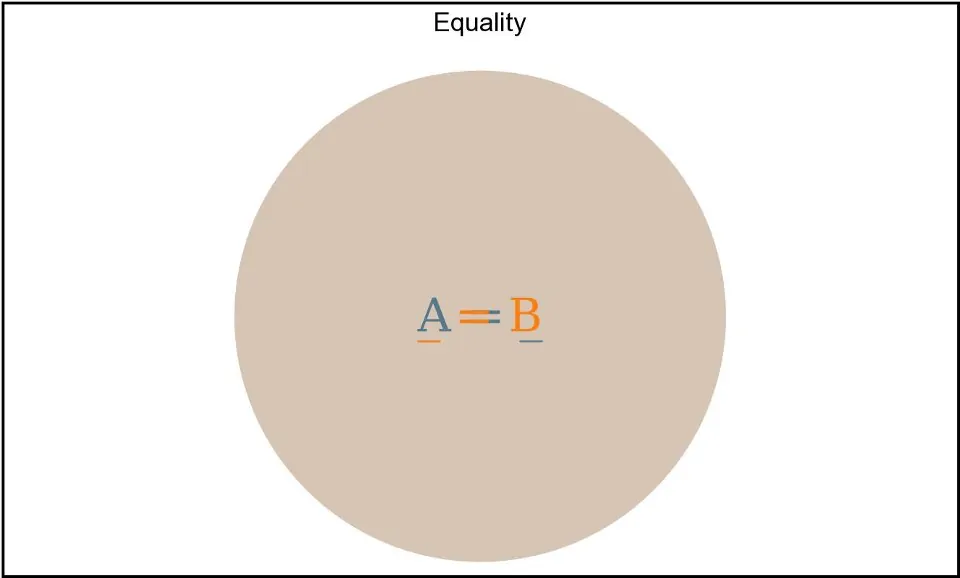
مجموعههای هم ارز
در نهایت دو مجموعه میتوانند همه عناصرشان مشترک باشد. یعنی زیرمجموعه همدیگر باشند. این مجموعهها مساوی هستند. در منطق صوری میتوان نوشت A ⊆ B && B ⊆ A ⟷ A === B اما در جاوا اسکریپت برخی موارد نقض برای آن وجود دارد. در جاوا اسکریپت یک Array در واقع یک مجموعه مرتب است و میتواند شامل مقادیر تکراری باشد و از این رو نمیتوان فرض کرد که کد زیرمجموعه دو شرطی B.every(el => A.includes(el)) && A.every(el => B.includes(el)) استلزام میکند که آرایه A و B همارز باشند. اگر A و B دو مجموعه باشند (یعنی با ()new set ایجاد شده باشند)، در این صورت مقادیر آنها منحصر به فرد است و میتوانیم زیرمجموعه دو شرطی را بررسی کنیم تا ببینیم آیا A === یا نه.
(A === B) === (Array.from(A).every(el => Array.from(B).includes(el)) && Array.from(B).every(el => Array.from(A).includes(el))
به این شرط که A و B با استفاده از ()new set ایجاد شده باشند.
ترجمه زبان منطق به زبان محاوره
این بخش احتمالاً مفیدترین بخش این مقاله است. در این بخش اکنون که با عملگرهای منطقی، جدول درستی و قواعد جایگزینی آشنا شدید، میتوانید شیوه ترجمه عبارت محاوره به زبان کد و سادهسازی آن را بیاموزید. با یادگیری این مهارت، شما میتوانید کد را نیز بهتر بخوانید و منطقهای پیچیده را در ذهن خود به عبارتهای سادهتر تبدیل کنید.
در ادامه جدولی از کد منطقی (چپ) و معادلهای محاورهای (راست) آن ارائه شده است.
| با فرض این که A و B مقادیر درست یا نادرست باشند | با فرض این که X و Y آرایه باشند | ||||
| زبان منطق / کد | زبان محاوره | زبان منطق / کد | زبان محاوره | ||
| !A | نیستA |
X.every(x => Y.includes(x))
| همه عناصر X در Y هستند | ||
| موردی نیست که A باشد | هر عنصر X در Y است | ||||
| A && B | A و B | برای هر x در X می توان گقت x در Y است | |||
| A مگر B | هر عنصر X عنصر Y است | ||||
| A به جز B | تنها عناصر Y عناصر X هستند | ||||
| A الا B | هیچ چیز جز عناصر X در Y نیست | ||||
| A تاجایی که شامل B | تنها Xبرابر با Yاست | ||||
| A به غیرB | هیچ X نیست که Y نباشد | ||||
| هم A و هم B | هر چه در X است در Y نیز هست | ||||
| A بدون B |
X.every(x => !Y.includes(x))
| X و Y جدا هستند | |||
| A تا جایی که B | هیچ X در Y نیست | ||||
| A شامل B | هیچ یک از عناصر X در Y نیست | ||||
| A II B | A یا B | هیچ عنصر X و Y برابر نیست | |||
| یا A یا B |
X.some(x => Y.includes(x))
| برخی X ها در Y هستند | |||
| B به جز A |
دست کم یک عنصر X در Y هست
| ||||
| A → B | اگر A آنگاه B | برخی از X ها در Y هستند | |||
| A فقط اگر B | دست کم یکی از عناصر X در Y است | ||||
| B اگر A | X های زیادی در Y هستند | ||||
| B به شرط A | یک x هست که هم در X و هم در Y است | ||||
| B با این شرط که A | یک X هست که Y است | ||||
| به شرط A آنگاه B | چند X در Y هستند | ||||
| B در شرایطی که A | X های بی شماری در Y هستند | ||||
| درشرایطی که A انگاه B |
X.some(x => !Y.includes(x))
| برخی عناصر X و Y مشترک هستند | |||
| A ایجاب می کند B را |
دست کم یک X هست که در Y نیست
| ||||
| B استلزام منطقی A است | برخی عناصر X در Y نیستند | ||||
| A موجب می شود B | یک عنصر X در Y نیست | ||||
| B از سوی A ایجاب شده است | همه X ها در Y نیستند | ||||
| B شرط لازم برای A است | بسیاری از عناصر X در Y نیستند | ||||
| A شرط کافی برای B است | چندعنصر X در Y نیستند | ||||
| B در صورتی که A | همه عناصر Y با X برابر نیستند | ||||
| درصورتی که A آنگاه B | |||||
| A === B | A اگر و فقط اگر B | ||||
| A در حالتی که B | |||||
|
A شرط لازم و کافی برای B است
| |||||
| !A && !B | نه A و نه B | ||||
| !(A II B) | نه A نه B | ||||
در ادامه برخی نمونههای عملی تبدیل محاوره به کد و برعکس که با استفاده از قواعد جایگزینی سادهسازی شدهاند نیز ارائه شده است:
نمونه 1
اخیراً اتحادیه اروپا مقررات عمومی حافظت از دادهها (GDPR) را ابلاغ کرد. فرض کنید شما شرکتی دارید که میخواهید این مقررات را به کار بگیرید. شرکت شما یک سیاست خاص در مورد کوکیها دارد که به کاربر اجازه میدهد اولویتهای خود را در مورد آنها تعیین نمایند. بدین منظور پنجرهای برای کاربر باز میشود و ترجیح وی سؤال میشود. برای این که این مسئله تا حد امکان به روشی پیادهسازی شود که تمرکز مخاطب را بر هم نزند، شرایط زیر (به ترتیب اولویت) وجود دارند:
- اگر کاربر در اتحادیه اروپا نیست، صفحه اولویتهای GDPR را هرگز نمایش نده.
- اگر بر اساس نیازهای برنامهنویسی نیازمند نمایش پنجره باشیم (اگر عمل کاربر نیازمند مجوزهایی بالاتر از مقداری باشد که اکنون تعیین شده است)، پنجره را نمایش بده.
- اگر کاربر اجازه داده است بنر GDPR که مداخله کمتری دارد نمایش یابد، پنجره را نمایش نده.
- اگر کاربر هنوز ترجیحهای خود را تعیین نکرده است (یعنی در یک کوکی ذخیره نشده است) پنجره را نمایش بده.
کدنویسی مقدماتی
برای پیادهسازی الزامات فوق میتوان یک سری عبارتهای if نوشت که به طور مستقیم بر اساس این الزامات مدلسازی شدهاند:
const isGdprPreferencesModalOpen = ({
shouldModalBeOpen,
hasCookie,
hasGdprBanner,
needsPermissions
}) => {
if (!needsPermissions) {
return false;
}
if (shouldModalBeOpen) {
return true;
}
if (hasGdprBanner) {
return false;
}
if (!hasCookie) {
return true;
}
return false;
}
بهینهسازی کد
کد فوق عملکرد مناسبی دارد؛ اما بازگشت دادن عبارتهای بولی رویه کدنویسی خوبی نیست. بنابراین مراحل زیر طی میشوند:
/* change to a single return, if-else-if structure */
let result;
if (!needsPermissions) {
result = false;
} else if (shouldBeOpen) {
result = true;
} else if (hasBanner) {
result = false;
} else if (!hasCookie) {
result = true
} else {
result = false;
}
return result;
/* use the definition of ternary to convert to a single return */
return!needsPermissions? false: (shouldBeOpen? true: (hasBanner? false: (!hasCookie? true: false)))
/* convert from ternaries to conjunctions of disjunctions */
return (!!needsPermissions || false) && (!needsPermissions || ((!shouldBeOpen || true) && (shouldBeOpen || ((!hasBanner || false) && (hasBanner ||!hasCookie))))
/* simplify double-negations and conjunctions/disjunctions with boolean literals */
return needsPermissions && (!needsPermissions || ((!shouldBeOpen || true) && (shouldBeOpen || (!hasBanner && (hasBanner ||!hasCookie))))
/* DeMorgan's Laws */
return needsPermissions && (!needsPermissions || ((!shouldBeOpen || true) && (shouldBeOpen || ((!hasBanner && hasBanner) || (hasBanner &&!hasCookie))))
/* eliminate tautologies and contradictions, simplify */
return needsPermissions && (!needsPermissions || (shouldBeOpen || (hasBanner &&!hasCookie)))
/* DeMorgan's Laws */
return (needsPermissions &&!needsPermissions) || (needsPermissions && (shouldBeOpen || (hasBanner &&!hasCookie)))
/* eliminate contradiction, simplify */
return needsPermissions && (shouldBeOpen || (hasBanner &&!hasCookie))
کد نهایی
در نهایت به کدی میرسیم که بسیار مناسبتر است و خوانایی بهتری نیز دارد:
const isGdprPreferencesModalOpen = ({
needsPermissions,
shouldBeOpen,
hasBanner,
hasCookie,
}) => (
needsPermissions && (shouldBeOpen || (!hasBanner &&!hasCookie))
);
نمونه 2
به قطعه کد زیر توجه کنید. در این مورد نیز میتوان مقادیر بازگشتی عبارتهای بولی را حذف کرد و بدین ترتیب کد را بازسازی نمود.
const isButtonDisabled = (isRequestInFlight, state) => {
if (isRequestInFlight) {
return true;
}
if (enabledStates.includes(state)) {
return false;
}
return true;
};
کد مقدماتی
برخی اوقات میتوان مراحل زیر را به صورت ذهنی یا روی کاغذ طی کرد؛ اما در اغلب موارد بهتر است هر مرحله در ادامه کد نوشته شود و مرحله قبلی حذف شود:
// convert to if-else-if structure
let result;
if (isRequestInFlight) {
result = true;
} else if (enabledStates.includes(state)) {
result = false;
} else {
result = true;
}
return result;
// convert to ternary
return isRequestInFlight
? true
: enabledStates.includes(state)
? false
: true;
/* convert from ternary to conjunction of disjunctions */
return (!isRequestInFlight || true) && (isRequestInFlight || ((!enabledStates.includes(state) || false) && (enabledStates.includes(state) || true))
/* remove tautologies and contradictions, simplify */
return isRequestInFlight ||!enabledStates.includes(state)
بهینهسازی کد
در نهایت به کد زیر میرسیم:
const isButtonDisabled = (isRequestInFlight, state) => ( isRequestInFlight ||!enabledStates.includes(state) );
در این مثال از محاوره استفاده نکردیم و در هیچ مرحلهای برای دستکاری کد، آن را به زبان محاوره درنیاوردیم، اما اینک در نهایت میتوان آن را به سادگی به صورت زیر به زبان محاوره ترجمه کرد: «دکمه غیرفعال میشود اگر درخواست در حال بررسی باشد یا وضعیت آن در مجموعه وضعیتهای فعال وجود نداشته باشد». هر زمان کد خود را به زبان محاوره ترجمه کردید و معنی نداشت در این صورت باید کد خود را مجدداً بررسی کنید. این حالت به طور مکرر رخ میدهد.
نمونه 3
زمانی که یک فریمورک تست A/B نوشته میشود، معمولاً دو مجموعه اصلی آزمایشهای فعال و غیرفعال وجود دارد که هر یک به صورت جداگانه (هر یک فایل جداگانهای در یک پوشه) بررسی میشوند و نتایج در یکی از دو لیست و نه هر دوی آنها ثبت میشود. این بدان معنی است که مجموعههای فعال شده و غیرفعال شده از هم جدا هستند و مجموعه همه آزمایشها زیرمجموعهای از پیوستگی این دو مجموعه آزمایش است. دلیل این که مجموعه همه آزمایشها باید زیرمجموعهای از ترکیب دو لیست باشد این است که نباید هیچ آزمایشی باشد که خارج از دو لیست قرار داشته باشد.
const isDisjoint =!enabled.some(disabled.includes) && !disabled.some(enabled.includes); const isSubset = allExperiments.every( enabled.concat(disabled).includes ); assert(isDisjoint && isSubset);
سخن پایانی
امیدواریم این مقاله برای شما مفید بوده باشد. در انتها باید اشاره کرد که نه تنها مهارت ترجمه بین زبان کد و زبان محاوره مفید است، بلکه آشنایی با اصطلاحهای منطقی برای بررسی روابط مختلف (مانند ترکیب عطفی و استلزامها) و همچنین ابزارهایی برای ارزیابی آنها (مانند جدول درستی) در امر برنامهنویسی در هر زبانی و به طور خاص در زبان جاوا اسکریپت بسیار کارآمد خواهد بود.
اگر این مطلب برای شما کاربردی بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای مهندسی نرم افزار
- آموزش مبانی منطق و نظریه مجموعه ها
- مجموعه آموزشهای پروژه محور برنامهنویسی
- آموزش جاوا اسکریپت (JavaScript)
- مجموعه آموزشهای طراحی و برنامهنویسی وب
- ۱۰ کتابخانه و فریمورک جاوا اسکریپت که باید آنها را بشناسید
- مجموعه آموزشهای سیستمها و منطق فازی
- بهینهسازی کدهای جاوا اسکریپت در سال ۲۰۱۸
- منطق ترکیبی را به زبان ساده و با مجموعه مقالات فرادرس یاد بگیرید
==