تاریخچه محاسبات باینری – آیا کامپیوترها همیشه به همین شکل که می شناسیم بودهاند؟
اخیراً مقالهای در وبسایت بلومبرگ منتشر شده است که نویسنده آن استفان میهم (Stephen Mihm) اعلام کرده برخی از رایانههایی که در سرویس درآمدهای داخلی (زیرمجموعه وزارت خزانهداری) ایالات متحده مشغول کار هستند، بسیار قدیمی محسوب میشوند و هنوز از همان کدهایی استفاده میکنند که در دهه 1950 برای کاهش هزینههای حسابرسی طراحی شدهاند.


این خبر باعث شد که توجه عمومی به سمت این رایانهها جلب شود. برخی از این رایانههای mainframe از سیستم دهدهی و برخی دیگر از روش «2out of 5 code» استفاده میکنند. شاید برای شما نیز جالب باشد که رایانههایی وجود دارند که از سیستم دودویی (باینری) استفاده نمیکنند.
در واقع رایانهها همیشه مانند امروز متکی بر سیستم محاسبات دودویی نبودهاند و روزگاری بوده است که از مبنایی به جز 2 (روشن/خاموش) استفاده میکردهاند. در مسیر تکامل رایانهها، فناوریهای مختلفی بودهاند که هر یک آزموده شده و کنار گذاشته شدهاند. برخی از انواع رایانهها حتی پیش از ظهور علم الکترونیک ابداع شدهاند. در ادامه برخی از این فناوریها را بررسی کردهایم.
ممکن است تاکنون از خود پرسیده باشید که چرا رایانهها از سیستم دودویی استفاده میکنند؟ برای پاسخ به این سؤال باید ساختار گیت منطقی را بررسی کنیم. این گیت به عنوان یک جزء پایهای از هر مداری، عبارتهای بولی همچون AND، OR، NOT و ... را دریافت میکند که برای هر برنامهنویسی آشنا است و شکل فیزیکی را در خروجی ارائه میکند. چنین محاسبهای را میتوان به صورت زنجیرهای از واکنشها تصور کرد، یک گیت منطقی، خروجی خود را به ورودی گیت دیگر میدهد تا اینکه پالسهای ولتاژ که به صورت 1 ها و 0 ها نمایش مییابند، در وضعیت نهایی خود آرایش بیابند.
اما چه میشود اگر یک حالت سوم نیز وجود داشته باشد؟ 0 برای خاموش، 1 برای روشن و 2 برای ... خیلی روشن؟ ازنظر فنی ممکن است؛ اما پیادهسازی آن دشوار است. اغلب در مورد سیستم دودویی از وضعیت دوگانه روشن/خاموش صحبت میکنیم؛ اما در واقعیت «روشن» و «خاموش» طیفی از مقادیر قابل پذیرش را در هر دو سر طیف نمایش میدهد. ایجاد یک حالت سوم قابل پذیرش و پایدار دشوار است. در اتحاد شوروی یکی از رویکردها برای پیادهسازی این وضعیت، استفاده از دو لوله خلأ برای نمایش سه وضعیت مجزا بوده است (00، 01، 11)، اما در زمان استفاده از قطعات الکترونیکی عوامل زیادی وجود دارند که ممکن است موجب افزایش یا کاهش ولتاژ شوند و درنتیجه وضعیتهایی بسیار بیشتر از حالت روشن/خاموش پدید میآیند.
اما اگر از ولتاژ استفاده نکنیم چطور؟ اگر از رسانهای استفاده کنیم که تمایز بین وضعیتها به طور مشخصتری روشن شده باشد چطور؟ برای مثال میتوانیم گیتهای منطقی خود را از میلههای چوبی بسازیم.
ماشین محاسبه سهگانه توماس فاولر (Thomas Fowler) که در سال 1840 میلادی ساخته شد، یک نمونه از این دستگاهها بوده است. این ماشین مسائل ضرب و تقسیم را با استفاده از یک سری میلهها که بر روی یک سطح قرار داشتند انجام میداد. این میلهها میتوانستند به طور مستقیم در میانه صفحه قرار بگیرند (مقدار 0)، از یک طرف خارج شوند (مقدار 1+) و یا از طرف دیگر صفحه بیرون بیایند (1-). این ماشین با نمایش سه وضعیت مختلف میتوانست محاسبات را به خوبی نمایش داده و انجام دهد. در ویدیوی زیر طرز کار ماشین فاولر توضیح داده شده است:
این روش سهگانه متعادل نامیده میشود. برای توضیح روش عملکرد آن باید ابتدا به سیستم دودویی متعارف که همه میشناسیم ارجاع بدهیم. در این سیستم هر بیت نماینده افزایشی در مبنای 2 است و مقدار کلی عدد از جمع زدن همه بیتها حاصل میآید. برای مثال:

در اعداد سهسهیی هم همین وضعیت حاکم است به جز اینکه مقادیر منفی تفریق و مقادیر مثبت جمع میشوند. بدین ترتیب:
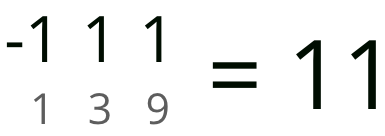
بیت اول 0^3 که همان 1 است، 1^3 برابر با 3 است. 2^3 همان 3*3 است که برابر با 9 خواهد بود. بنابراین 11 برابر است با 1-3+9. ممکن است متوجه شده باشید که با قرار دادن مقدار 1- در جدول نیاز به استفاده از بیت علامت برای تعیین اینکه عدد مثبت است یا منفی نیز از بین میرود.
اگر به دقت در مورد گنجاندن وضعیت سوم در این ترکیب فکر کنید، متوجه میشوید که در واقع دو روش مختلف برای انجام محاسبات سهسهیی وجود دارد. علاوه بر {1,0,1-} میتوانستید از {0,1,2} نیز استفاده کنید. این روش دوم به نام سهسهیی نامتعادل نامید میشود و در این روش عدد 11 به صورت 1-0-2 (1+1+9) نمایش مییابد. همچنین میتوان از کسرها نیز استفاده کرد: {1, 1/2, 0}.
عمل جمع نیز به همان روشی صوت میگیرد که در سیستم دودویی وجود دارد. یک جدول از مقادیر وجود دارد که مشخص میکند کدام ترکیبها از 0، 1 و 1- منجر به کدام اعداد میشوند و یک جدول انتقال وجود دارد. مزیت اصلی در این سیستم آن است که از نظر نمایی هر چه اعداد بزرگتر میشوند، بیتهای کمتری استفاده میشود و از این رو این فرایند بهینهتر است و از برق کمتری نیز استفاده میکند. در سوی دیگر تفریق به معنی NOT کردن عدد و سپس جمع کردن است. بنابراین بسیار بهتر از سیستم دودویی است. ضرب و تقسیم به مقدار زیادی راحتتر است، زیرا بیتهای کمتری برای هر عدد وجود دارند و از این رو مراحل آن کمتر است.
مدارهای سهسهیی بر اساس این مفاهیم پایه ساخته میشوند و به نوبه خود کاملاً جذاب هستند. اگر علاقهمند هستید در مورد ساخت گیتهای منطقی برای مدارهای سهسهیی بیشتر بدانید میتوانید از این مقالات استفاده کنید.
نقش رایانههای دودویی منفی در مبارزه با نازیها
زمانی که نازیها در سال 1939 لهستان را اشغال کردند، همه دانشگاهها تعطیل شدند. در این میان دانشگاه فناوری ورشو که نقشی شبیه به MIT در لهستان داشت نیز بینصیب نماند.
یان چوخرالسکی (Jan Czochralski) که تحقیقات وی بر روی مونوکریستال ها منجر به اختراع تراشههای سیلیکونی در طی یک دهه بعدتر شد، نازیها را با این استدلال که آنها میتوانند به امور جنگی کمک کنند، متقاعد کرد که اجازه دهند بخشهایی از دانشگاه مجدداً دایر شوند. بدین ترتیب آنها روزها بر روی مسائل مربوط به تعمیر و نگهداری تجهیزات نظامی ارتش آلمان کار میکردند و شبها برای نیروی مقاومت علیه نازیها تپانچه و تفنگ میساختند. تیم چوخرالسکی سلاحهای مورد استفاده ارتش ملی لهستان به خصوص مواد منفجره را تأمین میکردند. همزمان تیمی از اساتید دانشگاهی آسیبپذیریهای دستگاههای رادیویی و قطعات مختلف موشکهای V-2 آلمان را بررسی کرده و اطلاعات آنها را تحویل نیروی مقاومت میدادند.
در همین زمان بخش دیگری از دانشگاه که از سوی آلمانیها برای امور جنگی مفید تشخیص داده نشده بود، به صورت زیرزمینی مشغول کار بود. هزاران دانشجوی دانشگاه ورشو به صورت محرمانه دورههای آموزشی را میگذارند و نزدیک به 200 نفر از آنها در طی سالهای جنگ درجه مهندسی خود را دریافت کردند. 20 نامزد PhD رسالههای خود را به نگارش در آورده و در نهایت دفاع کردند.
پس از جنگ مبارزان مقاومت شروع به ثبتنام به عنوان دانشجو در دانشگاه بازگشایی شده نمودند. یاسک کارپینسکی (Jacek Karpiński) که در زمان ساخت بمبهای دستساز تقریباً به طور کامل بدن خود را از دست داده بود و در طی قیام ورشو از ناحیه ستون فقرات مورد اصابت گلوله قرار گرفته بود، در سال 1970 شروع به ساخت نخستین رایانه جهان (K-202) کرد. این رایانه پنج سال قبل از ساخت Altait 8800 در MIT بوده است. دههها طول کشید تا این صنعت بتواند رایانهای با چنان ظرفیت حافظه و عملکرد بسازد.
لئون ووکاشویچ (Leon Łukaszewicz) که در ارتش ملی لهستان به عنوان تکتیرانداز خدمت میکرد، شروع به طراحی چندین رایانه به نامهای ARR، XYZ و ZAM-2 نمود که در زمان خود در لبه این فناوری بود. وی همچنین تیمی از برنامه نویسان نابینا را سازماندهی و مدیریت کرد.
آندری تارکوفسکی (Andrzej Targowski) از اعدام جوخه آتش آلمانیها جان به در برد و در سن هفتسالگی از تودهای از اجساد مرده بیرون کشیده شد. وی در زمان بزرگسالی مفهوم INFOSTRADA را ارائه کرد (این پروژه به سرعت از سوی شوروی متوقف شد) INFOSTRADA همان اینترنتی است که امروز استفاده میکنیم.
این تیم اقدام به توسعه BINEG کرد که یک رایانه دودویی منفی (negabinary) بود.
در سیستم دودویی منفی، مبنا منفی است. بنابراین به جای 2⁰, 2¹, 2² اعداد به صورت 2⁰-, 2¹-, 2²- هستند. اگر با دقت این مقاله را مطالعه کرده باشید، احتمالاً با تأثیر عجیبی که این روش بر روی بیتها دارد آشنا شدید: ضرب کردن یک عدد منفی در یک عدد منفی، حاصلضربی مثبت تولید میکند. از این رو همه بیتهای زوج در سیستم دودویی منفی مثبت هستند.

در سیستم دودویی منفی نیز مانند سیستم سهسهیی مدیریت اعداد منفی آسانتر است، زیرا به بیت علامت نیازی نداریم. برخلاف روش سهسهیی درنهایت به بیتهای بیشتری برای نمایش اعداد نیاز داریم و این مقدار حتی از سیستم دودویی معمولی ساده نیز بیشتر است. جای شگفتی نیست که این ایده چندان مورد استقبال قرار نگرفته است.
2 از 3 تنها برای بازی سنگ-کاغذ-قیچی استفاده نمیشود
تا این جای نوشته بیشتر در مورد حالتهای مختلف مبنای اعداد بحث کردیم در ادامه به دستگاههایی میپردازیم که از مبنای 2 استفاده میکردهاند. اما روش استفاده آنها از سیستم دودویی بسیار متفاوت از رایانههای مدرن است.
در ابتدای نوشته اشاره شد که انگیزه این نوشته مشاهده برخی رایانههایی بوده است که در اداره درآمدهای داخلی ایالات متحده از سیستم «2 از 5» ( 2out of 5) استفاده میکنند.
روش محاسبات m از n که به نام کد وزن ثابت نیز نامیده میشود، مطابق نامش عمل میکند. در این رایانهها یک کلمه (word) باید دقیقاً m بیت داشته باشد تا 1 شود و بقیه بیتها باید 0 باشند. با اینکه این ایده ممکن است عجیب به نظر بیاید؛ اما در مورد رایانههای مین فریم بزرگ و بسیار قدیمی که دادهها به صورت ناپایداری ذخیره میشدند، کاملاً مناسب بوده است. با الزام اینکه m بیت در یک مجموعه برابر با 1 باشند در واقع یک روش بررسی خطا مورد استفاده قرار میگرفته است. این ماشین میبایست چندین بیت را به یکباره به روشی خاص تغییر میداد تا مشکلات دادهای موجب بروز خطا نشود.
کد وزن ثابت ازنظر فنی بر روی هر مبنایی برای سیستم اعداد میتواند مورد استفاده قرار گیرد؛ اما کد 2 از 5 به طور خاص برای ماشینهای دهدهی (پایه 10) مناسب است. اینک احتمالاً با خود فکر میکنید که اگر مبنای 3 نیازمند سه وضعیت متفاوت است و اجرای آن کار دشواری است، در این صورت ماشینهای دهدهی چگونه میتوانند ده وضعیت مختلف ممکن را با همان قطعات داشته باشند؟
پاسخ این است که رایانههای دهدهی چنین کاری نمیکنند. مهندسان این دستگاهها روشهای مختلفی برای انکودینگ مبنای 10 بر روی سختافزاری که ماهیت دودویی دارد ابداع نمودهاند. به همین دلیل نام این دستگاهها سیستمهای دهدهی کد شده به صورت دودویی (BCD) است. آنچه که در مورد ترکیب رایانههای «دهدهی با کد دودویی» و «کد 2 از 5» جالب به نظرمی رسد، این است که تنها با دو بیت نمیتوان اعداد 0 تا 9 را در سیستم دودویی نمایش داد.
برای مثال عدد 0 عدد سنتی سیستم دودویی است که هیچ بیت روشنی ندارد. عدد 7 به صورت 2⁰+2¹+2² (یا 4+2+1) سه بیت روشن دارد. بنابراین برای اینکه این سیستم کار کند باید مشخص کنید که هر بیت چه مقداری را نمایش میدهد (وزن آن چیست؟) از آنجا که روشهای مختلفی برای این کار وجود دارد، نسخههای مختلفی نیز از رایانههای کد 2 از 5 وجود دارند. برخی از آنها مقادیر 0، 1، 2، 3، 6 را به پنج بیت اختصاص میدهند که اعداد 1 تا 9 را به روشی معقول با دو بیت تولید میکنند و تنها برای 0 به عدد عجیب 01100 نیاز دارند.
نسخههای دیگر رایانههای «کد 2 از 5» آشناتر هستند، زیرا در بارکدها مورد استفاده قرار میگیرند. POSTNET (سیستم بارکد قدیمی اداره پست که تا چند سال پیش در ایالات متحده برای مسیریابی بستههای پستی استفاده میشد) از توالی 0، 1، 2، 4، 7 استفاده میکرد. بدین ترتیب راهحلی ابتکاری برای مسئله نمایش 0 با دو بیت وجود داشت: 00011 (7+4) که در روش دیگر به صورت 11 جمع زده میشد.
استفاده از سیستم دو-پنچپنجی
آیبیام با معرفی رایانه 650 خود در سال 1953 شروع به تولید انبوه رایانهها نمود. این دستگاه بر مبنای محاسبات دهدهی دو-پنجپنجی عمل میکرد. یعنی هر کلمه در این سیستم اعداد 0 تا 9 را مانند سیستم دهدهی نمایش میداد؛ اما بیتهای تشکیل دهنده هر کلمه به دو گروه دستهبندی میشد.
گروه نخست دو بیت داشتند، یکی برای نمایش 0 و دیگری برای نمایش 5. گروه دوم پنج بیت داشتند که برای نمایش اعداد 0 تا 4 استفاده میشد.
مقدار یک کلمه در سیستم دو-پنجپنجی با افزودن بیتهای موجود در گروه اول (0 یا 5) به بیت بخش دوم (0 تا 4) محاسبه میشد. در نتیجه وضعیتهای زیر وجود داشتند:
0:0, 0:1, 0:2, 0:3, 0:4, 5:0, 5:1, 5:2, 5:3, 5:4
در این روش نیز همانند کد 2 از 5 خطاها به طور خودکار با الزام دو بیت روشن برای همه مقادیر صحیح بررسی میشد.
اگر بررسی خطا چندان حائز اهمیت نباشد، میتوانید بیت دوم را در سمت دوم سیستم دو-پنج پنجی نادیده بگیرید. رایانههای UNIVAC 60 و UNIVAC 120 رمینگتون به همین ترتیب عمل میکردند و همچنین وزن طرف دیگر را چنان تغییر دادند که طرف دوم بسته به مقدار 1+ یا 9+ باشد.
البته تا زمانی که ندانید این رایانهها برای چه مقاصدی استفاده میشدند، ممکن است همه این مسائل گیجکننده به نظر بیایند. در رایانههای ابتدایی برنامه Fortran بر روی یک دستگاه پانج کلید پانچ میشد و همراه با کارتهای داده و کنترل مورد استفاده قرار میگرفت. اما از زمان معرفی رایانه 650 که هیچ دیسکی نداشت، کامپایلر فرترن نیز روی سیستم وجود نداشت. بنابراین برای کامپایل برنامه، کارت کامپایلر فرترن در کارت ریدر قرار میگرفت و سپس متن برنامه فرترن به صورت داده به سیستم وارد میشد. پس از مدت زمانی این دستگاه نتایج محاسبات را روی کارت پانچ میکرد.
سپس دسته کارتهای کتابخانه زمان اجرای فرترن و کارتهای پانچ شده قبلی در کارت ریدر قرار میگرفت و دادههای مورد نیاز برنامه نیز پس از آن وارد سیستم میشد. برنامه اجرا میشد و نتایج آن بر روی دستهای دیگر از کارتها پانچ میشد. برای مشاهده نتایج میبایست کارتهای نتایج را در دستگاه دیگری مانند IBM 407 وارد میکردید تا آنها را بر روی کاغذ چاپ کند (در مواردی که رایانه مانند مدلهای 650 خود پرینتر داخلی نداشت).
رایانههای مین فریم در این زمان نمایشگر نداشتند. رابط کاربری آنها شامل دکمهها، کلیدها و چراغهایی بود. سیستم محاسباتی دو-پنجپنجی نه تنها بررسی خطا انجام میداد؛ بلکه کاربر میتوانست به پنل آن نگاه کرده و بداند که چه دادهای در چه بخشی از ماشین در کدام زمان قرار داشته است:

بنابراین کد 2 از 5 و سیستم محاسباتی دو-پنجپنجی هر دو توانایی بررسی خطا را داشتند؛ اما نگاه کردن به یک عدد در مبنای دو-پنجپنجی و دانستن مقدار دهدهی آن آسانتر بود. این تجربه در نهایت تا حدودی کاربرپسند تر بود.
اگر این نوشته مورد توجه شما قرار گرفته است، احتمالاً به موارد زیر نیز علاقهمند خواهید بود:
- سیستمهای باینری به زبان ساده – بخش اول: اعداد باینری
- آموزش های ویژه علاقهمندان به کامپیوتر
- مجموعه آموزش های مدارهای منطقی (طراحی دیجیتال)
- مجموعه آموزشهای علوم کامپیوتر
- اسکریپت شناسایی توانهای عدد ۲ در پایتون
- آموزش ساختمان داده ها
- مجموعه آموزشهای برنامه نویسی
==












