مفهوم نرخ رشد مرکب سالانه و روش محاسبه آن – به زبان ساده
«نرخ رشد سالانه مرکب» (Compound Annual Growth Rate-CAGR)، میانگین نرخ رشد سالانه یک سرمایهگذاری است که در دورهای طولانیتر از یک سال انجام میپذیرد.


برای محاسبه این شاخص مالی، ابتدا نسبت ارزش سرمایهگذاری در پایان دوره به اول دوره محاسبه میشود. سپس این نسبت به توان معکوس سالهای سرمایهگذاری میرسد و در انتها مقدار ۱ از آن کسر میگردد.
به این ترتیب، شیوه محاسبه آن طبق رابطه زیر خواهد بود:

ممکن است نرخ رشد سالانه مرکب (CAGR) با «نرخ بازگشت واقعی» (True Return Rate) اشتباه گرفته شود. در حقیقت این شاخص عددی، بیانگر نرخ ثابت رشد سرمایه است، که البته هرگز در واقعیت اتفاق نمیافتد. CAGR روشی برای محاسبه ساده و آسان نرخ بازگشت سرمایه است.
یک مثال برای درک بهتر CAGR
فرض کنید سرمایهگذاری به ارزش 10،000 تومان در یک سبد سهام در تاریخ اول فروردین سال ۱۳۹3 انجام شده است. متاسفانه سبد سهام به نرخی ناموزون رشد کرده. فرض کنید ارزش سبد سهام در فروردین سال ۱۳۹۴ مبلغ ۱۳،۰۰۰ تومان، در اول فروردین سال ۱۳۹۵ برابر با ۱۴،۰۰۰ تومان و در اول فروردین ۱۳۹۶ برابر با 19،500 تومان باشد.
مقدار CAGR در طی ۳ سال (دوره 1393 تا 1396) برابر با 24.93٪ خواهد بود. محاسبات مربوطه در زیر دیده میشود:
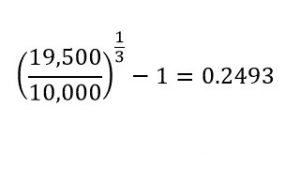
نرخ رشد سالانه مرکب برای این سرمایهگذاری سه ساله که برابر با 24.93٪ است، نسبت کسب سود سالانه از دورهی سرمایهگذاری را نشان میدهد.
کاربردهای CAGR
از آنجایی که CAGR به کمک میانگین نرخ رشد سرمایهگذاری در یک مقطع زمانی محاسبه میشود، شاخصی ساده و قابل درک است. به همین دلیل کاربردهای متنوعی نیز دارد.
با توجه به تغییرات بازار، نرخ رشد سالانه برای یک سرمایهگذاری از سالی به سال دیگر متفاوت است. برای مثال ممکن است یک سرمایهگذاری در سال اول ۸٪ سود و در سال دوم ۲٪ کاهش قیمت داشته باشد و در سال بعد ۵٪ به صاحب سرمایه سود برسد. با توجه به ناهمگونی میزان سود در سالهای مختلف، استفاده از CAGR سرمایهگذار را از وضعیت سبد سهام آگاه میکند.
از این شاخص میتوان برای مقایسه انواع سرمایهگذاریها استفاده کرد. برای مثال در سال 1394 مبلغ 10،000 ریال در یک حساب سپرده با نرخ سود ثبات سالانه 1٪ سرمایهگذاری شده است. در سال 1395 میزان دارایی برابر با 10،100ریال و در سال 1396 برابر با 10،201ریال و در سال 1397 برابر با 10،303.01 ریال خواهد بود.
در همین دوره نیز یک سرمایهگذاری در سال 1394 در بازار بورس روی یک سبد سهام به ارزش 5،000 ریال انجام شده است، که در سال ۱۳۹۵ ارزشی برابر با 5،114 در سال 1396 کاهشی برابر با 5،098 و افزایش ارزشی برابر با 5،437 ریال در سال 1397 است. همانطور که دیده میشود نرخ رشد ثابت نبوده و در سال 1396 ضرر در سرمایهگذاری نیز وجود دارد. محاسبه مربوط به شاخص نرخ رشد سالانه مرکب به صورت زیر خواهد بود.
(5,437/5,000)(1/3)-1 = 0.0283
با توجه به متغیر بودن میزان رشد سرمایهگذاری در این سالها برای مقایسه بین دو شیوه سرمایهگذاری از CAGR استفاده میشود که برای بانک برابر با ۱٪ و برای سبد سهام برابر با 2.83٪ خواهد بود که بسیار بیشتر از نرخ رشد سرمایه در بانک است.
از CAGR برای رصد کردن کارایی کسب و کارهای مختلف در یک یا چند شرکت نیز میتوان استفاده کرد. برای مثال، ممکن است در طی یک دوره ۵ ساله در یک شرکت عمده فروشی، CAGR برای سهم از بازار برابر با 1.82٪ و برای رضایت مشتریان برابر با 0.58-٪ باشد. به این ترتیب استفاده از مقایسه CAGR برای ویژگیهای مختلف یک شرکت، شناسایی نقاط ضعف و قوت را میسر میسازد. همچنین رصد کردن چنین شاخصهایی در بین دیگر شرکتها موقعیت کسب و کار در بازار را نشان میدهد. مثلا CAGR برای میزان رضایت مشتریان در فروشگاههای عمده فروشی در مقایسه با فروش فوق سریع اینترنتی (6.31-٪) در همان دوره زمانی، کم به نظر نمیرسد.
محدودیتهای نرخ رشد مرکب سالانه
استفاده از CAGR مانند شاخصهای دیگر دارای معایبی نیز هست، بنابراین باید همزمان و در کنار سایر مفاهیم به کار گرفته شود.
اولین محدودیت برای CAGR، هموارسازی میانگین روی یک دوره زمانی است بطوری که تغییرات در میان دوره نادیده گرفته شده و رشد در طول دوره ثابت در نظر گرفته شود. بنابراین هنگام استفاده از این شاخص، به مقادیر سالانهای دقت کنید که شاخص در آن دوره محاسبه شده.
محدودیت دیگر در استفاده از CAGR در سرمایهگذاری، گذشته نگر بودن این شاخص است. به این معنی که اگر رشد سرمایهگذاری در یک دوره 5 ساله ثابت باشد، نمیتوان بر اساس شاخص نرخ رشد سالانه مرکب، ارزش سرمایه گذاری را برای سالهای بعد پیشبینی کرد زیرا تغییرات بازار و عواملی دیگری که در نرخ رشد سرمایهگذاری نقش دارند در نظر گرفته نشده است.
سومین محدودیت، تفسیر CAGR است. با فرض اینکه ارزش یک صندوق سرمایهگذاری در سال اول 100،000، در سال دوم 71،000، در سال سوم 44،000، در سال چهارم 81،000 و در سال پنجم 126،000 باشد، نرخ رشد سالانه مرکب برای سه سال آخر برابر با 42.01٪ خواهد بود که به نظر نرخ رشد بالایی است، در حالیکه برای برای دورهی ۵ ساله مقدار CAGR برابر با 4.73٪ محاسبه میشود که قابل مقایسه با دوره سه ساله نیست.
اگر مطلب بالا برای شما مفید بوده است، احتمالاً آموزشهایی که در ادامه آمدهاند نیز برایتان کاربردی باشند.













با سلام و احترام
آیا برای رفع محدودیت نادیده گرفته شدن تغییرات در میان دوره راهکاری ارایه گردیده؟ ممنون میشوم اگر راهنمایی بفرمائید.
سلام وقت بخیر
من یه سوال داشتم با آموزش نتونستم سوالم را حل کنم .
سوالم در مورد سختی شبکه هستش.
سوالم اینه:
نرخ افزایش متوسط ماهانه سختی شبکه را در ۱۲ ماه گذشته محاسبه کرده ،سپس این نرخ را برای ۳ سال آینده در نظر بگیرید؟
نرخ سختی الان:۲۳/۱۳۷۴
نرخ سختی ۱ماه گذشته:۲۱/۴۴۸۳
نرخ سختی ۱سال گذشته:۱۴/۷۱۵۲
سلام و درود،
مشکل مسئله شما در این است که برای محاسبه نرخ رشد مرکب، فاصله زمانی بین اندازهها باید یکسان باشد. در حالیکه نه تنها فاصله یکسان نیست بلکه واحدها نیز یکسان نیستند. ابتدا واحدها (ماه را به سال یا سال را به ماه) تبدیل کنید، سپس میانگین هندسی را بدست آورید.
موفق و تندرست باشید.