تحلیل نحوی (Syntax Analysis) در طراحی کامپایلر – راهنمای جامع
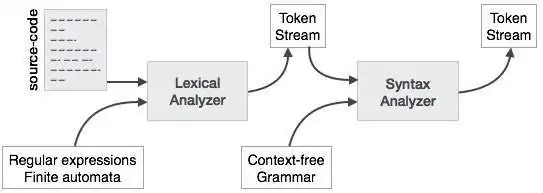
تحلیل نحوی یا تجزیه (Parsing)، فاز دوم کامپایلر است. در این نوشته مفاهیم پایه مورد استفاده در ساخت تجزیهکننده را بررسی میکنیم. در بخشهای قبلی از سلسله مطالب طراحی کامپایلر دیدیم که یک تحلیلگر واژهای میتواند توکنها را با کمک عبارتهای منظم و قواعد الگو شناسایی کند. اما یک تحلیلگر واژهای نمیتواند ساختار یک جمله مفروض را به دلیل محدودیتهای عبارتهای منظم بررسی کند. عبارتهای منظم نمیتوانند از توکنهای متعادلسازی مانند پرانتز استفاده کند. بنابراین، این فاز از «گرامر مستقل از متن» (CFG) استفاده میکند که به عنوان اتوماتای پشتهای (push-down automata) شناخته میشود.


در تصویر فوق مشخص است که گرامر منظم نیز بخشی از گرامر مستقل از متن است؛ اما برخی مشکلات وجود دارند که خارج از حوزه گرامر منظم است. CFG ابزاری مفیدی در توصیف ساختار زبانهای برنامهنویسی محسوب میشود.
گرامر مستقل از متن
در این بخش ابتدا تعریف گرامر مستقل از متن را میبینیم و اصطلاحهای مورد استفاده در فناوری تجزیه (parsing) را بررسی میکنیم.
یک گرامر مستقل از متن چهار مؤلفه دارد:
- مجموعهای از حالتهای غیر پایانی (V). حالتهای غیر پایانی متغیرهای نحوی هستند که مجموعهای از رشتهها نمایش میدهند. حالتهای غیر پایانی مجموعهای از رشتهها را نشان میدهند که به تعریف زبان تولید شده از سوی گرامر کمک میکنند.
- مجموعهای از توکنها که به نام نمادهای پایانی (Σ) نامیده میشوند. نمادهای پایانی نمودارهای پایهای هستند که رشتهها بر مبنای آنها تشکیل مییابند.
- مجموعهای از ترکیبها (P). ترکیبهای گرامر روشی که نمادهای پایانی و غیر پایانی را میتوان برای تشکیل رشتهها ترکیب کرد، تعیین میکنند. هر ترکیب شامل یک نماد غیر پایانی است که سمت چپ ترکیب نامیده میشود و یک پیکان است و یک توالی از توکنها و/یا نمادهای پایانی است که سمت راست ترکیب است.
- یکی از نمادهای غیر پایانی به صورت نماد آغازین (S) تعیین شده است که ترکیب از آن جا آغاز میشود.
رشتهها از نماد آغازین با تعویض مکرر یک نماد غیر پایانی (در ابتدا نماد آغازین) در سمت راست ترکیب مشتق میشوند.
مثال
مسئله کلمات پالیندوم (palindrome) یعنی کلماتی که از هر دو طرف یکسان خوانده میشوند (مانند درد) را در نظر میگیریم. این واژهها را توسط عبارتهای منظم نمیتوان توصیف کرد.. یعنی L = { w | w = wR } یک زبان منظم نیست. اما آن را میتوان به وسیله CFG توصیف کرد که در ادامه مشخص است:
G = (V, Σ, P, S)
که
V = { Q, Z, N }
Σ = { 0, 1 }
P = { Q → Z | Q → N | Q → ℇ | Z → 0Q0 | N → 1Q1 }
S = { Q }
این گرامر، زبان پالیندوم را توصیف میکند: مثلاً 1001, 11100111, 00100, 1010101, 11111, و غیره.
تحلیلگر نحوی
یک تحلیلگر نحوی یا تجزیهکننده، ورودی را از تحلیلگر واژهای به شکل جریانهایی از توکن میگیرد. سپس تجزیهکننده کد منبع (جریان توکن) را بر اساس قواعد ترکیب آنالیز میکند تا خطاهای کد را بیابد. خروجی این فاز درخت تجزیه (Parse tree) است.
بدین ترتیب، تجزیهکننده دو وظیفه دارد، یکی تجزیه کد یعنی گشتن به دنبال خطاها و دیگری تولید درخت تجزیه به صورت خروجی فاز. انتظار میرود که تجزیهکنندهها، کل کد را حتی در صورتی که خطایی در برنامه وجود داشته باشد، تجزیه کنند. تجزیهکنندهها از راهبردهای بازیابی خطا استفاده میکنند که در ادامه در مورد آنها بیشتر صحبت خواهیم کرد.
اشتقاق (Derivation)
اشتقاق اساساً یک توالی از قواعد ترکیب در جهت دریافت رشته ورودی است. در طی تجزیه ما دو تصمیم برای برخی شکلهای جمله ورودی میگیریم:
- تصمیم در مورد نماد غیر پایانی که باید تعویض شود
- تصمیم در مورد قواعد ترکیبی که به وسیله آن نماد غیر پایانی تعویض میشود.
برای تصمیمگیری در مورد این که نماد غیر پایانی باید با قواعد ترکیب جایگزین شود یا نه دو گزینه داریم: اشتقاق چپترین و اشتقاق راستترین.
اشتقاق چپترین
اگر صورت جمله ورودی اسکن شده و از چپ به راست تعویض شود، به نام اشتقاق چپترین نامیده میشود. صورت جملهای اشتقاق یافته به روش اشتقاق چپترین نیز به نام صورت جملهای چپ نامیده میشود.
اشتقاق راستترین
اگر یک ورودی را از سمت راست به چپ اسکن کرده و با قواعد ترکیبی جایگزین کنیم، به نام اشتقاق راستترین نامیده میشود. صورت جملهای اشتقاق یافته از اشتقاق راستترین، به نام صورت جملهای راست شناخته میشود.
نمونه
قواعد ترکیب
E → E + E E → E * E E → id
رشته ورودی: id + id * id
اشتقاق چپترین به صورت زیر است:
E → E * E E → E + E * E E → id + E * E E → id + id * E E → id + id * id
توجه کنید که نماد غیر پایانی سمت چپترین همواره در ابتدا پردازش میشود.
اشتقاق راستترین به صورت زیر است:
E → E + E E → E + E * E E → E + E * id E → E + id * id E → id + id * id
درخت تجزیه
درخت تجزیه (درخت اشتقاق نیز نامیده میشود) یک بازنمایی از اشتقاق محسوب میشود. بدین ترتیب مشاهده شیوه اشتقاق رشتهها از نماد آغازین آسانتر خواهد بود. نماد آغازین به ریشه درخت تجزیه تبدیل میشود. این وضعیت به وسیله مثالی توضیح داده میشود.
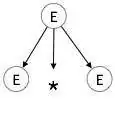
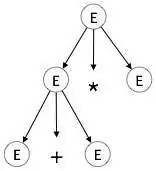
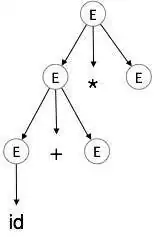
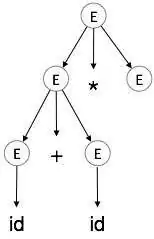
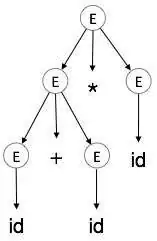
اشتقاق چپترین a + b * c را در نظر بگیرید. اشتقاق چپترین آن به صورت زیر است:
E → E * E E → E + E * E E → id + E * E E → id + id * E E → id + id * id
گام 1:
گام 2:
گام 3:
گام 4:
گام 5:
در یک درخت تجزیه:
- همه گرههای برگ، پایانی هستند.
- همه گرههای داخلی، غیر پایانی هستند.
- پیمایش میانترتیبی، همان رشته ورودی اولیه را به دست میدهد.
یک درخت تجزیه، شرکتپذیری و تقدم عملگرها را نشان میدهد و عمیقترین زیردرخت، در وهله اول پیمایش میشود. از این رو عملگر موجود در آن زیردرخت نسبت به عملگری که در گرههای والدش قرار دارد، تقدم بالاتری دارد.
ابهام
گرامر G در صورتی مبهم خوانده میشود که برای دستکم یک رشته آن، بیش از یک درخت تجزیه (اشتقاق چپ یا راست) وجود داشته باشد.
مثال
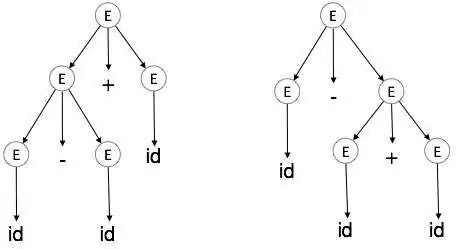
E → E + E E → E – E E → id
گرامر فوق برای رشته id + id – id، دو درخت تجزیه ایجاد میکند:
این زبان توسط یک گرامر مبهم تولید شده است و گفته میشود که دارای ابهام ذاتی (inherently ambiguous) است. ابهام در گرامر برای ساخت کامپایلر خوب نیست. هیچ روشی برای کشف و حذف ابهام به طور خودکار وجود ندارد؛ اما با بازنویسی کل گرامر به صورت بیابهام یا با تعیین و پیروی از قواعد خاص تقدم و شرکتپذیری میتوان آن را از بین برد.
شرکتپذیری
اگر یک عملوند در هر دو سوی خود عملگرهایی داشته باشد، این که این عملوند از عملگر کدام سمت استفاده کند به شرکتپذیری آن عملگرها بستگی دارد. اگر عملیات به صورت شرکتپذیر از چپ باشد در این صوت عملوند از سوی عملگر سمت چپ برداشته میشود و اگر شرکتپذیر از راست باشد، عملگر راست، عملوند را انتخاب میکند.
نمونه
عملیاتهایی مانند جمع، ضرب، تفریق و تقسیم، شرکتپذیر از چپ هستند. اگر عبارتی شامل موارد زیر باشد:
id op id op id
به صورت زیر ارزیابی میشود:
(id op id) op id
(id + id) + id
عملیاتهایی مانند توان شرکتپذیر از راست هستند، یعنی ترتیب ارزیابی در همان عبارت به صورت زیر خواهد بود:
id op (id op id)
id ^ (id ^ id)
تقدم
اگر دو عملگر دارای یک عملوند مشترک باشند، تقدم عملگرها تعیین میکند که کدام یک عملوند را بر میدارند. یعنی 4*3+2 میتواند دو درخت تجزیه داشته باشد، یکی متناظر با 4*(3+2) و دیگری که متناظر با (4*3)+2 است. با تعیین تقدم میان عملگرها، این مسئله را به راحتی میتوان حل کرد. همانند مثال قبلی ازنظر ریاضیاتی * (ضرب) نسبت به +(جمع) تقدم دارد و از این رو عبارت 4*3+2 همواره به صورت زیر تفسیر میشود:
2 + (3 * 4)
این روشها احتمال ابهام را در زبان و گرامر آن کاهش میدهند.
بازگشتی چپ
یک گرامر زمانی بازگشتی چپ نامیده میشود که نماد غیر پایانی A را داشته باشد که اشتقاق آن شامل خود A به عنوان چپترین نماد باشد.
گرامر چپترین یک موقعیت دردسرساز برای تجزیهکنندههای بالا به پایین تلقی میشود. تجزیهکنندههای بالا به پایین از نماد آغازین شروع به تجزیه میکنند که خود یک نماد غیر پایانی است. از این رو وقتی تجزیهکننده با همان نماد غیر پایانی در اشتقاقش مواجه میشود، دیگر نمیتواند در مورد این که کجا باید تجزیه را متوقف کند تصمیم بگیرد و لذا وارد حلقه نامتناهی میشود.
مثال
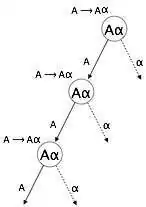
(1) A => Aα | β (2) S => Aα | β A => Sd
- مثال فوق نمونهای از بازگشتی بی درنگ چپ است که در آن A میتواند هر نماد غیر پایانی و آلفا نشان دهنده یک رشته از نمادهای غیر پایانی باشد.
- مثال فوق نمونهای از بازگشتی چپ غیرمستقیم است.
تجزیهکننده بالا به پایین، ابتدا A را تجزیه میکند که به نوبه خود رشتههای شامل خود A ارائه میدهد و تجزیهکننده ممکن است وارد حلقه بی نهایت شود.
حذف بازگشتی چپ
یک روش برای حذف بازگشتی چپ، استفاده از تکنیک زیر است:
ترکیب
A => Aα | β
به ترکیبهای زیر تبدیل میشود
A => βA' A'=> αA' | ε
این کار تأثیری بر رشتههای اشتقاق یافته از گرامر ندارد، اما بازگشتی چپ بی درنگ را حذف میکند. روش دوم استفاده از الگوریتم زیر است که همه بازگشتیهای چپ مستقیم و غیرمستقیم را حذف میکند.
START
Arrange non-terminals in some order like A1, A2, A3,…, A<sub>n</sub>
for each i from 1 to n
{
for each j from 1 to i-1
{
replace each production of form A<sub>i</sub> ⟹Aj?
with A<sub>i</sub> ⟹ δ1? | δ2? | δ3? |…| ?
where A<sub>j</sub> ⟹ δ<sub>1</sub> | δ<sub>2</sub>|…| δ<sub>n</sub> are current A<sub>j</sub> productions
}
}
eliminate immediate left-recursion
END
مثال
مجموعه ترکیب زیر:
S => Aα | β A => Sd
پس از بکار بردن الگوریتم فوق باید به صورت زیر در آید:
S => Aα | β A => Aαd | βd
و سپس بازگشتی چپ بی درنگ را با استفاده از تکنیک نخست حذف میکنیم:
A => βdA' A' => αdA' | ε
اینک هیچ یک از ترکیبها دیگر، بازگشتی چپ مستقیم یا غیرمستقیم ندارند.
فاکتورگیری چپ
اگر بیش از یک قاعده ترکیب گرامری، رشته پیشوندی مشترکی داشته باشد در این صورت تجزیهکننده بالا به پایین نمیتواند تصمیم بگیرد که کدام یک از ترکیبها باید رشته موجود را تجزیه کنند.
مثال
اگر یک تجزیهکننده بالا به پایین با ترکیبی مانند زیر مواجه شود:
A ⟹ αβ | α? | …
در این صورت نمیتواند تصمیم بگیرد که از کدام ترکیب برای تجزیه رشته استفاده کند، زیرا هر دو ترکیبها از نماد پایانی (یا غیر پایانی) یکسانی آغاز میشوند. برای رفع این سردرگمی از تکنیکی استفاده میکنیم که فاکتورگیری چپ نام دارد.
فاکتورگیری چپ گرامر را تبدیل میکند تا آن را برای تجزیهکنندههای بالا به پایین مناسب سازد. در این تکنیک یک ترکیب برای هر یک از پیشوندهای مشترک انتخاب میکنیم و برای اشتقاق با ترکیبهای جدید افزوده میشود.
مثال
ترکیبهای فوق را میتوان به صورت زیر نوشت:
A => αA' A'=> β | ? | …
اینک تجزیهکننده تنها یک ترکیب برای هر پیشوند دارد و راحتتر میتواند تصمیمگیری کند.
مجموعههای اول (First) و پیرو (Follow)
بخش مهمی از ساخت جدول تجزیه در ایجاد مجموعههای اول و پیرو است. این مجموعهها میتوانند موقعیت واقعی هر نماد پایانی را در اشتقاق تعیین کنند. این کار به منظور ایجاد جدول تجزیه انجام مییابد که به وسیله آن میتوان تصمیم گرفت که T[A, t] = α را با برخی از قواعد ترکیبی جایگزین نمود.
مجموعه اول
مجموعه اول برای شناخت نماد پایانی مشتق شده از موقعیت اولیه به وسیله نماد غیر پایانی استفاده میشود. برای مثال:
α → t β
یعنی t (پایانی) در اولین موقعیت از α مشتق میشود. بنابراین (t ∈ FIRST(α.
الگوریتم محاسبه مجموعه اول
به تعریف مجموعه (FIRST(α توجه کنید:
- اگر α پایانی باشد، در این صورت { FIRST(α) = { α .
- اگر α غیر پایانی باشد و α → ℇ یک ترکیب باشد، در این صورت { FIRST(α) = { ℇ .
- اگر αغیر پایانی باشد و α → ?1 ?2 ?3 … ?n و هر یک از اعضای مجموعه (FIRST(? شامل t باشند در این صورت t در (FIRST(α است.
مجموعه اول را میتوان به صورت زیر در نظر گرفت:
مجموعه پیرو (Follow set)
مشابه مجموعه اول در این مورد نیز محاسبه میکنیم که کدام نماد پایانی بی درنگ پس از یک α غیر پایانی در قواعد ترکیب ظاهر میشود. ما آنچه را نمادهای غیر پایانی میتوانند تولید کنند، در نظر نمیگیریم؛ بلکه بررسی میکنیم که نماد پایانی بعدی که از ترکیب یک غیر پایانی پیروی میکند کدام یک میتواند باشد.
الگوریتم محاسبه مجموعه پیرو
- اگر α یک نماد آغازین باشد، در این صورت:
FOLLOW() = $
- اگر α یک غیر پایانی باشد و ترکیب آن به صورت α → AB باشد، در این صورت (First(B به جز ℇ، در (FOLLOW(A قرار دارد.
- اگر α غیر پایانی باشد و ترکیب آن به صورت α → AB باشد که B ℇ است، در این صورت (FOLLOW(A در (FOLLOW(α قرار دارد.
مجموعه پیرو را میتوان به صورت زیر در نظر گرفت:
FOLLOW(α) = { t | S *αt*}
محدودیتهای تحلیلگرهای نحوی
تحلیلگرهای نحوی ورودیهای خود را به شکل توکنهایی از تحلیلگرهای نحوی میگیرند.
تحلیلگرهای نحوی مسئولیت اعتبارسنجی یک توکن ارائه شده از تحلیلگر نحوی را بر عهده دارند. تحلیلگرهای نحوی معایب زیر را دارند:
تحلیلگرهای نحوی:
- نمیتوانند تشخیص دهند آیا یک توکن معتبر است یا نه
- آیا یک توکن پیش از استفاده شدن اعلان شده است یا نه
- آیا یک توکن پیش از استفاده، مقداردهی اولیه شده یا نه
- آیا یک عملیات که بر روی نوعی از توکن اجرا شده معتبر است یا نه.
همه اینها وظایفی هستند که به وسیله تحلیلگر معنایی انجام مییابند که در بخش بعدی این نوشته بررسی خواهیم کرد.
اگر این نوشته مورد توجه شما قرار گرفته است، پیشنهاد میکنیم موارد زیر را نیز بررسی کنید:
- آموزش طراحی کامپایلر
- آموزش تجزیه انتقال (کاهش) در طراحی کامپایلر
- ابزارهای مهندسی کامپیوتر
- مجموعه آموزشهای علوم کامپیوتر
- بررسی مهمترین پروتکلهای زبان برنامهنویسی کلوژر (Clojure)
- آموزش طراحی کامپایلر (مرور و حل تست های کنکور کارشناسی ارشد)
==



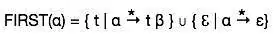











سلام استاد.
اگر توکن غیر مجاز در کد وجود داشته باشه در کدام مرحله خطای سینتکس مربوط به توکن شناسایی ایجاد میشه؟ lexing یا
parsing
بعضی جاها نوشته چون کار لکسر جدا کردن توکن های معنی دار و مجاز زبان هست، تو این مرحله خطا میده
بعضی جاها زدن توکن بی معنی به عنوان ناشناخته در نظر گرفته میشه و به مرحله بعد پارسینگ منتقل میشه و اونجا خطا گرفته میشه