چرخش ها در آرایه های زبان‌ های برنامه نویسی — از صفر تا صد

آرایه‌ ها یکی از متنوع‌ترین ساختمان‌های داده هستند. آرایه‌ها مبنای بسیاری از اپلیکیشن‌ها و الگوریتم‌ها هستند و ساختمان‌های داده زیادی بر مبنای آن‌ها ساخته شده است. برای نمونه الگوریتم جستجوی دودویی بر مبنای آرایه‌ها کار می‌کند، زیرا ساختمان داده آرایه امکان دسترسی تصادفی به محتوای خود را در اختیار ما قرار می‌دهد. اگر دسترسی تصادفی را کنار بگذاریم، دیگر نمی‌توانیم الگوریتم جستجوی دودویی مشهور را با همان پیچیدگی‌های زمانی قبل اجرا کنیم. به طور مشابه ساختمان داده «صف اولویت» (priority queue) را داریم که آن نیز بر مبنای بازنمایی ارائه‌ای از یک درخت دودویی کامل است. خود هیپ نیز یک ریشه بسیاری از اپلیکیشن‌های موجود است. در این مقاله به مسائل برنامه‌نویسی مرتبط با چرخش‌ها در آرایه و رشته‌ها می‌پردازیم. این موضوع، حوزه جالبی از مسائل را شامل می‌شود و در این نوشته قصد داریم دسته‌ای از مسائل را که بر مبنای چرخش‌ها در آرایه هستند بررسی کنیم.

پیش از آغاز بررسی مسائل واقعی ابتدا باید برخی نمونه‌های چرخش را بررسی کرده و تلاش کنیم به سؤالات زیر در مورد چرخش‌ها پاسخ دهیم:

1. چرخش چیست؟
2. چه تعداد چرخش برای آرایه‌ای با N عنصر امکان‌پذیر است؟
3. پیچیدگی زمانی چرخش یک آرایه به میزان یک عنصر چقدر است؟
4. روش‌های میانبر پایتون برای پیاده‌سازی چرخش کدام هستند؟

در ادامه تلاش می‌کنیم به پرسش‌های فوق پاسخ دهیم.

چرخش چیست؟

نمودار زیر ماهیت واقعی چرخش را به طور نسبتاً روشنی مشخص می‌سازد.

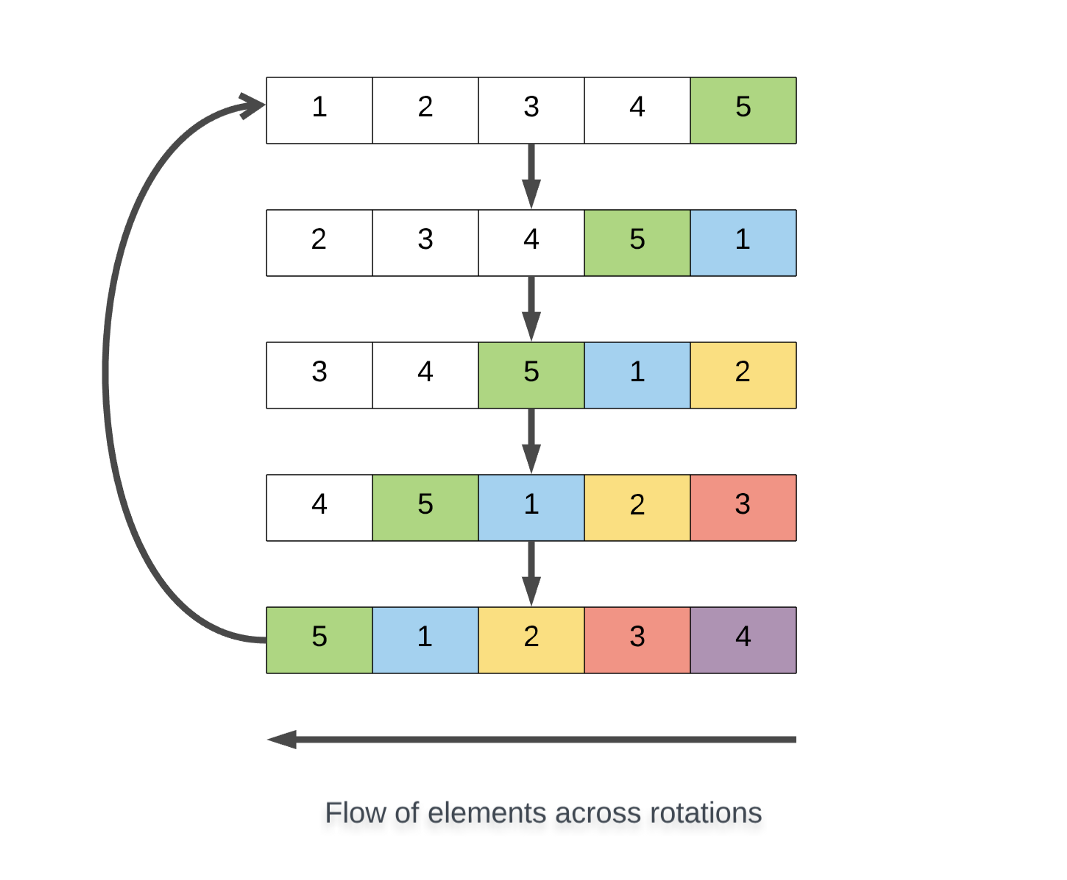
در روش فوق ما نخستین عنصر آرایه را برمی‌داریم و آن را در انتهای آرایه قرار می‌دهیم، سپس عناصر باقیمانده را یک گام به سمت چپ انتقال می‌دهیم. این نمونه‌ای از چرخش چپ است.

فیلم آموزش آرایه ها در زبان برنامه نویسی C (رایگان) در فرادرس

کلیک کنید

به طور مشابه می‌توانیم چرخش راست نیز داشته باشیم.

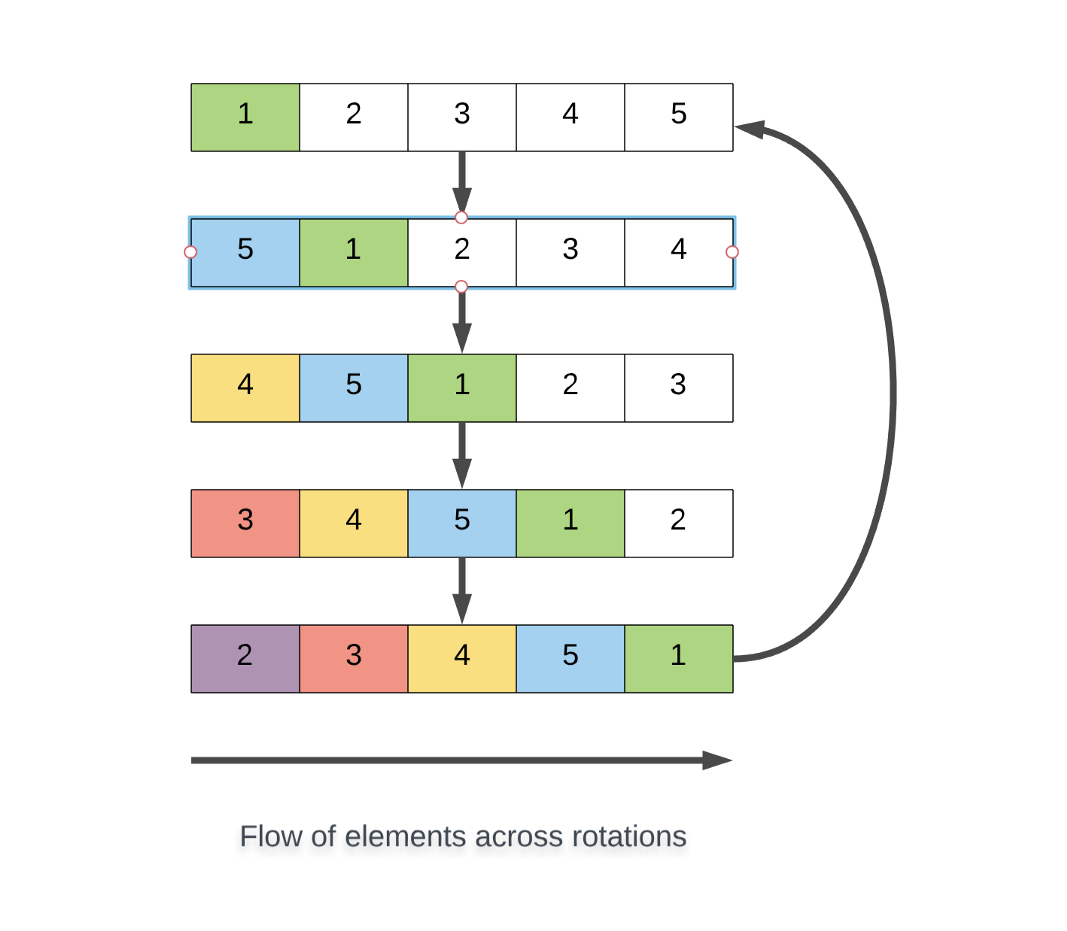
تعداد چرخش‌ها چقدر است؟

نمودارهای فوق کاملاً روشن هستند. ما در صورتی که چرخش چپ با چرخش راست داشته باشیم، برای یک آرایه N عنصری همواره N آرایه چرخش یافته (با احتساب خودش) می‌توان داشت.

پیچیدگی زمانی چرخش چقدر است؟

کاری که ما در چرخش انجام می‌دهیم، این است که عنصر نخست (با فرض چرخش چپ) را برمی‌داریم و سپس همه عناصر باقیمانده را یک گام به سمت چپ انتقال می‌دهیم و در نهایت عنصر برداشته شده را در انتهای آرایه درج می‌کنیم.

فیلم آموزش الگوریتم ها و روش های جست و جو در آرایه (رایگان) در فرادرس

کلیک کنید

از آنجا که هر بار ما یک چرخش (به سمت راست یا چپ) انجام می‌دهیم، n-1 عنصر باقی مانده باید انتقال یابند تا چرخش اجرا شود، پیچیدگی زمانی این عملیات برابر با (O(N است.

روش پایتون برای اجرای چرخش

روش‌های زیادی برای انجام چرخش در پایتون وجود دارند. ما در ادامه تنها روش‌هایی که برای چرخش چپ مورد نیاز هستند را معرفی می‌کنیم چون چرخش راست نیز به طور مشابهی اجرا می‌شوند.

def left_rotate(arr):
    if not arr:
        return arr
    
    left_most_element = arr[0]
    length = len(arr)
    
    for i in range(length - 1):
        arr[i], arr[i + 1] = arr[i + 1], arr[i]
    
    arr[length - 1] = left_most_element
return arr

این ابتدایی‌ترین روش برای پیاده‌سازی یک مرحله از چرخش چپ برای آرایه مفروض است. ما به سادگی عنصر نخست را در انتهای آرایه قرار می‌دهیم و قبل از آن همه عناصر باقیمانده یعنی با آغاز از 1 (برای آرایه با اندیس آغازین 0) یک گام به سمت چپ می‌بریم.

این رویکرد در واقع به اصلاح آرایه اصلی پایان می‌یابد. در موارد زیادی ما تنها نسخه چرخش یافته آرایه را لازم داریم و یا به همه مراحل چرخش آرایه مفروض نیاز داریم؛ اما ما نمی‌خواهیم آرایه اصلی را تغییر دهیم. می‌توان فرض کرد که آرایه اصلی یک ساختمان داده صرفاً-خواندنی است.

اگر به دقت توجه کنید برای اجرای چرخش چپ برای N اُمین بار، باید نتیجه چرخش قبلی را در دست داشت. بنابراین برای نمونه اگر آرایه اصلی ارائه شده به ما به صورت [1,2,3,4,5] باشد و بخواهیم متد فوق را اجرا کنیم، پس از یک چرخش این آرایه به صورت [2,3,4,5,1] درمی‌آید و سپس می‌توانیم چرخش چپ را مجدداً روی آن اعمال کنیم و نتیجه [3,4,5,1,2] خواهد بود.

با دنبال کردن متد فوق به دست آوردن آرایه‌ای که پس از N چرخش باقی می‌ماند واقعاً دشوار خواهد بود. در ادامه روشی جالب برای رسیدن به این نتیجه ارائه شده است.

def left_rotate(arr, N):
    if not arr:
        return arr
    
    L = len(arr)
    rotated_array = []
    for i in range(N, N + L):
        rotated_array.append(arr[i % L])
return rotated_array

ترفندی که در اینجا استفاده شده، این است که از عملیات «پیمانه» (modulo) بهره گرفته‌ایم. اگر به آرایه‌های چرخش یافته توجه کنید می‌بینید که گویا نقطه آغازین برای آرایه چرخش یافته در واقع یک اندیس مانند i در آرایه اصلی است. این اندیس i می‌تواند بر اساس عدد N مشخص شود که نشان‌دهنده تعداد چرخش‌هایی است که می‌خواهیم روی آرایه مفروض اجرا کنیم و سپس نتیجه را بازگشت دهیم.

ضمناً همان‌طور که می‌توانید تصور کنید، N می‌تواند به میزان زیادی نیز بزرگ باشد. در واقع N می‌تواند بزرگ‌تر از طول آرایه اصلی باشد. با این وجود، پس از طی زمان مشخصی، آرایه چرخش یافته شروع به تکرار خود می‌کند. برای آرایه‌ای با اندازه N پس از N-1 چرخش، آرایه چرخش یافته بعدی که به دست می‌آید همان آرایه اصلی است.

برای درک دلیل این که عملیات modulo چگونه کار می‌کند، باید نگاهی به نمودار زیر بیندازیم که چندین چرخش را نشان می‌دهد.

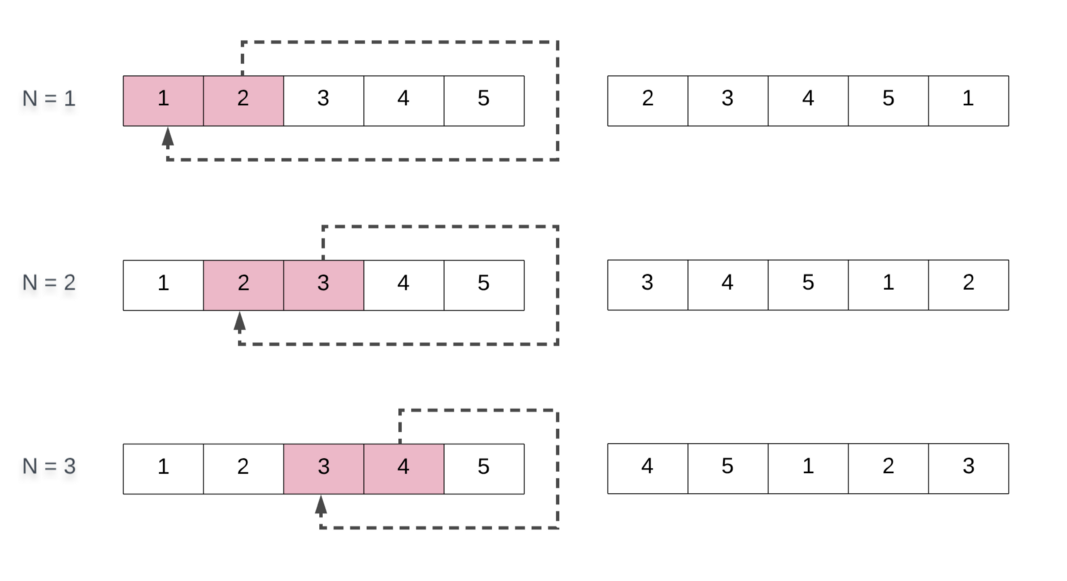
امیدواریم این نمودار شفافیت مورد نیاز برای درک علت استفاده از عملیات پیمانه و دلیل این که می‌توانیم مستقیماً پس از اجرای N چرخش روی آن آرایه را دریافت کنیم در اختیار شما قرار دهد.

به جای نوشتن کدی مانند قطعه کد فوق، می‌توانیم کدی مانند زیر در پایتون بنویسیم:

def left_rotate(arr, N):
    if not arr:
        return arr
return [arr[i % len(arr)] for i in range(N, N + len(arr))]

اکنون که درکی از چرخش‌ها پیدا کردیم و می‌دانیم که چگونه با آرایه‌های خود کار کنیم، می‌توانیم برخی مسائل جالب را با موضوع مفهوم چرخش در آرایه بررسی کنیم.

چرخش رشته‌ها

فرض کنید دو رشته به نام‌های A و B داریم که طول آن‌ها ممکن است یکسان باشد یا نباشد. اینک می‌خواهیم در صورتی که هر چرخش خاصی از رشته A بتواند رشته B را تولید بکند، مقدار true بازگشت دهیم.

فیلم آموزش آرایه در ساختمان داده ها (مرور – تست کنکور ارشد) (رایگان) در فرادرس

کلیک کنید

در نمودار زیر ما دو رشته A = abcde و B = cdeab را ملاحظه کنید و پس از دو چرخش، رشته A برابر با رشته B خواهد بود. در این حالت می‌توانیم مقدار True بازگردانیم.

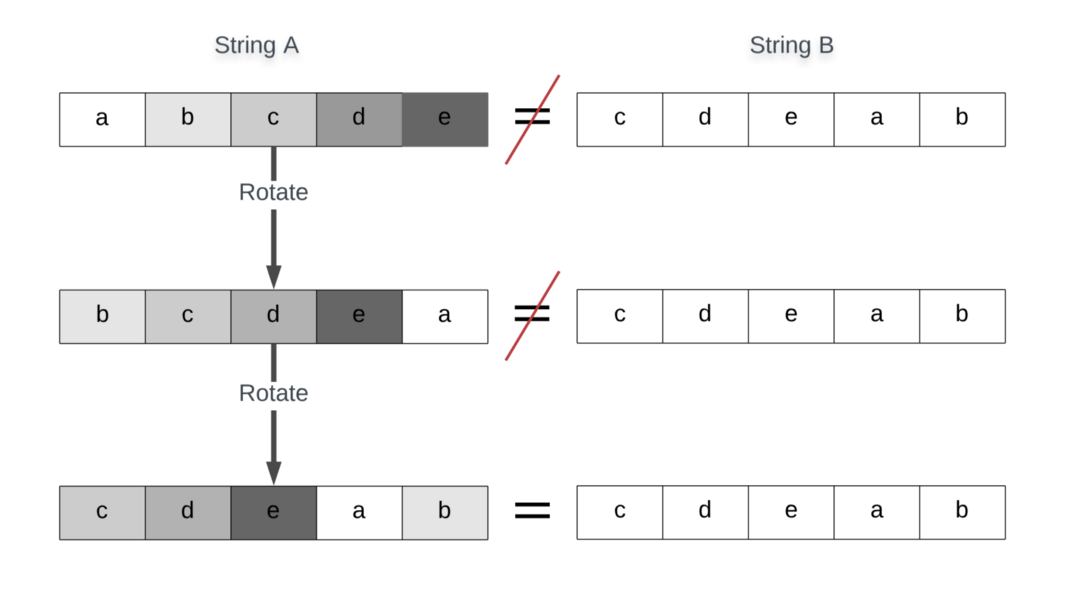
یک بررسی ساده که قطعاً مقدار False بازمی‌گرداند، مواردی است که دو رشته طول متفاوتی دارند. در این حالت مهم نیست که چند چرخش اجرا شود، چون رشته‌ها هرگز نمی‌توانند برابر باشند.

یک روش بسیار ابتدایی برای حل این مسئله یافتن همه چرخش‌ها و سپس مطابقت رشته‌های حاصل با رشته B است تا ببینیم آیا دو رشته برابر خواهند بود یا نه. ابتدا این راه‌حل را بررسی می‌کنیم و سپس تحلیل پیچیدگی آن را می‌بینیم و در نهایت به میزان مناسب بودن آن در مقایسه با راه‌حل‌های دیگر می‌پردازیم.

class Solution:
    def get_rotation(self, arr, N):
        return [arr[i % len(arr)] for i in range(N, N + len(arr))]
    
    def rotateString(self, A, B):
        """
        :type A: str
        :type B: str
        :rtype: bool
        """
        if len(A) != len(B):
            return False
        
        # Convert to lists as strings are immutable and it is always easier to play with 
        # lists than strings especially if modifications are involved.
        A = list(A)
        B = list(B)
        
        L = len(A)
        result = A == B
        for i in range(1, L):
            # If any rotation of A matches B, then return True.
            if self.get_rotation(A, i) == B:
                return True
        return result    

• پیچیدگی زمانی این راه‌حل $$O(N^2)$$ است چون هر چرخش که انجام می‌یابد باید یک مطابقت رشته نیز بین دو رشته به طول N صورت دهیم که به طور کلی (O(N چرخش خواهیم داشت.
• پیچیدگی فضایی این راه‌حل برابر با (O(N است، زیرا یک فهرست جدید در هر چرخش ایجاد می‌شود.

در نمودار زیر می‌بینید که این راه‌حل، عملکرد ضعیفی در قیاس با راه‌حل‌های دیگر دارد.

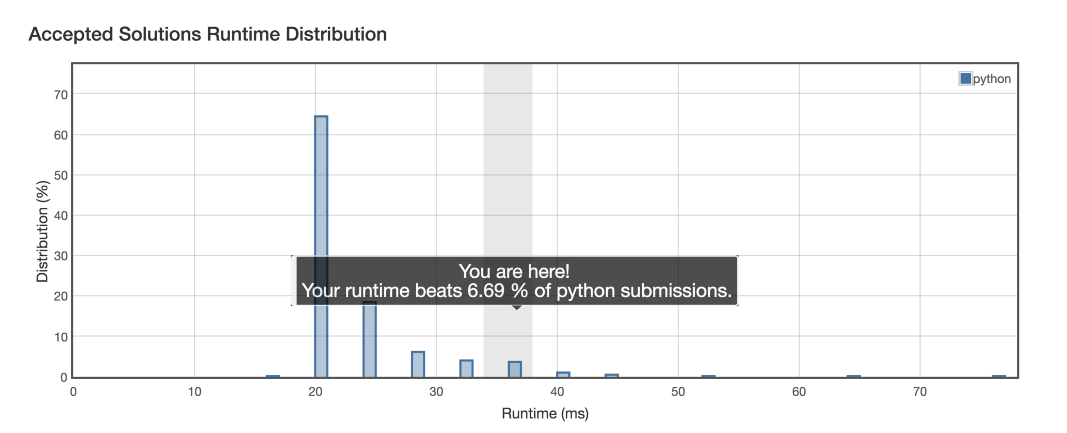
بنابراین ما می‌توانیم بهتر از این نیز عمل کنیم. ایده اصلی چنین است که رشته A را به خودش الحاق کنیم و سپس بررسی کنیم که آیا رشته B زیررشته‌ای از رشته A+A است یا نه.

شاید بپرسید چرا باید چنین کاری بکنیم. پاسخ این است که مشخص شده اگر یک آرایه/رشته را به خودش الحاق کنیم، آرایه یا رشته حاصل همه چرخش‌های آرایه اصلی را پوشش می‌دهد. در ادامه نگاهی به نمودار زیر می‌اندازیم تا ببینیم این عملیات الحاق چگونه همه چرخش‌های ممکن را ارائه می‌کند. رشته‌ای که بررسی می‌کنیم برای این نمودار به صورت abcd است و بنابراین پس از الحاق این رشته با خودش به صورت abcdeabcde درمی‌آید.

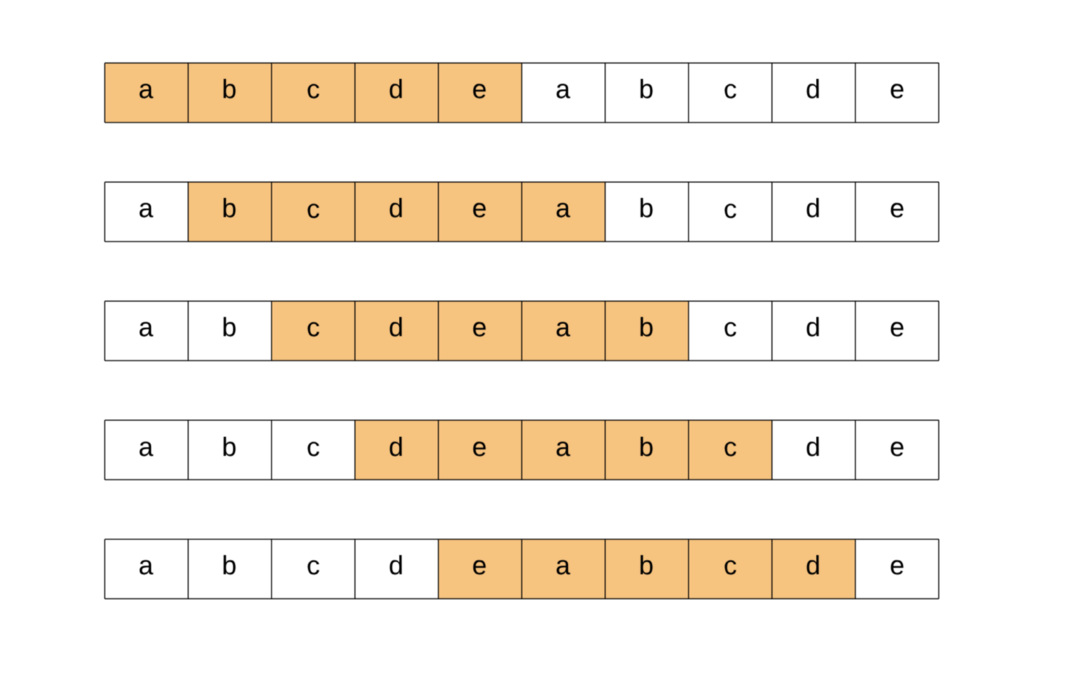
اکنون اگر رشته A یا هر چرخش دیگر A در عمل برابر با رشته B باشد، در این صورت رشته B می‌تواند زیررشته‌ای از این رشته بسط یافته 2A باشد.

• پیچیدگی زمانی این راه‌حل برابر با (O(N است، زیرا همه کاری که انجام می‌دهیم مطابقت رشته بین یک رشته با اندازه N و رشته دیگر با اندازه 2N است.
• پیچیدگی فضایی این راه‌حل برابر با (O(N است، زیرا باید یک رشته جدید به طول 2N ایجاد کنیم تا نسخه بسط یافته رشته A را در آن جای دهیم.

این الگوریتم بسیار سریع‌تر از الگوریتم قبلی است و پیاده‌سازی آن نیز بسیار کوتاه‌تر است.

class Solution:
    def get_rotation(self, arr, N):
        return [arr[i % len(arr)] for i in range(N, N + len(arr))]
    
    def rotateString(self, A, B):
        """
        :type A: str
        :type B: str
        :rtype: bool
        """
        if len(A) != len(B):
            return False
        
        # Convert to lists as strings are immutable and it is always easier to play with 
        # lists than strings especially if modifications are involved.
        A = list(A)
        B = list(B)
        
        L = len(A)
        result = A == B
        for i in range(1, L):
            # If any rotation of A matches B, then return True.
            if self.get_rotation(A, i) == B:
                return True
        return result    

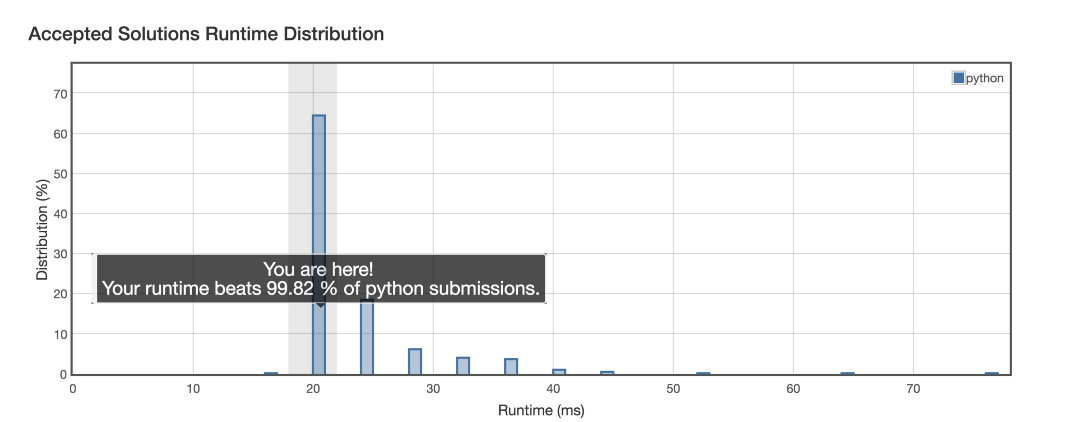
اینک مسئله جالب دیگری را بررسی می‌کنیم که به ظاهر ساده به نظر می‌رسد، اما چند دام دارد که باید پیش از رسیدن به راه‌حل کامل از آن‌ها عبور کنیم.

در این مسئله باید کوچک‌ترین عنصر را در آرایه‌ای مرتب‌شده، چرخش یافته و بدون هیچ عنصر تکراری بیابیم. یک روش بسیار ابتدایی برای حل کردن این سؤال آن است که به دنبال کل آرایه بگردیم و کمترین عنصر ممکن را پیدا کنیم. اما این رویکرد مرتب بودن این آرایه را نادیده می‌گیرد و از این رو یک روش چندان مناسب برای حل این مسئله محسوب نمی‌شود. بنابراین ابتدا باید یک راه‌حل مبتنی بر جستجوی خطی برای این سؤال پیدا کنیم.

class Solution:
    def get_rotation(self, arr, N):
        return [arr[i % len(arr)] for i in range(N, N + len(arr))]
    
    def rotateString(self, A, B):
        """
        :type A: str
        :type B: str
        :rtype: bool
        """
        if len(A) != len(B):
            return False
        
        # Convert to lists as strings are immutable and it is always easier to play with 
        # lists than strings especially if modifications are involved.
        A = list(A)
        B = list(B)
        
        L = len(A)
        result = A == B
        for i in range(1, L):
            # If any rotation of A matches B, then return True.
            if self.get_rotation(A, i) == B:
                return True
        return result    

• در صورتی که N عنصر در آرایه مفروض وجود داشته باشند، پیچیدگی زمانی راه‌حل فوق برابر با (O(N است.
• پیچیدگی فضایی این راه‌حل برابر با (O(1 است.

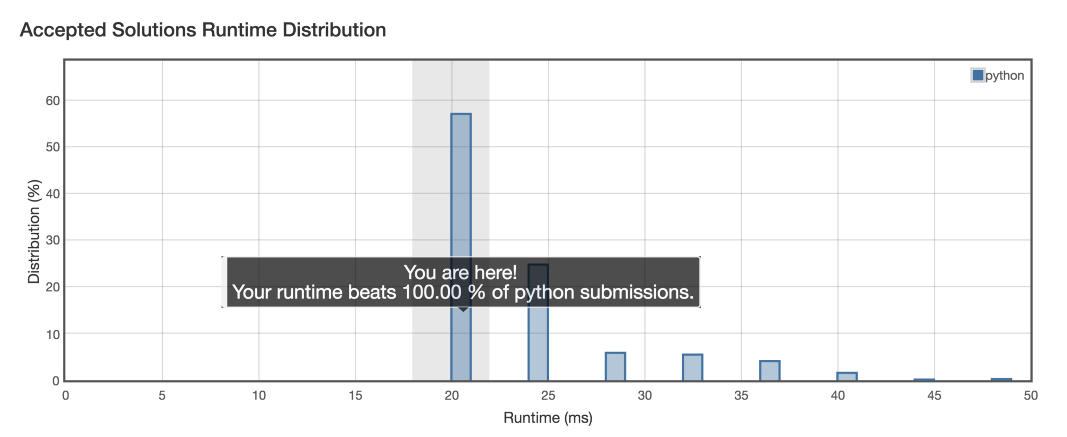
می‌بینیم که این راه‌حل دقیقاً بهترین راه‌حل ممکن است و این واقعیت جالبی است. یک الگوریتم (O(N بهترین زمان اجرایی را به دست می‌دهد. با این وجود، مشخص می‌شود که می‌توانیم این کار را به روشی بسیار بهتر انجام دهیم، زیرا پیچیدگی مجانبی نیز برای ما مهم است.

این واقعیت که آرایه مزبور مرتب‌شده است، سرنخ مهمی محسوب می‌شود. از آنجا که آرایه مرتب‌شده است و می‌خواهیم عنصری را در این آرایه پیدا کنیم، می‌توانیم از پارادایم جستجوی دودویی استفاده کنیم.

با این وجود، آرایه چرخش یافته است. از این رو این که فکر کنیم می‌توانیم به سادگی از جستجوی دودویی استفاده کنیم اشتباه است.

در این سؤال ما اساساً از نسخه اصلاح‌شده‌ای از جستجوی دودویی استفاده می‌کنیم که در آن شرطی (condition) که جهت جستجو را تعیین می‌کند، کاملاً متفاوت از جستجوی دودویی استاندارد است. در یک الگوریتم جستجوی دودویی استاندارد به صورت زیر عمل می‌کنیم:

1. while left <= right
2. mid = (left + right) / 2
3. if element == middle element:
4. return mid
5. elif element < middle element:
6. move to the left i.e. [left, mid - 1]
7. else:
8. move to the right i.e. [mid + 1, right].

از آنجا که آرایه مورد بررسی، مرتب‌شده است، قطعاً می‌توانیم الگوریتم جستجوی دودویی را در مورد آن استفاده کنیم تا یک عنصر را جستجو کند. تنها نکته این است که عناصر چرخش یافته‌اند و این که باید به نحوی این چرخش را به حساب بیاوریم.

اینک سؤال این است که چگونه می‌توانیم بفهمیم که آیا یک آرایه چرخش یافته است یا نه؟ اگر آرایه چرخش نیافته باشد و آرایه با ترتیب صعودی مرتب‌شده باشد، در این صورت:

last_element > first_element

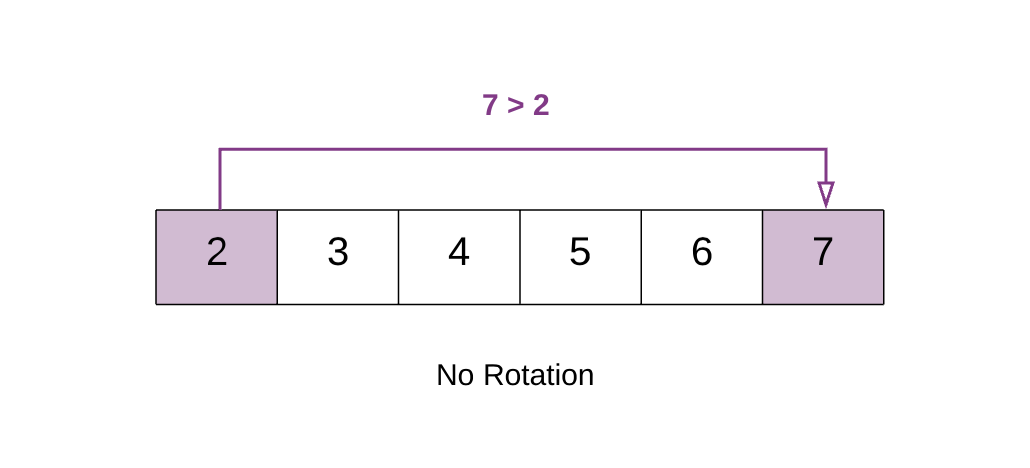
در مثال فوق 7>2 است. این بدان معنی است که آرایه هیچ چرخشی ندارد. در این حالت، می‌توانیم به سادگی عنصر نخست آرایه را که می‌تواند کمترین عنصر باشد بازگشت دهیم.

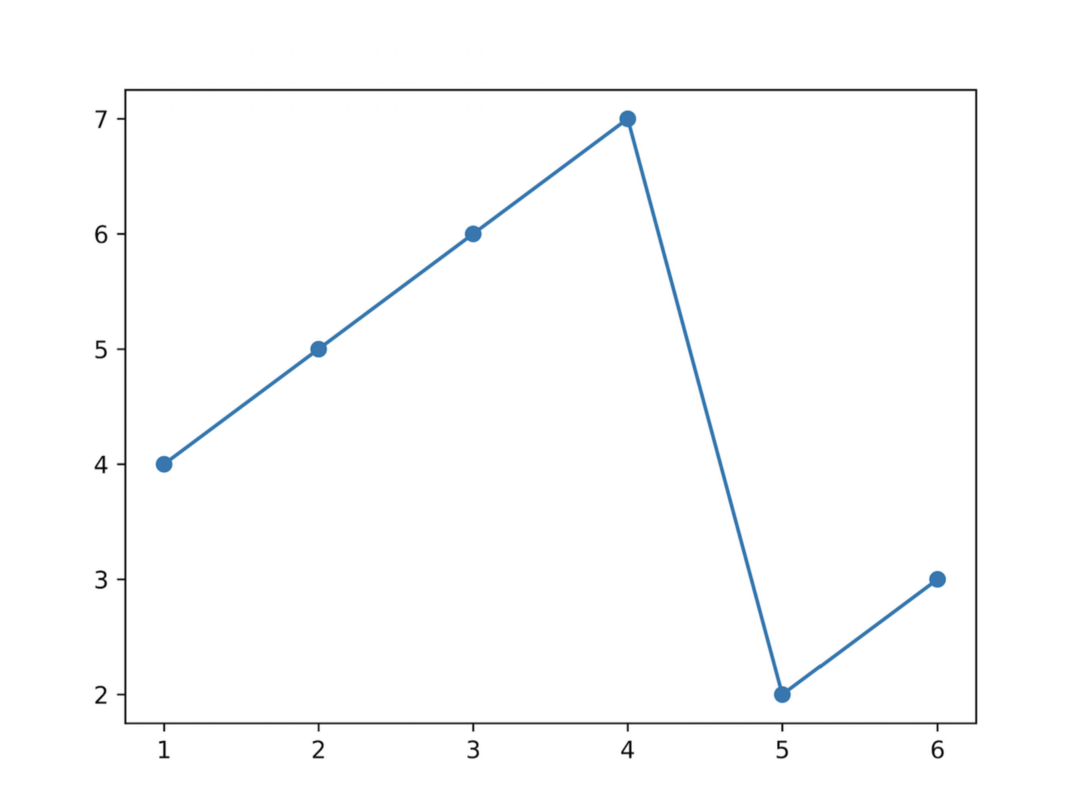
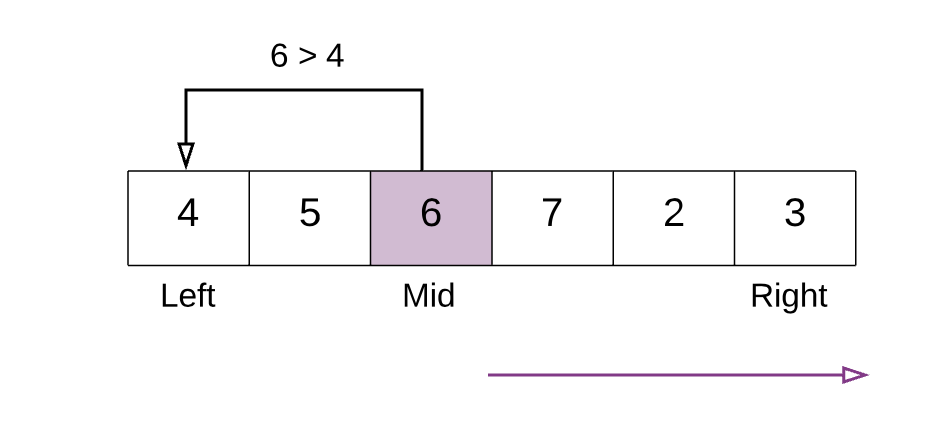
با این وجود، اگر آرایه در عمل چرخش یافته باشد، در این صورت یک حالت پرش، جایی در آرایه رخ داده است. اگر به تصویر زیر نگاه کنید معنی وقوع پرش را متوجه می‌شوید:

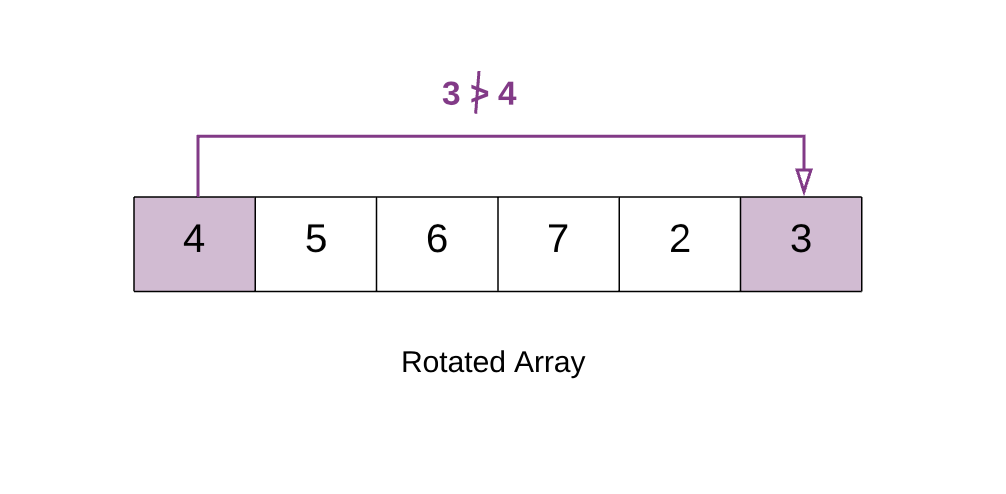
اگر به عناصر آرایه فوق نگاه کنید، چنان که انتظار داریم، دارای ترتیب صعودی هستند، چون آرایه با ترتیب صعودی است. با این وجود، پس از عنصر 7 یک افت ناگهانی در مقادیر وجود دارد و سپس مقدارها مجدداً شروع به افزایش می‌کنند. این همان ساختار پرش یافته است که در مورد آن صحبت می‌کردیم.

در آرایه فوق 3<4 است. از این رو آرایه چرخش یافته است. این امر به این دلیل رخ داده است که آرایه در ابتدا به صورت [2, 3,4,5,6,7] بوده است. اما پس از چرخش، عناصر کوچک‌تر [2,3] به عقب رفته‌اند، یعنی به صورت [4, 5, 6, 7, 2, 3] درآمده است. به همین دلیل، نخستین عنصر [4] در آرایه چرخش یافته بزرگ‌تر از آخرین عنصر می‌شود.

ساختار پرشی که در نمودار فوق مشخص است، بدین معنی است که این همان نقطه‌ای است که تغییری رخ داده است و این همان نقطه‌ای است که می‌تواند به حل سؤال ما کمک کند. ما این نقطه را Inflection Point می‌نامیم.

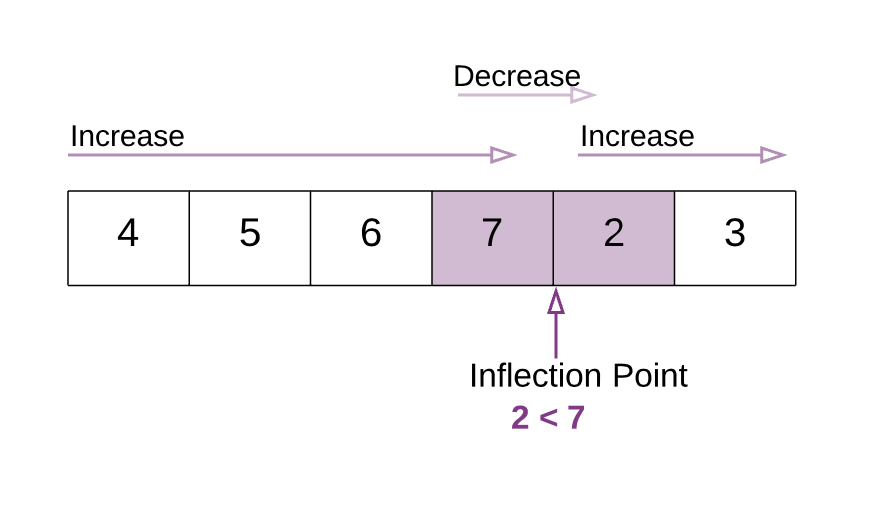
یک خصوصیت مهم نقطه inflection که می‌تواند در حل این مسئله کمک کند به صورت زیر است:

• همه عناصر در سمت چپ نقطه inflection، بزرگ‌تر از عنصر نخست آرایه هستند.
• همه عناصر سمت راست نقطه inflection، کوچک‌تر از عنصر نخست آرایه هستند.

فیلم آموزش آرایه ها در زبان برنامه نویسی C (رایگان) در فرادرس

کلیک کنید

اینک نگاهی به الگوریتم مورد نیاز برای حل این سؤال پیش از پیاده‌سازی آن خواهیم داشت.

1. عنصر میانه (mid) آرایه را پیدا کن.
2. اگر عنصر میانه بزرگ‌تر از عنصر نخست آرایه باشد، این بدان معنی است که باید به دنبال نقطه inflection در سمت راست میانه باشیم.
3. اگر عنصر میانه کوچک‌تر از عنصر نخست آرایه باشد، یعنی باید به دنبال نقطه inflection در سمت چپ میانه باشیم.

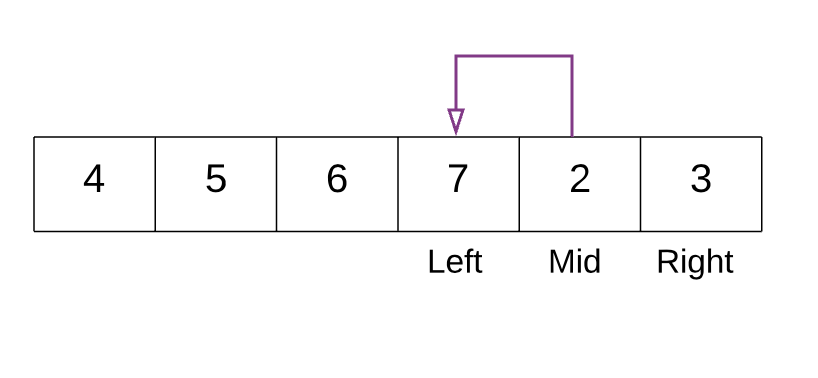
زمانی که نقطه inflection را بیابیم، جستجوی خود را متوقف می‌کنیم. یعنی باید یکی از شرایط زیر برقرار باشد:

• [nums[mid] > nums[mid + 1 از این رو mid+1 کوچک‌ترین عنصر است.
• [nums[mid - 1] > nums[mid از این رو mid کوچک‌ترین عنصر است.

class Solution(object):
    def findMin(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        # If the list has just one element then return that element.
        if len(nums) == 1:
            return nums[0]

        # left pointer
        left = 0
        
        # right pointer
        right = len(nums) - 1

        # if the last element is greater than the first element then there is no rotation.
        # e.g. 1 < 2 < 3 < 4 < 5 < 7. Already sorted array.
        # Hence the smallest element is first element. A[0]
        if nums[right] > nums[0]:
            return nums[0]

        # Binary search way
        while right >= left:
            
            # Find the mid element
            mid = (left + right) / 2
            
            # if the mid element is greater than its next element then mid+1 element is the smallest
            # This point would be the point of change. From higher to lower value.
            if nums[mid] > nums[mid + 1]:
                return nums[mid + 1]
            
            # if the mid element is lesser than its previous element then mid element is the smallest
            if nums[mid - 1] > nums[mid]:
                return nums[mid]

            # if the mid elements value is greater than the 0th element this means
            # the least value is still somewhere to the right as we are still dealing with elements greater than nums[0]
            if nums[mid] > nums[0]:
                left = mid + 1
            else:
                # if nums[0] is greater than the mid value then this means the smallest value is somewhere to the left
right = mid - 1

• پیچیدگی زمانی این راه‌حل برابر با (O(LogN است، چون تنها کاری که باید انجام دهیم استفاده از الگوریتم جستجوی دودویی است و از این رو از ماهیت مرتب‌شده آرایه اصلی استفاده می‌کنیم.
• پیچیدگی فضایی این راه‌حل برابر با (O(1 است.

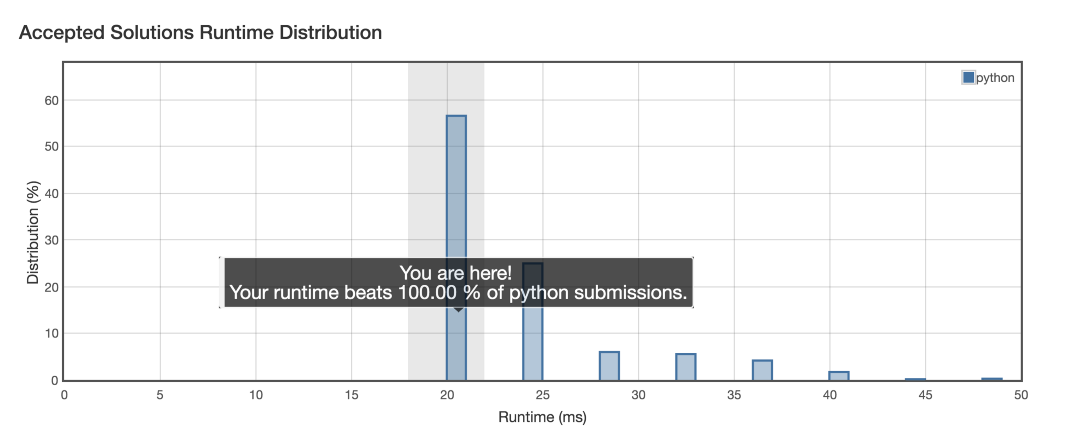
می‌بینیم که این بهترین راه‌حلی است که می‌توان اجرا کرد.

فیلم آموزش الگوریتم ها و روش های جست و جو در آرایه (رایگان) در فرادرس

کلیک کنید

نکته مهم این سؤال آن است که هیچ عنصر تکراری در آرایه وجود ندارد. اما اگر عنصر تکراری نیز در آرایه وجود داشته باشد، چطور؟ آیا ما می‌توانیم همچنان از رویکرد مشابهی برای حل این مسئله استفاده کنیم؟

پاسخ به این سؤال هم بله و هم خیر است. همان مفاهیمی که در بخش قبل بررسی کردیم را می‌توان روی نسخه اصلاح‌شده مسئله نیز استفاده کرد؛ اما دیگر تضمینی وجود ندارد که پیچیدگی زمانی برابر با (O(LogN باشد. به مثال‌های زیر نگاه کنید:

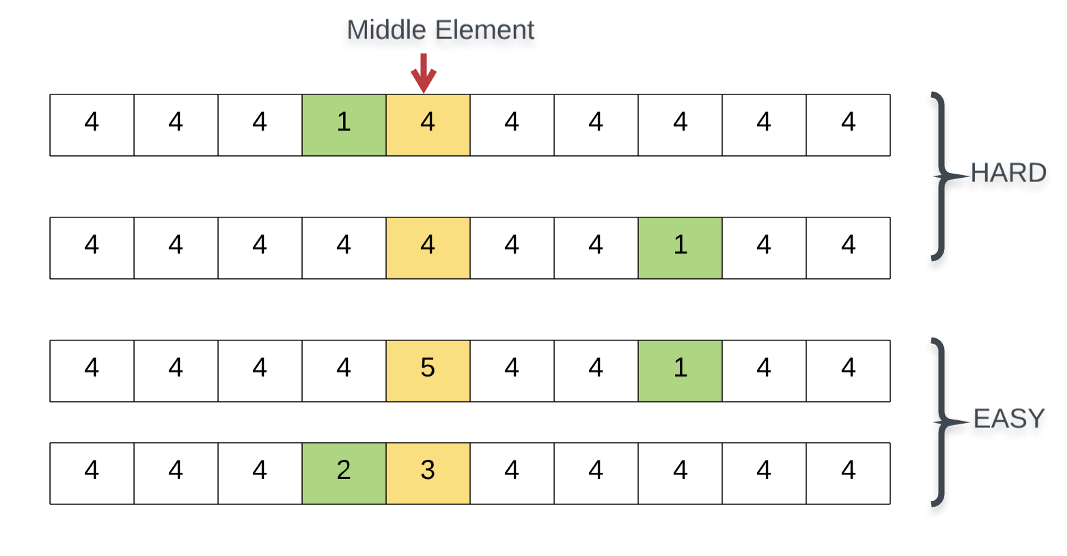
دو مورد که در شکل فوق در بخش پایینی هستند راحت‌تر می‌توانند حل شوند، زیرا عنصر میانی از عنصر اول و آخر متفاوت است و می‌تواند به جهت‌دهی جستجوی دودویی کمک کند. هر چند در ادامه با قرار گرفتن 4 به عنوان عنصر میانه دوباره گیر می‌افتیم.

نکته این است که چون عناصر میانی در این حالت مجاز هستند، امکان داشتن سناریویی مانند زیر وجود خواهد داشت:

عنصر سمت چپ == عنصر میانی === عنصر سمت راست

زمانی که این سناریو وجود داشته باشد، چگونه می‌توان تصمیم گرفت که باید در چه جهتی جستجو کرد؟ هیچ راهی برای دانست این که کدام جهت می‌تواند از سوی الگوریتم جستجوی دودویی نادیده گرفته شود، وجود ندارد. از این رو باید هر دو حالت را بررسی کنیم و آن‌ها را پردازش کنیم و در صورتی که همه عناصر در آرایه یکسان باشند یعنی به صورت [4,4,4,4,4,4,4,4] باشد، در این صورت می‌توانیم در نهایت پردازش هر یک از عناصر را به صورت یک به یک پردازش کنیم.

بنابراین می‌توانیم نتیجه بگیریم که هیچ راهی برای تضمین این که پیچیدگی زمانی این الگوریتم می‌تواند برابر با (O(LogN باشد در دست نداریم. بدترین حالت برای پیچیدگی زمانی در نسخه اصلاح‌شده از الگوریتم جستجوی دودویی که در بالا دیدیم برابر با (O(N است. اینک به سؤال آخر این مقاله می‌پردازیم.

صف مرتب

فرض کنید یک رشته مرتب S با حروف کوچک وجود دارد. در این صورت می‌توانیم هر تعداد حرکت اجرا کنیم. در هر حرکت تعداد دلخواه K حرف با آغاز از چپ انتخاب و از ابتدا حذف کرده و به انتهای رشته انتقال می‌دهیم. اینک می‌خواهیم از نظر الفبایی کوچک‌ترین رشته ممکن را پس از هر تعداد حرکت بازگشت دهیم.

فیلم آموزش آرایه در ساختمان داده ها (مرور – تست کنکور ارشد) (رایگان) در فرادرس

کلیک کنید

ابتدا و قبل از بررسی راه‌حل‌ها، برخی چرخش‌های ممکن برای رشته را بررسی می‌کنیم. رشته‌ای که در نظر داریم baaca است و k را برابر با 3 در نظر می‌گیریم. این بدان معنی است که می‌توانیم هر یک از سه کاراکتر نخست را انتخاب کرده و آن را از جای خود برداشته و به انتهای رشته ببریم و در نهایت همه کاراکترها را به یک گام به سمت چپ ببریم تا این عنصر جدید در انتخاب رشته قرار گیرد.

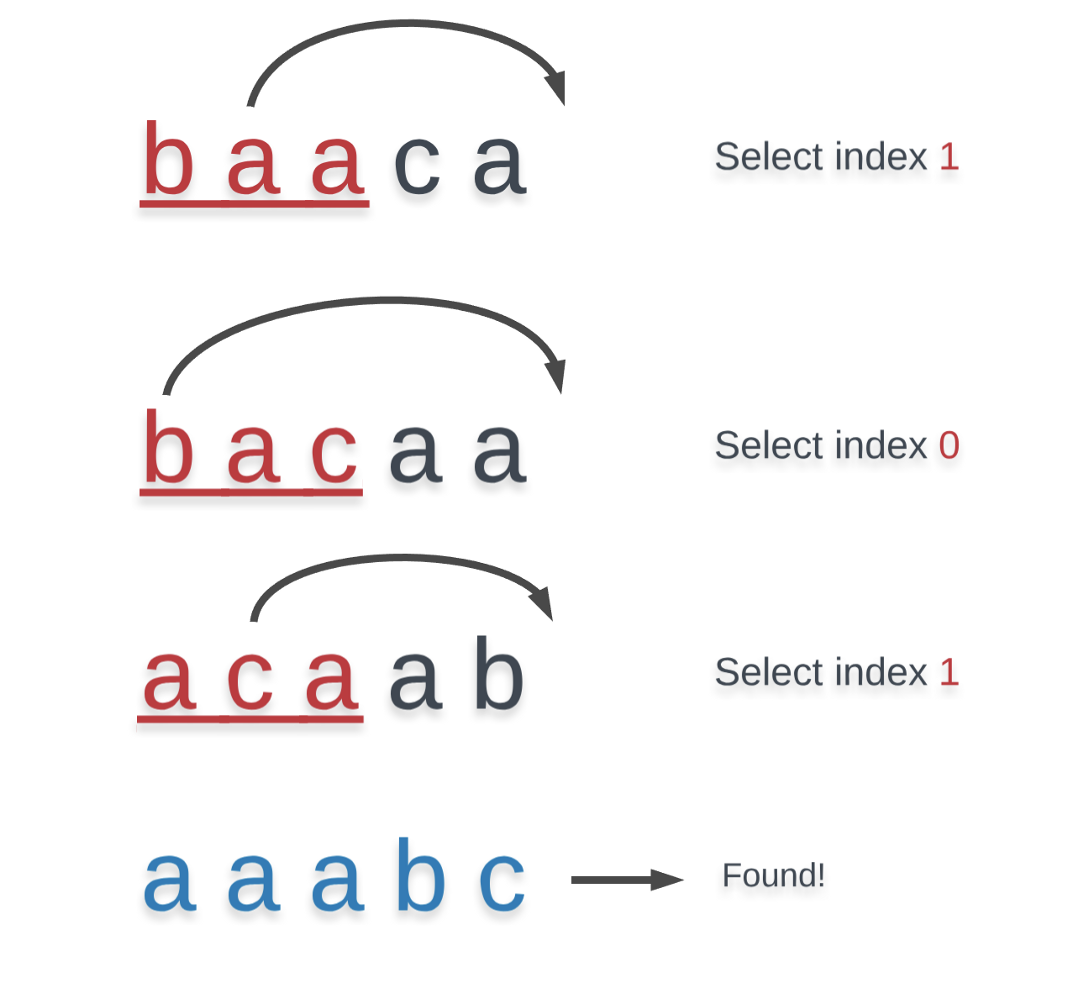
با فرض این که رشته مذکور کاراکترهای زیر را داشته باشد:

[a[0], a[1], a[2] … a[n-1

و بخواهیم یک موقعیت i (که i >= 0. i < n — 1) را با موقعیت i+1 تعویض کنیم یا [a[i را با [a[i+1 تعویض کنیم. می‌توان ادعا کرد که در مورد هر دو موقعیت همجوار در رشته می‌توان این حالت را با استفاده از چرخش روی رشته به دست آورد، یعنی فرض کنید رشته شامل 5 کاراکتر باشد و بخواهیم [a[2 و [a[3 را تعویض کنیم. در این حالت با چرخش آرایه زیر می‌توانیم به این حالت دست پیدا کنیم.

a[0], a[1], a[2], a[3], a[4], a[5] ROTATE around first element
a[1], a[2], a[3], a[4], a[5], a[0] ROTATE around first element
a[2], a[3], a[4], a[5], a[0], a[1] ROTATE around second element
a[2], a[4], a[5], a[0], a[1], a[3] ROTATE around first element
a[5], a[0], a[1], a[3], a[2], a[4] ROTATE around first element
a[0], a[1], a[3], a[2], a[4], a[5] ROTATE around first element

می‌توان با این ایده بیشتر کار کرد؛ اما ازلحاظ نظری می‌توان همه عناصر مجاور در یک رشته مفروض را با اجرای چندین چرخش به روش فوق با هم تعویض کرد. بدین ترتیب می‌توانیم نتیجه بگیریم از آن جا که می‌توان هر دو عنصر را تعویض کرد، پس می‌توان «مرتب‌سازی حبابی» (Bubble Sort) را نیز اجرا کرد.

الگوریتم مرتب‌سازی حبابی اساساً شامل مقایسه میان عناصر همجوار به منظور بالا/پایین کردن عناصر به موقعیت‌های متناظرشان در آرایه است. بدین ترتیب ما در راه‌حل فوق موقعیت‌های [a[2 و [a[3 را بدون بر هم زدن ترتیب توزیع هیچ کاراکتر دیگری با هم تعویض می‌کنیم.

بنابراین اگر k>1 باشد، می‌توانیم الگوریتم مرتب‌سازی حبابی را با استفاده از چرخش‌ها اجرا کنیم و در نهایت با به دست آوردن کوچک‌ترین رشته از نظر الفبایی باعث شویم که رشته مورد نظر با ترتیب نزولی مرتب‌سازی شود.

زمانی که k=1 باشد چطور؟

در این حالت ما آزادی زیادی در انتخاب این که کدام عنصر را به پشت آرایه انتقال بدهیم نداریم. در این حالت باید به همه چرخش‌های ممکن رشته اصلی نگاه کنیم و آن را که کمترین ارزش را از نظر الفبایی دارد بازگردانیم.

فیلم آموزش آرایه ها در زبان برنامه نویسی C (رایگان) در فرادرس

کلیک کنید

اگر به خاطر داشته باشید، تعداد چرخش‌ها برای رشته‌ای با اندازه N برابر با N بود. بنابراین وقتی k=1 باشد، باید همه چرخش‌های آرایه را بررسی کنیم و کوچک‌ترین رشته از نظر الفبایی را به دست بیاوریم.

در پیاده‌سازی کد الگوریتم فوق می‌بینید که این راه‌حل تا چه حد کوتاه است:

class Solution(object):
    def orderlyQueue(self, S, K):
        if K == 1:
            L = len(S)
            S = 2*S
            return min(S[i:i+L] for i in range(L))
return "".join(sorted(S))

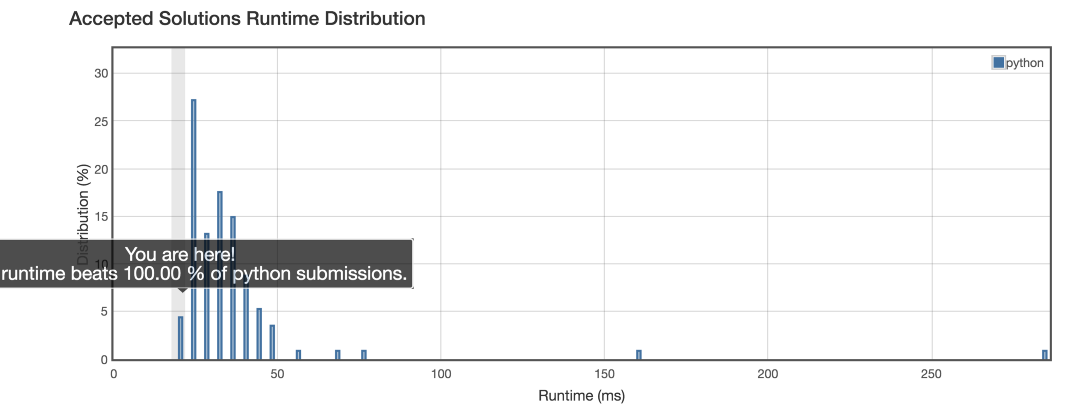
• پیچیدگی زمانی راه‌حل فوق برابر با (O(NLogN است، زیرا مشغول مرتب‌سازی رشته‌ای برای K>1 هستیم.
• پیچیدگی فضایی برابر با (O(N است چون اگر k=1 باشد، در این صورت باید S+S را ایجاد کنیم که تخصیص فضایی برابر با (O(N است.

بدین ترتیب به پایان این مقاله می‌رسیم. امیدواریم از این مقاله در مورد چرخش آرایه‌ها استفاده کرده باشید و بتوانید از مفاهیم مطرح شده در این مقاله به بهترین نحو استفاده کنید.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های برنامه‌‌نویسی
• آموزش ساختمان داده ها
• مجموعه آموزش‌های مهندسی نرم افزار
• معرفی مبانی ساختار داده و آرایه های داده ای — به زبان ساده
• آموزش پیشرفته ساختمان داده
• آرایه‌ ها در زبان برنامه نویسی سوئیفت (Swift) — به زبان ساده
• آموزش آرایه در ساختمان داده

==