درخت AVL – به زبان ساده
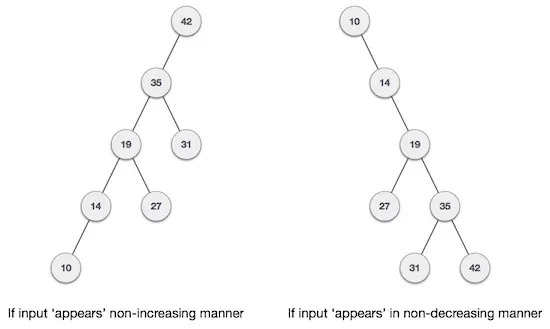
اگر ورودی یک درخت جستجوی باینری به روشی مرتب باشد (نزولی یا صعودی) در این صورت ظاهری شبیه زیر خواهد داشت:
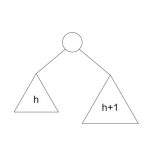
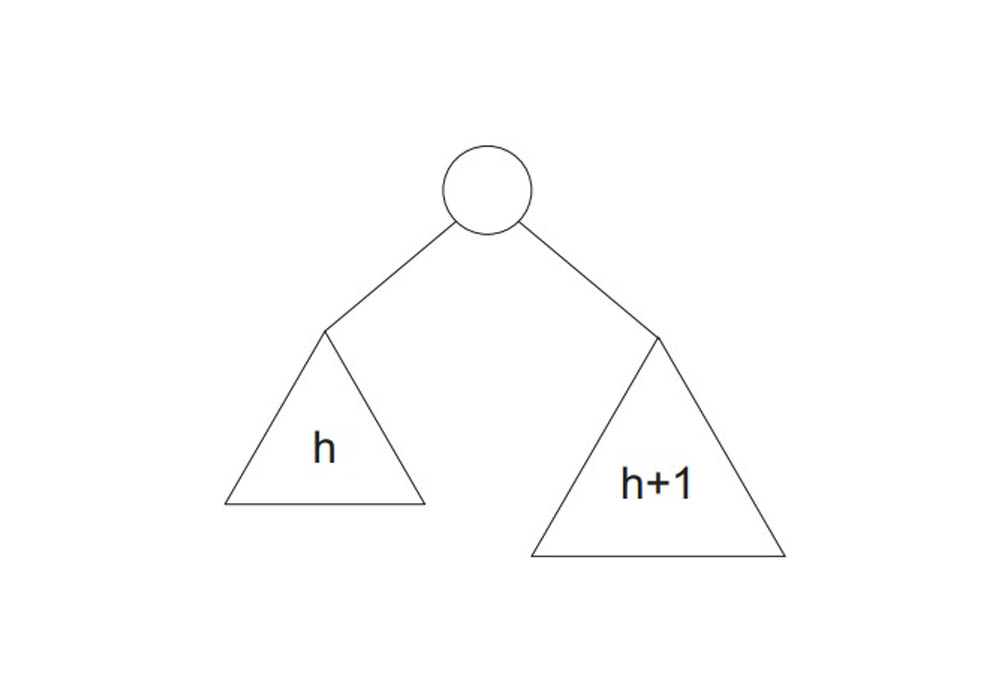
مشخص شده است که عملکرد سناریوی بدترین حالت برای درخت جستجوی باینری نزدیک به الگوریتمهای جستجوی خطی است که همان (O(n است. در مورد دادههای همزمان نمیتوان الگوی دادهها و فراوانیهای آنها را پیشبینی کرد. بنابراین باید درختهای جستجوی باینری موجود مجدداً متعادلسازی شوند.
درختهای AVL که به نام خالقانشان Adelson, Velski و Landis نامگذاری شدهاند، نوعی از درختان جستجوی باینری با ارتفاع متعادل هستند. درخت AVL سمت راست و چپ را بررسی کرده و تضمین میکند که زیردرخت راست و چپ اختلافی بیشتر از 1 واحد ندارند. این اختلاف به نام عامل تعادل (Balance Factor) نامیده میشود.
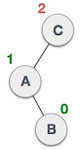
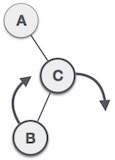
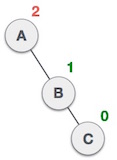
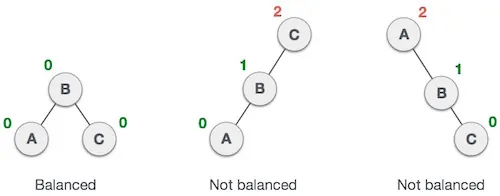
در ادامه میبینیم که درخت نخست متعادل است و دو درخت بعدی متعادل نیستند:
در مورد درخت دوم، زیردرخت چپ C ارتفاع 2 دارد و زیردرخت راست ارتفاع 0 دارد، بنابراین اختلاف برابر با 2 است. درخت سوم، زیردرخت راست A ارتفاع 2 دارد و زیردرخت چپ وجود ندارد و از این رو ارتفاعش 0 است و اختلاف بار دیگر 2 میشود. درخت AVL تنها امکان داشتن اختلاف (عامل تعادل) برابر با 1 را مجاز میشمارد.
ارتفاع زیردرخت راست - ارتفاع زیردرخت چپ = عامل تعادل
چرخشهای AVL
درخت AVL برای این که خود را متعادل کنند، باید چهار نوع چرخش زیرا را اجرا کند:
- چرخش چپ
- چرخش راست
- چرخش چپ-راست
- چرخش راست-چپ
دو نوع چرخش اول، چرخشهای منفرد هستند و دو نوع دوم چرخشهای دوگانه محسوب میشوند. برای این که درخت متعادل باشد، باید دستکم درختی با ارتفاع 2 گره داشته باشیم. در چنین درخت سادهای انواع مختلف چرخشها را بررسی میکنیم.
چرخش چپ
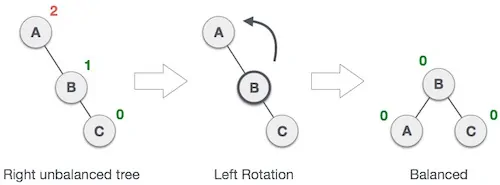
اگر درختی نامتعادل شود، وقتی گرهی در زیردرخت راستِ زیردرخت راست درج شود، در این صوت یک چرخش به چپ منفرد اجرا میشود:
در مثال فوق گره A نامتعادل است، زیرا به عنوان یک گره در زیردرخت راستِ زیردرخت راست A درج شده است. با اجرای چرخش چپ باعث میشویم که گره A به زیردرخت چپ گره B تبدیل شود.
چرخش راست
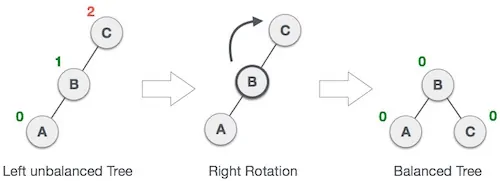
درخت AVL در صورتی که یک گره در زیردرخت چپِ زیردرخت چپ درج شود نیز میتواند نامتعادل شود. در این صورت باید چرخش راست روی درخت اجرا شود:
همان طور که در تصویر فوق مشخص است، گره نامتعادل با اجرای چرخش راست، به فرزند راستِ فرزند چپ خود تبدیل میشود.
چرخش چپ-راست
چرخشهای دوگانه نسخه پیچیدهتری از چرخشهای ساده هستند که در بخش قبلی بررسی کردیم. برای درک بهتر آنها باید به عملیاتی که در هر مرحله از چرخش اجرا میشود توجه کنیم. ابتدا شیوه اجرای چرخش چپ-راست را بررسی میکنیم. چرخش چپ-راست ترکیبی از چرخش چپ و سپس چرخش راست است.
| وضعیت | عمل |
|---|---|
 | یک گره در زیردرخت راستِ زیردرخت چپ ایجاد میشود. این امر موجب میشود که C یک گره نامتعادل شود. این سناریوها باعث میشوند که درخت AVL، چرخش چپ-راست را اجرا کند. |
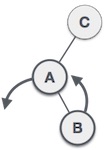 | ابتدا چرخش چپ روی زیردرخت چپ C اجرا میشود. این امر موجب میشود که A به زیردرخت چپ B تبدیل شود. |
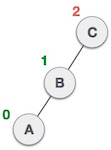 | با این وجود، گره C همچنان به دلیل وجود زیردرخت چپِ زیردرخت چپ نامتعادل است. |
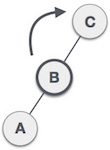 | اینک چرخش راست را روی درخت اجرا میکنیم و گره B را به یک ریشه جدید این زیردرخت تبدیل میکنیم. در این مرحله C به زیردرخت راستِ زیردرخت چپ خود تبدیل میشود. |
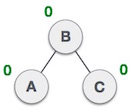 | اینک درخت در وضعیت متعادل قرار دارد. |
چرخش راست-چپ
نوع دوم از چرخشهای دوگانه، چرخش راست-چپ است. این چرخش ترکیبی از چرخش راست و سپس چرخش چپ است.
| وضعیت | عمل |
|---|---|
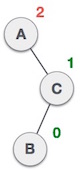 | یک گره در سمت چپ زیردرخت راست این زیردرخت درج شده است. این امر موجب شده است که A به یک گره نامتعادل با عامل تعادل 2 تبدیل شود. |
 | ابتدا چرخش راست را روی گره C اجرا میکنیم و آن را به زیردرخت راست ِ زیردرخت چپ خودش یعنی B تبدیل میکنیم. اینک B زیردرخت راست A شده است. |
 | گره A همچنان نامتعادل است و دلیل این مسئله زیردرخت راستِ زیردرخت راست آن است که به یک چرخش چپ نیاز دارد. |
 | یک چرخش چپ روی B اجرا میشود و آن را به گره ریشه زیردرخت تبدیل میکند. بدین ترتیب A به زیردرخت چپِ زیردرخت راست خودش (B) تبدیل میشود. |
 | اینک درخت متعادل شده است. |
بدین ترتیب این نوشته با موضوع معرفی درختهای AVL به پایان میرسد. هر گونه پیشنهاد یا دیدگاه خود را می توانید در بخش نظرات با ما و دیگر خوانندگان فرادرس در میان بگذارید.
اگر این نوشته مورد توجه قرار گرفته است، پیشنهاد میکنیم موارد زیر را نیز ملاحظه نمایید:
- مجموعه آموزشهای مهندسی نرم افزار
- آموزش پیشرفته ساختمان داده (همراه با حل نمونه سوالات کنکور ارشد و دکتری)
- ساختمان داده (Data Structure) — راهنمای جامع و کاربردی
- مهمترین الگوریتمهای یادگیری ماشین (به همراه کدهای پایتون و R) - جنگل تصادفی
- آموزش درخت جستجوی دودویی (AVL) در ساختمان داده ها
- مجموعه آموزشهای علوم کامپیوتر
==













سلام با تشکر از مطالب ، تیتر قسمت چرخش راست چپ دوبار تکرار شده
با سلام و احترام؛
سپاس از دقت نظر شما، این مورد اصلاح شد.
از همراهی شما با مجله فرادرس سپاسگزاریم.
عالی بود.استفاده بردم