تشخیص لبه در پردازش تصویر – به زبان ساده + کد پایتون

پردازش تصویر فرایندی است که از داده‌های تصویر برای استخراج اطلاعات استفاده می‌کند. الگوریتم‌های پردازش تصویر به دلیل حجم زیاد داده‌ها و اندازه بزرگ تصاویر ممکن است مدت زمان زیادی را صرف پردازش داده‌‌ها کنند. بنابراین، می‌توان مقدار اطلاعاتی را که الگوریتم باید روی آن تمرکز کند، کاهش داد. گاهی اوقات این اطلاعات می‌توانند تنها محدود به لبه‌های تصاویر باشند. زیرا، لبه‌ها از مهم‌ترین ویژگی‌های مرتبط با تصاویر هستند و ساختار اصلی تصاویر از طریق لبه‌های آن شناسایی می‌شود. در این مطلب از مجله‌ی فرادرس، روش‌های تشخیص لبه در پردازش تصویر را توضیح می‌دهیم.

تشخیص لبه در پردازش تصویر

سیستم بینایی انسان به شدت بر اساس تشخیص لبه‌ها و تفاوت‌های شدت نور در تصاویر متکی است و بیشتر اوقات طرح پیرامونی اشیا کافی هستند تا آن شی را بشناسیم. بنابراین، سیستم‌های پردازش تصویر، به طور عمده از روش‌های تشخیص لبه استفاده می‌کنند. به طور کلی، لبه‌ها در تصاویر در نقاطی قرار دارند که تابع شدت روشنایی به طور ناگهانی تغییر می‌کند.

فیلم آموزش پردازش تصویر در متلب در فرادرس

کلیک کنید

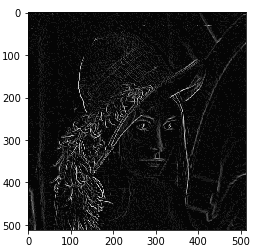
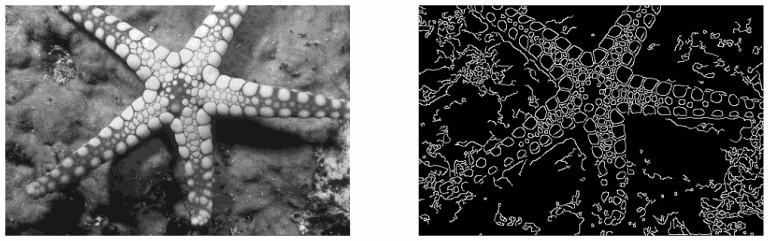
پس، اگر بخواهیم در تصاویر لبه‌ها را پیدا کنیم باید به دنبال محلی باشیم که شدت روشنایی در آن قسمت از تصویر تغییر ناگهانی می‌کند که نحوه سنجش تغییرات ناگهانی با استفاده از محاسبه مشتق امکان‌پذیر است. بنابراین، می‌توان لبه‌ها را با محاسبه مشتق تابع شدت روشنایی پیدا کرد. مثال زیر، تشخیص لبه تصویر یک ستاره دریایی با استفاده از الگوریتم‌های تشخیص لبه نشان می‌دهد.

همان‌طور که در تصویر بالا مشاهده می‌شود، لبه‌های ستاره دریایی در تصویر به خوبی مشخص شده‌اند. این به دلیل توانایی الگوریتم تشخیص لبه در شناسایی تغییرات ناگهانی در شدت روشنایی پیکسل‌ها است، که در این مورد، در مرزهای ستاره دریایی وجود دارد.تشخیص لبه به شناسایی تغییرات ناگهانی در تصویر نیاز دارد. این تغییرات توسط گرادیان‌ها نشان داده می‌شوند که تغییرات در میزان روشنایی پیکسل‌ها در جهات مختلف را نشان می‌دهند. با تشخیص گرادیان‌ها، می‌توان جهت و شیب تغییرات را مشخص کرد. گرادیان یک عملگر برداری است که با نماد ∇ نمایش داده می‌شود و جهت و شیب بیشترین نرخ تغییر یک تابع چندمتغیره را نشان می‌دهد.

در تصویر زیر مشاهده می‌کنید هنگامی که در جهت خط آبی‌رنگ حرکت می‌کنیم، هنگام برخورد با لبه، میزان روشنایی پیکسل‌ها به‌طور قابل‌توجهی تغییر می‌کند. برای مشخص کردن لبه‌های تصویر، شدت روشنایی هر پیکسل با پیکسل‌های اطرافش مقایسه می‌شود. نمودار سمت راست تصویر زیر، تغییرات شدت روشنایی پیکسل‌ها را در امتداد خط آبی‌رنگ نشان می‌دهد.به طور کلی، مشتق اول و مشتق دوم نمودار روشنایی می‌توانند برای بهبود دقت در مکان‌یابی نقاط لبه استفاده شوند.

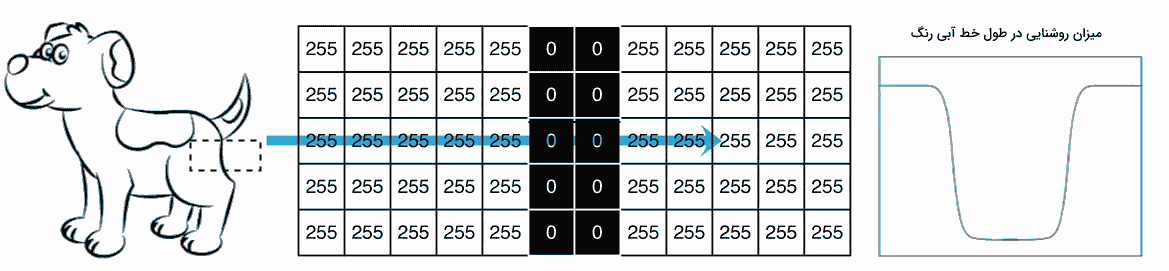
همان‌طور که گفتیم، محاسبه مشتقات اول و دوم تابع شدت روشنایی به ما کمک می‌کند تا نقاط لبه را با دقت بیشتری شناسایی کنیم. تصویر زیر نمودارهای مشتق اول و دوم را نشان می‌دهد که به خوبی این موضوع را تأیید می‌کنند.

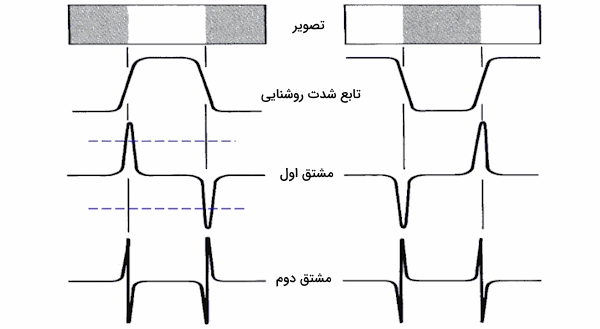
در روش تشخیص لبه با استفاده از مشتق اول، مکان لبه‌ها در نقاط اکسترمم محلی نمودار مشتق اول یافت می‌شوند. در روش تشخیص لبه با استفاده از مشتق دوم، لبه‌ها در مکانی تشخیص داده می‌شوند که تابع مشتق دوم از مقدار صفر عبور می‌کنند. تصاویر دنیای واقعی گرفته شده توسط دوربین‌ها، اغلب حاوی نویزهای تصادفی هستند که ممکن است بر کیفیت تصویر و دقت تحلیل تصاویر تأثیر منفی بگذارد. این نویزها را می‌توان در تابع روشنایی پیکسل‌های تصویر مشاهده کرد. در برخی موارد، این نویزها آن‌قدر زیاد هستند که با گرفتن مشتق اول تابع روشنایی، تشخیص لبه‌ها به صورت دقیق دشوار می‌شود.به عبارت دیگر، نویز می‌تواند تصویر را به گونه‌ای تحت تاثیر قرار دهد که تشخیص لبه‌ها دشوار شود. تصویر زیر تاثیرات نویز در نمودار مشتق اول را نشان می‌دهد.

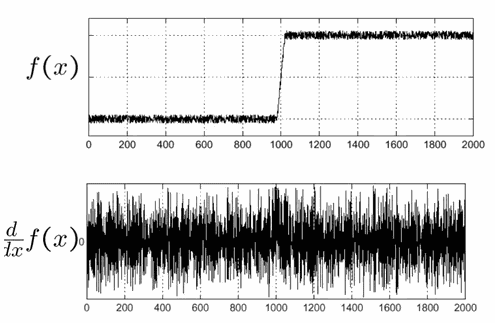
در نمودار بالا، کاملا مشخص است که نمی‌توان لبه‌های تصویر را با استفاده از پیدا کردن اکسترمم‌های محلی به دست‌آورد. بنابراین، لازم است که قبل از گرفتن مشتق تصویر آن را «هموارسازی» (Smoothing) کنیم تا رفع نویز شود. استفاده از فیلتر گاوسی یکی از روش‌های متداول برای هموارسازی تصاویر است. فیلتر گاوسی یک فیلتر پرکاربرد در پردازش تصویر است که از توزیع گاوسی برای کاهش نویز و هموار کردن تصویر استفاده می‌کند. این فیلتر نویزها و جزئیات ناخواسته را کاهش می‌دهد و عملکرد بسیاری از الگوریتم‌های پردازش تصویر را بهبود می‌بخشد.

اندازه کرنل فیلتر گاوسی یک پارامتر مهم است و تعیین می‌کند که چه مقدار از اطراف هر نقطه در تصویر باید در محاسبات فیلتر گاوسی لحاظ شود. با تنظیم اندازه فیلتر گاوسی، می‌توانید کنترل کنید که چه میزان از جزئیات تصویر حفظ شود و چه میزان از نویزها کاهش یابند. این تنظیم ممکن است بسته به نوع تصویر و هدف از پردازش تصویر، متغیر باشد. پس از اعمال فیلتر گاوسی پیداکردن اکسترمم‌های محلی و یا نقاط عبور از صفر به ترتیب در توابع مشتق اول و دوم آسان‌تر می‌شود.

به طور کلی، چندین روش برای تشخیص لبه وجود دارد که در ۳ رویکرد دسته‌بندی می‌شوند.

• رویکرد مبتنی بر گرادیان: روش‌های مبتنی بر گرادیان به طور معمول، شامل موارد زیر هستند.
  • عملگر Roberts
  • عملگرPrewitt
  • عملگر Sobel
  • الگوریتم Canny
• رویکرد مبتنی بر لاپلاسین: روش‌های مبتنی بر لاپلاسین یا مرتبه دوم در پردازش تصویر، معمولاً از گرادیان دوم یا لاپلاسین برای شناسایی لبه‌ها استفاده می‌کنند. یکی از عملگر‌های معروف که بر اساس لاپلاسین طراحی شده است، عملگر LOG (Laplacian of Gaussian) نام دارد که به منظور تشخیص لبه مورد استفاده قرار می‌گیرد.
• رویکرد مبتنی بر یادگیری عمیق: «شبکه‌های کانولوشن» (Convolution | CNN) یکی از معروف‌ترین معماری‌های یادگیری عمیق است که به منظور تشخیص لبه مورد استفاده قرار می‌گیرند.

در این مطلب از مجله فرادرس هر ۲ رویکرد مبتنی بر گرادیان و لاپلاسین را به تفصیل و به همراه نمونه کد پایتون بیان می‌کنیم. ما پیش‌تر مفهوم گرادیان را معرفی کردیم و گفتیم که برای محاسبه جهت و مقدار تغییرات روشنایی در یک نقطه از تصویر، از آن استفاده می‌کنیم. در این بخش کاملا با نحوه محاسبه گرادیان آشنا می‌شویم و سپس هر یک از روش‌های مبتنی بر گرادیان ذکر شده در بالا را شرح می‌دهیم.

نحوه محاسبه گرادیان در تصویر

استفاده از گرادیان تصویر در تشخیص لبه یکی از روش‌های متداول در پردازش تصویر است. گرادیان تصویر، جهت و مقدار تغییرات شدت روشنایی در یک تصویر را نشان می‌دهد. لبه‌ها در تصویر، نقاطی هستند که در آن‌ها گرادیان تصویر مقدار زیادی دارد. حال، به این موضوع می‌پردازیم که چگونه می‌توانیم گرادیان یک تصویر را به صورت دستی محاسبه کنیم. بیاییم تصویری با ابعاد ۳x۳ را در نظر بگیریم و سعی کنیم با استفاده از گرادیان تصویر، یک لبه پیدا کنیم. برای تشخیص وجود لبه، ابتدا یک نقطه را به عنوان پیکسل مرکزی را در نظر می‌گیریم. پیکسل مرکزی دارای ۴ همسایه اصلی به شرح زیر است.

فیلم آموزش کتابخانه Pillow برای پردازش تصویر در پایتون – مقدماتی در فرادرس

کلیک کنید

1. پیکسل بالا P(x, y-1)
2. پیکسل راست P(x+1,y)
3. پیکسل چپ P(x-1,y)
4. پیکسل پایین P(x,y+1)

در این روش، ابتدا اختلاف بین پیکسل‌های مقابل یکدیگر در تصویر، یعنی پیکسل بالایی، پایینی، چپ و راست محاسبه می‌شود.در صورتی که اختلاف بین پیکسل‌ها بزرگ باشد، نشان‌دهنده تغییر شدت روشنایی در آن ناحیه از تصویر است که ممکن است لبه باشد. در عبارات زیر پیکسل چپ، راست، بالا و پایین را به ترتیب با نمادهای PU، PR، PL و PB نشان می‌دهیم.

• تغییرات روشنایی در جهت X با محاسبه گرادیان در جهت افقی با استفاده از رابطه $$ PR - PL $$ به دست می‌آید.
• تغییرات روشنایی در جهت Y با محاسبه گرادیان در جهت عمودی با استفاده از رابطه $$ PB - PT $$ حاصل می‌شود.
• گرادیان تابع شدت روشنایی با استفاده از رابطه $$ ∇ f = [ ∂f/∂x , ∂f/∂y ] $$  محاسبه می‌شود.

در ادامه، برای یادگیری بهتر نحوه محاسبه گرادیان برای تصاویر، چند مثال بررسی می‌کنیم.

مثال اول

فرض کنید برای تصویر زیر قرار است گرادیان محاسبه کنیم.

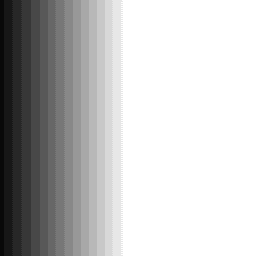
همانطور که مشاهده می‌شود، شدت روشنایی در این تصویر تنها در راستای افقی تغییر می‌کند. برای محاسبه بردار گرادیان، تصویر بالا را در یک تصویر ۳x۳ شبیه‌سازی می‌کنیم.

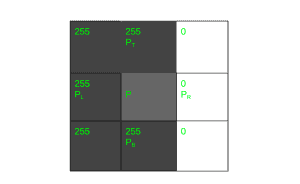
اکنون، بیاییم تغییرات سطح شدت روشنایی را برای تصویر بالا محاسبه کنیم.

$$ GX = PR - PL \\Gy = PB - PT \\GX = 0-255 = -255 \\Gy = 255 - 255 = 0 $$

بنابراین، گرادیان تابع روشنایی تصویر به صورت زیر نشان داده می‌شود.

 $$ ∇f = [ -255, 0] $$

مثال دوم

حال، مثالی دیگر را بررسی می‌کنیم که شدت روشنایی از بالا به پایین افزایش می‌یابد.

تصویر بالا را به تصویر ۳x۳ به صورت زیر تبدیل می‌کنیم.

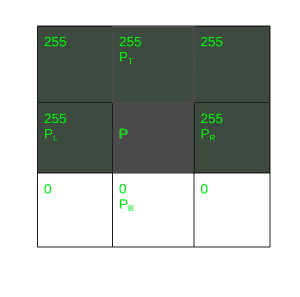
همانطور که مشاهده می‌شود، در جهت افقی تغییری در شدت روشنایی تصویر وجود ندارد. این بدان معناست که گرادیان تصویر در جهت افقی صفر است. گرادیان تصویر در جهت عمودی برابر با 255- است، زیرا شدت روشنایی از بالا به پایین افزایش می‌یابد. برای محاسبه گرادیان تصویر، از روابط زیر استفاده می‌شود.

$$ GX = PR - PL \\ Gy = PB - PT \\  GX = 255 - 255 = 0 \\ Gy = 0 - 255 = -255 $$

در نتیجه، گرادیان تابع روشنایی تصویر، برابر با بردار زیر است.

$$ ∇f= [0, -255] $$

مثال سوم

در مثال قبل، شدت روشنایی در جهت عمودی تغییر می‌کرد و در جهت افقی ثابت بود. اما در برخی تصاویر، شدت روشنایی در هر دو جهت افقی و عمودی تغییر می‌کند. در این حالت، برای محاسبه گرادیان تصویر باید تغییرات روشنایی را در هر دو جهت در نظر بگیریم.

تصویر ۳x۳ به صورت زیر نمایش داده می‌شود.

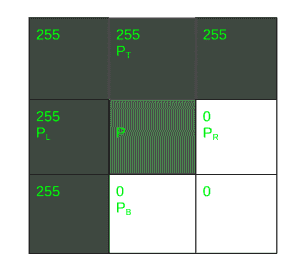
محاسبات زیر مقدار گردیان را برای این تصویر نشان می‌دهد.

$$ GX = PR - PL , Gy = PB - PT \\ GX = 0 - 255 = -255 \\ Gy = 0 - 255 = -255 $$

در این مثال، گرادیان تصویر به صورت زیر است که نشان می‌دهد مقدار تابع روشنایی تصویر به صورت افقی و عمودی به‌طور یکنواخت کاهش می‌یابد.

$$ 𝛥I = [ -255, -255] $$

اکنون که یاد گرفتیم چگونه مقادیر گرادیان را محاسبه کنیم، بد نیست با ۲ مفهوم مهم نیز آشنا بشویم.

• «اندازه گرادیان»(Gradient magnitude): اندازه گرادیان نشان‌دهنده میزان تغییر در شدت روشنایی است که با فرمول زیر محاسبه می‌شود.

   $$ M = \sqrt{\delta x^{2} + \delta y^{2} } $$

• «جهت گرادیان» (Gradient orientation): جهت گرادیان بیانگر جهت تغییر شدت روشنایی در تصویر است که می‌توانیم آن را با فرمول زیر محاسبه کنیم.

 $$ O = tan ^{-1} (\delta I/ \delta y) / (\delta I/ \delta X)) * (180/ \Pi) $$

جهت گرادیان نشان‌دهنده شیب تغییرات روشنایی است که بین 0 تا 180 درجه متغیر است. جهت گرادیان 0 درجه به آن معناست که تغییر روشنایی از چپ به راست و جهت گرادیان 90 درجه به معنای آن است که تغییر روشنایی از بالا به پایین است.

ما یاد گرفتیم که گرادیان‌ را به صورت دستی محاسبه کنیم، اما این کار برای تصاویر بزرگ به دلیل زمان‌بر بودن ابن محاسبات، امکان‌پذیر نیست. بنابراین، می‌توانیم گرادیان هر تصویر را با استفاده از اعمال فیلتر یا عملگری در سراسر تصویر به دست آوریم. در ادامه، چند فیلتر مبتنی بر گرادیان را به منظور عملیات لبه‌یابی یاد می‌گیریم. لازم به ذکر است که تمامی این فیلترها قابلیت تشخیص لبه‌های افقی و عمودی را دارند و تقریبا شبیه یکدیگر هستند، اما می‌توان گفت که در برخی ویژگی‌ها متفاوت هستند.

فیلتر‌های مبتنی بر گرادیان در پردازش تصویر

در پردازش تصویر، فیلترهای مبتنی بر گرادیان یکی از ابزارهای مهم هستند که برای استخراج ویژگی‌های تصویر به وسیلهٔ گرادیان - یا همان تفاضلات شدت روشنایی -استفاده می‌شوند. ما تا اینجا به طور کامل با نحوه محاسبه گرادیان در تصاویر آشنا شدیم. در ادامه، چند فیلتر مرسوم تشخیص لبه، Roberts و Prewitt و Sobel را مورد بررسی قرار می‌دهیم و در نهایت روش پیاده‌سازی را برای هر یک بیان می‌کنیم.

فیلم آموزش کتابخانه Pillow برای پردازش تصویر در پایتون – تکمیلی در فرادرس

کلیک کنید

فیلتر Roberts

فیلتر Roberts یک فیلتر ۲x۲ است که به عنوان یکی از قدیمی‌ترین و ساده‌ترین فیلترها شناخته می‌شود. این فیلتر یا همان کرنل، یک ماتریس کوچک است که هنگام اعمال از طریق کانولوشن بر روی تصویر، تفاوت بین پیکسل‌هایی که در موقعیت مجاور و در جهت مورب نسبت به یکدیگر واقع شده‌اند را محاسبه می‌کند که به همین دلیل می‌توانیم این نوع عملگر را فیلتر متقاطع بنامیم. ایده پشت عملگر Roberts این است که با جمع کردن مربع اختلافات بین پیکسل‌های مجاور در قطر پیکسل‌های تصویر، گرادیان را به صورت تقریبی محاسبه می‌کند. در ادامه، برای درک بهتر از نحوه دقیق محاسبه گرادیان با استفاده از فیلتر Roberts، یک مثال عملی را مورد بررسی قرار می‌دهیم.

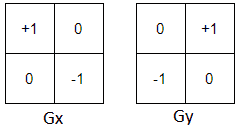
مثالی عملی از فیلتر Roberts

اکنون، در یک مثال عملی، به این می‌پردازیم که چگونه می‌توان گرادیان تصویر را با استفاده از فیلتر Roberts محاسبه کرد. در نظر بگیرید تصویری ۴x۴ مانند شکل زیر داریم.

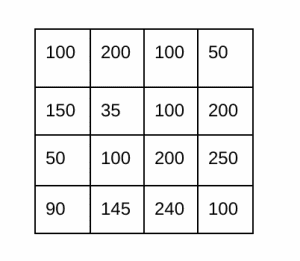
اکنون، فیلترهای Gx و Gy را در نظر می‌گیریم و آن‌ها را بر روی تصویر کانوالو می‌کنیم. حال، به محاسبات زیر نگاهی بیندازید.

برای این مثال، گرادیان در راستای Gx به صورت زیر محاسبه می‌شود.

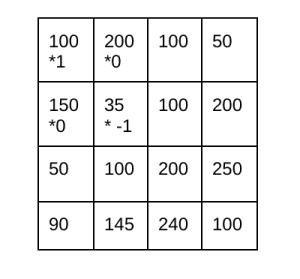
فرمول محاسبه نیز در زیر آورده شده است.

$$ Gx = 100 *1 + 200*0 + 150*0 - 35*1 \\ Gx = 65 $$

محاسبه‌ گرادیان در جهت Gy به این ترتیب، انجام می‌شود.

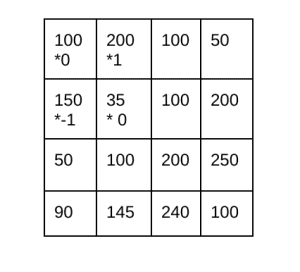
فرمول محاسبه نیز در زیر آورده شده است.

$$ Gy = 100 *0 + 200*1 - 150*1 + 35*0 \\ Gy = 50 $$

حالا که این دو مقدار را یافتیم، می‌توانیم اندازه و جهت گرادیان را با استفاده از محاسبات زیر به‌دست آوریم.

 $$  M = \sqrt{\bigtriangleup x^{2} + \bigtriangleup y^{2} } =  \sqrt{ 65^{2} + 50^{2} } ≅ 82 $$

همچنین، برای محاسبه جهت گرادیان می‌توان از تابع Arctan2 در کتابخانه NumPy به منظور به دست آوردن تانژانت معکوس و یا$$ tan⁻¹ $$ استفاده کرد. محاسبات زیر نحوه انجام این کار را نشان می‌دهد.

$$ O = tan ^{-1} (\delta I/ \delta y) / (\delta I/ \delta X)) * (180/ \Pi) = np.arctan2( Gy / Gx) * (180/ 𝝅) = 37.5685 $$

فیلتر Prewitt

فیلتر Prewitt یک ماتریس ۳x۳ است که نسبت به فیلترهای دیگر برای مثال Sobel که در بخش بعد به آن می‌پردازیم، حساسیت بیشتری به لبه‌های عمودی و افقی دارد. این فیلتر که دو نوع لبه - عمودی و افقی - را تشخیص می‌دهد با استفاده از کرنلی اختلافات شدت روشنایی پیکسل‌ها در جهت‌های مختلف را محاسبه می‌کند.

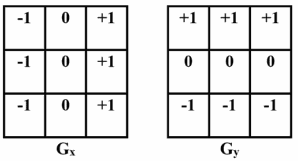
مثالی عملی از فیلتر Prewitt

حال، بیاییم گرادیان تصویر را با استفاده از کرنل Prewitt محاسبه کنیم. فرض کنیم که همان تصویر ۴x۴ قبلی را داریم.

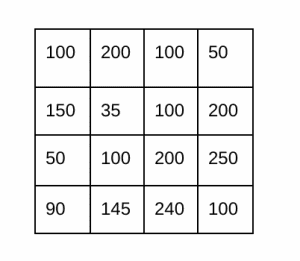
در ادامه، فیلترهای Gx و Gy را انتخاب و آن‌ها را بر روی تصویر اعمال می‌کنیم. سپس، نتایج را بررسی می‌کنیم.

گرادیان در راستای x به این صورت محاسبه می‌شود.

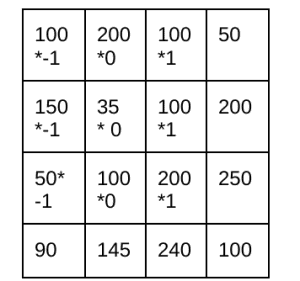
فرمول محاسبه نیز در زیر آورده شده است.

$$ Gx = 100 *(-1) + 200*0 + 100*1 + 150*(-1) + 35*0 + 100*1 + 50*(-1) + 100*0 + 200*1 \\ Gx = 100 $$

همچنین، برای محاسبه گرادیان در راستای y، محاسبات زیر را انجام می‌دهیم.

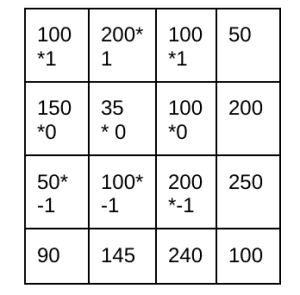
فرمول محاسبه نیز در زیر آورده شده است.

$$ Gy = 100 *1 + 200*1 + 200*1 + 150*0 + 35*0 +100*0 + 50*(-1) + 100*(-1) + 200*(-1) \\ Gy = 150 $$

حال، که هر دو این مقادیر را پیدا به دست آوردیم، به آسانی می‌توانیم اندازه و جهت گرادیان را محاسبه کنیم.

 $$  M = \sqrt{\bigtriangleup x^{2} + \bigtriangleup y^{2} } =  \sqrt{100^{2} + 150^{2} } = \sqrt{32500 }≅ 180 $$

با استفاده از مِتُد arctan2 در کتابخانه Numpy،‌ جهت گرادیان با استفاده کد زیر محاسبه می‌شود.

$$ O = np.arctan2( Gy / Gx) * (180/ 𝝅) = 56.3099 $$

فیلتر Sobel

فیلتر Sobel همانند فیلتر Prewitt است و تنها دو مقدار مرکزی از ۱ به ۲ و از ۱-‎‎ به ۲- در هر دو فیلتر مورد استفاده برای تشخیص لبه افقی و عمودی تغییر یافته‌اند. به عبارت دیگر، این دو فیلتر به یکدیگر شباهت دارند و تنها تفاوت آن‌ها در دو مقدار مرکزی است که با اختصاص دادن وزن بیشتری به ردیف مرکزی باعث افزایش حساسیت به تغییرات گرادیان در همان پیکسل مد نظر می‌شود.

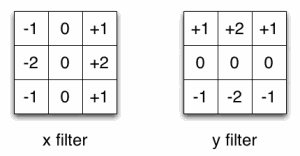
مثالی عملی از فیلتر Sobel

در این مثال عملی از روش تشخیص لبه با استفاده از فیلتر سوبل، فرض کنید که همان تصویر ۴x۴ مثال‌های قبل را داریم. سپس، با قرار دادن هر فیلتر روی تصویر و محاسبه جمع وزن‌دار مقادیر، به نتایج زیر می‌رسیم. برای محاسبه گرادیان در جهت x، فیلتر Gx را بر روی تصویر اعمال می‌کنیم. بنابراین، محاسبه گرادیان در جهت x به صورت زیر انجام می‌شود.

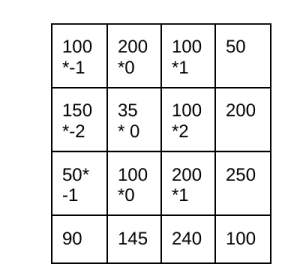
فرمول محاسبه نیز در زیر آورده شده است.

$$ Gx = 100 *(-1) + 200*0 + 100*1 + 150*(-2) + 35*0 + 100*2 + 50*(-1) + 100*0 + 200*1 \\ Gx = 50 $$

نحوه محاسبه گرادیان در راستای y را در ادامه آورده‌ایم.

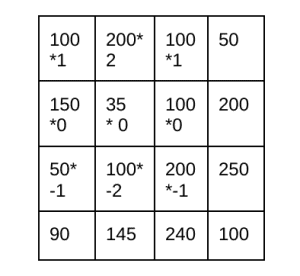
فرمول محاسبه نیز در زیر آورده شده است.

$$ Gy = 100 *1 + 200*2 + 100*1 + 150*0 + 35*0 +100*0 + 50*(-1) + 100*(-2) + 200*(-1) \\ Gy = 150 $$

در ادامه، اندازه و جهت گرادیان با استفاده از محاسبات زیر مشخص می‌شود.

$$ M = \sqrt{\bigtriangleup x^{2} + \bigtriangleup y^{2} } = \sqrt{50^{2} + 150^{2} } ≅ 58 $$

در قسمت زیر از مِتُد arctan2 در NumPy به منظور تعیین جهت گرادیان استفاده شده است.

$$ O = np.arctan2( Gy / Gx) * (180/ 𝝅) = 71.5650 $$

پیاده‌ سازی با استفاده از کتابخانه OpenCV

در این بخش از مجله فرادرس، به نحوه پیاده‌سازی الگوریتم‌های تشخیص لبه مبتنی بر گرادیان، می‌پردازیم. ابتدا لازم است کتابخانه OpenCV را نصب کنید.

فیلم آموزش مقدماتی پردازش تصویر با اپن سی وی OpenCV در پایتون Python در فرادرس

کلیک کنید

برای نصب این کتابخانه، دستورالعمل‌های زیر را دنبال کنید. کافی است که در محیط خط فرمان سیستم‌عامل خود دستور زیر را وارد کنید.

pip3 install opencv-python

python3 -c "import cv2"

پیاده‌ سازی عملگر Roberts

در این بخش، مثالی از اپراتور Roberts برای لبه‌یابی تصویر در محیط پیاده‌سازی ارائه دادیم. در قسمت زیر، گام‌های پیاده‌سازی کد به صورت خلاصه آورده شده است.

• گام اول: وارد کردن کتابخانه‌های مورد نیاز مانند OpenCV، NumPy و SciPy
• گام دوم: خواندن تصویر و تبدیل آن به مقیاس‌خاکستری
• گام سوم: مقداردهی اولیه به عملگرهای Roberts
• گام چهارم: اعمال فیلتر با استفاده از کانوالو کرنل به منظور محاسبه گرادیان تصویر
• گام پنجم: محاسبه اندازه گرادیان

1import cv2 
2import numpy as np 
3from scipy import ndimage 
4
5roberts_cross_v = np.array( [[1, 0 ], 
6							[0,-1 ]] ) 
7
8roberts_cross_h = np.array( [[ 0, 1 ], 
9							[ -1, 0 ]] ) 
10
11img = cv2.imread("input.webp",0).astype('float64') 
12img/=255.0
13vertical = ndimage.convolve( img, roberts_cross_v ) 
14horizontal = ndimage.convolve( img, roberts_cross_h ) 
15
16edged_img = np.sqrt( np.square(horizontal) + np.square(vertical)) 
17edged_img*=255
18cv2.imwrite("output.jpg",edged_img)

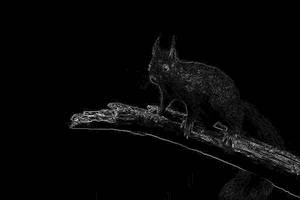
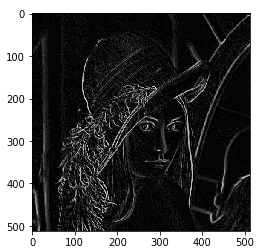
این مثال نشان دهنده یک فرآیند ساده از پردازش تصویر برای تشخیص لبه‌ها با استفاده از اپراتور Roberts است. در ادامه، ورودی و خروجی کد بالا را نمایش می‌دهیم. تصویر ورودی به شکل زیر در نظر گرفته شده است.

خروجی کد عملگر Roberts را می‌توانید در تصویر زیر مشاهده کنید.

پیاده‌ سازی عملگر Prewitt

در این بخش، نمونه پیاده‌سازی استفاده از اپراتور Prewitt برای تشخیص لبه در تصاویر ارائه شده است. در زیر، مراحل پیاده‌سازی کد به طور خلاصه توضیح داده شده است.

• گام اول: کتابخانه‌های مورد نیاز نظیر Numpy و CV2 وارد می‌شود.
• گام دوم: تصویر ورودی وارد و به مقیاس‌خاکستری تبدیل می‌شود.
• گام سوم: کرنل‌های Prewitt برای جهت‌های x و y ایجاد می‌شوند.
• گام چهارم: فیلتر Prewitt به تصویر در هر دو جهت اعمال می‌شود.
• گام پنجم: جذر جمع مربعات فیلترهای x و y محاسبه می‌شود.
• گام ششم: تصویر نهایی نمایش داده می‌شود.

1import cv2  
2import numpy as np 
3
4#Converting image to grayscale
5gray_img = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
6
7#Creating Prewitt filter
8kernelx = np.array([[1,1,1],[0,0,0],[-1,-1,-1]])
9kernely = np.array([[-1,0,1],[-1,0,1],[-1,0,1]])
10
11#Applying filter to the image in both x and y direction
12img_prewittx = cv2.filter2D(img, -1, kernelx)
13img_prewitty = cv2.filter2D(img, -1, kernely)
14
15# Taking root of squared sum(np.hypot) from both the direction and displaying the result
16prewitt = np.hypot(img_prewitty,img_prewittx)
17prewitt = prewitt[:,:,0]
18prewitt = prewitt.astype('int')
19plt.imshow(prewitt,cmap='gray'

کد بالا نشان می‌دهد که چگونه از اپراتور Prewitt برای تشخیص لبه‌ها در تصاویر استفاده کنیم. خروجی مربوط به کد فیلتر Prewitt را در قسمت زیر می‌توانید ملاحظه کنید.

پیاده‌ سازی عملگر Sobel

در این بخش، نمونه پیاده‌سازی تشخیص لبه با اپراتور Sobel ارائه شده است. مراحل پیاده‌سازی کد به طور خلاصه در زیر توضیح داده شده است.

• گام اول: کتابخانه‌های مورد نیاز وارد می‌شود.
• گام دوم: تصویر ورودی به فرمت خاکستری تبدیل می‌شود.
• گام سوم: کرنل‌های Sobel در جهت‌های x و y را تعریف می‌شود.
• گام چهارم: کرنل‌های تعریف شده در جهت‌های x و y اعمال می‌شوند.
• گام پنجم: اندازه گرادیان محاسبه می‌شود.
• گام ششم: تصویر نهایی نمایش داده می‌شود.

1import cv2
2import numpy as np
3import matplotlib.pyplot as plt
4
5# Load the image
6img = cv2.imread('your_image_path.jpg')  # Replace 'your_image_path.jpg' with the actual path to your image
7
8# Convert the image to grayscale
9gray_img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
10
11# Define Sobel kernels for x and y directions
12kernelx = np.array([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]])
13kernely = np.array([[1, 2, 1], [0, 0, 0], [-1, -2, -1]])
14
15# Apply Sobel filters in x and y directions
16img_x = cv2.filter2D(gray_img, -1, kernelx)
17img_y = cv2.filter2D(gray_img, -1, kernely)
18
19# Compute the gradient magnitude using the squared sum and taking the square root
20gradient_magnitude = np.hypot(img_x, img_y)
21
22# Display the result
23plt.imshow(gradient_magnitude.astype('int'), cmap='gray')
24plt.title('Sobel Operator Result')
25plt.show()

خروجی کد بالا را در قسمت زیر مشاهده می‌کنیم.

الگوریتم Canny در پردازش تصویر

تا اینجا، مفهوم گرادیان در تصویر و کاربرد آن در لبه‌یابی را آموختیم. گرادیان در تصویر یکی از مفاهیم پایه‌ای در حوزه پردازش تصویر است و در کاربرد لبه‌یابی با یافتن تغییرات شدت روشنایی بین پیکسل‌های تصویر، لبه‌ها را تشخیص می‌دهد. Roberts، Prewitt و Sobel از روش‌های مبتنی بر گرادیان به شمار می‌آیند که در این مطلب مورد بحث قرار گرفتند. مزایای اصلی این روش‌ها این است که ساده، سریع و آسان برای پیاده‌سازی هستند. روش‌های مبتنی بر گرادیانی که تا اینجا مورد مطالعه قرار دادیم نیز برخی مشکلات دارند، از جمله حساسیت به نویز که البته با اعمال فیلتری برای هموارسازی قبل از محاسبه گرادیان این مشکل تا حدی تعدیل می‌شود. از دیگر معایب این دسته از روش‌ها که می‌توان به آن‌ها اشاره کرد، تولید لبه‌هایی با عرض زیاد است که احتمال دارد بازنمایی دقیقی از لبه‌های واقعی نباشند. همچنین، این روش‌ها معمولا توانایی تشخیص لبه‌های نازک یا ظریف را ندارند.

فیلم آموزش پروژه محور بینایی ماشین با پایتورچ – تشخیص اشیا در PyTorch با پایگاه داده COCO در فرادرس

کلیک کنید

در ادامه مطلب، به معرفی الگوریتم Canny، یکی از الگوریتم‌های تشخیص لبه پرکاربرد و مفید در پردازش تصویر می‌پردازیم. این روش به دلیل توانایی آن در شناسایی لبه‌های نازک و دقیق و مقاومت در برابر نویز در روش‌های تشخیص لبه بسیار مورد استفاده قرار می‌گیرد. الگوریتم Canny شامل ۵ مرحله است که در ادامه به آن می‌پردازیم.

1. کاهش نویز
2. محاسبه گرادیان
3. «حذف نقاط غیر بیشنه» (Non-maximum suppression)
4. تعیین آستانه
5. دنبال کردن لبه‌های تصویر با روش «پسماند» (Hysteresis)

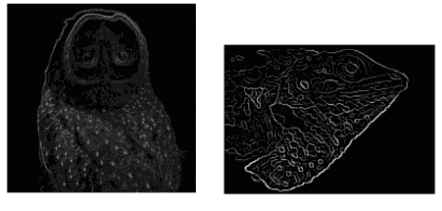
الگوریتم تشخیص لبه Canny ابتدا تصویر را با فیلتر گاوسی هموارسازی می‌کند تا میزان نویز را کاهش دهد. سپس، از فیلتر Sobel برای محاسبه جهت و شدت گرادیان در هر پیکسل تصویر استفاده می‌کند. در مرحله بعد، با استفاده از روش حذف نقاط غیر بیشنه پیکسل‌های غیر لبه را حذف می‌کند. در نهایت، با استفاده از ۲ مقدار آستانه، لبه های قوی و ضعیف را جدا می‌کند که لبه های ضعیف را با استفاده از روش Hysteresis حذف می‌کند. در ادامه، به صورت دقیق‌تری هر یک از ۵ گام الگوریتم را به ترتیب شرح می‌دهیم. تصاویر زیر را در هر مرحله از الگوریتم به کار می‌بریم تا نتایج را در هر گام به صورت شهودی مورد بررسی قرار بدهیم.

کاهش نویز

در این مرحله، تصویر را به حالت خاکستری تبدیل و از فیلتر گاوسی برای حذف نویز استفاده می‌کنیم. این کار به دلیل عدم وابستگی تشخیص لبه به رنگ اشیا انجام می‌شود. همچنین، تشخیص لبه در تصاویر حاوی نویز، چالش‌برانگیز و با مشکلاتی همراه است. نتایج حاصل از این مرحله در بخش زیر قابل ملاحظه است.

محاسبه گرادیان

حال، بر روی تصویر هموارسازی شده حاصل از مرحله قبل، به منظور محاسبه گرادیان پیکسل‌های تصویر، عملگر Sobel را در جهت‌های افقی و عمودی اعمال می‌شود. بنابراین، با توجه به آنچه پیش‌تر گفتیم به آسانی، زاویه و اندازه گرادیان محاسبه می‌شود.

حذف نقاط غیر بیشینه

با هدف اینکه لبه‌های شناسایی شده در تصویر نهایی نازک باشند، الگوریتم Canny یک سری از نقاط اضافی‌تر به عنوان لبه را حذف می‌کند. این عمل باعث حفظ نقاط لبه با گرادیان بیشینه - و حذف نقاط ضعیف‌تر و نویزی می‌شود، - که در نتیجه لبه‌های نازک و واضح‌تر در تصویر نهایی ایجاد می‌شود. روش کار به این صورت است که، مقدار هر پیکسل از تصویر با مقادیر مجاروش در جهت گرادیان مقایسه می‌شود. اگر در همان جهت گرادیان، مقدار پیکسلی از تمامی همسایگان بیشتر باشد، به عنوان «نقطه بیشینه محلی» شناسایی می‌شود. حال، به مثال ساده زیر توجه کنید.

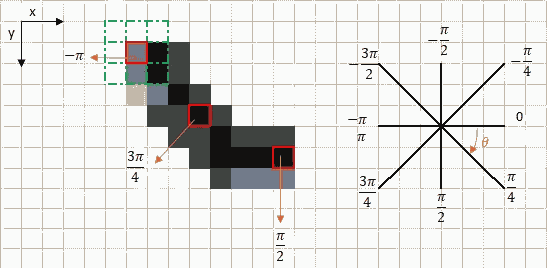
کادر قرمز در گوشه سمت چپ بالا، پیکسلی از تصویر شدت روشنایی را نشان می‌دهد که گرادیان شدت این پیکسل، با فیلتر گرادیان، مورد پردازش قرار گرفته است. جهت لبه مربوطه، با فلش نارنجی‌رنگ، با زاویه ۱۸۰- درجه یا منفی Π رادیان نشان داده شده است. این پیکسل را به صورت واضح‌تر در تصویر زیر نشان‌ داده‌ایم.

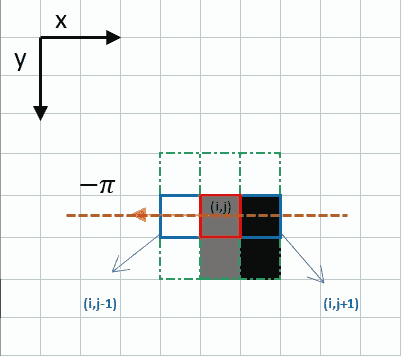
در تصویر بالا، جهت لبه با نقطه‌چین نارنجی رنگ مشخص شده است. هدف از این مرحله، بررسی این است که شدت پیکسل‌های هم‌جهت با لبه بیشتر یا کمتر از پیکسل پردازش شده، است یا خیر. به‌طور مثال، پیکسل (i, j) در تصویر بالا مورد پردازش قرار می‌گیرد. پیکسل‌های هم‌جهت با لبه شامل پیکسل‌های آبی‌رنگ (i, j-1) و (i, j+1) هستند. اگر شدت روشنایی یکی از این ۲ پیکسل، از پیکسل مرکزی - یا مورد پردازش - بیشتر باشد، پیکسل با شدت روشنایی بیشتر، انتخاب می‌شود. اگر هیچ‌یک از پیکسل‌های هم‌جهت با لبه شدت روشنایی بیشتری نداشته باشند، همان پیکسل مرکزی در نظر گرفته می‌شود. به بیان ساده‌تر، در این مرحله، الگوریتم Canny بررسی می‌کند که آیا در جهت لبه، پیکسل‌های با شدت روشنایی بیشتری وجود دارند یا خیر. اگر چنین باشد، شدت روشنایی پیکسل مرکزی یا مورد پردازش را به صفر می‌رساند، در غیر این صورت، پیکسل مرکزی به عنوان لبه در نظر گرفته و شدت روشنایی آن حفظ می‌شود. این مرحله برای حذف لبه‌های غیرمرتبط مانند لبه‌های ناشی از نویز یا عیوب تصویر، ضروری است.

بیاییم مثالی دیگری را بررسی کنیم.

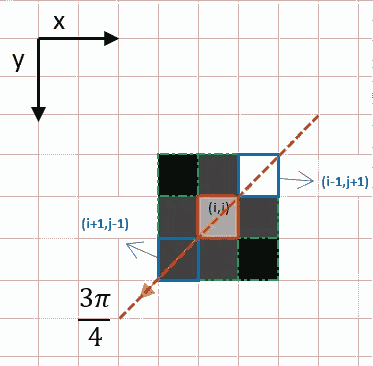
در این مثال، جهت خط نارنجی‌رنگ، مورب است. به عبارتی دیگر (i-1, j+1)، پیکسل‌هایی با بیشترین روشنایی هستند که در همین جهت قرار گرفته‌اند. مراحل حذف نقاط بیشینه برای این مثال هم همانند مثال قبل انجام می‌گیرد. در ادامه، به طور خلاصه مراحل حذف نقاط بیشینه را به صورت گام به گام بیان می‌کنیم، همچنین، پیاده‌سازی این مراحل را به زبان پایتون می‌آوریم.

• گام اول: یک ماتریس با همان اندازه کرنل گرادیان و با مقادیر اولیه صفر ایجاد کنید.
• گام دوم: بر اساس زاویه گرادیان، جهت لبه‌ها را شناسایی کنید.
• گام سوم: برای هر پیکسل در جهت مشخص شده، بررسی کنید که آیا شدت روشنایی پیکسل در همان جهت از شدت روشنایی پیکسلی که در حال، پردازش است بیشتر است یا خیر.
• گام چهارم: تصویر پردازش شده با الگوریتم «حذف نقاط بیشینه» (Non-Max Suppression) را برگردانید.

1def non_max_suppression(img, D):
2    M, N = img.shape
3    Z = np.zeros((M,N), dtype=np.int32)
4    angle = D * 180. / np.pi
5    angle[angle < 0] += 180
6
7    
8    for i in range(1,M-1):
9        for j in range(1,N-1):
10            try:
11                q = 255
12                r = 255
13                
14               #angle 0
15                if (0 <= angle[i,j] < 22.5) or (157.5 <= angle[i,j] <= 180):
16                    q = img[i, j+1]
17                    r = img[i, j-1]
18                #angle 45
19                elif (22.5 <= angle[i,j] < 67.5):
20                    q = img[i+1, j-1]
21                    r = img[i-1, j+1]
22                #angle 90
23                elif (67.5 <= angle[i,j] < 112.5):
24                    q = img[i+1, j]
25                    r = img[i-1, j]
26                #angle 135
27                elif (112.5 <= angle[i,j] < 157.5):
28                    q = img[i-1, j-1]
29                    r = img[i+1, j+1]
30
31                if (img[i,j] >= q) and (img[i,j] >= r):
32                    Z[i,j] = img[i,j]
33                else:
34                    Z[i,j] = 0
35
36            except IndexError as e:
37                pass
38    
39    return Z

پس از اعمال الگوریتم حذف نقاط بیشینه، تصویر خروجی به صورت زیر قابل مشاهده است.

تعیین آستانه

این مرحله با هدف شناسایی سه دسته پیکسل در تصویر حاصل از گام قبلی انجام می‌گیرد.

• پیکسل‌های قوی: شدت روشنایی این دسته پیکسل‌ها به میزانی بالا هست که به صورت قطعی به عنوان پیکسل‌های لبه در نظر گرفته شوند.
• پیکسل‌های ضعیف: شدت روشنایی این دسته از پیکسل‌ها به حدی زیاد نیست که به عنوان پیکسل‌های قوی شناخته شوند، اما به میزانی هم کم نیست تا به عنوان پیکسل‌های غیرمرتبط با لبه شناخته شوند.
• پیکسل‌های غیر مرتبط: این دسته از پیکسل‌ها به طور قطعی به عنوان پیکسل‌های غیر مرتبط با لبه شناسایی می‌شوند.

بنابراین، ۲ مقدار با نام‌های «آستانه بالا» و «آستانه پایین» تعریف می‌شوند. پیکسل‌هایی که گرادیانی بالاتر آستانه بالا داشته باشند در دسته پیکسل‌های قوی قرار می‌گیرند. پیکسل‌هایی با گرادیان پایین‌تر از‌ آستانه پایین به عنوان پیکسل‌های غیر مرتبط شناخته می‌شوند و به طور قطعی از نقاط لبه در نظر گرفته نمی‌شوند. حال، می‌توانیم بفهمیم که ۲ مقدار آستانه چه کاری انجام می‌دهند.

• «آستانه بالا» (High Threshold): این مقدار برای شناسایی پیکسل‌های قوی با شدت روشنایی بیشتر از آستانه بالا استفاده می‌شود.
• «آستانه پایین» (Low Threshold): این مقدار برای شناسایی پیکسل‌هایی مورد استفاده قرار می‌گیرد که شدت روشنایی آن‌ها کمتر از آستانه پایین است و به عنوان پیکسل‌های لبه‌ای در نظر گرفته نمی‌شوند.

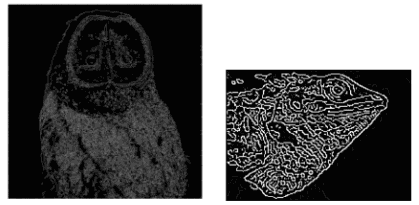
تمامی پیکسل‌هایی که شدت روشنایی آن‌ها بین دو مقدار آستانه بالا و پایین قرار می‌گیرند، به عنوان پیکسل‌های ضعیف یا احتمالی در نظر گرفته می‌شوند. مکانیسم Hysteresis که در مرحله بعدی به آن می‌پردازیم به ما کمک می‌کند تا نقاطی که ممکن است به عنوان پیکسل‌های قوی شناخته شوند و نقاطی که غیرمرتبط در نظر گرفته می‌شوند را از یکدیگر تشخیص دهیم. کد پایتون مرحله آستانه‌گذاری الگوریتم Canny به صورت زیر قابل پیاده‌سازی است.

1
2def threshold(img, lowThresholdRatio=0.05, highThresholdRatio=0.09):
3    
4    highThreshold = img.max() * highThresholdRatio;
5    lowThreshold = highThreshold * lowThresholdRatio;
6    
7    M, N = img.shape
8    res = np.zeros((M,N), dtype=np.int32)
9    
10    weak = np.int32(25)
11    strong = np.int32(255)
12    
13    strong_i, strong_j = np.where(img >= highThreshold)
14    zeros_i, zeros_j = np.where(img < lowThreshold)
15    
16    weak_i, weak_j = np.where((img <= highThreshold) & (img >= lowThreshold))
17    
18    res[strong_i, strong_j] = strong
19    res[weak_i, weak_j] = weak
20    
21    return (res, weak, strong)

خروجی حاصل از مرحله آستانه گذاری به صورت زیر قابل مشاهده است.

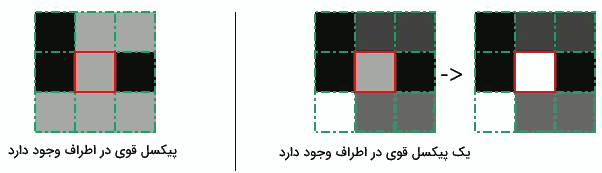
دنبال کردن لبه‌ های تصویر با روش Hysteresis

بر اساس نتایج به دست آمده از مرحله قبل، روش Hysteresis، تنها در صورتی پیکسل‌های ضعیف را به پیکسل‌های قوی تبدیل می‌کند که حداقل یکی از پیکسل‌های اطراف پیکسل مورد نظر، قوی باشد. تصویر زیر این روش را به خوبی بیان می‌کند.

کد پایتون زیر، این مرحله از الگوریتم را پیاده‌سازی می‌کند.

1def hysteresis(img, weak, strong=255):
2    M, N = img.shape  
3    for i in range(1, M-1):
4        for j in range(1, N-1):
5            if (img[i,j] == weak):
6                try:
7                    if ((img[i+1, j-1] == strong) or (img[i+1, j] == strong) or (img[i+1, j+1] == strong)
8                        or (img[i, j-1] == strong) or (img[i, j+1] == strong)
9                        or (img[i-1, j-1] == strong) or (img[i-1, j] == strong) or (img[i-1, j+1] == strong)):
10                        img[i, j] = strong
11                    else:
12                        img[i, j] = 0
13                except IndexError as e:
14                    pass
15    return img

خروجی حاصل از این مرحله به صورت زیر قابل مشاهده است.

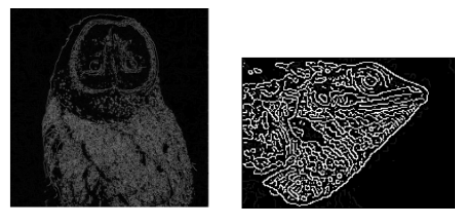
پیاده‌ سازی

تا اینجا با چند روش تشخیص لبه در پردازش تصویر آشنا شدیم. الگوریتم Canny یکی از بهترین روش‌های تشخیص لبه است که با هدف شناسایی لبه‌های نازک، دقیق‌تر و مقاومت بیشتر در برابر نویز نسبت به روش‌های تشخیص لبه قبلی طراحی شد. در بخش قبل مراحل اجرای این الگوریتم را گام به گام به صورت کامل، همراه با مثال شرح دادیم. در ادامه، کد پیاده‌سازی این الگوریتم را با استفاده از کتابخانه OpenCV در پایتون آورده‌ایم. همانطور که مشاهده می‌کنید، با استفاده از این کتابخانه، الگوریتم Canny تنها در چند خط کد قابل پیاده‌سازی است. ابتدا، گام‌های پیاده‌سازی کد به صورت خلاصه ارائه شده‌اند

• گام اول: کتابخانه‌های مورد نیاز مانند cv2 و matplotlib وارد می‌شوند.
• گام دوم: ابتدا تصویر خوانده و سپس به مقیاس خاکستری تبدیل می‌شود.
• گام سوم: به منظور کاهش نویز تصویر فیلتر گاوسی بر روی تصویر اعمال می‌شود.
• گام چهارم: الگوریتم تشخیص لبه Canny روی تصویر اجرا می‌شود.
• گام پنجم: تصویر خروجی نمایش داده می‌شود.

1import cv2
2import matplotlib.pyplot as plt
3img_path = 'starfish.png'
4image = cv2.imread(img_path)
5(H, W) = image.shape[:2]
6gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
7blurred = cv2.GaussianBlur(gray, (5, 5), 0)
8canny = cv2.Canny(blurred, 30, 150)
9fig, ax = plt.subplots(1, 2, figsize=(18, 18))
10ax[0].imshow(gray, cmap='gray')
11ax[1].imshow(canny, cmap='gray')
12ax[0].axis('off')
13ax[1].axis('off')
14plt.show()

تصویر زیر به ترتیب توصیر ورودی و خروجی کد پیاده‌سازی شده بالا را نمایش می‌دهد

رو‌ش‌ های مرتبه دوم

تمام روش‌های تشخیص لبه در پردازش تصویر که تا اینجای مطلب به آن پرداختیم، مشتقات مرتبه اول مقادیر پیکسل‌های تصویر را تقریب می‌زدند. بد نیست بدانیم که می‌توان از مشقات مرتبه دوم نیز، برای تشخیص لبه در پردازش تصویر استفاده کرد و پیش‌تر اشاره کردیم که نقاط لبه با استفاده از تابع مشتق دوم در نقاطی پیدا می‌شود که نمودار از صفر عبور می‌کند. یکی از عملگرهای بسیار پرکابرد که به منظور محاسبه لبه که در روش‌های مرتبه دوم مورد استفاده قرار می‌گیرد، «لاپلاسین»(Laplacian) نام دارد. به طور کلی، تابع لاپلاسین به صورت زیر تعریف می‌شود.

$$\triangledown ^{2}f(x, y) =\frac{\partial^2 f(x, y) }{\partial x^2} + \frac{\partial^2 f(x, y) }{\partial y^2} $$

فیلم آموزش پردازش تصویر در متلب در فرادرس

کلیک کنید

اگر از قسمت‌های قبل به یاد داشته باشید مقدار حاصل از رابطه گرادیان یک بردار بود اما همانطور که از رابطه بالا می‌توان دریافت کرد مقدار حاصل از رابطه لاپلاسین و یا مشتق دوم تنها یک مقدار اسکالر است. در حالت گسسته مشتق مرتبه دوم می‌تواند تفاضلی از تفاضل‌ها معنا دهد، بنابراین اگر بخواهیم تقریبی از لاپلاسین گسسته داشته باشیم می‌توانیم به رابطه زیر برسیم.

$$ \triangledown ^{2}f(x , y) =f(x + 1, y) + f(x - 1, y) + f(x, y + 1) + f(x, y - 1) - 4f(x , y) $$

فیلتر متناظر با رابطه لاپلاسین که در قسمت بالا معرفی کردیم به صورت زیر قابل مشاهده است.

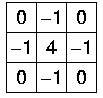
در رابطه لاپلاسین، (x , y) همان پیکسلی است که مرکز ماتریس کرنل بر روی آن قرار می‌گیرد. بنابراین همانطور که مشاهده می‌کنید ضریب نقطه مرکزی در فیلتر لاپلاسین معادل با مقدار ۴- است. به همین ترتیب ضرایب سلول‌های همسایه در ماتریس کرنل نیز با رابطه لاپلاسین مطابق هستند.

ماتریسی که در ادامه آورده‌ایم در روش‌های مبتنی بر لاپلاسین به عنوان عملگر نیز مورد استفاده قرار می‌گیرد. در این نوع کرنل، عناصر قطری هم لحاظ شده است.

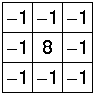
یکی از معایب تشخیص لبه با استفاده از فیلتر لاپلاسین مانند روش‌های گرادیان، حساس بودن به نویز است. بنابراین برای شناسایی لبه باید به نحوی نویز را از تصاویر حذف کرد. برای کاهش تأثیر نویز، معمولاً از روش‌های پیش‌‌پردازش مانند اعمال فیلترهای گاوسین یا سایر فیلترهای هموارسازی استفاده می‌شود. این فیلترها باعث کاهش نویز و حفظ لبه‌های واقعی در تصویر می‌شوند. تصویری که در ادامه آورده‌ایم به وضوح تأثیر نویز را در نتایج توابع گرادیان و لاپلاسین نشان می‌دهد.

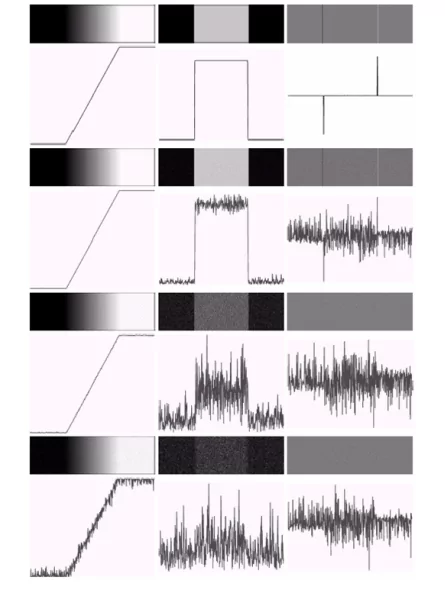
پس، می‌توان نتیجه گرفت که به هنگام استفاده از عملگرهای لبه باید نویز را رفع کنیم. یکی از روش‌های معمول برای رفع نویز در تصاویر شامل نویز، استفاده از فیلتر گاوسی به منظور هموارسازی تصویر است.به طور کل، فیلتر گاوسی یکی از روش‌های مرسوم در پیش‌پردازش داده‌های تصویری به شمار می‌آید. تصویر زیر فرایند کانوالو تصویر با استفاده از فیلتر گاوسی و سپس اعمال فیلتر گرادیان بر تصویر را به خوبی نشان می‌دهد.

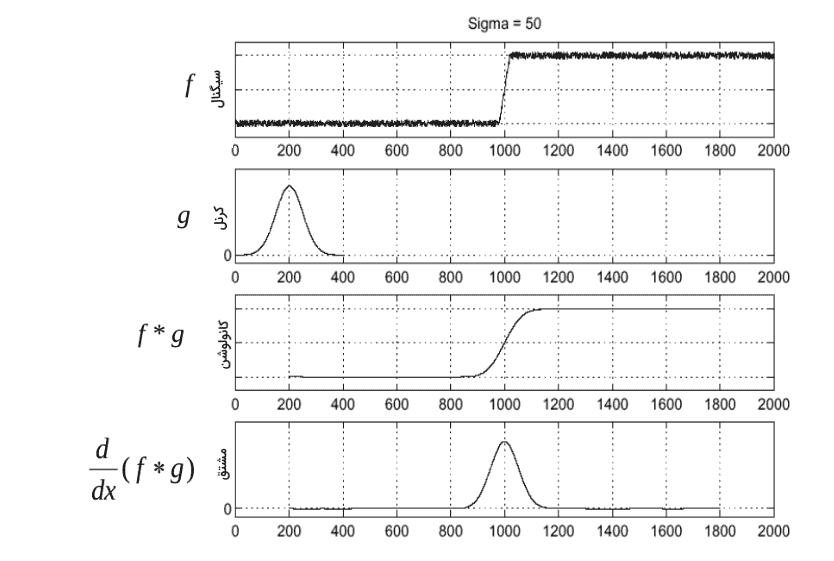
در تصویر بالا فرض شده است که تابع f شامل نویز است. در ادامه، این تابع با استفاده از کرنل گاوسی g هموارسازی می‌شود. خروجی عملیات کانولوشن این کرنل با تابع شامل نویز f، در ردیف سوم از تصویر نمایش داده شده است. همانطور که مشاهده می‌شود، تابع در این مرحله تا حد قابل قبولی هموارسازی شده است. در ادامه، فیلتر گرادیان به تصویر اعمال می‌شود تا مشتق تابع حاصل شود. حال، برای اینکه مراحل ذکر شده را به صورت کارامدتری انجام داد و تنها با اعمال یک فیلتر بتوان به همان نتیجه مورد نظر رسید، می‌توان عملیات انجام شده در بالا را در قالب رابطه‌ای نوشت و با استفاده از خاصیت شرکت پذیری عملگر کانولوشن، آن را بازنویسی کرد. معادله زیر را در نظر بگیرید.

$$ \frac{\mathrm{d} }{\mathrm{d} x}(f*g) = f*\frac{\mathrm{d} }{\mathrm{d} x}g $$

سمت راست این رابطه نشان‌دهنده یک عملیات کانوالو با فیلتر $$ \frac{\mathrm{d} }{\mathrm{d} x}g $$ بر روی تصویر اصلی $$ f $$ است. بنابراین می‌توانیم مراحل را ساده‌سازی کنیم، این‌بار مشتق فیلتر گاوسی محاسبه می‌شود و سپس با تصویر شامل نویز $$ f $$ کانوالو می‌شود. تصویر زیر این مراحل را به خوبی نشان می‌دهد.

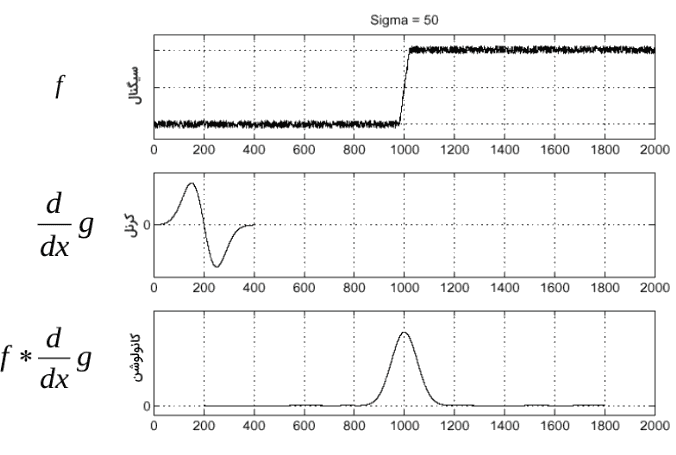
همانطور که پیش‌تر اشاره داشتیم محاسبه مشتق با استفاده از کانولوشن تصویر با فیلترهایی نظیر [1 -1] یا [1 0 -1] انجام‌پذیر است. بنابراین مشتق یک فیلتر گاوسی، حاصل کانولوشن فیلتری نظیر [1 -1] با فیلتر گاوسی g خواهد بود. تصویر زیر گویای این مطلب است.

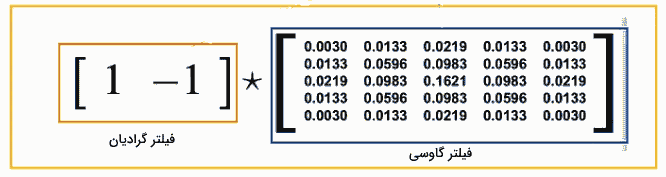
در این بخش، عملیات رفع نویز و لبه‌یابی با استفاده از گرادیان را تنها با اعمال یک کرنل به تصویر آموختیم. حال، لازم است بدانیم که موارد ذکر شده در بالا در فرایند تشخیص لبه با استفاده از فیلتر لاپلاسین نیز برقرار است. تنها کافی است که اینبار فیلتر لاپلاسین را جایگزین فیلتر گرادیان در حالت قبل کنیم. برای درک بهتر این موضوع، به روابط زیر توجه کنید. این روابط نشان می‌دهند که اگر تابع تصویر را با فیلتر گاوسی کانوالو کنیم که در اینجا تابع گاوسی با $$ h(x, y) $$ نمایش داده شده است -و سپس از کل عبارت یا حاصل کانولوشن، مشتق دوم یا همان لاپلاسین بگیریم، می‌توان از خاصیت شرکت‌پذیری استفاده کرد و مشتق را به داخل عبارت برد.

$$ h (x , y) = \sigma^{2} e^{\frac{x^2 + y^2 }{ \sigma^2}} \\g_{s} (x , y) = f (x , y) *h(x , y) \\g(x , y) = \triangledown ^{2} g_{s}(x , y) = \triangledown ^{2} (f (x , y) *h(x , y)) $$

در این حالت، عبارت زیر به دست می‌آید که در اینجا $$ h(x, y) $$ همان فیلتر گاوسی و $$\triangledown^{2} $$ عملگر لاپلاسین است. در اینصورت فیلتر لاپلاسن گاوسین به عنوان عملگری برای تشخیص لبه در پردازش تصویر، مورد استفاده قرار می‌گیرد که هم کار رفع نویز می‌کند و هم عملیات لاپلاسین را انجام می‌دهد.

$$ g(x , y) = f (x , y) * (\triangledown ^{2} h(x , y) ) $$

در رابطه بالا، عبارت $$\triangledown^{2}h(x, y) $$  همان «لاپلاسین گاوسین» (  Laplasian Of Gaussian | LOG) است. اکنون، ببینیم که چگونه فیلتر LoG را محاسبه کنیم. رابطه ریاضی LoG را می‌توان به صورت زیر بیان کرد.

$$ LoG (x , y) = - \frac{1}{\pi \sigma^{4}}\left [ 1 - \frac{x^{2} + y^{2}}{2\sigma^{2}}\right ] e^{-\frac{x^{2} + y^{2}}{2\sigma^{2}}} $$

برای به‌دست آوردن فیلتر LoG، می‌توان وزن‌های آن را از معادله بالا برای انحراف معیاری معین، نمونه‌برداری کرد. ذکر این نکته ضروری است که دقت در انتخاب اندازه کرنل اهمیت زیادی دارد. برای مثال، اگر اندازه فیلتر LOG، کوچک انتخاب شود، تصویر حاصل ممکن است دارای نویز باشد و اگر از یک کرنل گاوسی بسیار بزرگ استفاده شود، ممکن است عملکرد روش، در مکان‌یابی لبه‌ها ضعیف باشد.

پیاده‌ سازی

اکنون، بیاییم پیاده‌سازی روش تشخیص لبه LoG را با یک نمونه کد پایتون یاد بگیریم. کتابخانهOpenCV در پایتون تابع داخلی Laplacian()   ‎را برای محاسبه لاپلاسین یک تصویر ارائه می‌دهد.

گام‌های تشخیص لبه در پردازش تصویر با استفاده از عملگر LoG به صورت خلاصه، به شرح زیر است.

1. برای اعمال LoG روی تصویر، دو روش معمول وجود دارد:
   • روش اول: در این روش، که شامل ۲ مرحله است، ابتدا یک فیلتر هموارساز گاوسی به منظور کاهش نویز بر روی تصویر اعمال می‌شود. سپس، فیلتر لاپلاسین به تصویر اعمال می‌شود تا لبه‌ها را شناسایی کند.
   • روش دوم: این روش شامل یک مرحله است و در آن تصویر به طور مستقیم با یک کرنل LoG کانولو می‌شود که نحوه به دست آوردن فیلتر گاوسی را پیش‌تر به تفصیل بیان کردیم.
2. در تصویر حاصل شده از مرحله قبل، «نقاط عبور از صفر» (Zero Crossings) پیدا می‌شود. نقاط عبور از صفر مکان‌هایی هستند که مقادیر تصویر از مثبت به منفی یا از منفی به مثبت تغییر می‌کنند.
3. برای نقاط عبور از صفر، آستانه‌ای تعیین کنید تا لبه‌های قوی استخراج شوند.

حال، بیاییم مراحل بیان شده در بالا را در کد زیر مرحله به مرحله بررسی کنیم.

1import cv2
2import numpy as np
3 
4# Load the image in greyscale
5img = cv2.imread('D:/downloads/clouds.jpg',0)
6 
7# Apply Gaussian Blur
8blur = cv2.GaussianBlur(img,(3,3),0)
9 
10# Apply Laplacian operator in some higher datatype
11laplacian = cv2.Laplacian(blur,cv2.CV_64F)

یکی از راه‌های پیدا کردن نقاط عبور از صفر این است که مطابق کد زیر، هر پیکسل را برای عبور از صفر بررسی کنیم.

1
2def Zero_crossing(image):
3    z_c_image = np.zeros(image.shape)
4    
5    # For each pixel, count the number of positive
6    # and negative pixels in the neighborhood
7    
8    for i in range(1, image.shape[0] - 1):
9        for j in range(1, image.shape[1] - 1):
10            negative_count = 0
11            positive_count = 0
12            neighbour = [image[i+1, j-1],image[i+1, j],image[i+1, j+1],image[i, j-1],image[i, j+1],image[i-1, j-1],image[i-1, j],image[i-1, j+1]]
13            d = max(neighbour)
14            e = min(neighbour)
15            for h in neighbour:
16                if h>0:
17                    positive_count += 1
18                elif h<0:
19                    negative_count += 1
20 
21 
22            # If both negative and positive values exist in 
23            # the pixel neighborhood, then that pixel is a 
24            # potential zero crossing
25            
26            z_c = ((negative_count > 0) and (positive_count > 0))
27            
28            # Change the pixel value with the maximum neighborhood
29            # difference with the pixel
30 
31            if z_c:
32                if image[i,j]>0:
33                    z_c_image[i, j] = image[i,j] + np.abs(e)
34                elif image[i,j]<0:
35                    z_c_image[i, j] = np.abs(image[i,j]) + d
36                
37    # Normalize and change datatype to 'uint8' (optional)
38    z_c_norm = z_c_image/z_c_image.max()*255
39    z_c_image = np.uint8(z_c_norm)
40 
41    return z_c_image

سوالات متداول

در این قسمت به سوالات متدوال پیرامون تشخیص لبه در پردازش تصویر می‌پردازیم.

فیلم آموزش پروژه محور پردازش تصویر با OpenCV در C++‎ - تشخیص چهره (رایگان) در فرادرس

کلیک کنید

 از چالش‌های اصلی تشخیص لبه در پردازش تصویر چیست؟

یکی از چالش‌های اصلی در الگوریتم‌های تشخیص لبه در پردازش تصویر، حساسیت آن‌ها به نویز موجود در تصویر است. نویز می‌تواند به دلایل مختلف مانند نور کم، فشرده‌سازی یا نقص سنسور ایجاد شود. وجود نویز در تصویر می‌تواند لبه‌های کاذب ایجاد کند یا لبه‌های واقعی را تار کند و بر دقت و کیفیت تشخیص لبه‌ها تأثیر بگذارد.

کاربردهای تشخیص لبه در پردازش تصویر چیست؟

تشخیص لبه کاربردهای زیادی در زمینه‌های مختلفی مانند بینایی کامپیوتر، یادگیری ماشین، تجزیه و تحلیل تصویر، شناسایی الگو، تصویربرداری پزشکی، سنجش از دور و هنر دارد. روش‌های تشخیص لبه در پردازش تصویر می‌توانند با پیدا کردن مرزها و اشکال در تصاویر، برای شناسایی اشیا و چهره‌ها در تصاویر استفاده شوند.

مزایای اصلی الگوریتم تشخیص لبه Canny چیست؟

الگوریتم Canny به دلیل توانایی در شناسایی لبه‌های نازک، دقیق و مقاومت در برابر نویز، یکی از الگوریتم‌های تشخیص لبه پرکاربرد و مفید در پردازش تصویر است.

جمع‌ بندی

در این مطلب از مجله فرادرس، ابتدا مفهوم تشخیص لبه و اهمیت آن در زمینه پردازش تصویر را بررسی کردیم. سپس، با مفهوم گرادیان آشنا شدیم که از مفاهیم پایه در الگوریتم‌ها و روش‌های تشخیص لبه به شمار می‌آیند. رویکرد‌هایی که تاکنون، در روش‌های تشخیص لبه مورد استفاده قرار گرفته‌اند، در ۳ دسته کلی رویکرد مبتنی بر گرادیان، مبتنی بر لاپلاسین و مبتنی بر یادگیری عمیق قرار می‌گیرند. در این مطلب، به تفصیل رویکرد‌های مبتنی بر گرادیان و مبتنی بر لاپلاسین را مورد بررسی قرار دادیم. بنابراین، عملگرهای پایه‌ای و مهم در رویکرد مبتنی بر گرادیان، نظیر Roberts، Sobel و Prewitt را توضیح دادیم و برای هر یک، چند مثال عملی ارائه کردیم. در ادامه، الگوریتم Canny را که از روش‌های مبتنی بر گرادیان محسوب می‌شوند را معرفی و مراحل گام به گام آن را توضیح دادیم. همچنین، مزیت‌های این الگوریتم نسبت به سایر روش‌های تشخیص لبه نظیر Sobel را بیان کردیم.

فیلم آموزش پردازش تصویر و بینایی ماشین با اپن سی وی OpenCV در فرادرس

کلیک کنید

پس از معرفی روش‌های مرتبه دوم تشخیص لبه، ضرورت اعمال روش‌های هموارسازی و رفع نویز را قبل از عملیات لبه‌یابی بررسی کردیم. این امر به دلیل حساسیت روش‌های مبتنی بر گرادیان و لاپلاسین به تصاویر شامل نویز است. در ادامه، فیلتر لاپلاسین گاوسین را معرفی و روش محاسبه آن را با ذکر جزئیات توضیح دادیم. به این ترتیب، با روش تشخیص لبه لاپلاسین گاوسین (LOG) آشنا شدیم که از روش‌های مبتنی بر لاپلاسین محسوب می‌شود. همچنین، تمامی روش‌ها و الگوریتم‌ها را به همراه نمونه کد پایتون و توضیح مراحل کلی آن‌ها ارائه کردیم.