مدل فریدمن، رابرتسون، واکر یا FRW | هر آنچه باید بدانید

در مطلب مدل‌های نسبیتی عالم در مورد دو مدل نسبیتی عالم یعنی مدل اینشتین و دوسیتر صحبت کردیم. در این مطلب قصد داریم مدل فریدمن، رابرتسون، واکر یا FRW را معرفی کنیم و جنبه‌های مختلف آن را مورد بررسی قرار دهیم. اگر به مباحث کیهان شناسی علاقه‌مند هستید خواندن این مطلب به شما پیشنهاد می‌شود.

مدل فریدمن، رابرتسون، واکر یا FRW

مدل فریدمن، رابرتسون، واکر را اولین بار الکساندر فریدمن معرفی کرد که ریاضیدانی روس بود و در دانشگاه سن پترزبورگ فعالیت می‌کرد. در سالهای 1922 و 1924 او دو مقاله مهم منتشر کرد که نشان می‌دادند مدل‌های اينشتين و دسیتر در واقع دو مورد خاص از طبقه بسیار بزرگتری از مدل‌های نسبیتی عالم هستند که تمام‌شان با معادلات میدانی نسبیت عام و اصل کیهان شناختی مطابقت دارند.

در کیهان شناسی مدرن اصل کیهان شناختی به این معنی است که توزیع فضایی ماده در جهان وقتی در مقیاس به اندازه کافی بزرگ مشاهده شود همگن و ایزوتروپیک است زیرا انتظار می‌رود نیروها به طور یکسان در کل جهان عمل کنند و بنابراین باید به گونه‌ای باشند که هیچ بی نظمی قابل مشاهده‌ای در ساختار مقیاس بزرگ در طول تکامل حوزه ماده که در ابتدا توسط انفجار ایجاد شده است وجود نداشته باشد. اصل کیهان شناسی به تعریف ناظر نیز بستگی دارد و شامل دو مفهوم قابل آزمایش است.

ناظر در اصل کیهان شناختی به معنای هر مشاهده‌گر در هر مکان از جهان است نه فقط هر مشاهده‌کننده انسانی در هر مکان بر روی زمین. بر اساس نظر محققین بر اساس اصل کیهان شناسی جهان باید برای هر کسی و هر کجا که باشد یکسان باشد.

الکساندر فریدمن در سن پترزبورگ متولد شد و تحصیلاتش را نیز در همین شهر انجام داد او در سال 1920 برای کار در آکادمی علوم سن‏ پترزبورگ به این شهر بازگشت. با آنکه او بیشتر با کارهایش در زمینه هواشناسی تئوری شناخته می‌شد، به نسبیت عام نیز علاقه‌مند شد و از نبوغ ریاضی خویش برای کاوش در نتایج کیهان شناختی این تئوری بهره برد. تحقیقات او منجر به فرمولی برای تعیین نحوه تغییر ضریب مقیاس یا (t)R در هستی همگن و ایزوتروپیک که به شکل یکنواخت از ماده پر شده است، گردید. این رابطه را به نام خود او یعنی فرمول فریدمن نام‌گذاری کرده‌‏اند.

پس از آن هوارد رابرتسون و آرتور واکر به طور مستقل راه‌هایی برای اصلاح و بهبود تشریح ریاضی این مدل‌ها و نیز اطمینان از عمومیت آن‌ها ارائه دادند. کارهای این سه نفر یعنی فریدمن، رابرتسون و واکر چارچوبی ریاضی شکل داد که امروزه هنگامی که در مدل‌های کیهان شناختی نسبیتی از هستی همگن و ایزوتروپیک یاد می‌شود می‌توان از آن‌ها بهره برد.

هوارد پرسی رابرتسون ریاضیدان و فیزیکدان آمریکایی که تخصصش در کاربرد نظریه نسبیت عام در موقعیت‌های واقعی بود. در سال 1929، رابرتسون با استفاده از استدلال‌های عمومی که به هیچ فرض خاصی در زمینه خصوصیات ماده وابستگی نداشت، موفق شد برای هر نوع هستی كه از حيث فضايی در تمام زمان‌ها همگن و ايزوتروپيک باشد، یک فرمول کلی برای جداکردن رخدادها در فضا-زمان به دست آورد که امروزه به این رابطه متریک FRW می‌گوییم.

نفر سومی که در توسعه مدل فریدمن، رابرتسون، واکر نقش داشت آرتور جئوفری واکر بود. او بیشتر عمر آکادمیک خود را در دانشگاه لیورپول سپری کرد. آقای واکر ابتدا به عنوان مدرس و سپس به عنوان پروفسور ریاضیات در این دانشگاه به تدریس پرداخت و فرمول او برای جداسازی رخدادها در هستی همگن و ایزوتروپیک در سال 1936 منتشر شد. فرمول او مبنایی نسبتاً متفاوت از کارهای قبلی رابرتسون داشته است.

متریک مدل فریدمن، رابرتسون، واکر

خصوصیات هندسی فضا-زمان در هر کدام از مدل‌های فریدمن، رابرتسون، واکر (این مدل‌ها را معمولاً به شکل خلاصه FRW می‌نامند) را می توان از رابطه زیر برای جدایی فضا-زمان ds از دو رخداد که مختصات آن‌ها به واسطه مقدار بی‌‏نهایت کوچک dx, dy, dz و dt متفاوت است و در فاصله r از منبع قرار گرفته‌اند به دست آورد.

$$(\mathrm{d} s)^{2}=\frac{[R(t)]^{2}}{\left(1+\frac{k r^{2}}{4}\right)^{2}}\left[(\mathrm{~d} x)^{2}+(\mathrm{d} y)^{2}+(\mathrm{d} z)^{2}\right]-c^{2}(\mathrm{~d} t)^{2}$$

فیلم آموزش مقدماتی نجوم – نجوم باستان تا کیهان شناسی در فرادرس

کلیک کنید

معادله بالا را گاهی با عنوان متریک مدل رابرتسون-واکر نیز می‌شناسند. ما از این رابطه در این مطلب استفاده نخواهیم کرد اما ذکر سه نکته در مورد آن ضروری است، اول آنکه این فرمول در واقع تعمیم یافته به فضا-زمان منحنی است که توضیح کاملی از خصوصیات هندسی فضا-زمان تخت ارائه می‌دهد. دوم آنکه این فرمول در بردارنده پارامتر خمیدگی یا $$k$$ است که به تشخیص خمیدگی فضا-زمان کمک می کند، همان طور که گفتیم $$k$$ می‌تواند مقادیر $$+1$$، $$0$$ یا $$-1$$ به خود بگیرد. سوم آن که در این فرمول ضریب مقیاس یا $$R(t)$$ وجود دارد که انبساط یا انقباض فضا را به عنوان تابعی از زمان توصیف می‌کند.

رابطه بالا در تمام مدل‌های FRW کاربرد دارد اما برای حل جزئیات هر مدل خاص، تعیین مقدار $$k$$ و نیز تعیین شکل دقیق $$R(t)$$ ضرورت دارد. در موردی که هستی به شکل یکنواخت با ماده بدون فشار و با چگالی $$\rho=0$$ پر شده است شکل $$R(t)$$ را می‌توان با حل معادله پیچیده‌ای که با نام معادله فریدمن شناخته می‌شود، تعیین کرد. این معادله مهم مقدار $$R$$ و سرعت تغییرات آن را به پارامتر خمیدگی یا $$k$$، چگالی کیهانی یا $$\rho$$ و ثابت کیهان شناختی یا $$\Lambda$$ مربوط می‌کند. ما به جزئیات حل این معادله نخواهیم پرداخت اما مقادیر متفاوت $$k$$ و $$\Lambda$$ می‌تواند به اشکال کاملاً متفاوت $$R(t)$$ منجر شود. این موارد به شکل شماتیک در تصویر (4) نمایش داده شده است.

مدل فریدمن، رابرتسون، واکر و معادله فریدمن

باتوجه به مباحث طرح شده در قسمت قبل مشخص است معادله فریدمن دارای بیشترین اهمیت در فرآیند مدل‌سازی کیهان شناختی است. این معادله شکل $$R(t)$$ را تعیین کرده و در نتیجه تاریخ تکاملی هستی مدل شده را تثبیت می‌کند. در واقع سرنوشت هستی با معادله فریدمن معین می‌شود و به همین دلیل است که بسیاری از کیهان شناسان این معادله را مهم‌ترین معادله در کیهان شناسی می‌دانند.

در این معادله از $$\dot{R}(t)$$ برای نشان دادن سرعت تغییر ضریب مقیاس یا همان $$R(t)$$ استفاده می‌شود و معادله به شکل زیر است:

$$\dot{R}^{2}=\frac{8 \pi G R^{2}}{3}\left(\rho+\frac{\Lambda c^{2}}{8 \pi G}\right)-k c^{2}$$

در معادله بالا می‌دانیم که $$R$$ و $$\rho$$ به زمان وابسته هستند و تنها برای راحت شدن شکل معادله به صورت بالا نوشته شده‌اند. همچنین در این معادله با داشتن مقادیر $$k$$ و $$\Lambda$$ می‌توان رفتار $$R$$ را مشخص کرد. هرچند برای به دست آوردن جزئیات دقیق، دانستن مقدار $$\rho$$ در چند زمان مشخص ضروری است. در واقع می‌توان نشان داد در هستی بدون فشار $$\rho(t)[R(t)]^{3}$$ مقدار ثابتی مانند $$D$$ دارد. بنابراین اطلاعات چگالی معمولاً با مشخص کردن مقدار این ثابت و جایگزین کردن $$\rho$$ با $$\frac{D}{R^{3}}$$ در معادله فریدمن به دست می‌آید.

توجه داشته باشید که در مورد مدل بحرانی که در آن $$k=0$$ و $$\Lambda=0$$ است معادله فریدمن به صورت زیر خواهد بود.

$$\dot{R}^{2}=\frac{8 \pi G R^{2}}{3}$$

با جایگزین کردن $$\rho$$ با $$\rho_{crit}$$ و در نظر گرفتن اینکه $$[H(t)]^{2}=\frac{\dot{R}^{2}}{R^{2}}$$ معادله بالا را می‌توان به صورت $$\rho_{crit}=\frac{3H^{2}(t)}{8\pi G}$$ بازنویسی کرد.

لازم به ذکر است كه بر مبنای فیزیک نیوتنی معادله فریدمن را می‌توان با در نظر گرفتن انرژی مجموع یک توزیع کروی در حال انبساط از کهکشان‌ها به دست آورد. در این حالت $$kc^{2}$$ به انرژی مجموع کره، $$\dot{R}^{2}$$ به انرژی جنبشی کره و عبارت در بردارنده G به انرژی پتانسیل گرانشی کره مربوط است. بر این اساس معادله فریدمن را گاهی معادله انرژی عالم نیز نامگذاری کرده‌‏اند.

حالت‌های متفاوت مدل فریدمن، رابرتسون، واکر

تصویر (4) در بردارنده مقادیر زیادی اطلاعات است و لازم است به دقت مورد بررسی قرار گیرد. نکته اول آن است که هر کدام از نمودارهای کوچک $$R-t$$ به مقادیر متفاوتی از پارامتر خمیدگی $$k$$ و ثابت کیهان شناختی $$\Lambda$$ مربوط است. برای هر مجموعه از مقادیر هر یک از نمودارهای کوچک، تاریخچه انبساط يا انقباض هستی همگن و ایزوتروپیکی که با ماده دارای فشار صفر پر شده است را نشان می‌دهد. برای مثال ستون سمت چپ (که با $$\Lambda<0$$ مشخص شده است) در بردارنده تمام حالاتی است که ثابت کیهان شناختی در آن‌ها کمتر از صفر است.

ردیف بالایی نمودارها مربوط به حالتی است که $$k=+1$$ است. هم چنین ردیف میانی به $$k=0$$ و ردیف پایانی به $$k=-1$$ مربوط است. در تمامی این سه مورد نمودارها مشابه هستند. $$R$$ در زمان $$t=0$$ برابر صفر است سپس تا یک مقدار ماکزیمم افزایش پیدا کرده و پس از یک زمان محدود دوباره به سمت صفر میل می‌کند. به عبارت دیگر تمام این مدل‌ها هستی‌هایی را تشریح می‌کنند که عمر محدودی دارند. در این حالت هستی ابتدا به بیشترین حد انبساط رسیده و سپس مجدداً منقبض می‌شود. یادآوری این نکته مهم است که مقدار $$R$$ ترسیم شده در این نمودارها در واقع نماینده مقیاس هستی است و نه شعاع آن و تنها در حالتی که $$k=+1$$ است و فضا حجم کلی محدودی دارد، مفهوم شعاع هستی یا شعاع عالم مصداق خواهد داشت.

در سایر موارد یعنی حالاتی که $$k=0$$ یا $$k=-1$$ است، فضا نامحدود است و لذا مفهوم شعاع کیهانی معنی نخواهد داشت. با یادآوری این نکته که $$R$$ ضریب مقیاس است و در واقع جابه‌جایی نقاط را در یک هستی یکنواخت معین می‌کند، دیگر عباراتی در مورد شعاع یا قطر هستی بی معنی خواهد بود.

ستون دوم در تصویر (4) بسیار جالب توجه است. این ستون در بردارنده مدل‌هایی است که ثابت کیهان شناختی در آنها صفر است یعنی $$\Lambda=0$$. تا این اواخر تصور بر این بوده که این مدل‌ها واقعی‌ترین مدل‌ها از عالم هستند که ما در آن زندگی می‌کنیم. در اولین مدل از این طبقه $$k=+1$$ است یعنی فضا محدود است و نمودار $$R-t$$ مربوط به آن بار دیگر چرخه‌ای از انبساط و انقباض با عمر محدود را نشان می‌دهد. در این مدل و سایر مدل‌هایی که در آن $$R$$ در زمان $$t=0$$ برابر صفر است، بخش اولیه گسترش هستی را با نام «انفجار بزرگ» (big bang) معرفی می‌کنند. همچنین فروپاشی که در انتهای دیگر چرخه رخ می‌دهد را نیز با عنوان «خردشدن بزرگ» (big crunch) می‌شناسند. در بین مدل‌هایی که در آن‌ها $$\Lambda=0$$ است و تمام‌شان با انفجار بزرگ آغاز می‌شوند تنها مدلی که در آن $$k=+1$$ است با خرد شدن به پایان می‌رسد. این مدل را مدل بسته نامگذاری کرده‌اند.

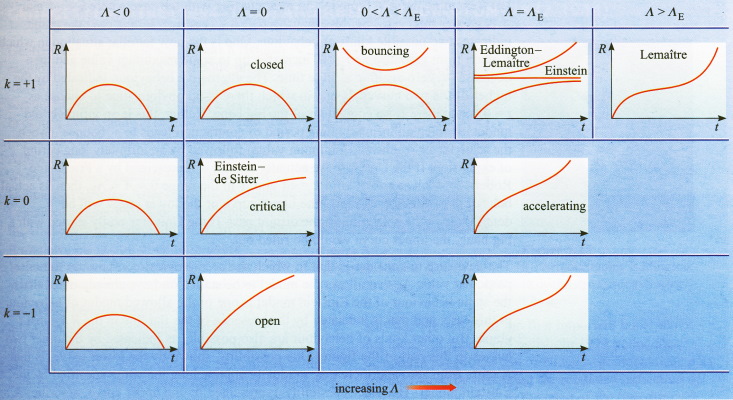
در دو مدل دیگری که در آن‌ها $$\Lambda=0$$ است فضا غیر محدود بوده و برای همیشه انبساط می‌یابد. مدلهایی که در آنها $$k=-1$$ است را مدل‌های باز نامگذاری می‌کنیم. در این مدل‌ها زمانی که $$t$$ به بی‌نهایت میل می‌کند رابطه بین $$R$$ و $$t$$ شکل ساده $$R\propto t$$ به خود می‌گیرد.

مدل‌هایی که در آن‌ها $$k=0$$ است حالت‌هایی مخصوص بین مدل‌های باز و بسته هستند. این مدل‌ها را به همین دلیل مدل‌های بحرانی نامگذاری می‌کنند. در این مدل‌ها رابطه بین $$R$$ و $$t$$ برای تمام مقادیر $$t$$ شکل $$R\propto t^{\frac{2}{3}}$$ به خود می‌گیرد. این مدل‌ها را با عنوان مدل‌های اينشتين- دسیتر نیز می‌شناسند هرچند هیچ گونه ارتباط مستقیمی به مدل اینشتین و مدل دسیتر ندارند. در تمام مدلهای باقی مانده دیگر تصویر (4)، ثابت کیهان شناختی بزرگتر از صفر است ($$\Lambda>0$$).

بهترین حالت آن است که تمام این مدل‌ها را در یک ستون منفرد در نظر گرفت هرچند هنگامی که $$k=+1$$ است درواقع چندین مورد کاملاً متفاوت برای بحث وجود خواهد داشت. بیش از آنکه به جزئیات هرکدام از مدل‌های فوق بپردازیم به پرسش زیر پاسخ دهید.

پرسش: (الف) در شکل (4) نمودار $$R-t$$ که مدل اينشتين را نشان می‌دهد تعیین کرده و مقادیر $$k$$ و $$\Lambda$$ مربوط به آن را بنویسید. (ب) آیا در این شکل نموداری مربوط به مدل دسیتر مشاهده می‌کنید؟

پاسخ: (الف) نمودار $$R-t$$ مربوط به مدل اینشتین خط صافی است که در وسط ردیف اول  نمایش داده شده است. بر اساس شکل (4) این نمودار معرف حالتی است که در آن $$k=+1$$ و $$\Lambda=\Lambda_{E}$$ است. توجه داشته باشید که $$\Lambda_{E}$$ به مقدار مخصوصی از ثابت کیهان شناختی مربوط است. این مقدار از معادله اینشتین به دست می‌آید که برای هستی ایستا با چگالی $$\rho$$ مقدار آن برابر با $$\Lambda_{E}=\frac{4\pi G\rho}{c^{2}}$$ است. (ب) نموداری که دقیقاً همانند مدل دسیتر برای عالم باشد در شکل (4) وجود ندارد. هرچند همانگونه که در ادامه خواهید دید مدل دسیتر در شکل (4) به عنوان یک حالت محدود از زمانی است که در آن $$\Lambda>0$$ و $$k=0$$ است.

بحث را با مدل‌هایی که در آن $$\Lambda>0$$ است ادامه می‌دهیم. در حالتی که $$k=+1$$ است و $$\Lambda$$ بزرگتر از صفر و كوچكتر از $$\Lambda_{E}$$ است یعنی ($$0<\Lambda<\Lambda_{E}$$)، نمودار دو نوع رفتار امکان‌پذیر از خود نشان می‌دهد. یکی حالتی است که حالا با آن آشنا هستیم یعنی حالتی که $$R$$ در زمان $$t=0$$ از مقدار صفر شروع شده تا مقدار ماکزیمم افزایش یافته و در یک زمان محدود مجدداً به سمت صفر میل می‌کند. اما رفتار دوم حالتی است که در آن زمان دقیقی برای انتخاب به عنوان $$t=0$$ نیست زیرا نقطه‌ای برای رویداد انفجار بزرگ وجود ندارد. بر خلاف حالت قبل در اين حالت دوره‌ای طولانی از انقباض عامل جهشی است (هنگامی که ضریب مقیاس به کمترين مقدار خود می‌رسد) که به دنبال دوره‌ه‏ای طولانی از انبساط حاصل شده است. اگر عالمی که ما در آن ساکن هستیم واقعاً از مدل فریدمن، رابرتسون، واکر در حالتی تبعیت کند که در آن $$k=+1$$ است و $$\Lambda$$ بین $$0<\Lambda<\Lambda_{E}$$ قرار گرفته است، آنگاه رفتار واقعی عالم چه زمانی که از منحنی بالایی و چه زمانی که از منحنی پائینی تبعیت کند، از رفتار آن در گذشته بسیار دور قابل تعیین و تعریف است و اگر هستی واقعاً با انفجار بزرگ آغاز شده باشد، نمودار بالایی این حالت قابل رد کردن است.

مورد بعدی که می‌توان در نظر گرفت حالتی است که در آن ثابت کیهان شناختی مقدار مخصوص $$\Lambda_{E}$$ دارد و این مقدار به مدل امکان ایستا بودن می‌دهد. پیش از این اشاره شد که رفتار ایستای مدل اينشتين یکی از رفتارهای مجاز در این نمودارها است و در نمودارهای $$R-t$$ به شکل خط صاف به نمایش درآمده است، اما گونه دیگری از رفتار نیز ممکن است. یک احتمال دیگر که توسط منحنی بالایی نشان داده شده است، هستی را در حالتی توصیف می‌کند که در شكلی بسیار نزدیک به حالت ایستا آغاز شده اما به میزان اندکی انبساط یافته است. حتی کمترین مقدار انبساط اولیه از این دست در نهایت به انبساطی دائمی منجر خواهد شد و این امکان را فراهم می‌آورد که هستی در حال انبساط زمان طولانی نامحدودی پیش از آنکه انبساط به شکل واقعی شروع به اثرگذاری کند این حالت یعنی انبساط نزدیک به حالت ایستا را داشته باشد. این امکان از نظر بسیاری از کیهان شناسان دارای جذابیت است.

رفتاری که شرح آن داده شد را با نام مدل «ادینگتون- لماتره» (Eddington-Lemaitre model) می‌شناسند. این مدل ابتدا در سال 1925 توسط جورج لماتره (1966 – 1894) که کشیشی بلژیکی بود معرفی شد اما در سال 1930 اختر فیزیکدان انگلیسی «سرآرتور ادینگتون» (1944 – 1882) در مقاله خود این مدل را به شکل کامل و جامع ارائه داد.

جورج لماتره علاوه بر کارهای برجسته روی مدل ادینگتون - لماتره به مدل‌هایی پرداخت که در آن‌ها $$k=+1$$ بوده و $$\Lambda$$ بزرگتر از $$\Lambda_{E}$$ بود این مدل‌ها را امروزه مدل لماتره نامگذاری کرده‌‏اند. لماتره دردهه 30 میلادی هنگامی که تعدادی از دانشمندان به منشاء عناصر شیمیایی یا به طور دقیق‌تر به منشاء هسته عناصر گوناگون علاقه‌مند شده بودند به دفاع از این مدل پرداخت. مدل لماتره هستی همگن و ایزوتروپیک را توصیف می‌کند که در آن فضا در هر زمان حجم کلی محدودی دارد و $$R$$ در زمان $$t=0$$ برابر صفر است و از اين نقطه آغاز می‌شود و بدون محدودیت افزایش می‌یابد. در این مدل انبساط از مرحله‌ای شبه استاتیک عبور می‌کند که در آن نمودار $$R-t$$ تقریباً صاف می‌شود و بنابراین حداقل برای مدت محدودی به هستی ایستا شباهت دارد، هرچند در واقعیت هرگز ایستا نیست.

لماتره چنین استدلال کرد که مراحل پایانی این مدل می‌تواند معرف هستی در حال انبساطی باشد که ما امروزه آن را مشاهده می‌کنیم. مراحل میانی زمان لازم برای تشکیل ستاره‌ها و کهکشان‌ها را ایجاد کرده و مراحل اولیه آن که حالتی بسیار متراکم، داغ و چگال داشته هسته برخی عناصر موجود در هستی را شکل داده است. هرچند بیشتر استدلال‌های لماتره امروزه رد شده‌اند اما اظهارات او در این زمینه که اولین هسته‌ها در عالم اولیه که بسیار متراکم، داغ و چگال بوده، شکل گرفته‌اند به شکل گسترده‌ای توسط ستاره‌شناسان پذیرفته شده است به همین دلیل نیز لماتره را فردی می‌دانند که اهمیت انفجار بزرگ را تشخیص داده هرچند او این واژه خاص را به کار نبرده است.

مدل فریدمن، رابرتسون، واکر و جرج لماتره و آرتور ادینگتون

جرج لماتره کیهان شناسی بلژیکی و در حین حال کشیش کلیسای کاتولیک بود. او ابتدا تحصیلاتش را در رشته مهندسی عمران انجام داد اما پس از خدمت در جنگ جهانی اول به مدرسه علوم دینی رفت و کشیش شد. او دست آخر نیز به تحصیل فیزیک در دانشگاه کمبریج پرداخت. در اینجا او با آرتور ادینگتون ملاقات کرد و پس ازسفرش به ایالات متحده با کارهای هابل و شاپلی آشنا شد. پس از بازگشت به بلژیک در سال 1927، لماتره در مقام پروفسور اختر فیزیک در دانشگاه لوین مشغول به کار شد. در سال 1931 لماتره افکار خود در زمینه اتم‌های اولیه فوق چگال را فرمول‌بندی کرد، اتم‌هایی که انفجار حاصل از آن‌ها انبساط در هستی را آغاز کرده بود.

سر آرتور ادینگتون تحصیلات خود در اختر فیزیک را در کمبریج انجام داد. او چندین تحقیق مهم روی ساختار ستاره‌ای به ويژه با تشخیص اهمیت فشار تابش در دوام (یا نابودی) تعادل انجام داده است. ادینگتون از حامیان تئوری نسبیت عام اينشتين بود و نویسنده اولین کتابی بود که در زمینه نسبیت عام در انگلستان انتشار یافت. در سال 1919 او سفری را برنامه ريزی كرد که منجر به تائید یکی از پیش بینی‌های تئوری نسبیت عام یعنی خمیدگی نور هنگام عبور از کنار اجرام سنگین شد.

در شکل (4) تنها یک نمودار معرف $$\Lambda>0$$ و $$k=0$$ است. تاکنون تصور بر این است که این مدل نزدیکترين مدل به هستی واقعی است. همچنین شواهد جدیدی از حرکات ستارگان و نجوم وجود دارد که مدل‌هایی که در آن‌ها $$k=0$$ را تائید می‌کند. همین شواهد میزان $$\Lambda$$ را نیز بزرگتر از صفر تخمین زده‌اند و به همین دلیل است که تصور می‌شود این مدل نزدیکترین حالت به هستی واقعی باشد. همانگونه که در نمودار $$R-t$$ نیز مشخص است این مدل هستی یکنواختی را توصیف می‌کند که با انفجار بزرگ آغاز شده و برای همیشه منبسط می‌شود. سرعت این انبساط مجدداً به شکل پیوسته افزایش می‌یابد و به همین دلیل این مدل را با عنوان مدل شتابدار نیز می‌شناسند.

نمودار آخر در شکل (4) مربوط به حالتی است که درآن $$k=-1$$ و $$\Lambda>0$$ است. در هستی یکنواختی از این دست، فضا نامحدود است و نوعی هندسه منحنی منفی دارد که سبب می‌شود مثلث‌های بزرگ کیهانی مجموع زوایای داخلی کمتر از 180 درجه داشته باشند. این مدل نیز با انفجار بزرگ آغاز می‌شود و مانند مدل شتابدار ضریب مقیاس آن از صفر شروع به افزایش کرده و به شکل موقت این رشد کاهش پیدا می‌کند و سپس مجدداً شتاب می‌گیرد.

تا اینجا در در مورد حالت‌های مختلف مدل فریدمن، رابرتسون، واکر بحث کردیم اما هنوز مدل دسیتر را در میان آنها پیدا نکرده‌ایم. این موضوع تا اندازه‌ای تعجب برانگیز است چرا که شکل (4) باید تمام مدل‌های همگن و ایزوتروپیک از هستی را که توسط مواد بدون فشار پرشده است را شامل شود. با این توصیف مدل دسیتر کجای این شکل قرار خواهد گرفت؟

در مدل دسیتر $$\Lambda>0$$ و $$k=0$$ است پس می‌توان انتظار داشت این مدل در بخشی که به مدل‌های شتابدار مربوط است قرار داشته باشد. در واقع این مدل نیز در همان جا قرار دارد اما تنها حالت محدودی از رفتاری که در این بخش از شکل تصویر شده است را ارائه می‌دهد. مدل دسیتر مقدار ماده قابل اغماضی دارد و بنابراین در آن $$\rho$$ و $$p$$ برابر صفر خواهند بود. در حالی که نمودار شکل (4) که مدل‌های $$\Lambda>0$$ و $$k=0$$ را شامل می‌شود حالت کلی‌تری را در شکل نشان می‌دهد که در آن ممکن است $$\rho$$ مقداری غیر از صفر داشته باشد، در این حالت چگالی ماده با زمان افزایش می‌یابد.

در این حالت هنگامی که $$t$$ افزایش می‌یابد ماده نیز در نهایت به شکل اندک گسترش خواهد یافت به گونه‌ای که چنین عالمی به ناچار مدل دسیتر خالی از خود نشان خواهد داد که در آن تنها ثابت کیهان شناختی باعث انبساط می‌شود.در نتیجه نمودار $$R-t$$ هنگامی که $$t$$ به بی نهایت میل کند به شکل دسیتر  نزدیک خواهد شد. بنابراین مدل دسیتر به شکل ضمنی در تصویر (4) قرار داده شده است.

پرسش: در زمینه حالت‌ها مختلف مدل فریدمن، رابرتسون، واکر یا FWR کدام مقادیر یا دامنه‌ها از پارامترهای $$k$$ و $$\Lambda به عالمی با مشخصات زیر مربوط هستند؟ الف) عالمی که نه همگن است و نه ایزوتروپیک ب) عالمی که در آن امکان انفجار بزرگ وجود ندارد ج) عالمی که انفجار بزرگ در آن ممکن است اما حداقل یک امکان دیگر نیز وجود دارد ($$\rho$$را بزرگتر از صفر فرض کنید) د) یک نقطه مشخص در فضایی که انفجار بزرگ در آن رخ داده است پس از سپری شدن مدت طولانی از این رویداد قابل تعیین است ف) در هر زمان خصوصیات هندسی مقیاس بزرگ فضا با خصوصیات فضای سه بعدی با هندسه تخت یکسان است ق) فضا حجمی محدود دارد و خطوط افقی که در ابتدا با یکدیگر موازی بوده‌‏اند ممکن است سرانجام به یکدیگر برسند. ی) انفجار بزرگ وجود داشته اما حجم فضا از زمان‌های اولیه غیر محدود بوده است‏. <b>پاسخ</b>: الف) تمام حالت‌های بررسی شده در تصویر (4) و در مدل فریدمن، رابرتسون، واکر شامل مدل‌های همگن و ایزوتروپیک از عالم هستند در نتیجه در این مدل‌ها عالمی با مشخصات حالت (الف) وجود ندارد. ب) در مدل فریدمن، رابرتسون، واکر تمام بازه‌های$$k$$و$$\Lambda$$شامل مدل‌هایی با انفجار بزرگ هستند اما مدل$$k=+1$$با$$0<\Lambda<\Lambda_{E}$$مدلی را توصیف می‌کند که انفجار بزرگ ندارد. حالتی که$$k=+1$$و$$\Lambda=\Lambda_{E}$$است، توصیف کننده یک عالم استاتیک و در نتیجه بدون انفجار بزرگ است یا می‌تواند غیراستاتیک و بدون انفجار بزرگ باشد. در میان حالت‌های محدود مانند حالت دوسیتر که چگالی صفر است حالت‌هایی وجود دارد که انفجار بزرگ در زمان‌های خیلی دور رخ داده است. ج) در مدل فریدمن، رابرتسون، واکر این حالت برای زمانی که$$k=+1$$و$$0<\Lambda<\Lambda_{E}$$رخ می‌دهد. د) در مدل فریدمن، رابرتسون، واکر هیچ محدوده‌ای وجود ندارد که اجازه دهد انفجار بزرگ با یک نقطه منحصر به فرد در فضا مرتبط شود. چنین ارتباطی اصل کیهان شناسی را نقض می‌کند. در حقیقت تصور غلط و گسترده‌ای وجود دارد که تصور می‌شود انفجار بزرگ در حقیقت انفجار اتمی متراکم است که در نقطه خاصی از فضا واقع شده است اما در واقع باید آن را به عنوان زمینه‌ای برای ایجاد فضا (یا بهتر بگوییم فضا-زمان) در نظر گرفت. ف) در مدل فریدمن، رابرتسون، واکر این حالت برای زمانی که$$k=0$$است صدق می‌کند. ق) در مدل فریدمن، رابرتسون، واکر این حالت برای زمانی که$$k=+1$$است صدق می‌کند. ی) در مدل فریدمن، رابرتسون، واکر این حالت برای تمام مدل‌هایی که در آن‌ها$$k=0$$یا$$-1$$است صادق است. در حقیقت با توجه به سرعت محدود نور هیچ مشاهده مستقیمی از قسمت‌هایی از عالم که از ما بسیار دور هستند به نوعی که نور از آنجا ساطع شده و به ما رسیده است وجود ندارد. جمع‌بندی در این مطلب به بررسی و معرفی مدل فریدمن، رابرتسون، واکر پرداختیم. در حقیقت مدل فریدمن، رابرتسون، واکر تمام حالت‌های همگن و ایزوتروپیک عالم را شامل می‌شود و با بررسی مقادیر مختلف$$k$$و$$\Lambda$$ حالت‌های مختلف و ممکن برای عالم را مورد بررسی قرار دادیم.