انتگرال قدر مطلق – توضیح به زبان ساده با مثال

قدرمطلق یکی از توابع مهم در ریاضی است که خروجی آن همیشه مثبت خواهد بود. قدرمطلق تابعی هست که باعث ناپیوستگی انتگرال در ریشه تابع می‌شود. در این مطلب از مجله فرادرس به معرفی تابع قدرمطلق می‌پردازیم و سپس روش محاسبه انتگرال قدرمطلق را ارائه می‌کنیم. برای محاسبه انتگرال قدرمطلق باید ابتدا تابع درون قدرمطلق را یکبار به ازای مقادیر مثبت و بار دیگر به ازای مقادیر منفی حساب کنید و انتگرال را براین اساس تفکیک کنید تا بتوانید قدرمطلق را از انتگرال حذف کنید. برای تکمیل این موضوع مثال‌های متنوع بررسی خواهیم کرد. اگر به این موضوع علاقه‌مند هستید این موضوع را تا آخر مطالعه کنید.

معرفی انتگرال

انتگرال ارتباط نزدیکی با مشتق دارد، در واقع انتگرال عکس مشتق به شمار می‌رود.

$$\int f'(x) dx = f(x) + c$$

در رابطه فوق c یک عدد ثابت است.

از لحاظ هندسی، با استفاده از انتگرال مساحت زیر منحنی را می‌توان محاسبه کرد در واقع انتگرال یک جمع پیوسته می‌تواند باشد.

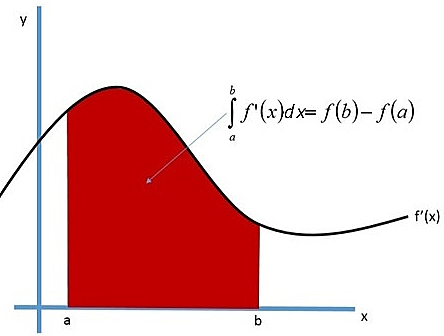
همان‌طور که مشاهده می‌کنید می‌توان مساحت اشکال پیچیده را با انتگرال محاسبه کرد.

انتگرال را می‌توان به دو گروه زیر دسته‌بندی کرد:

• معین
• نامعین

در انتگرال‌های معین کران‌ها یا حدود انتگرال مشخص است بنابراین پس از انتگرال گرفتن از تابع باید حدود را در آن جایگذاری کرد و از یکدیگر کسر کنیم. اما در انتگرال نامعین کران‌های انتگرال مشخص نشده‌اند درنتیجه پس از انتگرال گرفتن باید به پاسخ یک ‌c به عنوان عدد ثابت اضافه کنیم.

روش‌های حل انتگرال

روش‌های متنوع و جالبی برای حل انتگرال وجود دارد که رایج‌ترین آن‌ها عبارتند از:

os

• انتگرال با روش جایگزینی
• انتگرال با توان های sin و cos
• انتگرال با روش جایگزینی مثلثاتی
• انتگرال با روش جز به جز
• انتگرال توابع کسری

در مطلب انتگرال چیست از مجله فرادرس به طور کامل به شرح هر یک از این روش‌ها با مثال‌های متنوع پرداخته شده است.

انتگرال قدر مطلق

یکی از توابع ساده و کاربردی در ریاضیات و مهندسی قدرمطلق است که به صورت زیر تعریف می‌شود:

$$|x| = \begin{cases} x, & \text{if } x \geq 0 \\ -x, & \text{if } x < 0 \end{cases}$$

که به زبان ساده هر مقدار مثبت یا منفی که وارد تابع قدرمطلق شود خروجی آن با علامت مثبت خواهد بود.

انتگرال گرفتن از تابع قدرمطلق بسیار آسان است که برای انتگرال معین و نامعین شرح می‌دهیم.

انتگرال نامعین شامل تابع قدر مطلق

انتگرال نامعین که شامل تابع قدرمطلق است را باید یکبار برای مقادیر مثبت و یکبار برای مقادیر منفی حل کنیم بدین صورت که برای مقادیر مثبت کافی است تا علامت قدرمطلق را نادیده بگیریم و برای مقادیر منفی فقط باید یک منفی در کل عبارت ضرب کنیم بقیه مراحل حل انتگرال مانند سابق محاسبه می‌کنیم. برای درک بهتر این موضوع به مثال‌های زیر توجه کنید.

مثال اول انتگرال نامعین شامل قدر مطلق

می‌خواهیم انتگرال $$\int |x^3-5x^2+6x|dx$$ را حساب کنیم.

پاسخ:

در اینجا تابع داخل قدرمطلق یک چندجمله‌ای است. تابع داخل قدرمطلق را یکبار برای مثبت و یکبار برای منفی باید حساب کنیم.

$$\begin{cases}\frac{x^4}4-\frac{5x^3}{3}+3x^2+C & \Leftarrow& x^3-5x^2+6x\geq0\\\frac{x^4}4+\frac{5x^3}{3}-3x^2+C& \Leftarrow& x^3-5x^2+6x<0\end{cases}$$

مثال دوم انتگرال نامعین شامل قدر مطلق

انتگرال $$\int |\cos(x)|dx$$ را حساب کنید.

پاسخ:

در اینجا تابع داخل قدرمطلق، مثلثاتی است. تابع داخل قدرمطلق را یکبار برای مثبت و یکبار برای منفی حساب خواهیم کرد.

$$\begin{cases}\sin{(x)}+C & \Leftarrow& \cos{(x)}\geq0\\-\sin{(x)}+C& \Leftarrow& \cos{(x)}<0\end{cases}$$

مثال سوم انتگرال نامعین شامل قدر مطلق

می‌خواهیم انتگرال $$\int |1-e^{x-1}|dx$$ را حساب کنیم.

پاسخ:

در اینجا تابع داخل قدرمطلق، یک چندجمله‌ای با تابع نمایی است. تابع داخل قدرمطلق را یکبار برای مثبت و یکبار برای منفی حساب خواهیم کرد.

$$\begin{cases}x-e^{x-1}+C & \Leftarrow& 1-e^{x-1}\geq0\\-x+e^{x-1}+C& \Leftarrow& 1-e^{x-1}<0\end{cases}$$

مثال چهارم انتگرال نامعین شامل قدر مطلق

می‌خواهیم انتگرال $$\int |\log_3(x-1)|dx$$ را حساب کنیم.

پاسخ:

در اینجا تابع داخل قدرمطلق، یک تابع لگاریتمی است. تابع داخل قدرمطلق را یکبار برای مثبت و یکبار برای منفی باید حساب کنیم.

$$\begin{cases}\log_3{(x-1)\times(x-1)}-\frac{x-1}{\ln{3}}+C & \Leftarrow& \log_3(x-1)\geq0\\-\log_3{(x-1)\times(x-1)}+\frac{x-1}{\ln{3}}+C& \Leftarrow& \log_3(x-1)<0\end{cases}$$

مثال پنجم انتگرال نامعین شامل قدر مطلق

می‌خواهیم انتگرال $$\int_{} |x|-|x+1|dx$$ را حساب کنیم.

پاسخ:

در اینجا دو قدرمطلق داریم پس هر قدرمطلق را یکبار برای مثبت و یکبار برای منفی باید حساب کنیم.

برای مقادیر مثبت و مقادیر منفی هر کدام از قدرمطلق‌ها

$$\begin{cases}\int x-(-(x+1)) dx, x\geq0, x+1<0\\\int -x-(x+1)dx, x<0, x+1\geq0\\\int x-(-(x+1)) dx, x\geq0, x+1<0\\\int -x-(-(x+1))dx, x<0, x+1<0\end{cases}$$

عبارات را ساده‌سازی می‌کنیم:

$$\int -1dx, x\geq0, x+1\geq0$$

$$\int -2x-1dx, x<0, x+1\geq0$$

$$\int 2x+1 dx, x\geq0, x+1<0$$

$$\int 1dx, x<0, x+1<0$$

چون در این مثال دو قدرمطلق با توابع درونی مختلف داریم پس حدود هر کدام متفاوت است و باید اشتراک حدود را برای هر کدام جداگانه محاسبه کنیم مثلا برای مورد اول خواهیم داشت؛

$$x\geq0, x+1\geq0$$

$$x\geq0, x\geq-1$$

حدود مشترک برای مورد اول به صورت زیر است:

$$x\in [0, +\infty\rangle$$

همین فرآیند را برای بقیه نیز تکرار می‌کنیم. بنابراین حدود به شکل زیر است:

$$\int -1dx, x\in [0, +\infty\rangle$$

$$\int -2x-1dx, x\in[-1,0\rangle$$

$$\int 2x+1 dx, \emptyset$$

$$\int 1dx, x\in\langle-\infty,-1\rangle$$

مورد سوم که حدود متغیر در آن صفر است را حذف می‌کنیم بنابراین خواهیم داشت:

$$\int -1dx, x\in [0, +\infty\rangle$$

$$\int -2x-1dx, x\in[-1,0\rangle$$

$$\int 1dx, x\in\langle-\infty,-1\rangle$$

پس از انتگرال گرفتن از سه مورد فوق، جواب‌ها با محدوده هر یک به صورت زیر است:

$$-x+C , x\in [0, +\infty\rangle$$

$$-x^2-x+C , x\in[-1,0\rangle$$

$$x+C , x\in\langle-\infty,-1\rangle$$

مثال ششم انتگرال نامعین شامل قدر مطلق

انتگرال زیر که شامل تابع قدرمطلق هست را محاسبه کنید.

$$\int_{} |x|dx$$

پاسخ:

با استفاده از تعریف قدرمطلق تابع را به دو قسمت تفکیک می‌کنیم.

$$\begin{cases}\int_{} xdx, x\geq0\\\int_{} -xdx, x<0\end{cases}$$

منفی را از انتگرال دوم بیرون می‌آوریم.

$$-\int_{} xdx, x<0$$

بنابراین دو انتگرال فقط در یک ضریب منفی با یکدیگر اختلاف دارند. حل این انتگرال بسیار آسان است.

$$\int x dx=\frac{x^2}2+c$$

در نتیجه برای مقادیر مثبت و منفی خواهیم داشت:

$$\begin{cases}\frac{x^2}2+C & x\geq0\\-\frac{x^2}2+C & x < 0\end{cases} $$

مثال هفتم انتگرال نامعین شامل قدر مطلق

انتگرال $$\int_{}^{} \mid \cos \left( x \right) - \frac{3}{{{x^5}}}\mid \, dx$$ را محاسبه کنید.

پاسخ:

در این مثال، یک تابع مثلثاتی و یک تابع کسری درون قدرمطلق داریم. مانند مثال‌های قبل تابع داخل قدرمطلق را یکبار برای مثبت و یکبار برای منفی باید حساب کنیم.

 

$$\begin{cases}(\cos \left( x \right) - \frac{3}{{{x^5}}})&\Leftarrow& \cos \left( x \right) - \frac{3}{{{x^5}}}\geq0\\-(\cos \left( x \right) - \frac{3}{{{x^5}}})&\Leftarrow& \cos \left( x \right) - \frac{3}{{{x^5}}}<0\end{cases}$$

بنابراین خواهیم داشت:

$$\int{{\cos \left( x \right) - \frac{3}{{{x^5}}}\,dx}} = \int{{\cos \left( x \right) - 3{x^{ - 5}}\,dx}} = \sin \left( x \right) + \frac{3}{4}{x^{ - 4}} + c = \require{bbox} \bbox[2pt,border:1px solid black]{{\sin \left( x \right) + \frac{3}{{4{x^4}}} + c}}$$

$$\int{{-\cos \left( x \right) + \frac{3}{{{x^5}}}\,dx}} = \require{bbox} \bbox[2pt,border:1px solid black]{-{\sin \left( x \right) - \frac{3}{{4{x^4}}} + c}}$$

مثال هشتم انتگرال نامعین شامل قدر مطلق

می‌خواهیم انتگرال $$\int\mid{{12{x^3} - 9{x^2} + 2\,\mid dx}}$$ را حساب کنیم.

پاسخ:

در اینجا یک تابع چندجمله‌ای درون قدرمطلق قرار دارد پس باید تابع داخل قدرمطلق را یکبار برای مثبت و یکبار برای منفی باید حساب کنیم.

$$\begin{cases}3{x^4} - 3{x^3} + 2x+c&\Leftarrow& 12{x^3} - 9{x^2} + 2\geq0\\-3{x^4} + 3{x^3} - 2x+c&\Leftarrow& 12{x^3} - 9{x^2} + 2<0\end{cases}$$

مثال نهم انتگرال نامعین شامل قدر مطلق

انتگرال $$\int{\mid{\frac{{2{y^3} - 6{y^2}}}{{{y^2}}}\mid\,dy}}$$ را محاسبه کنید.

پاسخ:

در اینجا تابع داخل قدرمطلق، یک تابع کسری است. تابع داخل قدرمطلق را یکبار برای مثبت و یکبار برای منفی باید حساب کنیم.

$$\begin{cases}({\frac{{2{y^3} - 6{y^2}}}{{{y^2}}}})\Leftarrow& \frac{{2{y^3} - 6{y^2}}}{{{y^2}}}\geq0\\-({\frac{{2{y^3} - 6{y^2}}}{{{y^2}}}})\Leftarrow& \frac{{2{y^3} - 6{y^2}}}{{{y^2}}}<0\end{cases}$$

بنابراین خواهیم داشت:

$$\int{{\frac{{2{y^3} - 6{y^2}}}{{{y^2}}}\,dy}} = \int{{2y - 6\,dy}} = \left. {\left( {{y^2} - 6y} \right)}+c \right.$$

$$\int{-{\frac{{2{y^3} - 6{y^2}}}{{{y^2}}}\,dy}} = \int{{-2y + 6\,dy}} = \left. {\left( {{-y^2} + 6y} \right)}+c \right.$$

مثال دهم انتگرال نامعین شامل قدر مطلق

انتگرال $$\int\mid{{\frac{8}{{\sqrt t }} - 12\sqrt {{t^3}} \,\mid dt}}$$ را محاسبه کنید.

پاسخ:

تابع داخل قدرمطلق را یکبار برای مثبت و یکبار برای منفی باید حساب کنیم.

$$\begin{cases}({\frac{8}{{\sqrt t }} - 12\sqrt {{t^3}}})\Leftarrow& {{\frac{8}{{\sqrt t }} - 12\sqrt {{t^3}} \,}}\geq0\\-({\frac{8}{{\sqrt t }} - 12\sqrt {{t^3}}}) \Leftarrow& {{\frac{8}{{\sqrt t }} - 12\sqrt {{t^3}} \,}}<0\end{cases}$$

بنابراین خواهیم داشت:

$$\int{{\frac{8}{{\sqrt t }} - 12\sqrt {{t^3}} \,dt}} = \int{{8{t^{ - \,\,\frac{1}{2}}} - 12{t^{\frac{3}{2}}}\,dt}} = \left. {\left( {16{t^{\,\,\frac{1}{2}}} - \frac{{24}}{5}{t^{\frac{5}{2}}}} \right)}+c \right.$$

$$\int{-{\frac{8}{{\sqrt t }} + 12\sqrt {{t^3}} \,dt}} = \int{{-8{t^{ - \,\,\frac{1}{2}}} + 12{t^{\frac{3}{2}}}\,dt}} = \left. {\left( -{16{t^{\,\,\frac{1}{2}}} + \frac{{24}}{5}{t^{\frac{5}{2}}}} \right)} +c\right.$$

مثال یازدهم انتگرال نامعین شامل قدر مطلق

می‌خواهیم انتگرال $$\int\mid{{\frac{1}{{7z}} + \frac{{\sqrt[3]{{{z^2}}}}}{4} - \frac{1}{{2{z^3}}}\,\mid dz}}$$ را محاسبه کنیم.

پاسخ:

تابع داخل قدرمطلق را یکبار برای مثبت و یکبار برای منفی باید حساب کنیم.

$$\begin{cases}({\frac{1}{{7z}} + \frac{{\sqrt[3]{{{z^2}}}}}{4} - \frac{1}{{2{z^3}}}})\Leftarrow& {{\frac{1}{{7z}} + \frac{{\sqrt[3]{{{z^2}}}}}{4} - \frac{1}{{2{z^3}}}\,}}\geq0\\-({\frac{1}{{7z}} + \frac{{\sqrt[3]{{{z^2}}}}}{4} - \frac{1}{{2{z^3}}}}) \Leftarrow& {{\frac{1}{{7z}} + \frac{{\sqrt[3]{{{z^2}}}}}{4} - \frac{1}{{2{z^3}}}\,}}<0\end{cases}$$

بنابراین خواهیم داشت:

$$\int{{\frac{1}{{7z}} + \frac{{\sqrt[3]{{{z^2}}}}}{4} - \frac{1}{{2{z^3}}}\,dz}} = \int{{\frac{1}{7}\frac{1}{z} + \frac{1}{4}{z^{\frac{2}{3}}} - \frac{1}{2}{z^{ - 3}}\,dz}} = \left. {\left( {\frac{1}{7}\ln \left| z \right| + \frac{3}{{20}}{z^{\frac{5}{3}}} + \frac{1}{4}{z^{ - 2}}} \right)}+c \right.$$

$$\int{-{\frac{1}{{7z}} - \frac{{\sqrt[3]{{{z^2}}}}}{4} + \frac{1}{{2{z^3}}}\,dz}} = \int{-{\frac{1}{7}\frac{1}{z} - \frac{1}{4}{z^{\frac{2}{3}}} + \frac{1}{2}{z^{ - 3}}\,dz}} = \left. {\left( {-\frac{1}{7}\ln \left| z \right| - \frac{3}{{20}}{z^{\frac{5}{3}}} - \frac{1}{4}{z^{ - 2}}} \right)}+c \right.$$

مثال دوازدهم انتگرال نامعین شامل قدر مطلق

می‌خواهیم انتگرال $$\int\mid{{7\sin \left( t \right) - 2\cos \left( t \right) \mid dt}}$$ را محاسبه کنیم.

پاسخ:

در این مثال داخل قدرمطلق دو تابع مثلثاتی داریم. تابع داخل قدرمطلق را یکبار برای مثبت و یکبار برای منفی باید حساب کنیم.

$$\begin{cases}({7\sin \left( t \right) - 2\cos \left( t \right)})\Leftarrow& {{7\sin \left( t \right) - 2\cos \left( t \right) }}\geq0\\-({7\sin \left( t \right) - 2\cos \left( t \right)}) \Leftarrow& {{7\sin \left( t \right) - 2\cos \left( t \right) }}<00\end{cases}$$

بنابراین خواهیم داشت:

$$\int{{7\sin \left( t \right) - 2\cos \left( t \right)\,dt}} = \left. {\left( { - 7\cos \left( t \right) - 2\sin \left( t \right)} \right)+c} \right.$$

$$\int{-{7\sin \left( t \right) + 2\cos \left( t \right)\,dt}} = \left. {\left( { 7\cos \left( t \right) + 2\sin \left( t \right)} \right)+c} \right.$$

انتگرال معین شامل تابع قدر مطلق

انتگرال معین که شامل تابع قدرمطلق است را باید ابتدا ریشه‌های داخل عبارت را محاسبه کنیم سپس آن تابع را تعینن علامت می‌کنیم و بر این اساس قدرمطلق را حذف می‌کنیم و انتگرال را محاسبه و در آخر حدود جدید را اعمال می‌کنیم. برای درک بهتر این موضوع به مثال‌های زیر توجه کنید.

مثال اول انتگرال معین شامل قدر مطلق

می‌خواهیم انتگرال زیر را حساب کنیم.

$$\int_{-1}^{2} \mid 4x-3\mid dx$$

پاسخ:

ریشه‌ تابع درون قدرمطلق به صورت زیر است:

$$x=\frac{3}{4}$$

با توجه به تعریف قدرمطلق تابع را به بازه‌های زیر تفکیک می‌کنیم.

$$\begin{cases}-(4x-3) & x<\frac{3}{4}\\4x-3 & x\geq\frac{3}{4}\end{cases}$$

در نتیجه دو انتگرال خواهیم داشت.

$$\int_{-1}^{3/4} -( 4x-3) dx+\int_{3/4}^{2} ( 4x-3) dx$$

جواب انتگرال اول به صورت زیر است:

$$-(2x^2-3x)|_{-1}^{3/4}=\frac{9}{8}$$

پاسخ انتگرال دوم نیز به شکل زیر خواهد بود:

$$(2x^2-3x)|_{3/4}^{2}=\frac{41}{8}$$

بنابراین اگر آن‌ها را با هم جمع کنیم حاصل انتگرال این مثال به صورت زیر خواهد بود:

$$\int_{-1}^{2} \mid 4x-3\mid dx=\frac{50}{8}$$

مثال دوم انتگرال معین شامل قدر مطلق

می‌خواهیم انتگرال $$\int_{-4}^{0} \mid x+2\mid dx$$ را حساب کنیم.

پاسخ:

مطابق تعریف قدرمطلق تابع را به بازه‌های زیر تفکیک می‌کنیم.

$$\begin{cases}-(x+2) & x<2\\x+2 & x\geq2\end{cases}$$

در نتیجه انتگرال به صورت زیر خواهد شد:

$$\int_{-4}^{-2} (-x-2)dx+\int_{-2}^{0} (x+2)dx$$

جواب انتگرال اول به صورت زیر است:

$$(\frac{-x^2}{2}-2x)|_{-4}^{-2}=2$$

پاسخ انتگرال دوم نیز به شکل زیر خواهد بود:

$$(\frac{x^2}{2}+2x)|_{-2}^{0}=2$$

اگر آن‌ها را با هم جمع کنیم حاصل انتگرال این مثال به صورت زیر خواهد بود:

$$\int_{-4}^{0} \mid x+2\mid dx=2+2=4$$

مثال سوم انتگرال معین شامل قدر مطلق

می‌خواهیم انتگرال $$\int_{3}^{6}{{\left| {2x - 10} \right|\,dx}}$$ را حساب کنیم.

پاسخ:

با توجه به اینکه انتگرال قدرمطلق کراندار است باید ابتدا ریشه‌های تابع درون قدرمطلق را حساب کنیم و بعد تعیین علامت کنیم.

$$\begin{cases}-(2x-10) & x<5\\2x-10 & x>5\end{cases}$$

چون حدود تعیین شده داخل کران‌های انتگرال است باید انتگرال را به دو قسمت تقسیم کنیم.

$$\int_{3}^{6}{{\left| {2x - 10} \right|\,dx}} = \int_{3}^{5}{{\left| {2x - 10} \right|\,dx}} + \int_{5}^{6}{{\left| {2x - 10} \right|\,dx}}$$

در حدود انتگرال اول تابع منفی و در حدود انتگرال دوم تابع مثبت است پس از حذف قدرمطلق خواهیم داشت:

$$\int_{3}^{6}{{\left| {2x - 10} \right|\,dx}} = \int_{3}^{5}{{ - \left( {2x - 10} \right)\,dx}} + \int_{5}^{6}{{2x - 10\,dx}}$$

بنابراین می‌توانیم دو انتگرال تابع چندجمله‌ای را به راحتی محاسبه کنیم.

$$\begin{align*}\int_{3}^{6}{{\left| {2x - 10} \right|\,dx}} & = \int_{3}^{5}{{ - 2x + 10\,dx}} + \int_{5}^{6}{{2x - 10\,dx}} = \left. {\left( { - {x^2} + 10x} \right)} \right|_3^5 + \left. {\left( {{x^2} - 10x} \right)} \right|_5^6\\ & = \left[ {25 - 21} \right] + \left[ { - 24 - \left( { - 25} \right)} \right] = \require{bbox} \bbox[2pt,border:1px solid black]{5}\end{align*}$$

مثال چهارم انتگرال معین شامل قدر مطلق

می‌خواهیم انتگرال $$\int_{{ - 1}}^{0}{{\left| {4w + 3} \right|\,dw}}$$ را حساب کنیم.

پاسخ:

چون انتگرال قدرمطلق کراندار است پس باید ابتدا ریشه‌های تابع چندجمله‌ای درون قدرمطلق را حساب کنیم و بعد آن را تعیین علامت کنیم.

$$\begin{cases}-(4w + 3) & w < - \frac{3}{4}\\4w + 3 & w > - \frac{3}{4}\end{cases}$$

با توجه به اینکه حدود تعیین شده داخل کران‌های انتگرال است پس باید انتگرال را به دو قسمت تقسیم کنیم.

$$\int_{{ - 1}}^{0}{{\left| {4w + 3} \right|\,dw}} = \int_{{ - 1}}^{{ - \frac{3}{4}}}{{\left| {4w + 3} \right|\,dw}} + \int_{{ - \frac{3}{4}}}^{0}{{\left| {4w + 3} \right|\,dw}}$$

در سمت راست رابطه فوق، تابع در انتگرال اول منفی و تابع در انتگرال دوم مثبت است پس از حذف قدرمطلق خواهیم داشت:

$$\int_{{ - 1}}^{0}{{\left| {4w + 3} \right|\,dw}} = \int_{{ - 1}}^{{ - \frac{3}{4}}}{{ - \left( {4w + 3} \right)\,dw}} + \int_{{ - \frac{3}{4}}}^{0}{{4w + 3\,dw}}$$

درنتیجه می‌توانیم دو انتگرال تابع چندجمله‌ای را به راحتی محاسبه کنیم.

$$\begin{align*}\int_{{ - 1}}^{0}{{\left| {4w + 3} \right|\,dw}} & = \int_{{ - 1}}^{{ - \frac{3}{4}}}{{ - 4w - 3\,dw}} + \int_{{ - \frac{3}{4}}}^{0}{{4w + 3\,dw}} = \left. {\left( { - 2{w^2} - 3w} \right)} \right|_{ - 1}^{ - \frac{3}{4}} + \left. {\left( {2{w^2} + 3w} \right)} \right|_{ - \frac{3}{4}}^0\\ & = \left[ {\frac{9}{8} - 1} \right] + \left[ {0 - \left( { - \frac{9}{8}} \right)} \right] = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{5}{4}}}\end{align*}$$

نتیجه‌گیری

تابع قدرمطلق یگ تابع ساده و جالب در ریاضیات است که خروجی آن همیشه مثبت خواهد بود. در این مطلب از مجله فرادرس آموختید که برای محاسبه انتگرال قدرمطلق باید ابتدا تابع درون قدرمطلق را یکبار به ازای مقادیر مثبت و بار دیگر به ازای مقادیر منفی حساب کنید و بعد انتگرال را براین اساس تفکیک کنید تا بتوانید علامت قدرمطق را حذف کنید، سپس انتگرال‌های باقی‌مانده را با روش مناسب خود حل کنید.