ضرب متقاطع یا طرفین و وسطین – به زبان ساده
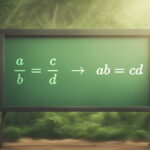
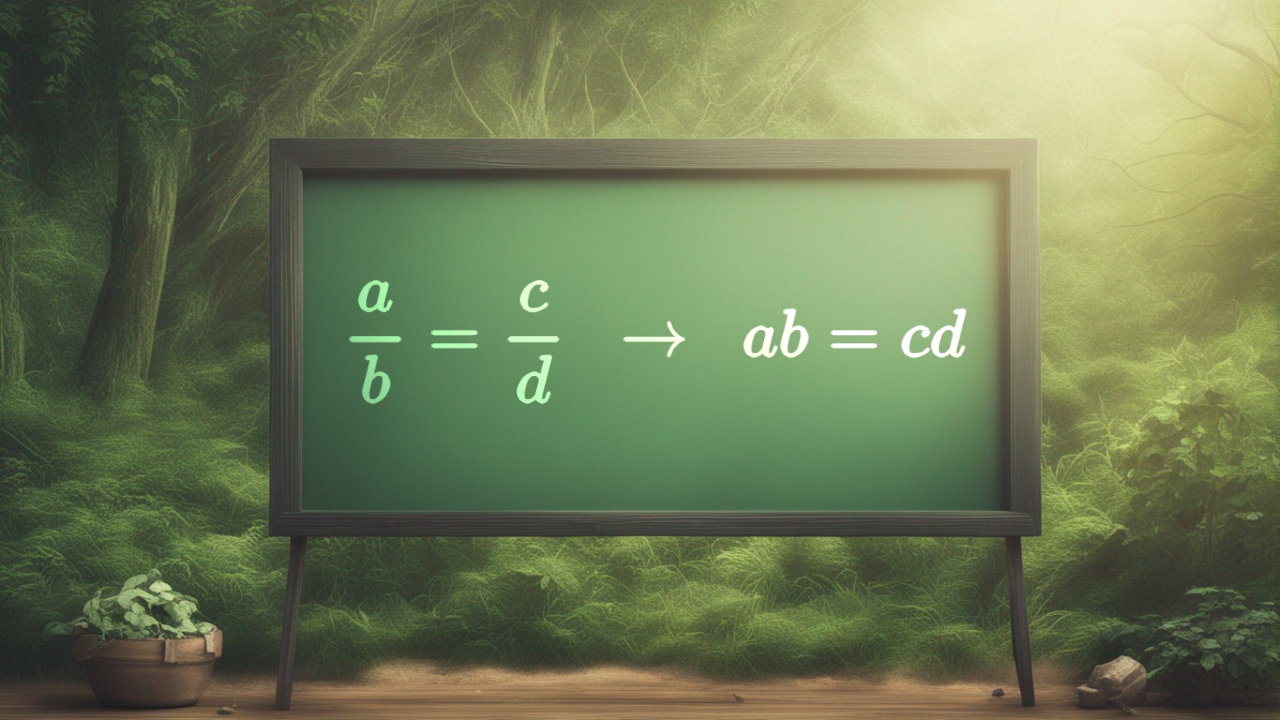
ضرب متقاطع یا طرفین و وسطین اصطلاحی در ریاضیات است که یک رابطه را میان صورت و مخرج دو کسر مساوی برقرار میکند و کاربرد بسیار زیادی در حل معادلات کسری و نسبی دارد. همچنین بسیاری از مسائل پیچیده به کمک این رابطه، ساده و قابل محاسبه خواهند شد.
فرض کنید که دو کسر مساوی به شکل زیر داشته باشیم.
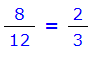
رابطه ضرب متقاطع یا طرفین و وسطین، برای این دو کسر به شکل زیر نمایش داده میشود.
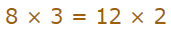
این رابطه، نشان میدهد که اگر دو کسر مساوی داشته باشیم، حاصل ضرب صورت کسر اول در مخرج کسر دوم با حاصل ضرب صورت کسر دوم در مخرج کسر اول، برابر خواهد بود.

اثبات رابطه ضرب متقاطع یا طرفین و وسطین
یکی از قوانین بسیار مهم در کسرها این است که اگر صورت و مخرج کسری را در یک عدد ضرب کنیم، حاصل کسر تغییری نخواهد کرد.
بنابراین دو کسر مساوی مانند رابطه ۱ را در نظر بگیرید. صورت و مخرج کسر سمت چپ را در مخرج کسر سمت راست (مخرج کسر سمت راست عدد ۳ است) ضرب کنید. عبارت حاصل به شکل زیر در میآید.
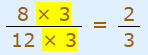
در ادامه، صورت و مخرج کسر سمت راست رابطه بالا را در مخرج کسر سمت چپ رابطه ۱ (مخرج کسر سمت چپ رابطه ۱ برابر با 12 است) ضرب کنید. با استفاده از این کار، کسر فوق به شکل زیر در میآید.
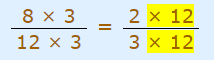
همانطور که مشاهده میکنید مخرج دو کسر بالا با یکدیگر برابر هستند. بنابراین صورت آن دو نیز با یکدیگر برابر خواهند بود. تساوی صورتها، همان رابطه 2 یعنی رابطه ضرب متقاطع یا طرفین و وسطین را نشان میدهد. این رابطه به شکل زیر نوشته میشود.
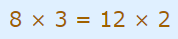
توجه شود که در مسائل مختلف، روندی که در بالا توضیح داده شد (روابط 3 تا ۵) را طی نمیکنیم و تنها رابطه نهایی یعنی همان رابطه ۲ را مینویسیم.
ضرب متقاطع یا طرفین و وسطین در حالت کلی
برای بیان رابطه ضرب متقاطع یا طرفین و وسطین در حالت کلی، چهار متغیر c ،b ،a و d را در نظر بگیرید که با استفاده از دو کسر زیر با یکدیگر رابطه داشته باشند.
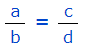
عبارت ضرب متقاطع یا طرفین و وسطین، برای کسر نشان داده شده، به شکل زیر بیان میشود.
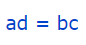
رابطه فوق را به شکل زیر هم میتوان نمایش داد.
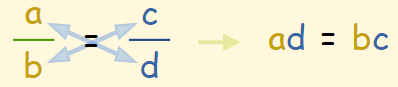
توجه کنید که دو کسر فوق، زمانی که b و d برابر با صفر باشند، تعریف نشده خواهند بود.
مثال
عبارت x را در رابطه کسری زیر محاسبه کنید.
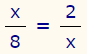
رابطه طرفین و وسطین را میتوان برای تساوی فوق بیان کرد. بنابراین حاصل ضرب صورت کسر سمت راست (2) در مخرج کسر سمت چپ (8) را با حاصل ضرب صورت کسر سمت چپ (x) در مخرج کسر سمت راست (x) برابر قرار میدهیم. فرم نهایی این عبارت به شکل زیر نشان داده میشود.

x از این رابطه به شکل زیر قابل محاسبه است.
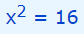

این دو عدد را در کسر ابتدای مثال قرار دهید و درستی جوابها را مورد بررسی قرار دهید.
مقایسه دو کسر با استفاده از ضرب متقاطع یا طرفین و وسطین
برای درک صحیح شیوه مقایسه دو کسر با استفاده از ضرب متقاطع، دو کسر به شکل زیر را در نظر بگیرید.

برای این که کسر بزرگتر را تعیین کنیم، طرفین و وسطین را برای دو کسر بالا به شکل زیر بیان میکنیم.


بنابراین از آنجایی که عدد ۱۶ بزرگتر از عدد ۱۵ است، میتوان نتیجه گرفت که کسر بزرگتر از کسر است.
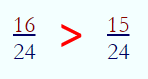
کاربرد طرفین وسطین در حل مسائل نسبی
در بخش قبل به بیان کاربرد رابطه ضرب متقاطع یا طرفین و وسطین در حل معادلات ریاضی و مقایسه دو کسر پرداخته شد. این قسمت به بررسی کاربرد این مفهوم در حل مسائل نسبی میپردازد. برای نشان دادن این مفهوم، مثال زیر را در نظر بگیرید.
مثال
یک نقشه با مقیاسی معلوم را در نظر بگیرید. سانتیمتر در این نقشه، 60 کیلومتر در واقعیت را نشان میدهد. محاسبه کنید که ۲ سانتیمتر در این نقشه چند کیلومتر در واقعیت را نشان میدهد.
برای به دست آوردن پاسخ این مثال، جدولی را به شکل زیر تشکیل میدهیم.
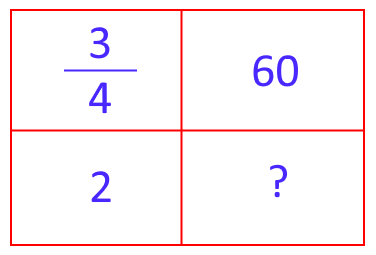
این جدول نشان میدهد که سانتیمتر در نقشه، نشان دهنده 60 کیلومتر در دنیای واقعی است. حال 2 سانتیمتر در نقشه، چند کیلومتر در دنیای واقعی را نشان میدهد.
بنابراین برای محاسبه علامت سوال، طرفین و وسطین میکنیم. مقدار علامت سوال را x در نظر میگیریم. بنابراین داریم:
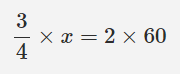
x از رابطه فوق برابر با 160 محاسبه میشود. بنابراین ۲ سانتیمتر در نقشه، 160 گیلومتر در دنیای واقعی را نشان میدهد.
همانطور که نشان داده شد، رابطه ضرب متقاطع که به آن طرفین و وسطین نیز گفته میشود، کاربرد بسیار زیادی در مسائل ریاضی دارد. این رابطه را میتوان در مسائل نسبی شیمی و فیزیک نیز مورد استفاده قرار داد.
این مطلب، ابتدا مفهوم و رابطه کلی ضرب متقاطع را مورد بررسی قرار داد. سپس نحوه محاسبه و اثبات عبارت ضرب متقاطع بیان شد و با استفاده از یک مثال کاربرد این عبارت نیز نشان داده شد. در ادامه، کاربرد رابطه ضرب متقاطع برای مقایسه کسرها و حل مسائل نسبی با استفاده از چند مثال مورد بررسی قرار گرفت.












سلام و درود،چه زمانی تو انجام طرفین وسطین محدودیت هست؟
سلام و وقت بخیر؛
به طور کلی، محدودیت خاصی برای طرفین وسطین وجود ندارد؛ مگر اینکه بخواهید در یک نامساوی از این روش استفاده کنید. هنگام طرفین وسطین در نامساویها (بزرگتر، بزرگتر مساوی، کوچکتر و کوچکتر مساوی)، امکان تغییر علامت وجود دارد. مثلا اگر طرفین وسطین را بدون توجه به علامت منفی بر روی نامساوی –21<21 اجرا کنید، به جواب اشتباه 2<–2 میرسید. در مسائل دارای متغیر و نامساوی، توجه به این نکته بسیار ضروری است. در مسائل دارای مساوی، محدودیتی در اجرای طرفین وسطین وجود ندارد.
از همراهی شما با مجله فرادرس سپاسگزاریم.
چرا در مثال آخر توضیح نداد که چجوری به عدد 160 رسیده، من مثال آخر رو درک نکردم.
با سلام و وقت بخیر؛
برای درک بهتر، روند حل به متن اضافه شد.
از همراهی شما با مجله فرادرس سپاسگزاریم
ممنون میشگم
بی نهایت عالی ،سپاس فراوان
ای قربان شما کلی چیز میز یاد گرفتم نوکرتم غلامتم
من از بهنام محمدیان ممنونم واقعا بهشون خسته نباشی میگم و متشکر از این مطالب اموزشی که در اختیار ما ها قرار میدند و همچنین از سایت فرادرس که چنین محیطی در بستر سایت اموزشی در اختیار همه دانشجویان و دانش اموزان قرار داده .
ممنون?
دمت گرم داداش
ممنون، خیلی عالی توضیح داده شده
بسیار ممنونم از مطالب کامل و مفیدتون که قرار میدین