فیلترهای اکتیو مرتبه اول — به زبان ساده (+ دانلود فیلم آموزش رایگان)
در آموزشهای پیشین مجله فرادرس، با فیلترهای الکترونیکی و برخی فیلترهای پسیو آشنا شدیم. فیلترهای پسیو، سه محدودیت اصلی دارند؛ اول اینکه بهره بالاتر از ۱ ندارند، زیرا اجزای پسیو قادر به افزایش انرژی شبکه نیستند. مسئله دوم این است که فیلترهای پسیو ممکن است به سلفهای بزرگ و سنگین نیاز داشته باشند. عیب سوم فیلترهای پسیو، این است که در فرکانسهای کمتر از محدوده فرکانس رادیویی ($$30 Hz<f<3000 Hz$$)، عملکرد ضعیفی دارند. در این آموزش، نگاهی کلی بر فیلترهای اکتیو خواهیم داشت.
فیلترهای اکتیو، از ترکیب مقاومت، خازن و تقویتکننده عملیاتی تشکیل شدهاند. این فیلترها، مزیتهایی نسبت به فیلترهای RLC پسیو دارند. اول اینکه، فیلترهای اکتیو، کوچکتر و ارزانتر هستند، زیرا به سلف نیاز ندارند. این موضوع، تعبیه فیلترهای اکتیو را در مدارهای مجتمع تسهیل میکند. مزیت دیگر فیلترهای اکتیو این است که میتوان آنها را با تقویتکنندههای بافر (ولتاژ فالوئرها) برای ایزوله کردن هر طبقه از اثرات امپدانس منبع و بار، فیلتر کرد. با استفاده از این ایزولاسیون میتوان طبقهها را مستقل از یکدیگر طراحی و آنها را برای دست یافتن به تابع تبدیل مورد نظر بهصورت متوالی به هم وصل کرد. البته، فیلترهای اکتیو نسبت به فیلترهای پسیو، قابلیت اطمینان و پایداری کمتری دارند. حداکثر فرکانس عملی اغلب فیلترهای اکتیو، حدود $$100 Hz$$ است و اکثر آنها در فرکانسی کمتر از آن کار میکنند. فیلترها را اغلب براساس مرتبه (یا تعداد قطبهای) آنها یا نوع خاص طراحی دستهبندی میکنند.
فیلتر پایینگذر مرتبه اول
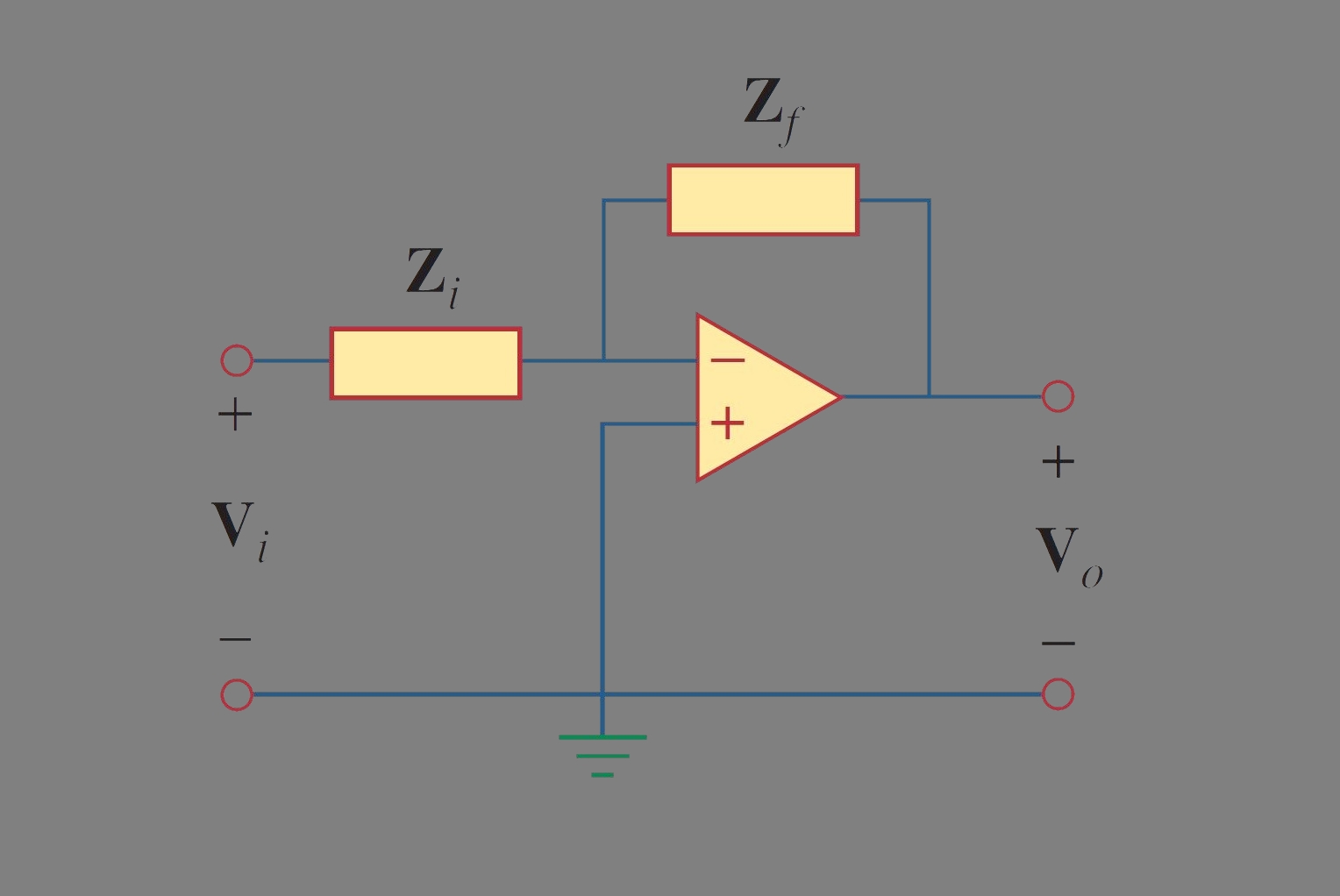
یک فیلتر مرتبه اول نوعی در شکل ۱ نشان داده شده است.
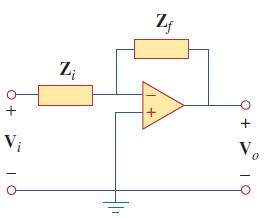
مولفههای $$Z_i$$ و $$Z_f$$ تعیین میکنند که یک فیلتر پایین گذر است یا بالا گذر؛ اما یکی از مولفهها حتماً باید راکتیو باشد. شکل ۲، یک فیلتر پایین گذر اکتیو را نشان میدهد.
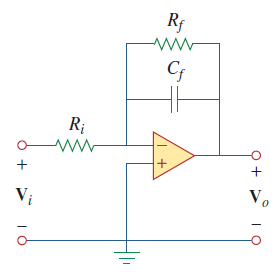
تابع تبدیل این فیلتر، برابر است با:
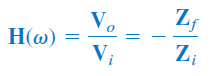
که در آن، $$Z_i=R_i$$ و
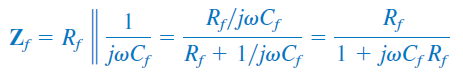
بنابراین،:
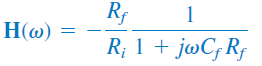
معادله اخیر، شبیه تابع تبدیل فیلتر پایین گذر پسیو است، با این تفاوت که یک بهره فرکانس پایین ($$\omega \to 0$$) یا dc بهاندازه $$-R_f/R_i$$ دارد. همچنین، فرکانس گوشه برابر است با:
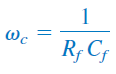
که به $$R_i$$ بستگی ندارد.
فیلتر بالاگذر مرتبه اول
شکل 3، یک فیلتر بالاگذر را نشان میدهد.
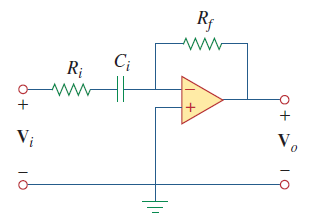
همانطور که قبلاً گفتیم:
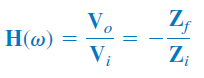
که در آن، $$Z_i=R_i+1/i \omega C_i$$ و $$Z_f=R_f$$. بنابراین:
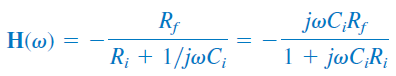
تابع تبدیل فوق، شبیه تابع تبدیل فیلتر پسیو است، با این تفاوت که در فرکانسهای بسیار بالا ($$\omega \to \infty$$) بهره آن به $$-R_f/R_i$$ میل میکند. فرکانس گوشه این فیلتر، از رابطه زیر بهدست میآید:
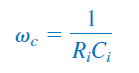
فیلتر میان گذر
مدار شکلهای ۲ و ۳ را میتوان با یکدیگر ترکیب کرد و یک فیلتر میان گذر را با بهره $$K$$ برای محدوده فرکانسهای مورد نیاز ساخت. همانگونه که در شکل ۴ (الف) نشان داده شده است، با اتصال متوالی یک فیلتر پایین گذر با بهره واحد، یک فیلتر بالاگذر با بهره واحد و یک معکوس کننده (اینورتر) با بهره $$-R_f/R_i$$ میتوان این کار را انجام داد.
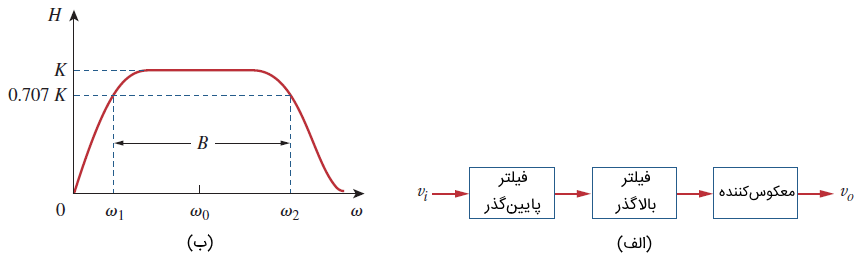
تحلیل فیلتر میان گذر نسبتاً ساده است. تابع تبدیل این فیلتر، با ضرب توابع تبدیل فیلتر پایین گذر و بالاگذر در بهره معکوس کننده بهدست میآید. بنابراین، داریم:
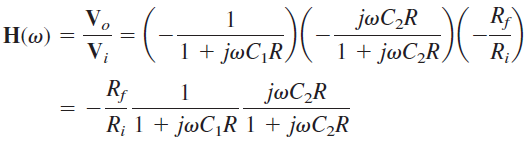
بخش پایین گذر، فرکانس گوشه بالا را تعیین میکند:
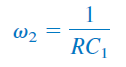
در حالی که بخش فرکانس بالا، فرکانس گوشه پایین را بهصورت زیر نتیجه میدهد:
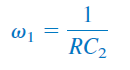
با مقادیر $$\omega _1$$ و $$\omega _2$$ میتوان فرکانس میانی، پهنای باند و ضریب کیفیت را بهصورت زیر نوشت:
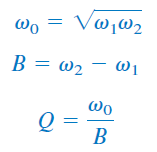
برای یافتن بهره میان گذر $$K$$، تابع تبدیل این فیلتر را به شکل استاندارد زیر مینویسیم:
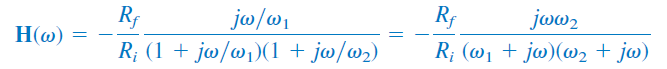
در فرکانس میانی $$\omega _0 = \sqrt{ \omega _1 \omega _2}$$، اندازه تابع تبدیل برابر است با:
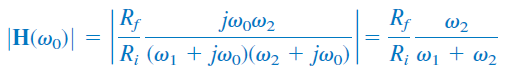
در نتیجه، بهره میان گذر را میتوان بهصورت زیر بهدست آورد:
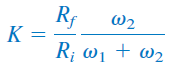
فیلتر میان ناگذر (یا شکافی)
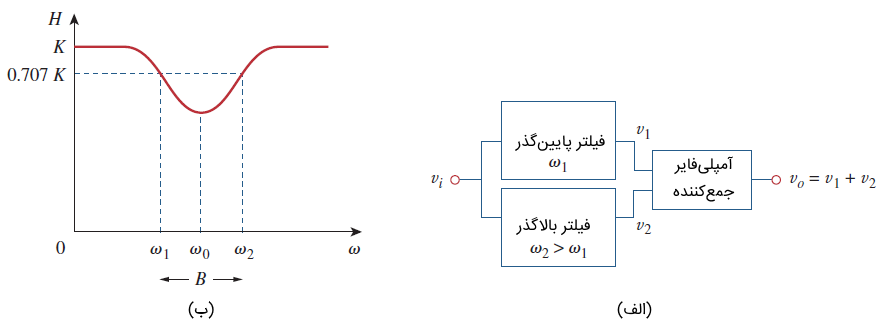
یک فیلتر میان ناگذر را میتوان با ترکیب موازی یک فیلتر پایین گذر و یک فیلتر بالاگذر به همراه آمپلی فایر جمع کننده مطابق شکل ۵ (الف) ساخت. مدار فیلتر بهگونهای طراحی میشود که فرکانس قطع پایین $$\omega _1$$، با فیلتر پایین گذر تعیین میشود، در حالی که فیلتر بالاگذر، فرکانس قطع بالای $$\omega _2$$ را مشخص میکند. فاصله بین $$\omega _1$$ و $$\omega _2$$، پهنای باند فیلتر است.
همانگونه که در شکل ۵ (ب) نشان داده شده است، فیلتر، فرکانسهای کوچکتر از $$\omega _1$$ و بزرگتر از $$\omega _2$$ را عبور میدهد. نمودار بلوکی شکل ۵ (الف)، دقیقاً در شکل ۶ پیادهسازی شده است.
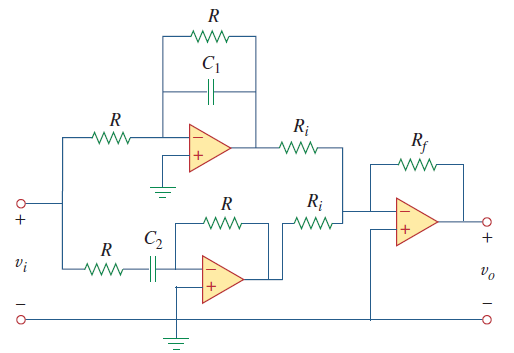
تابع تبدیل فیلتر میان ناگذر، بهصورت زیر است:
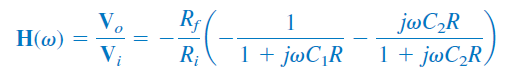
مقادیر $$\omega _1$$، $$\omega _2$$، فرکانس میانی، پهنای باند و ضریب کیفیت فیلتر میان ناگذر، براساس روابطی که در بالا گفته شد، بهدست میآیند.
برای تعیین بهره میان گذر $$K$$، میتوان تابع تبدیل فیلتر میان ناگذر فوق را برحسب فرکانسهای گوشه بالا و پایین بهصورت زیر نوشت:
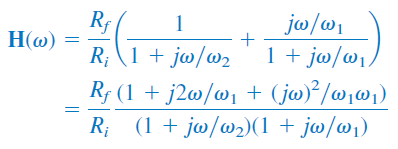
در دو مورد $$\omega \to 0$$ و $$\omega \to \infty$$، بهره برابر است با:
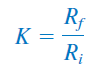
همچنین، میتوانیم با یافتن اندازه تابع تبدیل، بهره را در فرکانس میانی $$\omega _0 = \sqrt{\omega _1 \omega _2}$$ بنویسیم:
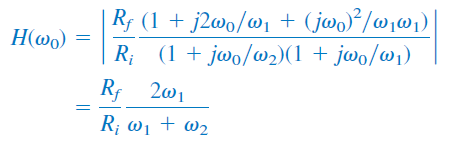
مثال
یک فیلتر اکتیو پایین گذر طراحی کنید که بهره dc و فرکانس گوشه آن، بهترتیب 4 و 500 هرتز باشد.
حل: همانطور که گفتیم، فرکانس گوشه یا فرکانس قطع را میتوان بهصورت زیر محاسبه کرد:
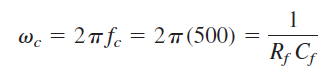
بهره dc نیز برابر است با
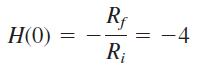
اکنون دو معادله و سه پارامتر مجهول داریم. اگر $$C_f=0.2 \mu F$$ را انتخاب کنبم، سایر پارامترها بهصورت زیر بهدست میآیند:
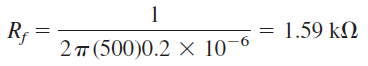
و
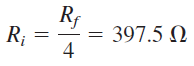
با توجه به محاسبات، مقدار مقاومتها را $$R_f=1.6 k\Omega$$ و $$R_i=400 \Omega$$ در نظر میگیریم.
اگر مطالب بیان شده برای شما مفید بوده و علاقهمند به یادگیری مباحث مرتبط با آن هستید، پیشنهاد میکنیم به آموزشهای زیر مراجعه کنید:
^^










