یادگیری ماشین به زبان قضیه بیز، بی نظمی شانون و فلسفه

شاید به نظر برسد که ایده‌های مربوط به «یادگیری ماشین» (Machine Learning) بسیار جدید باشند ولی با مطالعه در زمینه‌های آمار، فلسفه و نظریه اطلاع متوجه خواهیم شد که آنچه امروزه به نام یادگیری ماشین می‌شناسیم، به کارگیری ایده‌هایی است که در این سه زمینه از قبل وجود داشته است.

در این نوشتار سعی می‌کنیم، این سه زمینه یعنی آمار، نظریه اطلاع (بی‌نظمی) و فلسفه را در کنار هم قرار دهیم تا به کابردهای آن‌ها در تعاریف و اصول اولیه یادگیری ماشین برسیم. بنابراین بهتر است قبل از مطالعه این نوشتار، مطالب قضیه بیز در احتمال شرطی و کاربردهای آن و احتمال پسین (Posterior Probability) و احتمال پیشین (Prior Probability) — به زبان ساده را مطالعه کرده باشید. همچنین به منظور با مفاهیم یادگیری ماشین مطلب مقدمه‌ای بر یادگیری ماشین را مطالعه کرده باشید. همچنین خواندن مطلب تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده نیز خالی از لطف نیست.

قضیه بیز، بی نظمی شانون و فلسفه

شاید برایتان عجیب باشد که برای موضوعی مثل یادگیری ماشین که بسیار به روز و جدید به نظر می‌رسد، ریشه‌هایی بس قدیمی در علوم دیگر وجود داشته باشد. ولی باید گفت که در حقیقت چیزی که امروزه به نام یادگیری ماشین می‌شناسیم وام‌دار علوم آمار، نظریه اطلاع و فلسفه است. بنابراین بهتر است ابتدا به معرفی مباحثی بپردازیم که در این سه زمینه به کار گرفته شده‌اند تا با ارتباط آن‌ها، مفاهیم یادگیری ماشین را بهتر درک کنیم.

فیلم آموزش مقدماتی استنباط و آمار بیزی در فرادرس

کلیک کنید

قضیه بیز (Bayesian Theorem)

در نیمه دوم قرن ۱۸، هنوز شاخه‌ای از ریاضیات به نام آمار و احتمال بوجود نیامده بود. در نتیجه بیشتر قضیه‌ها و تئوری‌‌های احتمال توسط ریاضی‌دانان شناخته و اثبات می‌شد. به این ترتیب اصول و قضیه‌های احتمال را «الگوهای شانس«» (Doctrine of Chances) می‌نامیدند زیرا در کتابی که توسط دمویر (Abraham de Moievre) نوشته شده بود، او از این اصطلاح استفاده کرده بود. در مقاله‌ای با نام «روش‌های محاسبات در الگوهای شانسی» (An Essay towards solving a Problem in the Doctrine of Chances) که توسط بیز در سال 1763 نوشت و توسط دوستش ریچار پرایس (Richard Price) منتشر شد نیز به بررسی شیوه محاسبه احتمال برای پدیده‌های شانسی و تصادفی پرداخته شده است.

او در این مقاله که به نظر ساده می‌آمد، احتمال توام، احتمال شرطی و احتمال حاشیه‌ای را مطرح کرد و به کمک آن‌ها عکس قضیه احتمال شرطی را ارائه داد.

از آن به بعد بین دو گروه از پیروان مکتب «احتمال برمبنای فراوانی» (Probability Bases on Frequency) و  «احتمال برمبنای بیز» (Bayesian Probability) اختلاف نظر و درگیری‌های زیادی بوجود آمده است. ولی بهتر است به دور از این اختلاف نظرها به منطق و دستآورد قضیه بیز بپردازیم.

اگر A و B دو پیشامد از فضای نمونه باشند، آنگاه می‌توان احتمال A به شرط B را برحسب احتمال B نوشت. این رابطه در زیر دیده می‌شود.

$$\large P(A|B)=\dfrac{P(B|A)P(A)}{P(B)}$$

به طرف راست این تساوی، احتمال پسین می‌گویند. همچنین قسمت اول صورت کسر نیز، تابع درستنمایی و قسمت آخر هم احتمال پیشین نامیده می‌شود.

این رابطه می‌تواند تصورات و نظر ما را در مورد احتمال رخداد (احتمال پیشین) یک پیشامد با استفاده از شواهدی که در دست داریم (تابع درستنمایی) بهبود بخشیده و مقدار احتمال جدیدی به نام احتمال پسین را ارائه دهد.

البته ممکن است شواهدی که توسط داده‌ها تهیه شده در جهت تایید یا خلاف احتمال پیشین باشند. ولی به هر حال انتظار است که اطلاعات اضافه حاصل شده از مشاهدات در دقت محاسبه احتمال آن پدیده شانسی موثر باشند. به این ترتیب به کمک این رابطه می‌توانید فرضیاتی که در رابطه به احتمال رخداد یک پدیده دارید را بهبود دهید.

در مباحث مربوط به آمار و احتمال، فرضیات همان اعتقادات ما در مورد طبیعت پدیده‌های شانسی هستند که ممکن است هرگز نیز موفق به دیدن آن‌ها نشویم. ولی می‌توانیم به کمک متغیرهای تصادفی (که می‌توانیم مقدار آن‌ها را البته با کمی خطا، اندازه‌گیری کنیم) حدسیاتی نسبتا دقیق در مورد پارامترهای (طبیعت) اتفاقات تصادفی (پدیده‌های شانسی) داشته باشیم.

معمولا در آمار برای متغیرهای تصادفی یک توزیع احتمالی در نظر گرفته می‌شود. ولی در مباحث یادگیری ماشین این توزیع احتمال را می‌توان مجموعه‌ای از قوانین (منطقی یا پردازش‌ها) در نظر گرفت که توسط مثال یا «داده‌های آموزش» (Training Data) قابل ایجاد و حتی به‌روزرسانی هستند تا نقاط مخفی و تاریک پدیده‌های شانسی را نمایان کنند.

با این شرح سعی می‌کنیم در ادامه قضیه بیز را به زبان یادگیری ماشین و «علم داده» (Data Science)، نمایش و توضیح دهیم. به این ترتیب در اینجا، مجموعه داده را با D و فرضیه را با h نمادی گذاری می‌کنیم. پس با این کار سعی داریم که رابطه شناخته شده بیز را برای تشخیص اینکه چه فرضیه (قانونی) در بین داده‌ها وجود دارد به کار بگیریم.

براساس این نمادها، دوباره رابطه بیز را می‌نویسیم:

$$\large P(h|D)=\dfrac{P(D|h)P(h)}{P(D)}$$

به این ترتیب به نظر می‌رسد که فضای فرضیات، می‌تواند بی‌نهایت بزرگ یا تعداد فرضیات خیلی زیاد باشد. مزیت استفاده از «استنباط بیزی» (Bayesian Inference) در این است فرضیاتی را انتخاب می‌کند که بیشترین شباهت را با داده‌های مشاهده شده دارند. زیرا در دنیای احتمالات، چیزی که واقعا اتفاق افتاده و قابل اندازه‌گیری است همان مقدارهای متغیرهای تصادفی یعنی مشاهدات هستند.

با این ترتیب، قضیه بیز از فرضیه (یا باورهایی در مورد پارامترهای مدل یادگیری ماشین) حمایت می‌کند که بتواند داده‌های شبیه مشاهدات موجود تولید کند. به بیان دیگر در استنباط بیزی فرضیه‌ای که براساس مشاهدات مقدار $$P(h|D)$$ بزرگتری را داشته باشد نسبت به بقیه فرضیه‌ها قابل قبول‌تر است. این روش را با نام «حداکثر احتمال پسین» (Maximum a Posterior) می‌شناسیم. گاهی به این روش MAP (که سرکلمه‌های عبارت انگلیسی است) نیز می‌گویند.

حالا از ترفندهای ریاضی زیر کمک می‌گیریم تا به رابطه ساده‌تری دست پیدا کنیم:

• برای بیشنه‌سازی تابع احتمال پسین در بین فرضیه‌های مختلف، فقط کافی است صورت رابطه قبل را بیشینه کرد. پس می‌توان از مخرج که برحسب h نیست صرف‌نظر کرد.
• از آنجایی که بیشینه‌سازی برای بک تابع به مانند بیشینه‌سازی لگاریتم آن است (زیرا لگاریتم یک تابع اکیدا یکنوا و یک به یک است)، از بیشینه‌سازی لگاریتم تابع احتمال پسین استفاده می‌کنیم.
• براساس خصوصیات تابع لگاریتم می‌دانیم که لگاریتم حاصل ضرب مقدارها برابر با جمع لگاریتم‌ آن‌ها است.
• بیشینه‌سازی یک مقدار به مانند کمینه‌سازی قرینه آن است. (به جای پیدا کردن نقطه ماکزیمم یک تابع می‌توان کمترین مقدار را برای قرینه تابع جستجو کرد)
• به منظور نشان دادن نقطه‌ای که باعث بیشینه شدن می‌شود از عبارت arg max استفاده می‌کنیم ،که منظور آرگومان (متغیر) از تابع است که باعث بیشینه شدن تابع می‌شود.

حال عبارت مربوط به صورت کسر که در قضیه بیز دیدیم را به صورت بیشینه می‌نوسیم:

$$\large h_{MAP}=\arg \max P(D|h)P(h)= \arg \max \log_2(P(D|h)P(h))=$$
$$\large \arg \max [log_2P(D|h)+\log_2P(h)]=\arg \min [-\log_2P(D|h)-\log_2P(h)]$$

به نظر می‌رسد عبارت‌هایی که در سطر آخر دیده می‌شوند در زمینه دیگری از علم معنی و مفهومی دارند. پس بهتر است برای ارتباط بیشتر این رابطه با یادگیری ماشین در اینجا وارد بخش جدیدی به نام «نظریه اطلاع« (Information Theory) شویم.

شانون و نظریه اطلاع

هر چند تا به امروز چندین کتاب و مقاله در مورد نظریه اطلاع نوشته شده است ولی هنوز جا برای پرداختن به این نظریه که توسط «کلود شانون» (Cloude Shannon) در ابتدای قرن ۲۰ معرفی شد، وجود دارد. او در سن ۲۲ سالگی نشان داد که چگونه می‌توان از جبر گزاره‌های منطقی که در اولایل قرن ۱۹ توسط «جورج بول» (George Boole) ابداع شد به ساخت مدارهای الکترونیکی مانند رله (relay) و سوئیچ (switch) رسید. این اجزا از قطعات پایه و اصلی برای یارانه‌های رقمی (Digital Computers) محسوب می شوند.

فیلم آموزش مدل های نمایی صف با یک سرویس دهنده (M/M/1) (رایگان) در فرادرس

کلیک کنید

نمایش منطق دو دویی توسط ۰ و ۱ یا «درست» (True) و «غلط» (False) در الکترونیک توسط باز یا بسته بودن یک کلید می‌تواند شبیه‌سازی شود. به این ترتیب شانون به کمک نظریه خود توانست منطق دو دویی را تبدیل به تجزیه و تحلیل‌های ماشینی بکند.

البته این کار بزرگترین دستآورد او محسوب نمی‌شود. در سال ۱۹۴۱، شانون به آزمایشگاه‌های بل (Bell Labs) رفت و روی پروژه‌های جنگی مانند رمزنگاری و نظریه‌هایی که برمبنای اطلاعات و انتقال آن‌ها بود، فعالیت کرد. در سال ۱۹۴۸ او در طی مقاله‌ای نتایج حاصل از تحقیقاتش در آزمایشگاه‌های بل را منتشر کرد.

شانون میزان اطلاعاتی که توسط یک منبع (برای مثال یک پیام) وجود دارد را براساس یک رابطه ریاضی به مانند رابطه‌ای که بی‌نظمی در ترمودینامیک دارد مطرح کرد.

به عنوان یک تعریف ساده، بی‌نظمی اطلاعات شانون، عددی برمبنای ۲ است که می‌تواند یک پیام را به رمز در بیاورد. در نتیجه برای به رمز درآوردن یک پیام یا یک پیشامد با احتمال رخداد p، احتیاج به $$-log_2(p)$$ بیت داریم. این دقیقا همان نکته‌ای است که که در رابطه با بیشینه‌سازی احتمال پسین که توسط رابطه بیز معرفی کردیم، دیده می‌شود.

با استفاده از دیدی که شانون به ما در مورد پیشامدها و بی‌نظمی می‌دهد می‌توان رابطه بیز را به جای احتمال، برحسب مفهوم طول $$(Length)$$ و کمینه‌سازی آن نوشت. با این کار رابطه قبلی، به صورت زیر درخواهد آمد:

$$\large h_{MAP}=\arg \min (Length(D|h)+Length (h))$$

ولی منظور از نماد Length یا طول در اینجا چیست؟ در این قسمت برای آشنایی با این مفهوم بهتر است که وارد یک بحث فلسفی شویم.

طول و تیغ اکام (Occam's Razor)

ویلیام اوکام (William of Ockham) یک نظریه پرداز و فیلسوف انگلیسی-فرانسوی بود که در سال‌های 1287-1347 میلادی می‌زیست. از او، کلمات قصار زیبایی در زمینه‌های فلسفه و علم به یادگار مانده که یکی از آن‌ها به عنوان «تیغ اکام» (Occam's Razor) معروف است. منظور از تیغ در اینجا ابزاری است که اضافات و قسمت‌های غیر ضروری را از بدنه اصلی جدا می‌کند.

ترجمه عبارت اصلی که به او نسبت داده می‌شود به این شکل است:

«توصیف با کمترین فرضیات به احتمال قوی درست‌ترین است.»

به بیان دیگر

«تا زمانی که احتیاجی به اضافه کردن نیست، چیزی نیافزایید.»

البته اندیشمندان دیگر نیز این موضوع را به بیان خودشان توضیح داده‌اند. برای مثال «اسحاق نیوتن» (Sir Issac Newton) ریاضی و فیزیکدان شهیر، می‌گوید:

«ما باید برای توصیف پدیده‌های طبیعی از رابطه‌های صحیح و کافی (حداقل ممکن) استفاده کنیم.»

یا مثلا «برتراند راسل» (Bertrand Russell) ریاضیدان و فیلسوف بزرگ در همین رابطه می‌گوید:

«تا جایی که امکان دارد، هویت‌های شناخته شده را برای استنباط در مورد چیزهایی که شناخته شده نیستند، به کار ببرید.»

به نظر می‌رسد که همه این جملات ما را به استفاده از حداقل فرضیات در استنباط سوق می‌دهند. در آمار و آزمون‌های فرض‌ آماری، می‌توان این عبارت را دستمایه انتخاب شرط‌ها و فرضیه‌ها قرار داد. به این معنی که باید برای توصیف رفتار داده‌ها، از کمترین و ساده‌ترین فرض‌ها استفاده کرد. بهتر است دوباره به عبارت طول (Length) فرضیات برگردیم. به نظر شما در تصویر زیر طول کدام درخت تصمیم کمتر است؟ درخت A یا B؟ به نظر می‌رسد که حتی بدون آشنایی با درخت تصمیم، همگی رای به کوتاه‌تر بودن گزینه A خواهیم داد.

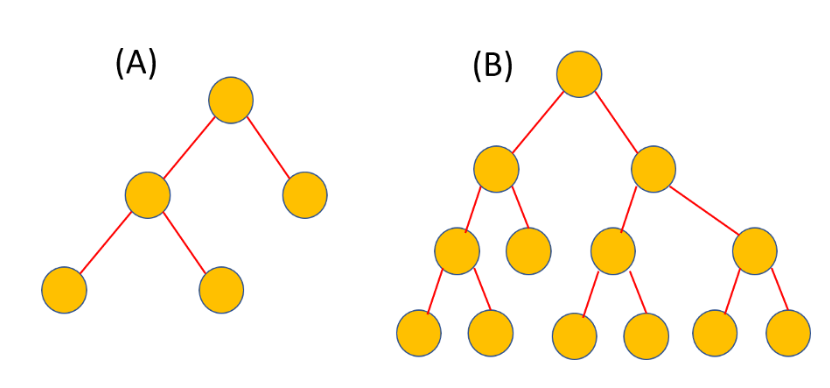
اگر در تصمیمات A و B تعداد شاخه‌ها و یا دایره‌ها را پارامترهای مربوط به هر تصمیم در نظر بگیریم، درخت تصمیم A دارای پارامترهای کمتری است در نتیجه پیچیدگی کمتری دارد. همانطور که «اوکام» در نظر داشت. بنابراین برای مثال در مسائل مربوط به دسته‌بندی به دنبال مدلی هستیم که با کمترین پارامترها یا پیچیدگی، میزان انطباق بیشتری را با دسته‌های واقعی ایجاد کند.

منظور از $$Length(D|h)$$ چیست؟

از این عبارت به عنوان طول داده‌ها به شرط فرض h استفاده می‌کنیم. ولی طول داده‌ها به چه معنا است.

فیلم آموزش یادگیری ماشین با پایتون – ماشین لرنینگ با Python در فرادرس

کلیک کنید

به طور شهودی می‌توان رابطه بین داده‌ها و فرضیات را میزان توصیف‌پذیری داده‌ها توسط فرضیات بیان کرد. به شکل دیگر می‌توان گفت که اگر مدل (و فرضیات مربوط به آن) وجود داشته باشد، چقدر در تولید داده‌ها می‌تواند موفق باشد. اگر مدل موفق شود که داده‌ها را بدون خطا باز-تولید کند، دیگر احتیاجی به ثبت و نگهداری داده‌ها نیست.

قوانین حرکت نیوتن را به یاد آورید. وقتی که اولین بار این قوانین در کتاب «اصول ریاضی برای فلسفه طبیعت» (Mathematical Principles of Natural Philosophy) توسط نیوتن در سال 1687 منتشر شد، هیچ اثباتی برای آن‌ها ارایه نشد زیرا آن‌ها قضیه یا فرضیات نبودند بلکه نیوتن در آن زمان، از طریق مشاهده و جمع‌آوری داده‌ها، به اصولی دست پیدا کرده بود که هنوز هم در طبیعت حکمفرما است. این قوانین رفتار پدیده‌های طبیعی در مورد حرکت اجسام را به خوبی و دقیق، توصیف می‌کند، بطوری که امروزه از اصول اولیه فیزیک محسوب می‌شوند.

از طرف دیگر با توجه به این اصول و قوانین دیگر احتیاجی به ایجاد جدول‌های متعدد و طویل داده‌ها در مورد وضعیت حرکت اجسام با سرعت‌ها و یا شتاب‌های مختلف نیست، زیرا این قوانین به طور کامل این رابطه‌ها را مشخص کرده‌اند. برای مثال در مورد ارتباط بین نیرو و شتاب نیوتن تابع $$F=m.a$$ را معرفی کرد. با توجه به این رابطه برای هر جسم با جرم m , شتاب a می‌توان نیرو F را محاسبه کرد و دیگر احتیاجی به انجام آزمایش و اندازه‌گیری (تولید داده‌های جدید) نیست. به این ترتیب طول داده‌های تولیدی برای مشخص کردن نیرو با توجه به این رابطه کوتاه است پس براین اساس $$Length(D|h)$$ کوچک خواهد بود.

ولی اگر داده‌ها، از فرضیاتی که در نظر گرفته‌ایم فاصله داشته باشد این طول افزایش یافته و باید برای توصیف آن‌ها از فرضیات بیشتری کمک گرفت. در نتیجه $$Length(D|h)$$ را می‌توان به عنوان میزان توصیف داده‌ها توسط فرضیه h در نظر گرفت. به این ترتیب در مورد مسائل دسته‌بندی این میزان را می‌توان «خطای دسته‌بندی» (Misclassification) یا نرخ خطا محسوب کرد. در حالتی که مدل یا فرضیات، بهترین پیش‌بینی داده‌ها را داشته باشند مقدار خطا بسیار کوچک و در حالت حدی نزدیک به صفر است و در غیر اینصورت مقدار طول $$Length(D|h)$$ بزرگ خواهد بود.

ولی در اینجا باید توازن را حفظ کرد. استفاده از مدل ساده که با «تیغ اکام» (Ockhma Razer) ایجاد شده، ممکن است همه داده‌ها را به خوبی توصیف نکند. در نتیجه باید داده‌های بیشتری را برای آموزش مدل به کار برید. از طرف دیگر استفاده از مدل پیچیده با پارامترهای زیاد (حداکثر شرط و فرضیات در مورد مدل) ممکن است برای «داده‌های آموزش» (Training Data)، خطا کوچک باشد ولی با توجه به مفهوم بی‌نظمی و اصول MAP مدل مناسبی ایجاد نشده است زیرا بی‌نظمی آن حداکثر است.

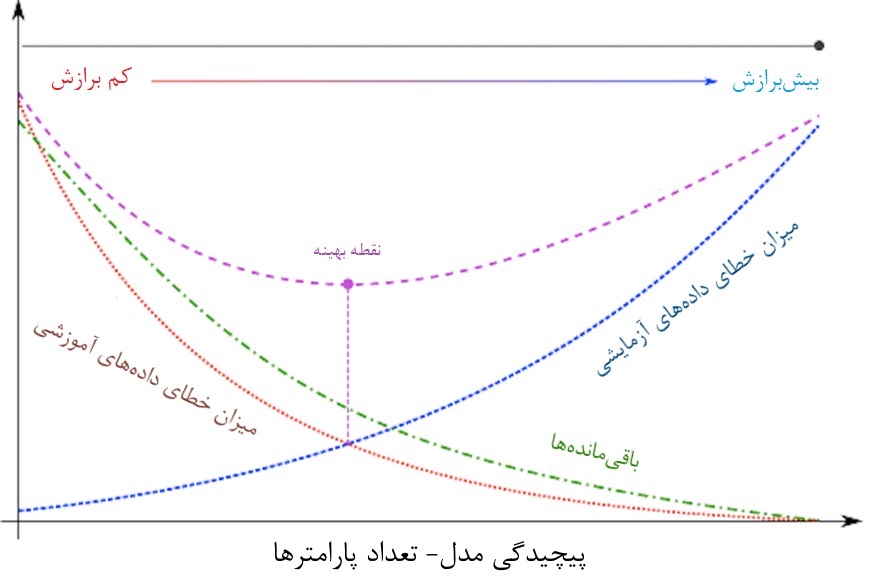
این همان مفهوم توازن و موازنه بین واریانس-اریبی یا واریانس-بایاس (Bias-Variance Trade-off) است. تصویر زیر به بررسی این وضعیت هنگام بیش‌برازش یا کم‌برازش مدل می‌پردازد.

محور افقی، میزان پیچیدگی مدل و محول عمودی نیز میزان خطا را نشان می‌دهد. با افزایش پیچیدگی مدل (افزایش تعداد پارامترهای آن) مدل بیش‌برازش شده و خطای حاصل از داده‌های آموزشی که به رنگ نارنجی نمایش داده شده، کاهش می‌یابد. ولی از طرف دیگر خطای برآورد برای داده‌هایی که در مدل  استفاده نشده‌اند (داده‌های آزمایشی) که به رنگ آبی مشخص است، افزایش می‌یابد. مجموع این و خطا روی نمودار با رنگ بنقش مشخص شده که ابتدا کاهشی و سپس افزایشی می‌شود.

در نقطه‌ای که با رنگ بنقش مشخص شده تعداد پارامترها به شکلی تعیین شده که هم اریبی (Bias) و هم واریانس (Variance) حداقل هستند. در نتیجه مدل مناسب با تعداد پارامترهای مناسب، بهترین مدل خواهد بود، زیرا نه دچار بیش‌برازش شده و نه کم‌برازش دارد. رنگ سبز باقی‌مانده ها را نشان می‌دهد که با افزایش تعداد پارامترهای مدل کاهش خواهد یافت. هر چه در نمودار از سمت چپ به سمت راست حرکت کنیم، بیش‌برازش بیشتر شده و پیچیدگی مدل نیز افزایش می‌یابد.

برای مثال فرض کنید که در حالت کم‌برازش میانگین همه داده‌ها (امید ریاضی) را به عنوان مدل توصیفی برای داده‌ها در نظر بگیریم. یعنی داشته باشیم:

$$\large y=E(Y|D)$$

یعنی مقدار پیش‌بینی برای همه داده‌های یکسان و برابر با میانگین آن‌ها است. مشخص است که واریانس در این میان صفر است (منحنی با رنگ آبی) زیرا همه مقدارهای پیش‌بینی با هم برابرند. ولی از طرف دیگر فاصله بین مقدار واقعی و مقدار پیش‌بینی زیاد (اریبی با رنگ سبز) است.

$$\large Bias=y-\overline{y}$$

برعکس زمانی که بیش‌برازش اتفاق می‌افتد به مانند این است که مدل همه مقدارهای متغیر وابسته را حفظ کرده است در نتیجه برای هر نقطه داریم:

$$\large y=\widehat{y}$$

در این حالت برای داده‌های آموزشی، مقدار برآورد $$\widehat{y}$$ همان مقدار مشاهده شده برای متغیر وابسته است. در نتیجه اریبی برابر با صفر (خط سبز) است ولی واریانس برابر با واریانس مقدارهای y (خط آبی) خواهد بود.

با انتخاب مدل با پارامترهای مناسب، به نقطه‌ای می‌رسیم که این دو خطا کمینه هستند و برعکس با انتخاب کمینه برای هر دو خطا، به نقطه‌ای می‌رسیم که تعداد پارامترهای مدل (پیچیدگی مدل) بهینه می‌شود.

تجمیع مفاهیم بیز، بی‌نظمی و تیغ اکام

براساس مطالب که در قسمت‌های قبل گفته شد، می‌توان اینطور در نظر گرفت که استنباط بیزی بهترین فرضیه (مدل) را براساس کمترین مقدار برای مجموع دو عبارت طول فرضیه (مدل) و نرخ خطا (Error Rate) در نظر می‌گیرد.

فیلم آموزش رایگان یادگیری ماشین با پایتون – سریع و آسان در ۱۸۰ دقیقه در فرادرس

کلیک کنید

این حالت در یادگیری ماشین یا «یادگیری نظارت شده» (Supervised Learning) کاربرد دارد. به بیان دیگر می‌توان براساس کمینه‌سازی مجموع این دو عبارت به سوالات مشکل زیر پاسخ داد:

• پیچیدگی مدل خطی (Linear Model)- درجه چند جمله‌ای باید چند باشد و چطور باید مجموع مربعات خطا را کاهش داد؟
• تعیین ساختار شبکه عصبی (Neural Network)- چگونه دچار بیش‌برازش نشد و در عین حال بیشترین دقت و یا کمترین خطا را در پیش‌بینی داده‌ها بدست آورد؟
• ماشین بردار پشتیان (Support Vector Machine) و انتخاب هسته (Kernel)- ایجاد توازن بین حاشیه‌های نرم و سخت (Soft Hard Margin) که به معنی تعادل بین دقت و تصمیمات مرزی غیرخطی است، چگونه انجام شود؟

نتیجه‌گیری از اصل حداقل طول (Minimum Description Length)

اصل حداقل طول یا همان MDL چه چیزی را به ما می‌گوید؟ آیا همیشه انتخاب مدل با کمترین پارامترها مناسب است؟ به طور قطع چنین نیست.

در بین چندین فرضیه‌، اگر توصیف فرض h دارای طول $$-\log_2P(h)$$ و توصیف خطاها به صورت طول داده‌ها (D) به شرط فرض (h) با طول $$-\log_2(P(D|h)$$ کدگذاری شده باشد، آنگاه استفاده از اصل MDL فرضیات MAP (بیشترین احتمال پسین) را تولید می‌کند. که با توجه به اصول بی‌نظمی دارای کمترین طول هستند. البته برای آنکه نشان دهیم به توصیف خوبی از داده‌ها دست پیدا کرده‌ایم باید همه احتمال پیشین و پسین را در نظر گرفته باشیم. بنابراین هیج دلیلی وجود ندارد که فرضیه‌ای که براساس MDL ایجاد شده است، بر همه فرضیه‌های ممکن دیگر ترجیح دارد.

در یادگیری ماشین کاربردی، گاهی نظر یک طراح و به کارگیری دانش بشری، می‌تواند توصیف بهتری برای فرضیات نسبت به احتمالات و قوانین شانس داشته باشد. به همین علت موضوع دانش و حوزه تخصصی دارای اهمیت می‌شود. به این ترتیب به جای بررسی و تحلیل تعداد بی‌شماری از فرضیات، استفاده از تخصص و دانش و تجربه بشری می‌تواند راه میانبری برای رسیدن به بهترین تصمیمات MAP باشد.

خلاصه و تفکر بیشتر

استفاده از اصول ساده ریاضیات و ترکیب آن‌ها با یکدیگر، از شیرین‌ترین و جذاب‌ترین سرگرمی‌هایی است که ریاضیدانان و فیلسوف‌ها به آن مشغول هستند و نکته جالب‌تر آن است که از نتایج حاصل از این سرگرمی‌ها در بسیاری از زمینه‌های علوم جدید مانند یادگیری نظارت شده ماشینی بهره گرفته می‌شود.

اگر مطلب بالا برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش‌های یادگیری ماشین و بازشناسی الگو
• آموزش آمار و احتمال مهندسی
• آموزش یادگیری ماشین
• آموزش یادگیری ماشین (Machine Learning) با پایتون (Python)
• احتمال شرطی (Conditional Probability) — اصول و شیوه محاسبه
• قضیه بیز در احتمال شرطی و کاربردهای آن
• تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده
• برترین الگوریتم های پیش بینی در یادگیری ماشین (Machine Learning)
• راهنمای سریع (Cheat Sheet) ارزیابی مدل در یادگیری ماشین

^^