پیاده سازی الگوریتم گرادیان کاهشی در پایتون — راهنمای گام به گام
الگوریتم گرادیان کاهشی روشی برای پیدا کردن کمینه محلی توابع است که بسیار پرکاربرد بوده و در تعداد زیادی از روشها، از آن ایده گرفته میشود. در این آموزش، با پیاده سازی الگوریتم گرادیان کاهشی در پایتون آشنا میشویم.
الگوریتم گرادیان کاهشی
به طور کلی، روش گرادیان کاهشی (Gradient Descent) بیان میکند که برای کمینه کردن یه تابع، نیاز است تا در دفعات مختلف، مقدار گرادیان را محاسبه کرده، و در جهت عکس آن حرکت کنیم.
به طور کلی، گرادیان جهتی از حرکت را بیان میکند که اگر در آن مسیر حرکت کنیم، شاهد بیشترین افزایش در مقدار تابع خواهیم بود، به همین دلیل است که به این روش گرادیان کاهشی گفته میشود.
اگر تابع $$ F (\overrightarrow {x}) $$ را در نظر بگیریم که با گرفتن بردار $$\overrightarrow {x}$$ در خروجی عدد $$y$$ را برگرداند، میتوان با شروع از $$x_0$$ به صورت زیر حرکت کرد و مقدار تابع را کمینه کرد:
$$ \large \overrightarrow {x_{n+1}}= \overrightarrow {x_n}-\eta \triangledown F ( \overrightarrow {x_n}) $$
به این ترتیب، میتوانیم جوابهای بعدی را محاسبه کنیم.
توجه داشته باشید که مقدار گرادیان در «نرخ یادگیری» (Learning Rate) ضرب میشود و سپس از مقدار $$\overrightarrow {x_n}$$ کم میشود. دلیل این اتفاق به ذات الگوریتم گرادیان کاهش برمیگردد. این الگوریتم تنها از مشتق اول تابع هدف استفاده میکند و تغییراتی که $$\overrightarrow {x_n}$$ تنها برگرفته از شیب تابع است و نمیتواند انحناهای مربوط به مشتقات درجات بالاتر را وارد رفتار خود کند. به همین دلیل، تغییراتی که در $$\overrightarrow {x_n}$$ ایجاد میکند تنها در بازه کوچکی از دقت بالایی برخوردار است. همین موضوع باعث میشود تا گام تغییرات را عدد کوچکی (از 0٫001 تا 0٫1) ضرب کنیم تا الگوریتم واگرا نشود.
برای پیدا کردن مشتق نیز میتوانیم از مشتقگیری عددی استفاده کنیم:
$$ \large F'(x)= \frac {F (x + h)-F(x-h)}{2 h} $$
برای یادگیری برنامهنویسی با زبان پایتون، پیشنهاد میکنیم به مجموعه آموزشهای مقدماتی تا پیشرفته پایتون فرادرس مراجعه کنید که لینک آن در ادامه آورده شده است.
پیاده سازی گرادیان کاهشی در پایتون
اکنون که با الگوریتم گرادیان کاهشی آشنا شدهایم، میتوانیم وارد محیط برنامهنویسی شویم.
ابتدا کتابخانههای مورد نیاز را فراخوانی میکنیم:
1import numpy as np
2import matplotlib.pyplot as pltاین کتابخانهها به ترتیب برای کار با آرایهها و رسم نمودار مورد استفاده قرار خواهند گرفت.
حال تابع هدف را تعریف میکنیم:
$$ \large f ( x ) = x ^ 2 $$
که خواهیم داشت:
1# Function to Minimize
2def f(x:float):
3 return x**2حال محل شروع الگوریتم را تعیین میکنیم:
1x0 = 3 # Initial Solutionاکنون نرخ یادگیری و تعداد مراحل کار الگوریتم را تعریف میکنیم:
1lr = 1e-2 # Learning Rate
2nIteration = 10 # Iteration Countبه این ترتیب، موارد مورد نیاز برای اجرای الگوریتم ایجاد شدند.
حال حلقه اصلی برای کار الگوریتم را ایجاد میکنیم:
1x = x0
2
3# Algorithm Main Loop
4for i in range(nIteration):
5 x = x - lr * (2 * x)توجه داشته باشید که مشتق تابع $$ f (x ) = x ^ 2 $$ بهصورت $$ f' (x) = 2 x $$ خواهد بود.
برای مشاهده روند کار الگوریتم و کوتاه کردن کدها، میتوانیم به صورت زیر عمل کنیم:
1x = x0
2
3# Algorithm Main Loop
4print(f'x{0}: {round(x, 4)} -- y{0}: {round(f(x), 4)}')
5for i in range(nIteration):
6 x -= lr * (2 * x)
7 print(f'x{i + 1}: {round(x, 4)} -- y{i + 1}: {round(f(x), 4)}')با اجرای کد خواهیم داشت:
x0: 3 -- y0: 9 x1: 2.94 -- y1: 8.6436 x2: 2.8812 -- y2: 8.3013 x3: 2.8236 -- y3: 7.9726 x4: 2.7671 -- y4: 7.6569 x5: 2.7118 -- y5: 7.3537 x6: 2.6575 -- y6: 7.0625 x7: 2.6044 -- y7: 6.7828 x8: 2.5523 -- y8: 6.5142 x9: 2.5012 -- y9: 6.2562 x10: 2.4512 -- y10: 6.0085
مشاهده میکنیم که الگوریتم بهخوبی مقدار تابع را کاهش میدهد. بهدلیل کم بودن مقدار نرخ یادگیری، الگوریتم گامهای کوچک، اما مطمئنتری برمیدارد. با افزایش نرخ یادگیری به 0٫1 خواهیم داشت:
x0: 3 -- y0: 9 x1: 2.4 -- y1: 5.76 x2: 1.92 -- y2: 3.6864 x3: 1.536 -- y3: 2.3593 x4: 1.2288 -- y4: 1.5099 x5: 0.983 -- y5: 0.9664 x6: 0.7864 -- y6: 0.6185 x7: 0.6291 -- y7: 0.3958 x8: 0.5033 -- y8: 0.2533 x9: 0.4027 -- y9: 0.1621 x10: 0.3221 -- y10: 0.1038
به این ترتیب، سرعت کمینهسازی بالاتر میرود و الگوریتم در تعداد مراحل ثابت، به میزان بیشتر بهبود ایجاد میکند.
حال تابع مشتق عددی را تعریف میکنیم:
1# Numerical Derivative
2def Derivative(Function, x:float, h:float=1e-6):
3 d = (Function(x + h) - Function(x - h)) / (2 * h)
4 return dبا استفاده از این تابع، میتوانیم مشتق توابع مختلف را بدون نیاز به مشتقگیری محاسبه کنیم.
حال تابع را در حلقه نوشته شده جایگذاری میکنیم:
1 x -= lr * Derivative(f, x)به این ترتیب الگوریتم تکمیل میشود.
برای مشاهده روند کار الگوریتم نیز میتوانیم نمودار تابع را رسم کرده و مقدار x را در مراحل محتلف نمایش دهیم.
برای این کار، ابتدا یک لیست خالی برای اضافه کردن مقدار x و y در هر مرحله ایجاد میکنیم:
1xSolution = []
2ySolution = []
3
4x = x0
5
6xSolution.append(x)
7ySolution.append(f(x))
8
9# Algorithm Main Loop
10for i in range(nIteration):
11 x -= lr * Derivative(f, x)
12 xSolution.append(x)
13 ySolution.append(f(x))به این ترتیب مقدار x و y در طول کار الگوریتم ذخیره میشود.
حال نیاز داریم تا نمودار تابع هدف را نیز رسم کنیم. برای این کار میتوانیم از numpy به شکل زیر استفاده کنیم:
1Xs = np.linspace(-3, +3, num=51)
2Ys = np.vectorize(f)(Xs)حال برای رسم نمودار خواهیم داشت:
1plt.plot(Xs, Ys, lw=1, c='teal', label='Function Label')
2plt.plot(xSolution, ySolution, lw=0.8, marker='o', ms=3, c='crimson', label='Points Over Iterations')
3plt.xlabel('x')
4plt.ylabel('y')
5plt.legend()
6plt.show()پس از اجرا، به نمودار زیر میرسیم.
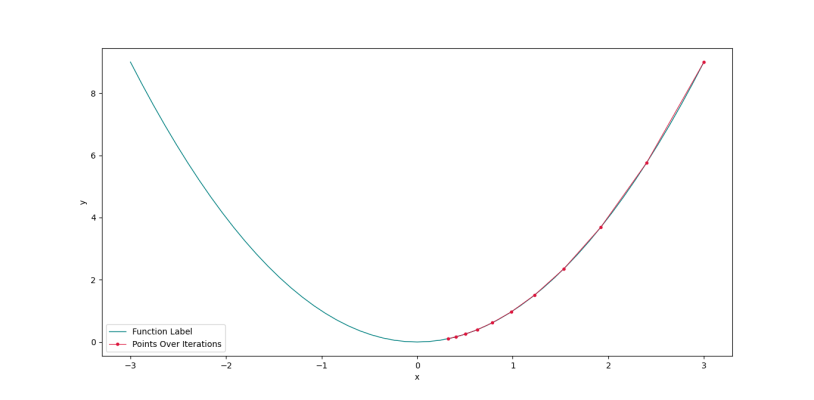
به این ترتیب، مشاهده میکنیم که الگوریتم در جهت کاهش مقدار تابع به خوبی درحال حرکت است. توجه داشته باشید اندازه گام با نزدیک شدن به محل کمینه، کوچکتر میشود که به دلیل کوچک شدن مقدار گرادیان است.
حال اگر مقدار نرخ یادگیری با به 0٫9 افزایش دهیم، به نمودار زیر میرسیم.
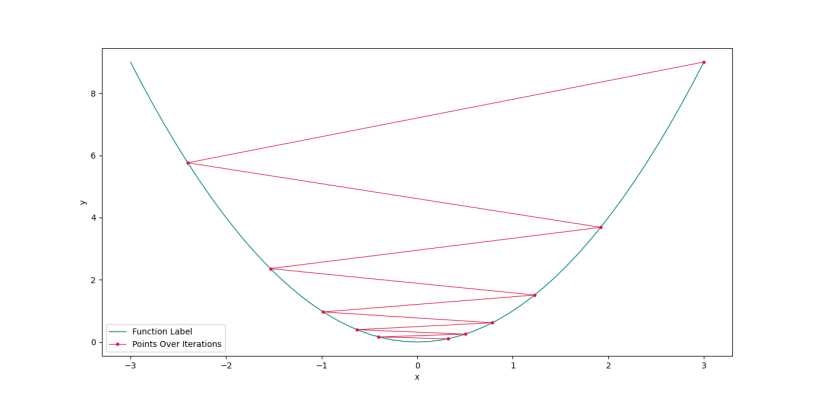
در این شرایط، با وجود اینکه مقدار نرخ یادگیری نامناسب است، اما الگوریتم میتواند همگرا شود.
اگر از نقطه $$x_0=1$$ شروع کنیم و نرخ یادگیری برابر با 1٫05 باشد، شکل زیر را خواهیم داشت.
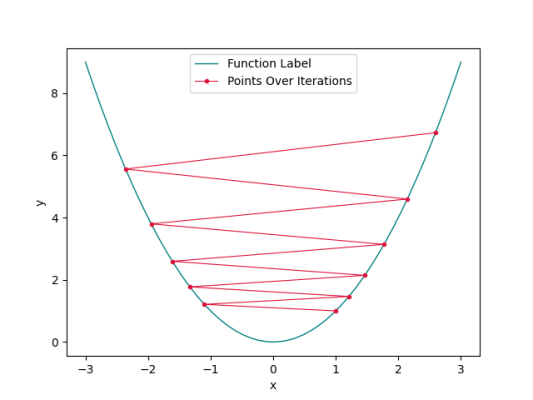
به این ترتیب، مشاهده میکنیم که الگوریتم واگرا میشود.
بنابراین، میتوان نتیجه گرفت که با تغییر نرخ یادگیری، یکی از چهار حالت زیر رخ خواهد داد:
- نرخ یادگیری بسیار کوچک باشد: الگوریتم با اطمینان زیادی در جهت درست حرکت میکند، اما سرعت کمینهسازی پایین است.
- نرخ یادگیری مناسب باشد: الگوریتم با اطمینان مناسب، در زمان معقولی به کمینه محلی میرسد.
- نرخ یادگیری بزرگتر از مقدار مناسب باشد: الگوریتم با اینکه رفتار ناپایداری دارد، همچنان میتواند به کمینه محلی نزدیک شود.
- نرخ یادگیری بسیار بزرگ باشد: الگوریتم واگرا میشود و نمیتواند کمینهسازی انجام دهد.
توابعی با بیش از یک ورودی
حال میتوانیم توابعی با بیش از یک ورودی را بررسی کنیم.
تابع روزن بروک تابعی معروف برای بررسی عملکرد الگوریتمهای بهینهساز است که به صورت زیر تعریف میشود:
$$ \large f ( x _ 1 , x _ 2 ) = ( 1 - x _1 )^2+100(x_2-x_1^2)^2 $$
این تابع در محل $$ x = (1 , 1 )$$ به کمینه میرسد.
برای این منظور، ابتدا تابع تعریفشده را اصلاح میکنیم:
1# Function to Minimize
2def f(x:np.ndarray):
3 return (1-x[0])**2 + 100 * (x[1] - x[0]**2)**2توجه داشته باشید که چون بیش از یک پارامتر وجود دارد، باید از آرایهها استفاده کنیم.
حال تابع مشتق را اصلاح میکنیم:
1# Gradient
2def Gradient(Function, x:np.ndarray, h:float=1e-6):
3 nX = x.size
4 g = np.zeros(nX)
5 fx = Function(x)
6 for i in range(nX):
7 temp = x.copy()
8 temp[i] += h
9 ftemp = Function(temp)
10 g[i] = (ftemp - fx) / h
11 return gدر این تابع به ترتیب عملیات زیر رخ میدهد:
- ابتدا ورودیها از جمله هدف، محل مشتقگیری و مقدار گام دریافت میشود.
- تعداد پارامترها تعیین میشود.
- یک آرایه خالی برای ذخیره مشتق تابع نسبت به هر پارامتر ایجاد میشود.
- مقدار تابع در محل مشتقگیری محاسبه و ذخیره میشود.
- داخل حلقه بهازای هر پارامتر:
a. یک نسخه کپی از x ایجاد میشود.
b. پارامتر انتخاب شده در حلقه بهاندازه گام افزایش مییابد.
c. مقدار تابع در موقعیت فعلی محاسبه میشود.
d. مقدار مشتق حساب شده و به آرایه گرادیان اضافه میشود. - آرایه گرادیان خروجی داده میشود.
حال محل شروع، نرخ یادگیری و تعداد مراحل را تعریف میکنیم:
1x0 = np.array([0.1, 0.1]) # Initial Solution
2lr = 2e-3 # Learning Rate
3nIteration = 90 # Iteration Countو برای تعریف حلقه اصلی برنامه خواهیم داشت:
1x = x0
2print(f'y{0}: {round(f(x), 4)}')
3# Algorithm Main Loop
4for i in range(nIteration):
5 x -= lr * Gradient(f, x)
6 print(f'y{i+1}: {round(f(x), 4)}')که با اجرا به ترتیب مقادیر زیر بهدست میآید:
y0: 1.62 y1: 1.0582 y2: 0.8613 y3: 0.7907 y4: 0.7632 y5: 0.7502 y6: 0.7422 y7: 0.7359 y8: 0.7302 y9: 0.7248
حال میتوانیم برنامه خود با اندکی ارتقا داده و الگوریتم گرادیان کاهشی را به شکل یک تابع تعریف کنیم:
1# Gradient Descent Algorithm
2def GDA(Function, x0:np.ndarray, nIteration:int, lr:float=1e-3):
3 x = x0
4 for _ in range(nIteration):
5 x -= lr * Gradient(Function, x)
6 return xبه این ترتیب الگوریتم گرادیان کاهشی در پایتون تعریف میشود.
جمعبندی
در این آموزش از مجله فرادرس، با الگوریتم گرادیان کاهشی آشنا شدیم. همچنین، روش گام به گام پیاده سازی الگوریتم گرادیان کاهشی در پایتون را بیان کردیم.










