چندجمله ای های متعامد — از صفر تا صد (+ دانلود فیلم آموزش رایگان)

چندجمله‌ای‌های متعامد (Orthogonal Polynomials) دنباله‌ای نامتناهی از چندجمله‌ای‌های عمود بر هم هستند. در این آموزش با چندجمله ای های متعامد آشنا می‌شویم.

چندجمله‌ ای‌ های متعامد

چندجمله‌‌ای‌‌های $$p(x)$$ و $$q(x)$$ که روی بازه $$\left[ {a,b} \right]$$ تعریف شده‌‌اند، متعامد هستند، هرگاه

$$ \large { \int \limits _ a ^ b { p \left ( x \right ) q \left ( x \right ) w \left ( x \right ) d x } } = { 0 , } $$

که در آن، $${w\left( x \right)}$$ تابع وزن غیرمنفی است.

دنباله چندجمله‌‌ای $${p_n}\left( x \right)$$ ($$n = 0,1,2, \ldots$$) که در آن $$n$$ مرتبه $${p_n}\left( x \right)$$ است را دنباله‌‌ای از چندجمله‌‌ای‌‌های متعامد می‌‌گویند، هرگاه:

$$ \large { \int \limits _ a ^ b { { p _ m } \left ( x \right ){ p _ n } \left ( x \right ) w \left ( x \right ) d x } } = { { c _ n } { \delta _ { m n } } , } $$

که در آن، $$c_n$$ ثابت‌‌های تعیین شده و $${\delta _{mn}}$$ دلتای کرونکر است.

سری فوریه تعمیم‌ یافته

سری فوریه تعمیم‌ یافته، بسط سری یک تابع بر اساس دستگاهی از چندجمله‌‌ای‌‌های متعامد است. با استفاده از این تعامد، تابع تکه‌‌ای پیوسته $$f(x)$$ می‌‌تواند به صورت بسط سری فوریه تعمیم‌ یافته بیان شود:

$$ \large { \sum \limits _ { n = 0 } ^ \infty { { c _ n } { p _ n } \left ( x \right ) } \text { = }} \kern0pt
{ \begin {cases}
f \left ( x \right ) , \; \text {if}\, f \left ( x \right ) \,\text {is continuous} \\
\frac { { f \left ( { x – 0 } \right ) + f \left ( { x + 0 } \right ) } } { 2 } , \; \text {at a jump discontinuity}
\end {cases}} $$

در ادامه به بررسی چهار نوع از چندجمله‌‌ای‌‌های متعامد شامل چندجمله‌‌های هرمیت، لاگر، لژاندر و چبیشف می‌‌پردازیم.

چند جمله‌‌ای‌‌های هرمیت

چندجمله‌‌ای‌‌های هرمیت $$ {H_n}\left( x \right) ={\left( { – 1} \right)^n}{e^{{x^2}}}{\large\frac{{{d^n}}}{{d{x^n}}}\normalsize} {e^{ – {x^2}}} $$ روی بازه $$\left( { – \infty ,\infty } \right)$$ نسبت به تابع وزن $${e^{ – {x^2}}}$$ متعامد هستند:

$$ \large { \int \limits _ { – \infty } ^ \infty { { e ^ { – { x ^ 2 } } } { H _ m } \left ( x \right ) { H _ n } \left ( x \right ) d x } } =
{ \begin {cases}
0 , & m \ne n \\
{ 2 ^ n } n ! \sqrt \pi , & m = n
\end {cases} . } $$

در تعریف دیگری، از تابع وزن $${e^{ – \frac{{{x^2}}}{2}}}$$ استفاده می‌‌شود. در برخی موارد، این تعریف در نظریه احتمال ترجیح داده می‌‌شود، زیرا $${\large\frac{1}{{\sqrt {2\pi } }}\normalsize} {e^{ – \frac{{{x^2}}}{2}}}$$ تابع چگالی احتمال برای توزیع نرمال است.

چند جمله‌‌ای‌‌های لاگر

این نوع چندجمله‌‌ای‌‌ها که به صورت $$ {L_n}\left( x \right) ={\large\frac{{{e^x}}}{{n!}}\normalsize} {\large\frac{{{d^n}\left( {{x^n}{e^{ – x}}} \right)}}{{d{x^n}}}\normalsize}, n = 0,1,2,3, \ldots $$ تعریف می‌‌شوند، روی بازه $$\left( {0,\infty } \right)$$ با تابع وزن $${{e^{ – x}}}$$ متعامدند:

$$ \large { \int \limits _ 0 ^ \infty { { e ^ { – x } } { L _ m } \left ( x \right ) { L _ n } \left ( x \right ) d x } } =
{ \begin {cases}
0 , & m \ne n \\
1 , & m = n
\end {cases}.} $$

چند جمله‌‌ای‌‌های لژاندر

چندجمله‌‌ای‌‌های لژاندر $${P_n}\left( x \right) ={\large\frac{1}{{{{2^n}n!}}\normalsize} {\large\frac{{{d^n}{{\left( {{x^2} – 1} \right)}^n}}} {d{x^n}}}\normalsize},n = 0,1,2,3, \ldots $$ روی بازه $$\left[ {-1,1} \right]$$ متعامد هستند:

$$ \large { \int \limits _ { – 1 } ^ 1 { { P _ m } \left ( x \right ){ P _ n } \left ( x \right ) d x } } =
{ \begin {cases}
0 , & m \ne n \\
\frac { 2 } { { 2 n + 1 } } , & m = n
\end {cases} . } $$

چند جمله‌‌ای‌‌های چبیشف

چندجمله‌‌ای‌‌های چبیشف نوع اول $$ {T_n}\left( x \right)= \cos \left( {n\arccos x} \right) $$ روی بازه $$\left[ {-1,1} \right]$$ با تابع وزن $${\large\frac{1}{{\sqrt {1 – {x^2}} }}\normalsize} $$ متعامد هستند:

$$ \large { \int \limits _ { – 1 } ^ 1 { \frac { { { T _ m } \left ( x \right ) { T _ n } \left ( x \right ) } } { { \sqrt { 1 – { x ^ 2 } } } } d x } } =
{ \begin {cases}
0 , & m \ne n \\
\pi , & m = n = 0 \\
\frac { \pi } { 2 } , & m = n \ne 0
\end {cases}.}\\ $$

مثال‌ها

در این بخش، مثال‌هایی را درباره چندجمله‌ای‌های متعامد ارائه می‌کنیم.

مثال ۱

نشان دهید که مجموعه توابع زیر روی بازه $$\left[ { – \pi ,\pi } \right]$$ متعامدند.

$$ \large { { I _ 1 } = \int \limits _ { – \pi } ^ \pi { \sin m x \sin n x d x } , \; \; \; } \kern-0.3pt \\ \large { { I _ 2 } = \int \limits _ { – \pi } ^ \pi { \cos m x \cos n x d x } , \; \; \; } \kern-0.3pt \\ \large { { I _ 3 } = \int \limits _ { – \pi } ^ \pi { \sin m x \cos n x d x } . } $$

حل: ابتدا باید انتگرال‌‌های زیر را تعیین کنیم:

$$ \large { { I _ 1 } = \int \limits _ { – \pi } ^ \pi { \sin m x \sin n x d x } } = { { \frac { 1 } { 2 } \int \limits _ { – \pi } ^ \pi { \Big [ { \cos \left ( { m x – n x } \right ) } } } } - { { { { \cos \left ( { m x + n x } \right ) } \Big] d x } } } \\ \large = { { \frac { 1 } { 2 } \int \limits _ { – \pi } ^ \pi { \Big[ { \cos \left ( { m – n } \right ) x } } } } - { { { { \cos \left ( { m + n } \right ) x } \Big] d x } } } = { \frac { 1 } { 2 } \Big[ { \left . { \Big ( { \frac { { \sin \left ( { m – n } \right ) x } } { { m – n } } } } \right . } - { \left . { { \frac { { \sin \left ( { m + n } \right ) x } } { { m + n } } } \Big ) } \right | _ { – \pi } ^ \pi } \Big ] } $$

انتگرال اول برابر است با:

$$ \large { { I _ 1 } \text { = }} \kern0pt { \frac { { \sin \left ( { m – n } \right ) \pi } } { { m – n } } – \frac { { \sin \left ( { m + n } \right ) \pi } } { { m + n } } } = { 0 . } $$

برای حالت $$m \ne n$$:

$$ \large { { I _ 1 } = \int \limits _ { – \pi } ^ \pi { { { \sin } ^ 2 } x d x } } = { \frac { 1 } { 2 } \int \limits _ { – \pi } ^ \pi { \left ( { 1 – \cos 2 n x } \right ) d x } } = { \frac { 1 }{ 2 } \left [ { \left . { \left ( { x – \frac { { \sin 2 n x } } { { 2 n } } } \right ) } \right | _ { – \pi } ^ \pi } \right ] }\\ \large = { { \frac { 1 } { 2 } \left [ { \pi – \frac { { \sin 2 n \pi } } { { 2 n } } – \left ( { – \pi } \right ) } \right . } } - { { \left . { \frac { { \sin \left ( { – 2 n \pi } \right ) } } { { 2 n } } } \right ] } } = { \pi . } $$

و برای حالت $$m=n$$، داریم:

$$ \large { { I _ 1 } } = { \int \limits _ { – \pi } ^ \pi { \sin mx\sin n x d x } } = { \begin {cases} 0 , & m \ne n \ \pi, & m = n \end {cases} . } $$

بنابراین:

$$ \large { { I _ 2 } } = { \int \limits _ { – \pi } ^ \pi { \cos mx \cos n x d x } } =
{ \begin {cases}
0, & m \ne n \\
\pi, & m = n
\end {cases},} $$

به طور مشابه، می‌‌توان انتگرال‌‌های دوم و سوم را به دست آورد:

$$ \large { { I _3 } } = { \int \limits _ { – \pi } ^ \pi { \sin m x \cos n x d x } } =
{ \begin {cases}
0, & m \ne n \\
\pi , & m = n
\end {cases} . } $$

این بدین معنی است که مجموعه توابع زیر روی بازه $$\left[ { – \pi ,\pi } \right]$$ دستگاه متعامد تشکیل می‌‌دهند:

$$ \large { 1 , \cos x , \sin x , \cos 2 x , \sin 2 x , \ldots , \; } \kern-0.3pt { \cos m x , \sin m x , \ldots } $$

مثال ۲

بسط سری فوریه-هرمیت تابع درجه دوم $$ f\left( x \right) =A{x^2} + Bx + C $$ را به دست آورید.

حل: در اینجا از جملات صریح چندجمله‌‌ای‌‌های هرمیت استفاده می‌‌کنیم:

$$ \large { { H _ 0 } \left ( x \right ) = 1 , \; \; \; } \kern-0.3pt { { H _ 1 } \left ( x \right ) = 2 x , \; \; \; } \kern-0.3pt {{ H _2 } \left ( x \right ) = 4 { x ^ 2 } – 2 . } $$

سپس، روش ضرایب نامعین را به کار می‌‌بریم:

$$ \large { A { x ^ 2 } + B x + C } = { { c _ 0 } { H _ 0 } \left ( x \right ) } + { { c _ 1 } { H _ 1 } \left ( x \right ) } + { { c _ 2 } { H _ 2 } \left ( x \right ) . } $$

با جایگذاری چندجمله‌‌ای‌‌های هرمیت و برابر قرار دادن ضرایب، داریم:

$$ \large { { A { x ^ 2 } + B x + C } = { { c _ 0 } \cdot 1 } + { { c _ 1 } \cdot 2 x } + { { c _ 2 } \cdot \left ( { 4 { x ^ 2 } – 2 } \right ) , \; \; } } \\ \large \Rightarrow { { A { x ^ 2 } + B x + C } = { { c _ 0 } + 2 { c _ 1 } x } } + { { 4 { c _ 2 } { x ^ 2 } – 2 { c _ 2 } , \; \; } } \\ \large \Rightarrow { \left\{ { \begin {array}{* { 2 0 } { l } } { 4 { c ^ 2 } = A } \\ { 2 { c _ 1 } = B } \\ {{ c _ 0 } – 2 { c _ 2 } = C } \end {array} } \right.,\;\; } \Rightarrow { { c _ 0 } = C + \frac { A } { 2 } , \; \; } \kern-0.3pt{ { c _ 1 } = \frac { B } { 2 } , \; \; } \kern-0.3pt { { c _ 2 } = \frac { A } { 4 } .} $$

بنابراین، بسط سری فوریه-هرمیت تابع مفروض به صورت زیر خواهد بود:

$$ \large { f \left ( x \right ) = A { x ^ 2 } + B x + C } = { \left ( { C + \frac { A } { 2 } } \right ) { H _ 0 } \left ( x \right ) } + { \frac { B } { 2 } { H _ 1 } \left ( x \right ) } + { \frac { A } { 4 }{ H _ 2 } \left ( x \right ) . } $$

مثال ۳

بسط سری فوریه-لاگر تابع توانی $$f\left( x \right) = {x^p},p \ge 1 $$ را بیابید.

حل: این بسط با فرمول زیر بیان می‌‌شود:

$$ \large f \left ( x \right ) = \sum \limits _ { n = 0 } ^ \infty { { c _ n } { L _ n } \left ( x \right ) } . $$

ابتدا ضرایب $$c_n$$ را به دست می‌‌آوریم:

$$ \large { { c _ 0 } = \int \limits _ 0 ^ \infty { f \left ( x \right ) { e ^ { – x } } d x } } = { \int \limits _ 0 ^ \infty { { x ^ p }{ e ^ { – x } } d x } } = { \Gamma \left ( { p + 1 } \right ) } = { p ! , } $$

که در آن، $$\Gamma$$ تابع گاماست.

به ازای $$n \ge 1$$ داریم:

$$ \large { { c _ n } = \frac { 1 } { { n ! } } \int \limits _ 0 ^ \infty { { x ^ p } \frac { { { d ^ n } \left ( { { x ^ n } { e ^ { – x } } } \right ) } } { { d { x ^ n } } } d x } }
\\ \large = { \frac { 1 } {{ n ! } } \Big [ { \left. { \left ( { { x ^ p } \frac { { { d ^ { n – 1 } } \left ( { { x ^ n } { e ^ { – x } } } \right ) } } { { d { x ^ { n – 1 } } } } } \right ) } \right | _ 0 ^ \infty } } - { { \int \limits _ 0 ^ \infty { p { x ^ { p – 1 } } \frac { { { d ^ { n – 1 } } \left ( { { x ^ n } { e ^ { – x } } } \right ) } } { { d { x ^ { n – 1 } } } } d x } } \Big ] . } $$

برای حل این انتگرال از روش جزء به جزء استفاده می‌‌کنیم. خواهیم داشت:

$$ \large { { c _ n } \text { = } } \kern0pt { { \frac { { { { \left ( { – 1 } \right ) } ^ n } } } { { n ! } } p \left ( { p – 1 } \right ) \left ( { p – 2 } \right ) \cdots } } \kern0pt{{ \left ( { p – n + 1 } \right ) \int \limits _ 0 ^ \infty { { x ^ p } { e ^ { – x } } d x } } } \\ \large
= { \frac { { { { \left ( { – 1 } \right ) } ^ n } } } { { n ! } } \cdot \frac { { p ! } } { { \left ( { p – n } \right ) ! } } \cdot \Gamma \left ( { p + 1 } \right ) }
= { \frac { { { { \left ( { – 1 } \right ) } ^ n } { { \left ( {p ! } \right ) } ^ 2 } } } { { n ! \left ( { p – n } \right ) ! } } , \; \; } \kern-0.3pt
{\text {if} \;\;1 \le n \le p.} $$

اگر $$n \gt p$$ باشد، آنگاه $${c_n} = 0$$.

بنابراین، بسط سری فوریه-لاگر تابع توانی $$f\left( x \right) = {x^p}$$ به صورت زیر بیان می‌‌شود:

$$ \large { f \left ( x \right ) = { x ^ p } } <
= { p ! } + { \sum \limits _ { n = 1 } ^ p { \frac { { { { \left ( { – 1 } \right ) } ^ n } { { \left ( { p ! } \right ) } ^ 2 } } } { { n ! \left ( { p – n } \right ) ! } } { L _ n } \left ( x \right ) } . } $$

از آنجایی که $${L_0}\left( x \right) = 1$$ است، بسط به دست آمده را می‌‌توان به صورت زیر نوشت:

$$ \large { f \left ( x \right ) = { x ^ p } }
= { \sum \limits _ { n = 0 } ^ p { \frac { { { { \left ( { – 1 } \right ) } ^ n } { { \left ( { p ! } \right ) } ^ 2 } } } { { n ! \left ( { p – n } \right ) ! } } { L _ n } \left ( x \right ) } . } $$

بسط حاصل را به ازای $$p=2$$ بررسی می‌‌کنیم:

$$ \large { { { x ^ 2 } } = { \sum \limits _ { n = 0 } ^ 2 { \frac { { { { \left ( { – 1 } \right ) } ^ n } { { \left ( { 2 ! } \right ) } ^ 2 } } } { { n ! \left ( { 2 – n } \right ) ! } } { L _ n } \left ( x \right ) } } } = { { 2 { L _ 0 } \left ( x \right ) } - { 4 { L _ 1 } \left ( x \right ) } + { 2 { L _ 2 } \left ( x \right ) . } } $$

با جایگذاری چندجمله‌‌ای‌‌های لاگرِ

$$ \large { { L _ 0 } \left ( x \right ) = 1 , \; \; \; } \kern-0.3pt{ { L _ 1 } \left ( x \right ) = 1 – x , \; \; \; } \kern-0.3pt { { L _ 2 } \left ( x \right ) = 1 – 2 x + \frac { { { x ^ 2 } } } { 2 } } $$

در فرمول بالا داریم:

$$ \large { { x ^ 2 } }
= { 2 \cdot 1 – 4 \left ( { 1 – x } \right ) } + { 2 \left ( { 1 – 2 x + \frac {{ { x ^ 2 } } } { 2 } } \right ) }
{ \equiv { x ^ 2 } . } $$

مثال ۴

بسط سری فوریه-لاگرانژ تابع پله‌‌ای زیر را به دست آورید.

$$ \large {f\left( x \right) }=
{\begin{cases}
0, & -1 \lt x \lt 0 \\
1, & 0 \lt x \lt 1
\end{cases}.} $$

حل: بسط این سری به صورت زیر نوشته می‌‌شود:

$$ \large f \left ( x \right ) = \sum \limits _ { n = 0 } ^ \infty { {c _ n } { P_ n } \left ( x \right ) } . $$

با قرار دادن جملات صریح چندجمله‌‌ای‌‌های لاگرانژ، داریم:

$$ \large { f \left ( x \right ) } = { \frac { { 2 n + 1 } }{ 2 } \int \limits _ { – 1 } ^ 1 { f \left ( x \right ) { P _ n } \left ( x \right ) d x } }
= { \frac { { 2 n + 1 } } { 2 } \int \limits _ 0 ^ 1 { { P _ n } \left ( x \right ) d x } }\\ \large
= { { \frac { { 2 n + 1 } } { 2 } } \kern0pt \int \limits _0 ^ 1 { \frac { 1 } { { { 2 ^ n } n ! } } \frac { { { d ^ n } { { \left ( { { x ^ 2 } – 1 } \right ) } ^ n } } } { { d { x ^ n } } } d x } } \\ \large
= { { \frac { { 2 n + 1 } } { { { 2 ^ { n + 1 } } n ! } } } \kern0pt \left[ { \left. { \left ( { \frac { { { d ^ { n – 1 } } { { \left ( { { x ^ 2 } – 1 } \right ) } ^ n } } } { { d { x ^ { n – 1 } } } } } \right ) } \right| _ 0 ^ 1 } \right ] , \; \; } \kern-0.3pt
{ n = 1 , 2 , 3 , \ldots } $$

اکنون ضرایب $$c_n$$ را محاسبه می‌‌کنیم. از آنجایی که $${P_0}\left( x \right) = 1$$ است، خواهیم داشت:

$$ \large { { c _ 0 } } = { \frac { 1 } { 2 } \int \limits _ { – 1 } ^ 1 { f \left ( x \right ) { P _ 0 } \left ( x \right ) d x } } = { \frac { 1 } { 2 } \int \limits _ 0 ^ 1 { d x } } = { \frac { 1 } { 2 } . } $$

سپس، مقدار مشتق $${\left. {\left( {\large\frac{{{d^{n – 1}}{{\left( {{x^2} – 1} \right)}^n}}}{{d{x^{n – 1}}}}\normalsize} \right)} \right|_0^1}$$ را تعیین می‌‌کنیم تا ضرایب $$c_n$$ به ازای $$n \ge 1$$ به دست آیند.

بدیهی است که این عبارت در $$x=1$$ به ازای $$n \ge 1$$ برابر با صفر است. برای به دست آوردن مقدار این مشتق در نقطه $$x=0$$، از فرمول دوجمله‌‌ای نیوتن استفاده می‌‌کنیم:

$$ \large { \frac { { { d ^ { n – 1 } } { { \left ( { { x ^ 2 } – 1 } \right ) } ^ n } } } { { d { x ^ { n – 1 } } } } }
= { \frac { { d { { \left ( { \sum \limits _ { m = 0 } ^ \infty { C _ n ^ m { { \left ( { – 1 } \right ) } ^ m } { x ^ { 2 n – 2 m } } } } \right ) } ^ { n – 1 } } } } { { d { x ^ { n – 1 } } } } } \\ \large
= { \sum \limits _ { m = 0 } ^ { m \le \frac { { n + 1 } } { 2 } } { \left [ { C _ n ^ m { { \left ( { – 1 } \right ) } ^ m } \left ( { 2 n – 2 m } \right ) \cdot } \right . } } \kern0pt { { \left . { \left ( { 2 n – 2 m – 1 } \right ) } \right . } } \kern0pt
{ \cdots \left . { \left ( { – 2 m + n + 2 } \right ) { x ^ { n – 2 m + 1 } } } \right ] . } $$

همانطور که می‌‌بینیم، این جمع در $$x=0$$ به ازای اعداد زوج $$ n = 2k,k = 0,1,2,3, \ldots $$ صفر و به ازای اعداد فرد برابر است با:

$$ \large { C _ { 2 k + 1 } ^ { k + 1 } { \left ( { – 1 } \right ) ^ { k + 1 } } 2 k \left ( { 2 k – 1 } \right ) \cdot } \kern0pt{ \left ( { 2 k – 2 } \right ) \cdots 3 \cdot 2 } = { C _ { 2 k + 1 } ^ { k + 1 } { \left ( { – 1 } \right ) ^ { k + 1 } } \left ( { 2 k } \right ) ! } $$

هنگامی که $$x \to 0$$، به ازای $$n = 2k + 1$$ و $$m = k + 1$$، $$ {x^{n – 2m + 1}} = {x^{2k + 1 – 2\left( {k + 1} \right) + 1}}= {x^0} =1 $$ است. برای سایر مقادیر $$m$$ و $$n$$، این جملات برابر با صفر هستند. از این رو:

$$ \large { c _ { 2 k } } = 0 , $$

$$ \large { { c _ { 2 k + 1 } } } = { \frac { { 4 k + 3 } }{ { { 2 ^ { 2 k + 2 } } \left ( { 2 k + 1 } \right ) ! } } \cdot } \kern0pt{ \frac { { \left ( { 2 k + 1 } \right ) ! } } { { \left ( { k + 1 } \right ) ! k ! } } { \left ( { – 1 } \right ) ^ k } \left ( { 2 k } \right ) ! } = { \frac { { { { \left ( { – 1 } \right ) } ^ k } \left ( { 4 k + 3 } \right ) \left ( { 2 k } \right ) ! } } { { { 2 ^ { 2 k + 2 } } \left ( { k + 1 } \right ) ! k ! } } . } $$

بنابراین، بسط سری فوریه-لاگرانژ این تابع به صورت زیر خواهد بود:

$$ \large { f \left ( x \right ) } = { \frac { 1 } { 2 } \text { + }} \kern0pt { \sum \limits _ { k = 0 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ k } \left ( { 4 k + 3 } \right ) \left ( { 2 k } \right ) ! } } { { { 2 ^ { 2 k + 2 } } \left ( { k + 1 } \right ) ! k ! } } \cdot } \kern0pt { { P _ { 2 k + 1 } } \left ( x \right ) } . } $$

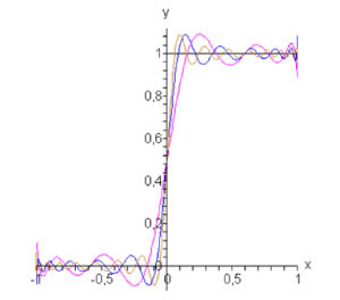
در شکل زیر، تقریب این تابع پله‌‌ای با استفاده از سری فوریه-لاگرانژ به ازای $$ n=5,10,155$$ نشان داده شده است.

مثال ۵

بسط سری فوریه-چبیشف تابع $$f\left( x \right) = {x^3}$$ را روی بازه $$\left[ { – 1,1} \right]$$ بیابید.

حل: بسط سری فوریه-چبیشف این تابع به صورت زیر نمایش داده می‌‌شود:

$$ \large { { x ^ 3 } = \sum \limits _ { n = 0 } ^ \infty { { c _ n } { T _ n } \left ( x \right ) } } = { { c _ 0 } + \sum \limits _ { n = 1 } ^ \infty { { c _ n } { T _ n } \left ( x \right ) } . } $$

برای محاسبه ضرایب $$c_n$$، از خاصیت تعامد چندجمله‌‌ای‌‌های چبیشف روی بازه $$\left[ { – 1,1} \right]$$ با تابع وزن $${\large\frac{1}{{\sqrt {1 – {x^2}} }}\normalsize}$$ استفاده می‌‌کنیم.

با ضرب $$\large\frac{1}{{\sqrt {1 – {x^2}} }}\normalsize $$ در دو طرف بسط فوق و انتگرال‌‌گیری روی بازه $$\left[ { – 1,1} \right]$$، داریم:

$$ \large { \int \limits _ { – 1 } ^ 1 { \frac { { { x ^ 3 } d x } }{ { \sqrt { 1 – { x ^ 2 } } } } } } = { \int \limits _ { – 1 } ^ 1 { \left ( { \sum \limits _ { n = 0 } ^ \infty { { c _ n } { T _ n } \left ( x \right ) } } \right ) \frac { { d x } } { { \sqrt { 1 – { x ^ 2 } } } } } . } $$

از آنجایی که $$f\left( x \right) = {x^3}$$ تابعی فرد است و روی بازه متقارن $$\left[ { – 1,1} \right]$$ انتگرال می‌‌گیریم، انتگرال طرف چپ برابر با صفر است:

$$ \large \int \limits _ { – 1 } ^ 1 { \frac { { { x ^ 3 } d x } }{ { \sqrt { 1 – { x ^ 2 } } } } } = 0 . $$

انتگرال طرف راست را می‌‌توان این‌گونه نوشت:

$$ \large { \int \limits _ { – 1 } ^ 1 { \left ( { \sum \limits _ { n = 0 } ^ \infty { { c _ n } { T _ n } \left ( x \right ) } } \right ) \frac { { d x } } { { \sqrt { 1 – { x ^ 2 } } } } } }
= { \int \limits _ { – 1 } ^ 1 { \left ( { { c _ 0 } + \sum \limits _ { n = 1 } ^ \infty { { c _ n } { T _ n } \left ( x \right ) } } \right ) \frac { { d x } } { { \sqrt { 1 – { x ^ 2 } } } } } }\\ \large
= { { c _ 0 } \int \limits _ { – 1 } ^ 1 { \frac { { d x } } { { \sqrt { 1 – { x ^ 2 } } } } } } + { \sum \limits _ { n = 1 } ^ \infty { \left [ { { c _ n } \int \limits _ { – 1 } ^ 1 { \frac { { { T _ n } \left ( x \right ) } } { { \sqrt { 1 – { x ^ 2 } } } } d x } } \right ] } . } $$

با ضرب $${T_0}\left( x \right) = 1$$ در عبارت زیر انتگرال دوم و با توجه به متعامد بودن چندجمله‌‌ای‌‌های چبیشف، خواهیم داشت:

$$ \large \int \limits _ { – 1 } ^ 1 { \frac { { { T _ n } \left ( x \right ) { T _ 0 } \left ( x \right ) } } { { \sqrt { 1 – { x ^ 2 } } } } d x } = 0 $$

بنابراین:

$$ \large { c _ 0 } \int \limits _ { – 1 } ^ 1 { \frac { { d x } } { { \sqrt { 1 – { x ^ 2 } } } } } = 0 . $$

از طرفی:

$$ \large { \int \limits _ { – 1 } ^ 1 { \frac { {d x } } { { \sqrt { 1 – { x ^ 2 } } } } } } = { \left . { \left ( { \arcsin x } \right ) } \right | _ { – 1 } ^ 1 } = { \arcsin 1 – \arcsin \left ( { – 1 } \right ) } \\ \large = { \frac { \pi } { 2 } – \left ( { – \frac { \pi } { 2 } } \right ) } = { \pi . } $$

در نتیجه $$c_0=0$$.

به طور مشابه، ضرایب $$c_n$$ را محاسبه می‌‌کنیم.

بسط $$ {x^3}= \sum\limits_{n = 0}^\infty {{c_n}{T_n}\left( x \right)}$$ را در $$ {\large\frac{{{T_m}\left( x \right)}}{{\sqrt {1 – {x^2}} }}\normalsize}, m = 1,2,3, \ldots $$ ضرب می‌‌کنیم و روی بازه $$-1$$ تا $$1$$ از آن انتگرال می‌‌گیریم:

$$ \large { { \int \limits _ { – 1 } ^ 1 { \frac { { { x ^ 3 }{ T _ m } \left ( x \right ) } } { { \sqrt { 1 – { x ^ 2 } } } } d x } }
= { \int \limits _ { – 1 } ^ 1 { \left ( { \sum \limits _ { n – 0 } ^ \infty { { c _ n } { T _ n } \left ( x \right ) } } \right ) \frac { { { T _ m } \left ( x \right ) } } { { \sqrt { 1 – { x ^ 2 } } } } d x } , \; \; } } \\ \large \Rightarrow
{ { \int \limits _ { – 1 } ^ 1 { \frac { { { x ^ 3 } { T _ m } \left ( x \right ) } } { { \sqrt { 1 – { x ^ 2 } } } } d x } } }
= { { \sum \limits _ { n = 0 } ^ \infty { \left [ { { c_ n } \int \limits _ { – 1 } ^ 1 { \frac { { { T _ n } \left ( x \right ){ T _ m } \left ( x \right ) } } { { \sqrt { 1 – { x ^ 2 } } } } d x } } \right ] } , \; \; } } \\ \large \Rightarrow
{ \int \limits _ { – 1 } ^ 1 { \frac { { { x ^ 3 } { T _ m } \left ( x \right ) } } { { \sqrt { 1 – { x ^ 2 } } } } d x } } = { \frac { \pi } { 2 } { c _ m } . } $$

در اینجا از خاصیت تعامد استفاده کرده‌‌ایم.

جملات صریح $${{T_m}\left( x \right)}$$ را جایگذاری کرده و از تغییر متغیر استفاده می‌‌کنیم:

$$ \large { x = \cos t , \; \; } \Rightarrow { \arccos x = t , \; \; } \Rightarrow { - \frac { { d x } } { { \sqrt { 1 – { x ^ 2 } } } } = d t . } $$

بنابراین، حدود انتگرال‌‌گیری به صورت زیر خواهد بود:

در نتیجه:

$$ \large { { c _ m } = \frac { 2 } { \pi } \int \limits _ { – 1 } ^ 1 { \frac { { { x ^ 3 } { T _ m } \left ( x \right ) } } { { \sqrt { 1 – { x ^ 2 } } } } d x } }
= { \frac { 2 } { \pi } \int \limits _ 0 ^ 1 { { { \cos } ^ 3 } t \cos m t d t } } \\ \large
= { \frac { 2 } { \pi } \int \limits _ 0 ^ \pi { \frac { 1 } { 4 } \left ( { 3 \cos t + \cos 3 t } \right ) \cos m t d t } } \\ \large
= { \frac { 3 } { { 2 \pi } } \int \limits _ 0 ^ \pi { \cos t \cos m t d t } } + { \frac { 1 } { { 2 \pi } } \int \limits _ 0 ^ \pi { \cos 3 t \cos m t d t } . } $$

انتگرال‌‌های به دست آمده را جداگانه محاسبه می‌‌کنیم:

$$ \large { \int \limits _ 0 ^ \pi { \cos t \cos m t d t } \text { = } } \kern0pt
{ \frac { 1 } { 2 } \int \limits _ 0 ^ \pi { \left [ { \cos \left ( { t – m t } \right ) + \cos \left ( { t + m t } \right ) } \right ] d t } } \\ \large
= { \frac { 1 } { 2 } \Big [ { \left . { \Big ( { \frac { { \sin \left ( { m – 1 } \right ) t } } { { m – 1 } } } } \right . } } + { { \left . { { \frac { { \sin \left ( { m + 1 } \right ) t } } { { m + 1 } } } \Big ) } \right | _ 0 ^ \pi } \Big ] } = { 0,\;\;} \kern-0.3pt
{\text{if} \; \; m \ne 1 . } $$

برای حالت $$m=1$$:

$$ \large { \int \limits _ 0 ^ \pi { { { \cos } ^ 2 } t d t } }
= { \frac { 1 } { 2 } \int \limits _ 0 ^ \pi { \left ( { 1 + \cos 2 t } \right ) d t } }
= { \frac { 1 } { 2 } \left [ { \left . { \left ( { t + \frac { { \sin 2 t } } { 2 } } \right ) } \right | _ 0 ^ \pi } \right ] }
= { \frac { \pi } { 2 } . } $$

انتگرال دوم نیز به طور مشابه حل می‌‌شود:

$$ \large { \int \limits _ 0 ^ \pi { \cos 3 t \cos m t d t } } = { 0 , } \; \; { \text {if} \; \; m \ne 3 . } $$

برای حالت $$m=3$$، داریم:

$$ \large { \int \limits _ 0 ^ \pi { { { \cos } ^ 2 } 3 t d t } } = { \frac { 1 } { 2 } \int \limits _ 0 ^ \pi { \left ( { 1 + \cos 6 t } \right ) d t } } = { \frac { 1 } { 2 } \left [ { \left . { \left ( { t + \frac { { \sin 6 t } } { 6 } } \right ) } \right | _ 0 ^ \pi } \right ] } = { \frac { \pi } { 2 } . } $$

همانطور که می‌‌بینیم، مجموعه توابع $$1,\cos t,\cos 2t,\cos 3t, \ldots ,\cos mt, \ldots $$ روی بازه $$\left[ {0,\pi } \right]$$ متعامدند. اکنون می‌‌توان ضرایب $$c_m$$ را به دست آورد:

$$ \large { c _ m } =
\begin {cases}
0 , & m \ne 1 , 3 \\
\frac { 3 } { 4} , & m = 1 \\
\frac { 1 } { 4 } , & m = 3
\end {cases} . $$

بنابراین، بسط سری فوریه-چبیشف تابع $$f\left( x \right) = {x^3}$$ روی بازه $$\left[ { – 1,1} \right]$$ به این صورت خواهد بود:

$$ \large { f \left ( x \right ) = { x ^ 3 } } = { \frac { 3 } { 4} { T _ 1 } \left ( x \right ) + \frac { 1 } { 4 } { T _ 3 } \left ( x \right ) . } $$

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• سری فوریه مختلط — به زبان ساده
• تبدیل فوریه (Fourier Transform) — به زبان ساده
• همگرایی سری فوریه — از صفر تا صد

^^