پتانسیل مغناطیسی — به زبان ساده
در آموزشهای قبلی مجله فرادرس درباره پتانسیل الکتریکی و روابط پواسون و لاپلاس صحبت کردیم. در این آموزش قصد داریم «پتانسیل مغناطیسی» (Magnetic Potential) را بررسی کنیم. بر خلاف پتانسیل الکتریکی که نوعی پتانسیل اسکالر محسوب میشود، پتانسیل مغناطیسی در عمل یک کمیت برداری است. اگرچه پتانسیل مغناطیسی اسکالر نیز وجود دارد، اما این پتانسیل در حل مسائل مغناطیس ساکن کاربرد چندانی ندارد.
قوانین بنیادی مغناطیس ساکن در فضای آزاد
برای مطالعه مغناطیس ساکن (میدانهای یکنواخت مغناطیسی) در فضای آزاد، فقط نیاز است که بردار چگالی شار مغناطیسی ($$B$$) را بدانیم. دو قانون بنیادی مغناطیس ساکن به تعریف دیورژانس و کرل چگالی شار مغناطیسی $$B$$ میپردازند. این دو معادله در فضای آزاد به صورت زیر هستند:
$$\nabla . B = 0$$
معادله (۱)
$$\nabla \times B = \mu_0 J$$
معادله (۲)
طبق قضیه هلمهولتز با دانستن دیورژانس و کرل یک بردار، میتوان آن را به طور کامل تعیین کرد.
$$\mu_0$$ در این روابط، نفوذپذیری مغناطیسی فضای آزاد است و به صورت زیر تعریف میشود:
$$\mu_0 = 4 \pi \times 10^{-7} (H/m)$$
پتانسیل مغناطیسی برداری
همانطور که در مبحث قضیه هلمهولتز گفتیم، چگالی شار مغناطیسی یا $$B$$ یک بردار بدون دیورژانس است. یعنی:
$$\nabla .B = 0$$
معادله (۳)
یعنی $$B$$، سلونوئیدی است. در نتیجه $$B$$ را میتوان به صورت کرل یک میدان برداری دیگر ($$A$$) نوشت. بنابراین خواهیم داشت:
$$B = \nabla \times A$$
معادله (۴)
میدان برداری $$A$$ را «پتانسیل مغناطیسی برداری» (Vector Magnetic Potential) مینامند. واحد SI این بردار، وبر بر متر (Wb/m) است. بنابراین اگر پتانسیل مغناطیسی برداری ($$A$$) برای یک توزیع جریان پیدا شود، میتوان چگالی شار مغناطیسی ($$B$$) را از طریق اعمال اپراتور کرل روی بردار $$A$$ یافت. این عمل همانند پتانسیل الکتریکی $$V$$ و میدان الکتریکی ($$E$$) بدون کرل در الکتریسیته ساکن است. رابطه میدان الکتریکی و پتانسیل الکتریکی به صورت زیر است:
$$E = -\nabla V$$
طبق قضیه هلمهولتز برای تعریف کامل یک بردار، به دیورژانس و کرل آن نیاز است. بنابراین، معادله (۴) به تنهایی برای تعریف $$A$$ کافی نیست و لازم است دیورژانس پتانسیل مغناطیسی نیز مشخص شود. اگر از دو طرف معادله (۴) کرل بگیریم، با توجه به معادله (۲) خواهیم داشت:
$$ \nabla \times \nabla \times A = \mu_0 J$$
معادله (۵)
کِرل کرل یک بردار به صورت زیر نوشته میشود:
$$\nabla \times \nabla \times A = \nabla(\nabla. A)- \nabla^2 A\\
\nabla^2 A = \nabla(\nabla.A)-\nabla\times\nabla\times A
$$
این رابطه، تعریف $$\nabla^2 A$$ یا لاپلاسین $$A$$ است. در مختصات کارتزین داریم:
$$\nabla^2 A = a_x \nabla^2 A_x + a_y\nabla^2 A_y + a_z \nabla^2 A_z.
$$
بنابراین برای مختصات کارتزین، لاپلاسین میدان برداری $$A$$ یک میدان برداری است و مولفههای آن، لاپلاسین (دیورژانسِ گرادیان) مولفه مشابه در میدان برداری $$A$$ است. هرچند، این موضوع برای دستگاههای مختصاتی استوانهای و کروی صحیح نیست. برای مختصات استوانهای لاپلاسین بردار $$A$$ به صورت زیر تعریف میشود:
$$\nabla^2 A = \left( \nabla^2 A_r-\frac{2}{r^2} \frac{\partial A_\phi}{\partial \theta } - \frac {A_r}{r^2}\right) \hat r + \left( \nabla^2 A_\phi +\frac{2}{r^2}\frac{\partial A_r}{\partial \phi} - \frac{A_\phi}{r^2} \right) \hat \phi + (\nabla^2 A_z)\hat z$$
برای مشاهده لاپلاسین بردار $$A$$ در مختصات کروی، میتوانید به تقلب نامه الکترومغناطیس مراجعه کنید.
حال اگر رابطه (۵) را بازنویسی کنیم، خواهیم داشت:
$$\nabla (\nabla . A)- \nabla^2 A = \mu_0 J$$
معادله (6)
با هدف ساده کردن معادله (۶)، رابطه زیر را فرض میکنیم:
$$\nabla . A = 0$$
معادله (۷)
با این فرض، میتوان معادله (۶) را به صورت زیر بازنویسی کرد:
$$\nabla ^2 A = - \mu_0 J$$
معادله (۸)
معادله (۸) به نام «معادله پواسون برداری» (Vector Poisson's Equation) شناخته میشود. در مختصات کارتزین، معادله (۸) با سه معادله پواسون اسکالر زیر همارز است:
$$\nabla ^2 A_x = - \mu_0 J_x ,\\
\nabla ^2 A_y = - \mu_0 J_y , \\
\nabla ^2 A_z = - \mu_0 J_z . $$
معادله (۹)
همانطور که در مطلب حل مسائل الکتریسیته ساکن دیدیم، معادله پواسون در فضای آزاد به صورت زیر نوشته میشود:
$$\nabla ^2 V= -\frac{\rho}{\varepsilon_0}$$
معادله (10)
حل خاص معادله (10) به صورت زیر است:
$$V= \frac{1}{4 \pi \varepsilon_0} \int_{V'}\frac{\rho}{R}dv'$$
معادله (۱۱)
بنابراین جواب معادله (۹) برای پتانسیل برداری در جهت $$x$$ به صورت زیر خواهد بود:
$$A_x= \frac{\mu_0}{4 \pi}\int_{V'}\frac{J_x}{R}dv'$$
معادله (۱۲)
همین حل، برای پتانسیلهای برداری در جهتهای $$y$$ و $$z$$ نیز معتبر است. با جمع همه این مولفهها، خواهیم داشت:
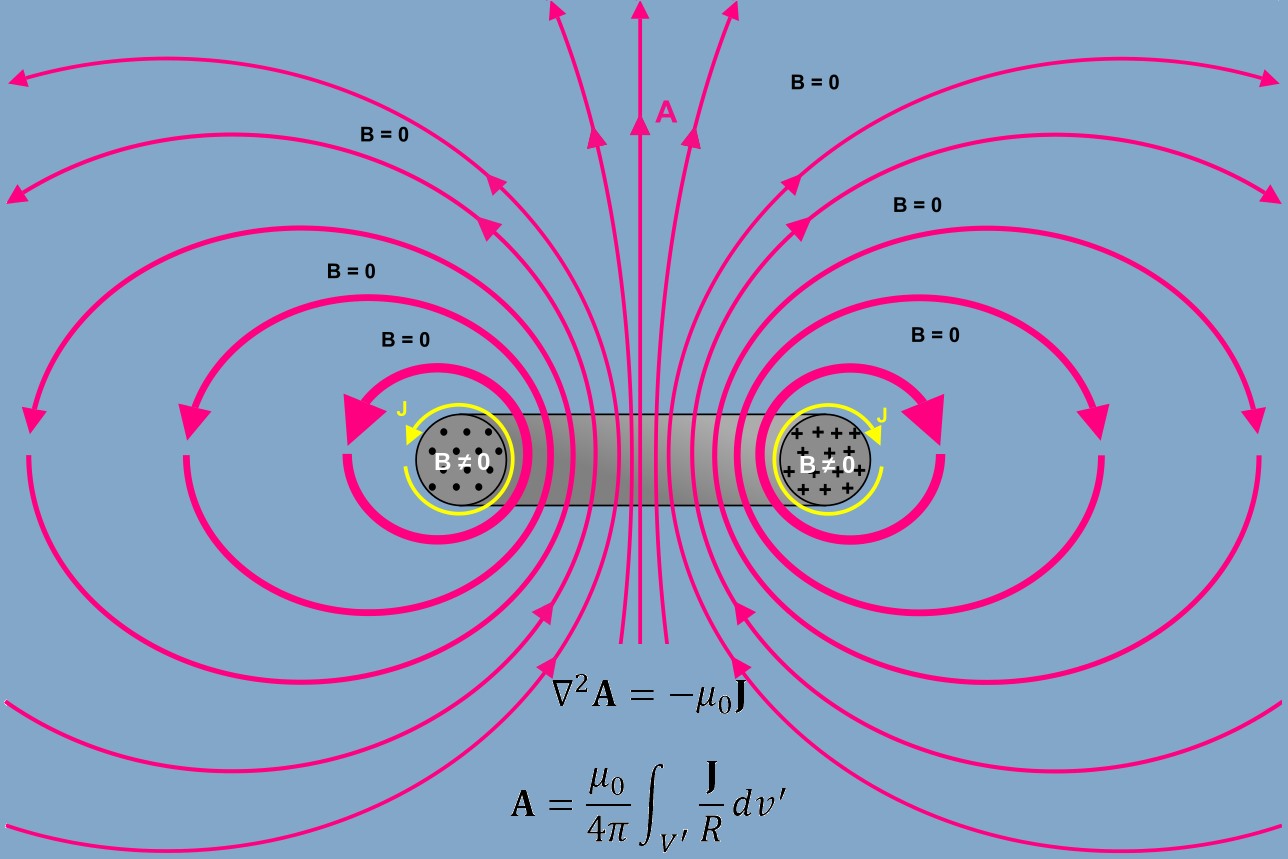
$$A = \frac{\mu_0}{4 \pi}\int_{V'}\frac{J}{R}dv' \, \, \, \, \, \, (Wb/m)$$
معادله (۱۳)
معادله (۱۳) بیان میکند که میتوان پتانسیل مغناطیسی برداری $$A$$ را بر حسب چگالی جریان $$J$$ محاسبه کرد. چگالی شار مغناطیسی $$B$$ نیز با استفاده از رابطه $$\nabla \times A$$ قابل محاسبه است. رابطه پتانسیل برداری $$A$$ و شار مغناطیسی $$\Phi$$ به صورت زیر است:
$$\Phi = \int_s B.ds$$
معادله (۱۴)
واحد شار مغناطیسی در سیستم SI، وبر (Wb) است. طبق قضیه استوکس داریم:
$$\Phi =\int_S (\nabla \times A).ds= \oint_C A.dl \, \, \, \, \, (Wb)
$$
معادله (15)
در این معادله $$S$$، سطح در بر دارنده منحنی $$C$$ است.
بنابراین پتانسیل برداری $$A$$ اهمیت فیزیکی دارد و انتگرال خطی آن در هر مسیر بسته با کل شار مغناطیسی گذرنده از سطح محصور شده توسط این مسیر برابر است.
پتانسیل مغناطیسی اسکالر
معادله (۲) را در نظر بگیرید. در یک ناحیه بدون جریان ($$J=0$$) داریم:
$$\nabla \times B = 0$$
معادله (16)
همانطور که مشاهده میشود، چگالی شار مغناطیسی $$B$$ فاقد کرل است و میتوان آن را به صورت گرادیان یک میدان اسکالر نوشت. رابطه زیر را در نظر بگیرید:
$$B= -\mu_0 \nabla V_m$$
معادله (17)
$$V_m$$ در معادله (۱۷)، «پتانسیل مغناطیسی اسکالر» (Scalar Magnetic Potential) نام دارد و واحد آن آمپر است. علامت منفی در معادله (17) قراردادی است. به این ترتیب پتانسیل مغناطیسی، دوگان پتانسیل الکتریکی ($$V$$) خواهد شد. نفوذپذیری مغناطیسی $$\mu_0$$ نیز یک عدد ثابت است. بنابراین میتوان اختلاف پتانسیل مغناطیسی بین دو نقطه $$P_1$$ و $$P_2$$ را مطابق رابطه زیر تعریف کرد:
$$V_{m2}-V_{m1} = -\int_{P_1}^{P_2}\frac{1}{\mu_0}B.dl$$
معادله (18)
اگر بار مغناطیسی با چگالی حجمی $$\rho_m$$ در حجم $$V'$$ وجود داشته باشد، میتوان $$V_m$$ را به صورت زیر نوشت:
$$V_m =\int_{V'} \frac{1}{4 \pi}\frac{\rho_m}{R}dv'$$
معادله (19)
پس از محاسبه پتانسیل مغناطیسی اسکالر، چگالی شار مغناطیسی $$B$$ با استفاده از معادله (17) قابل محاسبه است.
بارهای مغناطیسی مجزا هرگز در طبیعت یا آزمایشگاه مشاهده نشده است. بنابراین بارهای مغناطیسی، مصنوعی فرض میشوند. به هر روی، در نظر گرفتن این مدل ریاضی و غیر فیزیکی از بارهای مغناطیسی موهومی برای تشریح روابط مغناطیس ساکن و ایجاد یک رابطه دوگانی میان پتانسیل الکتریکی و پتانسیل مغناطیسی و توضیح جریانهای گردشی میکروسکوپی به عنوان منابع مغناطیس، الزامی است.
میدان مغناطیسی برای یک آهنربای میلهای با میدان مغناطیسی یک «دوقطبی مغناطیسی» (Magnetic Dipole) یکسان است. به صورت قراردادی فرض میشود که قطبهای شمال و جنوب یک آهنربای الکتریکی میلهای به ترتیب محل بارهای مغناطیسی مثبت و منفی را نشان میدهد. فرض میشود که بارهای مغناطیسی موهومی $$+q_m$$ و $$-q_m$$ در آهنربای میلهای با فاصله $$d$$ از هم جدا شدهاند. به این ترتیب، یک «دوقطبی مغناطیسی معادل» (Equivalent Magnetic Dipole) خواهیم داشت. ممان این دوقطبی مغناطیسی به صورت زیر تعریف میشود:
$$m = q_m d = a_n IS.$$
معادله (20)
پتانسیل مغناطیسی اسکالر $$V_m$$ ایجاد شده به وسیله این دوقطبی مغناطیسی، به صورت زیر قابل محاسبه است:
$$V_m = \frac{m. a_R}{4 \pi R^2}$$
معادله (۲۱)
با جایگزین کردن معادله (۲۱) در معادله (۱۷) میتوان چگالی شار مغناطیسی را یافت.
ذکر این نکته ضروری است که پتانسیل مغناطیسی اسکالر $$V_m$$ در معادله (۲۱) برای یک دوقطبی مغناطیسی با دوگان این مسئله یعنی دوقطبی الکتریکی قابل مقایسه است. پتانسیل الکتریکی یک دوقطبی الکتریکی به صورت زیر است:
$$V= \frac{p.a_R}{4 \pi \varepsilon R^2}$$
معادله (۲۲)
همانطور که گفتیم، پتانسیل مغناطیسی اسکالر با این فرض تعریف شد که چگالی شار مغناطیسی $$B$$ فاقد کرل باشد. یعنی پتانسیل مغناطیسی اسکالر $$V_m$$ فقط برای نقاط بدون جریان صحیح است.
در ناحیهای که جریان وجود دارد، میدان مغناطیسی «غیر پایستار» (Non-Conservative) خواهد بود و پتانسیل مغناطیسی اسکالر تابعی با یک مقدار نخواهد بود. بنابراین اختلاف پتانسیل مغناطیسی تعریف شده در معادله (۱۸)، به مسیر انتگرالگیری وابسته میشود. به همین دلایل، در مطالعه میدانهای مغناطیسی در مواد مغناطیسی، از روش جریان گردشی و پتانسیل مغناطیسی برداری مرتبط با آن ($$A$$) بیشتر از بار مغناطیسی موهومی و پتانسیل مغناطیسی اسکالر مرتبط با آن ($$V_m$$) استفاده میشود. خواص ماکروسکوپی یک آهنربای میلهای به وسیله جریانهای گردشی میکروسکوپی (جریان آمپری) در اتمهای ماده توضیح داده میشود. این جریانها به دلیل اسپین الکترونها ایجاد شدهاند.
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:









