نیمه عمر و محاسبات آن — به زبان ساده

در این مقاله قصد داریم تا با زبانی ساده به مبحث نیمه عمر و نحوه محاسبه آن بپردازیم. به طور خلاصه، منظور از نیمه عمر یک ماده، مدت زمانی است که مقدار آن به نصف کاهش پیدا میکند. در ابتدا از عبارت نیمه عمر تنها برای رادیو ایزوتوپهایی نظیر «اورانیوم» (Uranium) یا «پلوتونیوم» (Plutonium) استفاده میکردند که در اثر پرتوزایی، مقدارشان به نصف میرسید.
در حال حاضر عبارت نیمه عمر نه تنها در فیزیک هستهای برای مواد رادیواکتیو، بلکه برای هر مادهای که طی مدت زمانی خاص، مقدار آن با پیروی از تابعی خاص به نصف مقدار اولیهاش میرسد، استفاده میشود. برای آشنایی با محاسبه نیمه عمر، در ادامه این مقاله همراه ما باشید.
مفهوم نیمه عمر
برای محاسبه نیمه عمر، نیاز به یک مدلسازی ریاضی داریم. برای این امر، تابع نمایی نزولی گزینهای مناسب است. بدین جهت تابع زیر را در نظر بگیرید.
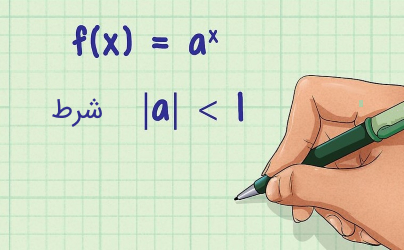
برای تابع فوق، با افزایش $$x$$، مشاهده میشود که $$f(x)$$ به سمت صفر میل میکند. در نتیجه تابعی ایدهآل جهت مدلسازی ریاضی برای پدیده فیزیکی مد نظر است. دقت داشته باشید که هدف ما محاسبه مدت زمانی است که حین گذر آن، مقدار ماده به نصف مقدار اولیه خود میرسد. برای اینکه تابع ریاضی بیشتر مفهوم فیزیکی به خود بگیرد، مولفه $$t$$ را که بیانگر زمان است، جایگزین پارامتر ریاضی $$x$$ میکنیم.
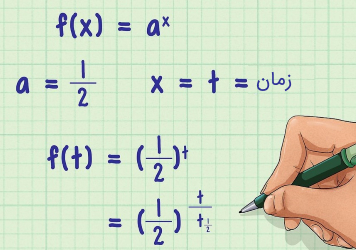
اگر برایتان سوال است که چرا مقدار $$a$$ را $$\frac{1}{2}$$ انتخاب کردهایم، لطفاً تا انتهای مطلب صبر کنید. دقت شود که در اینجا مولفه $$t$$ تنها نمایانگر گذر زمان است و نیمه عمر را مشخص نمیکند. قدم بعدی این است که مولفه $$t_{\frac{1}{2}}$$ به معنی نیمه عمر را به توان تابع ریاضی وارد کنیم. دقت شود که تابع $$f(t)$$، بیانگر مقدار ماده با واحد جرم است. پس برای بدون بُعد کردن توان در عبارت ریاضی (حذف بُعد زمانی) باید مولفه $$t$$ با مفهوم گذر زمان را بر $$t_{\frac{1}{2}}$$ (نیمه عمر) تقسیم کنیم که در شکل فوق قابل مشاهده است. قدم بعدی اضافه کردن مولفهای است که واحد آن از جنس جرم باشد.
گفتیم که $$f(t)$$ بیانگر مقدار ماده است، جهت اینکه رابطه ریاضی، مفهوم فیزیکی بیشتری به خود گیرد، میتوانیم مقدار ماده (تعداد ذرات) را با $$N(t)$$ نشان داده و آن را ضریبی از مقدار اولیه بنویسیم. در واقع مقدار اولیه با ضرب شدن در تابع نمایی نزولی از مقدارش کاسته میشود. در نتیجه:

حال برای تنها کردن مولفه $$t_{\frac{1}{2}}$$، در واقع به دست آوردن رابطهای جهت محاسبه نیمه عمر، از لگاریتم استفاده میکنیم. با گرفتن لگاریتم در مبنای $$\frac{1}{2}$$ از طرفین رابطه داریم:
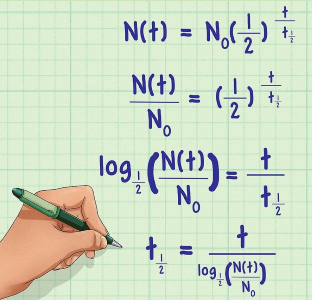
در نتیجه رابطه نیمه عمر برای مادهای به جرم اولیه $$N_{0}$$ که پس از گذشت $$t$$ ثانیه مقدار $$N(t)$$ از آن باقی مانده است، به صورت زیر محاسبه میشود:
$$\large t_{\frac{1}{2}}=\frac{t}{\log_\frac{1}{2}(\frac{N(t)}{N_{0}})}$$
$$\large N(t)=N_{0}(\frac{1}{2})^{\frac{t}{t_{\frac{1}{2}}}}$$
جهت جمعبندی، پارامترهای رابطه فوق به شرح زیر هستند:
- $$t_{\frac{1}{2}}$$ : نیمه عمر، مدت زمانی که طول میکشد ماده به نصف مقدار اولیه خودش برسد.
- $$t$$ : مدت زمان سپری شده
- $$N(t)$$ : مقدار ماده پس از گذشت $$t$$ ثانیه
- $$N_{0}$$ : مقدار اولیه ماده در زمان $$t=0$$
از رابطه فوق دلیل انتخاب $$\frac{1}{2}$$ که در ابتدای مقاله مطرح کردیم، مشخص است. در واقع اگر مدت زمان سپری شده برابر با نیمه عمر شود، مقدار $$N(t)$$ به نصف مقدار اولیه خود یعنی $$\frac{N_{0}}{2}$$ میرسد. در فیزیک هستهای معمولا به $$N_{0}$$ هستههای مادر اولیه میگویند. ممکن است که به جز رابطه فوق، دو رابطه زیر را نیز برای محاسبه نیمه عمر دیده باشید:
$$\large N(t)=N_{0}e^{-t/\tau }$$
$$\large N(t)=N_{0}e^{-\lambda t}$$
هر ۳ عبارت، جهت محاسبه نیمه عمر صحیح بوده و در واقع یک چیز هستند. λ یا $$\tau$$ درجه نزولی بودن تابع نمایی را مشخص میکنند. به عبارت زیر دقت کنید:
$$\large t_{1/2}={\frac{\ln(2)}{\lambda}}=\tau\ln(2)$$
مثال ۱
300 گرم از مادهای رادیواکتیو در اختیار داریم که با گذشت 180 ثانیه، مقدارش به 112 گرم کاهش مییابد. نیمه عمر این ماده چقدر است؟
$$\large t_{\frac{1}{2}}=\frac{t}{\log_\frac{1}{2}(\frac{N(t)}{N_{0}})} \Rightarrow t_{\frac{1}{2}}=\frac{180s}{\log_\frac{1}{2}(\frac{112gr}{300gr})}=127s$$
مثال ۲
یک راکتور هستهای، 20 کیلوگرم اورانیوم ۲۳۲ تولید میکند. اگر نیمه عمر اورانیوم 70 سال باشد، پس از چه مدت، مقدار اورانیوم تولید شده به 0.1 کیلوگرم میرسد؟
$$\large t_{\frac{1}{2}}=\frac{t}{\log_\frac{1}{2}(\frac{N(t)}{N_{0}})}$$
$$\Rightarrow t=t_{\frac{1}{2}}\times{\log_\frac{1}{2}(\frac{N(t)}{N_{0}})}=70years\times{\log_\frac{1}{2}(\frac{0.1kg}{20kg})}=535years$$
در صورتیکه این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشود:
- مجموعه آموزشهای فیزیک
- آموزش مبانی فیزیک ذرات بنیادی (Particle physics)
- مجموعه آموزشهای دروس شیمی
- تفاوت بین شکافت و همجوشی هستهای چیست؟
- رآکتور هستهای چیست؟ — به زبان ساده
- معادله شرودینگر -- به زبان ساده
^^










