نقطه عطف تابع — به زبان ساده

پیش‌تر در وبلاگ فرادرس مفاهیم مربوط به تابع توضیح داده شد. هم‌چنین در مطلبی جداگانه، نحوه بدست آوردن ماکزیمم و مینیمم تابع را توضیح دادیم. همان‌طور که در این مطالب نیز توضیح داده شد، ماکزیمم یا مینیمم تابع در محلی رخ می‌دهد که مشتق اول آن برابر با صفر باشد. شاید این سوال در ذهن شما شکل گرفته باشد، که مشتق دوم یک تابع نشان دهنده چه مفهومی است؟ با استفاده از مشتق دوم می‌توان نقطه عطف تابع را یافت. در این مطلب قصد داریم تا این مفهوم را شرح دهیم.

مفهوم نقطه عطف تابع

تابعی همچون $$ \large y = f \left ( x \right ) $$ را به صورتی در نظر بگیرید که در نقطه $$ \large x _ 0 $$ پیوسته است.

فیلم آموزش حسابان ۲ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

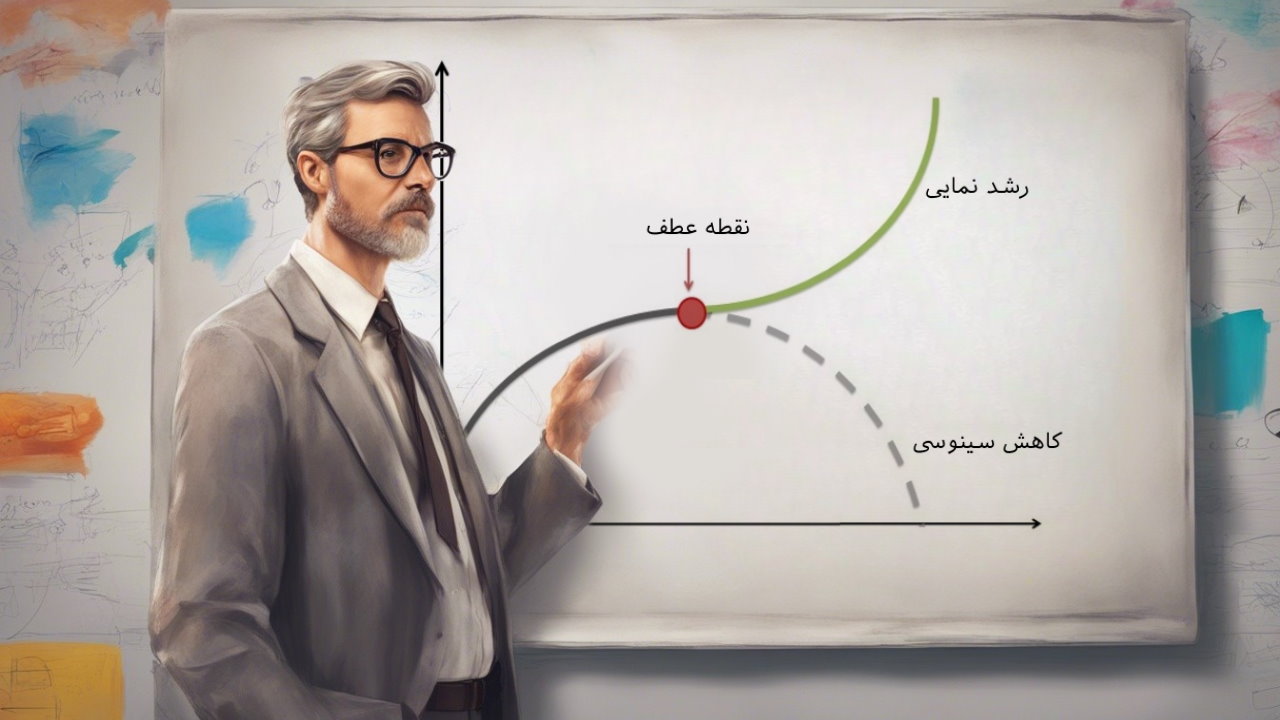
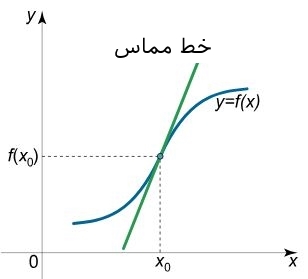
این تابع می‌تواند دارای مشتقِ $$ \large f ^ \prime ( x _ 0 ) $$ بینهایت یا محدودی در نقطه $$ \large x _ 0 $$ نیز باشد. اگر با گذشت تابع از نقطه $$ \large x _ 0 $$ جهت تقعر تابع عوض شود، در این صورت نقطه مذکور، نقطه عطف نامیده می‌شود. در شکل زیر نمونه‌ای از تغییر خمیدگی در یک تابع فرضی نشان داده شده است.

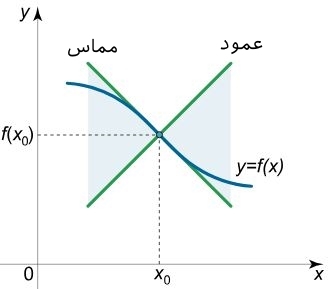
نکته جالب در مورد نقطه عطف این است که خطوط عمود و مماس بر منحنی تابع در این نقطه به یکدیگر عمود هستند. در شکل زیر این دو خط برای یک تابع فرضی ترسیم شده است.

شرط لازم برای یک نقطه عطف

اگر $$ x _ 0 $$ نقطه عطف تابع $$ f ( x ) $$ باشد و این تابع در نقطه $$ x _ 0 $$ مشتق‌پذیر باشد، در این صورت مشتق دوم تابع در این نقطه برابر با صفر خواهد بود. بنابراین می‌توان گفت در نقطه عطف، رابطه زیر برقرار است.

$$ \large f ^ { \prime \prime } \left ( { { x _ 0 } } \right ) = 0 $$

فیلم آموزش ریاضی ۳ – پایه دوازدهم علوم تجربی در فرادرس

کلیک کنید

به منظور اثبات گزاره فوق، فرض کنید مشتق تابع $$ f $$ در نقطه $$ x _ 0 $$ غیر صفر باشد ($$ \large f ^ { \prime \prime } \left ( { { x _ 0 } } \right ) \ne 0 $$). در این صورت بازه‌ای همچون $$ \large δ $$ اطراف $$ \large x _ 0 $$ وجود دارد که در آن تابع $$ \large f ( x ) $$ علامتش را حفظ می‌کند. بنابراین در قالب ریاضیات، گزاره‌ زیر را می‌توان بیان کرد:

$$ \large { f ^ { \prime \prime } \left ( { { x _ 0 } } \right ) \lt 0 \; \; \text{or}\;\;\;}\kern-0.3pt { f^ { \prime \prime } \left ( { { x _ 0 } } \right ) \lt 0 \;\forall \;x \in \left ( { { x _ 0 } – \delta , { x _ 0 } + \delta } \right) } $$

عبارت فوق نشان می‌دهد که در بازه $$ ( x _ 0 − δ , x _0 + δ ) $$ تقعر تابع مطلقا پایین ($$ f ^ {\prime\prime} (x) < 0 $$) یا به سمت بالا ($$ f ^ {\prime\prime} (x) > 0 $$) است. بنابراین نقطه مذکور، نقطه عطف نخواهد بود. بنابراین فرض غیر صفر بودن مشتق دوم اشتباه است.

شرط کافی اول برای نقطه عطف

اگر تابع $$ \large f ( x ) $$ در نقطه $$ \large x _ 0 $$ دارای مشتق بوده و مشتق دوم تابع در بازه $$ \large \delta $$ اطراف نقطه $$ \large x _ 0 $$ تغییر علامت بدهد، در این صورت نقطه $$ \large x _ 0 $$، نقطه عطف محسوب می‌شود.

شرط کافی دوم برای نقطه عطف

فرض کنید مشتق دوم یک تابع در نقطه‌ای برابر با صفر باشد ($$ \large f ^ { \prime \prime } \left ( { { x _ 0 } } \right ) = 0 $$). در این صورت اگر مشتق سوم $$ \large f ^ { \prime \prime \prime } \left ( { { x _ 0 } } \right ) \ne 0 $$ غیر صفر باشد، $$ \large x _ 0 $$، نقطه عطف خواهد بود.

مثال ۱

نقاط عطف تابع زیر را بیابید.

$$ \large { f \left ( x \right ) \text { = }}\kern0pt { { x ^ 4 } – 12 { x ^ 3 } + 48 { x ^ 2 } + 12 x + 1 } $$

در ابتدا مشتق اول و دوم تابع را به صورت زیر بدست می‌آوریم.

$$ \large \begin {align*} { f ^ { \prime } \left ( x \right ) }
& = { { \left( { { x ^ 4 } – 12 { x ^ 3 } + 48 { x ^ 2 } + 12 x + 1 } \right ) ^ \prime } }
\\ & = { 4 { x ^ 3 } – 36 { x ^ 2 } + 96 x + 12 }
\\ & = { 4 \left ( { { x ^ 3 } – 9 { x ^ 2 } + 24 x + 3 } \right ) } \end {align*} $$

$$ \large \begin {align*} { f ^ { \prime \prime } \left ( x \right ) }
& = { { \left ( { 4 \left ( { { x ^ 3 } – 9 { x ^ 2 } + 24 x + 3 } \right ) } \right ) ^ \prime } }
\\ & = { 4 \left ( { 3 { x ^ 2 } – 18 x + 24 } \right ) }
\\ & = { 12 \left ( { { x ^ 2 } – 6 x + 8 } \right ) } \end {align*} $$

بنابراین ریشه‌های مشتق دوم برابرند با:

$$ \large \begin {align*} { f ^ { \prime \prime } \left ( x \right ) = 0 \;\;} & \Rightarrow
{ 12 \left ( { { x ^ 2 } – 6 x + 8 } \right ) = 0 \; \; } \\ & \Rightarrow
{ { x ^ 2 } – 6x + 8 = 0 \;\;} \\ & \Rightarrow
{{x_1} = 2,\; { x _ 2 } = 4 } \end {align*} $$

حال می‌توان از شرط کافی دوم به صورت زیر استفاده کرد. بدین منظور مشتق سوم را محاسبه می‌کنیم.

$$ \large \begin {align*} { f ^ { \prime \prime \prime } \left ( x \right ) }
& = { { \left ( { 12 \left ( { { x ^ 2 } – 6 x + 8 } \right ) } \right ) ^ \prime } }
\\ & = { 12 \left ( { 2 x – 6 } \right ) = 24 \left ( { x – 3 } \right ) } \end {align*} $$

با قرار دادن نقاط $$ \large \begin {align*} { x _ 1 } = 2 \end {align*} $$ و $$ \large \begin {align*} { x _ 1 } = ۴ \end {align*} $$ در رابطه بالا می‌بینید که مشتق سوم در این نقاط غیر صفر است. بنابراین هر دوی این نقاط، نقطه عطف هستند.

مثال 2

نقاط عطف تابع $$ \large \begin {align*} f \left ( x \right ) = { x ^ 2 } \ln x \end {align*} $$ را بیابید.

فیلم آموزش ریاضیات گسسته در فرادرس

کلیک کنید

مشتقات اول و دوم تابع برابرند با:

$$ \large \begin {align*} f ^ { \prime } \left ( x \right ) & = { \left ( { { x ^ 2 } \ln x } \right ) ^ \prime }
\\ & = { { \left( {{x^2}} \right)^\prime }\ln x + { x ^ 2 } { \left ( { \ln x } \right ) ^ \prime } }
\\ & = { 2 x \ln x + { x ^ 2 } \cdot \frac { 1 } { x } }
\\ & = { 2 x \ln x + x = x \left ( { 2 \ln x + 1 } \right ) } \end {align*} $$

$$ \large \begin {align*} f ^ { \prime \prime } \left ( x \right ) & = { \left[ { x \left ( { 2 \ln x + 1 } \right ) } \right ] ^ \prime }
\\ & = { x ^ { \prime } \left( {2\ln x + 1} \right) + x { \left ( { 2 \ln x + 1 } \right)^\prime } }
\\ & = { 2 \ln x + 1 + x \cdot \frac { 2 } { x } = 2 \ln x + 3 } \end {align*} $$

بنابراین ریشه‌های مشتق دوم برابرند با:

$$ \large \begin {align*} { \Rightarrow 2 \ln x + 3 \;\;} \Rightarrow
{ \ln x = – \frac { 3 } { 2 } \; \; } \Rightarrow
{ x = { e ^ { – \large \frac { 3 } { 2 } \normalsize} } = \frac { 1 } { { \sqrt { { e ^ 3 } } } } } \end {align*} $$

مثال ۳

نقاط عطف تابع $$ \large \begin {align*} f \left ( x \right ) = { e ^ { \sin x } } \end {align*} $$ را بیابید.

فیلم آموزش ریاضی عمومی ۲ در فرادرس

کلیک کنید

مشتق اول و دوم برابرند با:

$$ \large \begin {align*} f ^ { \prime } \left ( x \right ) & = { \left ( { { e ^ { \sin x } } } \right ) ^ \prime }
\\ & = { { e ^ { \sin x } } { \left ( { \sin x } \right ) ^ \prime } }
\\ & = { { e ^ { \sin x } } \cos x } \end {align*} $$

$$ \large \begin {align*} f ^ { \prime \prime } \left ( x \right ) & = {\left( {{e^{\sin x}}\cos x} \right ) ^ \prime }
\\ & = { { \left ( { { e ^ { \sin x } } } \right ) ^ \prime } \cos x + { e ^ { \sin x } } { \left ( { \cos x } \right ) ^ \prime } }
\\ & = { { e ^ { \sin x } } { \cos ^ 2 } x – { e ^ { \sin x } } \sin x }
\\ & = { { e ^ { \sin x } } \left ( { { { \cos } ^ 2 } x – \sin x } \right) } \end {align*} $$

به منظور پیدا ریشه‌های مشتق دوم از تغییر متغیر $$ \large \begin {align*} t = \sin ( x ) \end {align*} $$ استفاده می‌کنیم. با استفاده از این تغییر متغیر، معادله فوق به صورت زیر قابل حل خواهد بود.

$$ \large \begin {align*} t = \frac{{ – 1 + \sqrt 5 } } { 2 } & = \frac { { \sqrt 5 – 1 } } { 2 } \; \;
\\ & \Rightarrow
{ \sin x = t = \frac { { \sqrt 5 – 1 } } { 2 } \; \; } \\ & \Rightarrow
{ { x _ n } = { \left ( { – 1} \right ) ^ n } \arcsin \frac { { \sqrt 5 – 1 } } { 2 } \; \; } , & \kern-0.3pt{n \in Z } \end {align*} $$

بنابراین بینهایت نقطه می‌توان یافت که مشتق آن‌ها برابر با صفر است. اما در بازه $$ \large \begin {align*} \left[ { 0,2 \pi } \right] \end {align*} $$ تنها دو نقطه زیر هستند که مشتق دوم به ازای آن‌ها برابر با صفر است.

$$ \large \begin {align*} { x _ 1 } = \arcsin \frac { { \sqrt 5 – 1 } } { 2 } \approx 0,66 \ \ \ , \ \;\;\; \kern-0.3pt
& { { x _ 2 } = \pi – \arcsin \frac { { \sqrt 5 – 1}}{2} }\approx {2,48 } \end {align*} $$

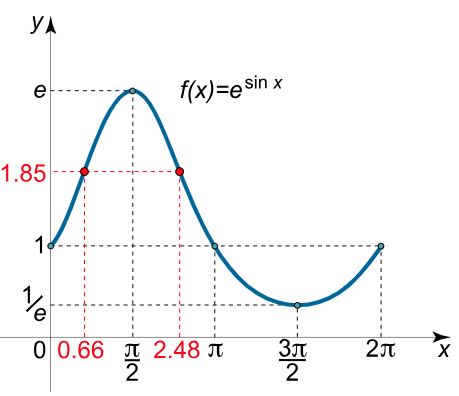
نمودار شکل زیر نقاط بدست آمده و تابع $$ \large \begin {align*} f \end {align*} $$ را نشان می‌دهند. همان‌طور که در بالا نیز بدست آمد، مشتق دوم تابع به صورت زیر است.

$$ \large \begin {align*} {f^{\prime\prime}\left( x \right) }
= {{e^{\sin x}}\left( {{{\cos }^2}x – \sin x} \right) }
= {{e^{\sin x}}\left( { – {\sin^2}x – \sin x + 1} \right)} \end {align*} $$

تابع فوق به ازای عبور از دو ریشه $$ \large \begin {align*} x _ 1 , x _ 2 \end {align*} $$ تغییر علامت می‌دهند. بنابراین هر دوی آن‌ها را می‌توان به عنوان نقاط عطف در نظر گرفت.