نامساوی برنولی (Bernoulli’s Inequality) — به زبان ساده

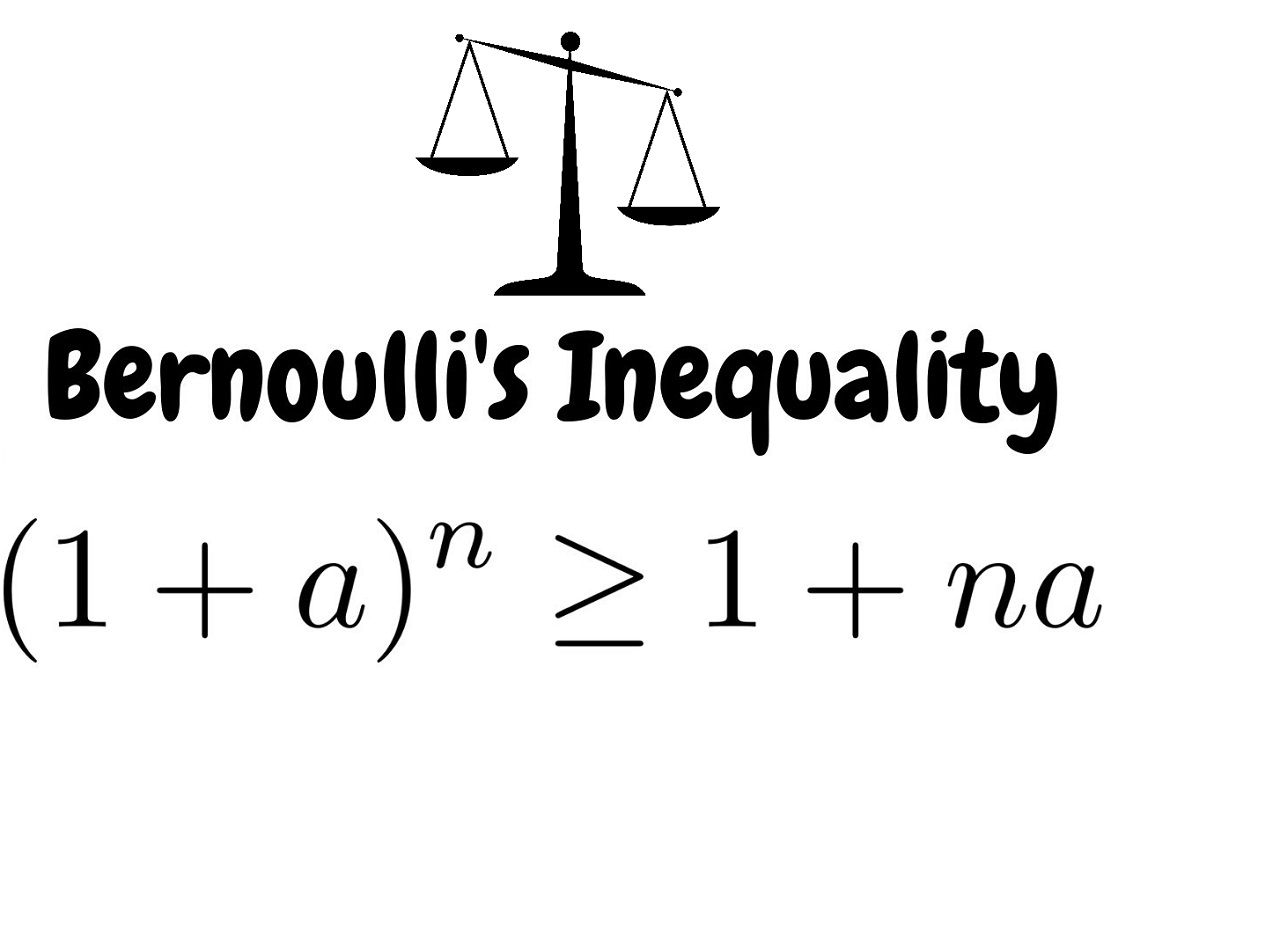
یکی از نامساوی‌های پرکاربرد در «آنالیز حقیقی» (Real Analysis)، «نامساوی برنولی» (Bernoulli's Inequality) است. اسم این نامساوی برگرفته از نام «ژاکوب برنولی» (Jacob Bernoulli) است که به بررسی این نامساوی در رساله خود در سال 1689 پرداخت. هدف او در بررسی این نامساوی، پیدا کردن کران پایین برای توان‌های مختلفی از $$1+x$$ بود.

برای آشنایی با دیگر نامساوی‌های ریاضی می‌توانید مطلب نامساوی های ریاضی — به زبان ساده را مطالعه کنید. همچنین خواندن نوشتارهای فضای متریک و نامساوی مثلثی — به زبان ساده و نامساوی شوارتز — به زبان ساده نیز خالی از لطف نیست. البته اگر می‌خواهید با نامساوی‌ها و نامعادله‌ها آشنا شوید بهتر است مطالب رسم نامعادلات و نامساوی‌ های خطی — به زبان ساده و معادله و نامعادله در ریاضی — پیدایش و کاربردها را نیز مطالعه کنید.

نامساوی برنولی

بسیاری از نامساوی‌های مطرح در ریاضیات برمبنای نامساوی برنولی اثبات یا نوشته شده‌اند. برنولی سعی داشت به کمک یک رابطه ریاضی، کران بالایی برای معادله ساده بسازد. او ابتدا رابطه $$1+x$$ را در نظر گرفت و برای توان‌های صحیح از این عبارت، به یک نامساوی یا نابرابری دست یافت.

فیلم آموزش تئوری احتمالات در فرادرس

کلیک کنید

به این ترتیب، فرم کلی نامساوی برنولی برحسب توان‌های $$1+x$$ نوشته شده است. در این حالت طبق نامساوی برنولی یک کران پایین برای این توان‌ها می‌توان در نظر گرفت که به صورت زیر خواهد بود.

$$\large {\displaystyle (1+x)^{r}\geq 1+rx}$$

در اینجا $$r$$ عدد صحیح و $$r\geq 0$$ است و $$x \geq -2$$ است. در ادامه متن علت اینکه باید $$x$$ بزرگتر از $$-2$$ باشد را مشخص خواهیم کرد. البته اگر $$r$$ زوج باشد، این نامساوی را برای همه اعداد حقیقی نیز می‌توان در نظر گرفت. برای آنکه بهتر رابطه بین $$1+x$$ و توان‌های مشخص شود را درک کنید، لازم است که به تصویر زیر توجه داشته باشید. در اینجا $$r=3$$ در نظر گرفته شده است. منحنی قرمز رنگ تابع $$y=(1+x)^3$$ را نشان داده و $$۳x+1$$ نیز با رنگ آبی دیده می‌شود.

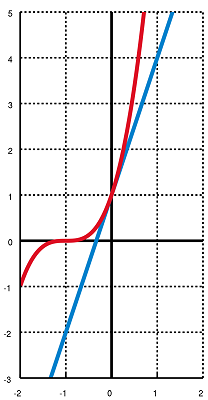
این نمودار نشان می‌دهد که همیشه نمودار قرمز رنگ در بالای نمودار آبی رنگ قرار دارد. در نتیجه می‌توان منحنی $$1+3x$$ را کران پایین برای تابع $$(x+1)^3$$ در نظر گرفت. این طور به نظر می‌رسد که این تابع در بعضی فاصله‌ها «محدب» (Convex) و در بعضی دیگر «مقعر» (Concave) است. این نامساوی را برای اعداد حقیقی $$x\geq -1$$ و $$x\neq0$$ می‌توان به صورت نامساوی اکید نیز نوشت، به شرطی که $$r\geq2$$ باشد.

$$\large{\displaystyle (1+x)^{r}>1+rx}$$

رابطه ۱

اغلب از نامساوی برنولی برای اثبات نامساوی‌های دیگر استفاده می‌شود. در نتیجه می‌توان این نامساوی را به عنوان پایه و اساس نامساوی‌های دیگر در نظر گرفت، هرچند که کمتر مورد توجه قرار گرفته است.

اثبات نامساوی برنولی

اثبات نامساوی برنولی به روش‌های مختلفی امکان‌پذیر است. از آنجایی که این نامساوی در اثبات نامساوی‌های دیگر به کار گرفته می‌شود، می‌تواند کاربرد زیادی داشته باشد. در ادامه به بررسی پنج شیوه‌ مختلف برای اثبات نامساوی برنولی خواهیم پرداخت.

۱. اثبات نامساوی برنولی به کمک استقراء

برای اثبات نامساوی برنولی در رابطه ۱، می‌توان از استقرا استفاده کرد. از آنجایی که اولین مقدار برای $$r$$ در نامساوی برنولی صفر است، نقطه اول استقرا را از این مقدار آغاز می‌کنیم. فرض بر این است که $$r \in \{0,1\}$$ است سپس برای $$r+2$$ نیز نامساوی را اثبات می‌کنیم.

نکته: چون مقدار حداقل برای $$r$$ صفر در نظر گرفته شده، میزان افزایش را $$2$$‌ در نظر گرفته‌ایم.

برای $$r=0$$، نامساوی برقرار است:

$$\large{\displaystyle (1+x)^{0}=1\geq 1+0x = 1}$$

برای $$r=1$$ خواهیم داشت:

$$\large{\displaystyle (1+x)^{r}=1+x\geq 1+x=1+rx}$$

فیلم آموزش حل معادلات دیفرانسیل با متمتیکا Mathematica در فرادرس

کلیک کنید

حال فرض می‌کنیم که نامساوی برای $$r=k$$ برقرار است. یعنی داریم،

$$\large{\displaystyle (1+x)^{k}\geq 1+kx}$$

حالا با در نظر گرفتن $$k=r+2$$ می‌توان نوشت:

$$\large{\displaystyle {\begin{aligned}(1+x)^{k+2}&=(1+x)^{k}(1+x)^{2} \\&\geq (1+kx)\left(1+2x+x^{2}\right)\\&=1+2x+x^{2}+kx+2kx^{2}+kx^{3}\\&=1+(k+2)x+kx^{2}(x+2)+x^{2}\\&\geq 1+(k+2)x\end{aligned}}}$$

در سطر دوم از اتحاد مربع کامل و فرض استقرا کمک گرفته‌ایم. پس از ضرب و ساده‌ کردن جمله‌ها، برای رسیدن به سطر آخر اثبات، با توجه به مثبت بودن $$x^2$$ و $$x+2$$ که از پیش‌فرض‌های نامساوی برنولی محسوب می‌شوند، این جملات را حذف کرده‌ایم. در نتیجه سمت راست نامساوی باز هم کوچکتر می‌شود.

۲. اثبات نامساوی برنولی به کمک مشتق‌گیری

به کمک مشتق‌گیری از تابع $$f(x)=(1+x)^r–rx–1$$ نیز می‌توان این نامساوی را به سادگی اثبات کرد. برای مشاهده اثبات به روش مشتق به نوشتار نامساوی های ریاضی — به زبان ساده مراجعه کنید. مشتق این تابع برابر است با:

$$ \large { f’ \left ( x \right ) = { \left [ { { { \left ( { 1 + x } \right ) } ^ r } – r( x – 1) } \right ] ^ \prime } } = { \alpha \left [ { { { \left ( { 1 + x } \right ) } ^ {r – 1 } } – 1 } \right ] . } $$

با استفاده از تعیین علامت این مشتق و شرط $$r>0$$ و عدد صحیح بودن آن، به نامساوی برنولی خواهیم رسید.

۳. اثبات نامساوی برنولی به کمک میانگین هندسی و حسابی

یک روش ساده برای اثبات نامساوی برنولی در حالتی که $$0\leq r \leq 1$$ و $$x \geq -1$$ است، استفاده از میانگین حسابی (Artihmetic Mean) و هندسی (Geometric Mean) است.

فرض کنید دو مقدار $$\lambda_1$$ و $$\lambda_2$$، حقیقی و نامنفی هستند. به این ترتیب میانگین حسابی وزنی ( $$AM_w$$) و میانگین هندسی وزنی ($$GM_w$$) برای دو مقدار $$1$$ و $$1+x$$ به صورت زیر نوشته می‌شوند.

$$\large AM_w=\dfrac{\lambda_1\cdot 1+\lambda_2\cdot (1+x)}{\lambda_1+\lambda_2}$$

$$\large GM_w= \sqrt[\lambda_1+\lambda_2\;\;]{1^{\lambda_1}(1+x)^{\lambda_2}}=\sqrt[\lambda_1+\lambda_2\;\;]{(1+x)^{\lambda_2}}$$

از آنجایی که میانگین حسابی از میانگین هندسی بزرگتر است، خواهیم داشت:

$$\large \dfrac{\lambda_1\cdot 1+\lambda_2\cdot (1+x)}{\lambda_1+\lambda_2}\ge \sqrt[\lambda_1+\lambda_2\;\;]{(1+x)^{\lambda_2}}$$

توجه داشته باشید که

$$\large \dfrac{\lambda_1\cdot 1+\lambda_2\cdot (1+x)}{\lambda_1+\lambda_2}=\dfrac{\lambda_1+\lambda_2+\lambda_2x}{\lambda_1+\lambda_2}=1+\dfrac{\lambda_2}{\lambda_1+\lambda_2}x$$

و همچنین

$$\large \sqrt[\lambda_1+\lambda_2\;\;]{(1+x)^{\lambda_2}}=(1+x)^{\frac{\lambda_2}{\lambda_1+\lambda_2}}$$

در نتیجه خواهیم داشت:

$$\large1+\dfrac{\lambda_2}{\lambda_1+\lambda_2}x\ge (1+x)^{\frac{\lambda_2}{\lambda_1+\lambda_2}}$$

رابطه۲

با جایگزین کردن  $$=\dfrac{\lambda_2}{\lambda_1+\lambda_2}$$ در رابطه ۲ به نتیجه دلخواه خواهیم رسید که به شکل زیر است.

$$\large 1+rx\ge (1+x)^r$$

البته توجه دارید که $$0\leq \dfrac{\lambda_2}{\lambda_1+\lambda_2}\leq 1$$ پس شرط $$ {\displaystyle 0\leq r\leq 1}$$ نیز محقق شده است.

۴. اثبات با استفاده از دنباله هندسی

می‌دانیم که نامساوی برنولی را می‌توان به صورت دیگری نیز نوشت بطوری که همه پارامترها و متغیرها در یک طرف نامساوی قرار گیرند.

$$\large {\displaystyle (1+x)^{r}-1-rx\geq 0}$$

رابطه ۳

اگر با یک تغییر متغیر به صورت $$y=1+x$$ عمل کنیم، با استفاده از دنباله هندسی (Geometric Series) خواهیم داشت:

$$\large {\displaystyle (1+x)^{r}-1=y^{r}-1=\left(\sum _{k=0}^{r-1}y^{k}\right)\cdot (y-1)=\left(\sum _{k=0}^{r-1}(1+x)^{k}\right)\cdot x}$$

رابطه ۴

حال اگر $$x\geq 0$$ باشد، با توجه به یکنوایی توابع نمایی، برای هر یک از جملات جمع داریم $${\displaystyle (1+x)^{k}-1\geq 0}$$، پس مجموع این جملات نیز نامنفی خواهد بود. در نتیجه رابطه ۳ و به تبع آن، نامساوی برنولی اثبات می‌شود.

همچنین اگر $$0 \geq x \geq -2$$ باشد، داریم $$ {\displaystyle 1\geq (1+x)^{k}}$$ و به این ترتیب همه جملات جمع، یعنی $$ {\displaystyle (1+x)^{k}-1}$$ در رابطه ۴ نیز منفی یا صفر هستند، در نتیجه مجموع نیز منفی خواهد بود. از آنجایی که حاصلضرب دو عدد منفی، مثبت خواهد شد، حاصل ضرب $$x$$ و $$ \sum _{k=0}^{r-1}\left((1+x)^{k}-1\right)$$ نیز مثبت شده و نامساوی رابطه ۴، محقق خواهد شد.

۵. اثبات به کمک قضیه دوجمله‌ای

روش دیگر برای اثبات نامساوی برنولی، استفاده از قضیه دو جمله‌ای است. همانطور که در دیگر مطالب فرادرس خوانده‌اید، قضیه بسط دو جمله‌ای به صورت زیر نوشته می‌شود:

$$\large {\displaystyle (1+x)^{r}=1+rx+{\tbinom {r}{2}}x^{2}+...+{\tbinom {r}{r}}x^{r}}$$

رابطه ۵

اگر فرض کنیم که $$x>0$$ است، می‌توانیم نامساوی زیر را برای بسط دو جمله‌ای بنویسیم:

$$\large {\displaystyle {\tbinom {r}{2}}x^{2}+...+{\tbinom {r}{r}}x^{r}\geq 0}$$

در نتیجه نامساوی برنولی با حذف عبارت بالا از رابطه ۵ حاصل خواهد شد. یعنی داریم:

$$\large {\displaystyle (1+x)^{r}\geq 1+rx}$$

همچنین اگر $$x=0$$‌ باشد، به طور وضوح نامساوی برنولی به صورت تساوی در خواهد آمد:

$$\large {\displaystyle (1+x)^{r}=1+rx}$$

اگر $$-1\leq x<0$$ باشد، تغییر متغیر $$y=-x$$ را در نظر گرفته و براساس اینکه $$0 <x\leq1$$ کافی است با جایگزین کردن $$x$$ با $$-y$$ در رابطه ۵، بسط دوجمله‌ای را بنویسیم.

$$\large {\displaystyle (1-y)^{r}=1-ry+{\tbinom {r}{2}}y^{2}+...+(-1)^{r}{\tbinom {r}{r}}y^{r}}$$

نکته: براساس قضیه بسط دو جمله‌ای داریم:

$$\large {\displaystyle 1=r+{\tbinom {r}{2}}+...+(-1)^{r}{\tbinom {r}{r}}}$$

در نتیجه

$$\large{\displaystyle r-1={\tbinom {r}{2}}+...+(-1)^{r}{\tbinom {r}{r}}}$$

رابطه ۶

همچنین برای مقادیر $$0 <y\leq 1$$ می‌دانیم که $$ {\displaystyle y^{2}\geq y^{3}\geq ...\geq y^{r}}$$.

از این نکته استفاده می‌کنیم و هر یک از $$y^r$$ را در جمله متناسب خود در رابطه ۶ ضرب می‌کنیم. واضح است که این حاصل‌ضرب‌ها از مقدار خود جمله در هر بخش از رابطه ۶ کوچکتر هستند، در نتیجه حاصل جمع این جملات نیز از سمت راست رابطه ۶ کوچکتر خواهند بود.

$$\large {\displaystyle (1-y)^{r}=1-ry+{\tbinom {r}{2}}y^{2}+...+(-1)^{r}{\tbinom {r}{r}}y^{r}\geq 1-ry}$$

با جایگزینی $$y$$ با $$-x$$ به نامساوی برنولی خواهیم رسید.

$$\large {\displaystyle (1+x)^{r}\geq 1+rx}$$

نکته: توجه کنید که اثبات بوسیله بسط دوجمله‌ای فقط برای حالتی که $$r$$ عدد مثبت و صحیح باشد، مناسب است.

نامساوی برنولی تعمیم یافته

همانطور که اشاره شد، اثبات‌ها برای نامساوی برنولی در اغلب موارد براساس مقدار صحیح و حتی نامنفی برای $$r$$ نوشته شده‌اند. در حالتی که این نامساوی برحسب هر عدد حقیقی $$r$$ نوشته شود، وضعیت متفاوت بوده و بهتر است از شیوه اثبات به کمک مشتق استفاده کنیم. نامساوی برنولی را در حالت تعمیم یافته، می‌توان به صورت زیر بیان کرد. به این ترتیب مقدار $$r$$ از اعداد حقیقی گرفته خواهد شد.

فیلم آموزش مبانی آنالیز عددی – بخش دوم در فرادرس

کلیک کنید

اگر $$x >-1$$ آنگاه به ازاء $$r \leq 0$$ یا $$r \geq 1$$ خواهیم داشت:

$$\large{\displaystyle (1+x)^{r}\geq 1+rx}$$

و به ازاء $$0 \leq r \leq 1$$ داریم:

$$\large{\displaystyle (1+x)^{r}\leq 1+rx}$$

در صورتی که $$x\neq 0 $$ و $$r\neq 0 , 1$$ آنگاه نامساوی‌های بالا به صورت نامساوی اکید در خواهند آمد.

همانطور که دیده شد، در نامساوی برنولی یا نسخه تعمیم یافته آن، یک کران پایین برای $$(1+x)^r$$ ارائه می‌شود. ولی برای پیدا کردن کران بالا از نامساوی زیر استفاده می‌شود.

$$\large {\displaystyle (1+x)^{r}\leq e^{rx}}$$

رابطه 8

که در آن $$r>0$$ است. همانطور که می‌دانید منظور از $$e$$‌، عدد نپر (Napierian  Number) است. این عدد متعلق به مجموعه اعداد موهومی (گنگ) بوده و مقدار تقریبی آن نیز $$e=2.71...$$ است.

اثبات نامساوی رابطه 8 به کمک نامساوی زیر صورت می‌گیرد.

$$\large {\displaystyle (1 + \dfrac{1}{k})^k < e}$$

فرم‌های دیگر از نامساوی برنولی

فرض کنید که $$t\geq1$$ و $$0\leq x\leq 1$$ باشد، آنگاه

$$\large (1-x)^{t}\geq 1-xt$$

با فرض تعلق $$t$$ به مجموعه اعداد صحیح، اثبات این نامساوی به کمک سری هندسی امکان‌پذیر است. کافی است که $$y=1-x$$ را در نظر بگیرید، در نتیجه

$$\large t=1+1+\dots +1\geq 1+y+y^{2}+\ldots +y^{{t-1}}={\frac {1-y^{t}}{1-y}}$$

طرف راست نامساوی بالا به این علت نوشته شده که اگر مقداری در بازه صفر تا یک قرار داشته باشد، توان‌های نامنفی از آن همیشه از خود مقدار کوچکتر است. یعنی

$$\large 0\leq y \leq 1 \rightarrow y^r \leq y, r\;\; \text{are integers}$$

در نتیجه به سادگی خواهیم داشت:

$$\large xt\geq 1-(1-x)^{t}$$

کاربردهای نامساوی برنولی

نامساوی برنولی در اثبات نامساوی‌های دیگر به کار گرفته می‌شود. در نتیجه این نامساوی در بین نامساوی‌های پایه‌ قرار می‌گیرد. در ادامه به چند مورد از کاربردهای نامساوی برنولی در اثبات نامساوی‌های دیگر می‌پردازیم.

فیلم آموزش آنالیز عددی پیشرفته در فرادرس

کلیک کنید

نامساوی جنسن (Jensen Inequality)

یکی از روش‌های اثبات نامساوی جنسن، استفاده از نامساوی برنولی است. برای مشاهده نحوه به کارگیری این نامساوی در اثبات نامساوی جنسن به نوشتار نامساوی جنسن (Jensen Inequality) — به زبان ساده مراجعه کنید.

نامساوی میانگین هندسی و حسابی

در قسمت‌های قبلی این نوشتار مشاهده کردید که به کمک نامساوی بین میانگین هندسی و حسابی، می‌توان نامساوی برنولی را اثبات کرد. خوشبختانه عکس این عمل نیز امکان‌پذیر است. یعنی با فرض درست بودن نامساوی برنولی می‌توان نامساوی بین میانگین هندسی و حسابی را بدست آورد. کافی است روندی که در اثبات نامساوی برنولی طی کردیم را به صورت برعکس انجام دهیم.

نامساوی مک‌لورن (Maclaurin's Inequality)

یکی دیگر از کاربردهای نامساوی برنولی البته در حالت تعمیم یافته، اثبات نامساوی مک‌لورن (Maclaurin's inequality) است. این نامساوی را می‌توان به صورت زیر بیان کرد.

اگر $$a_1,a_2,\ldots,a_n$$ مقادیر حقیقی مثبت باشند و $$S_k$$ را به صورت زیر تعریف کنیم:

$$\large S_{k}={\frac {\displaystyle \sum _{{1\leq i_{1}<\cdots <i_{k}\leq n}}a_{{i_{1}}}a_{{i_{2}}}\cdots a_{{i_{k}}}}{\displaystyle {n \choose k}}}$$

آنگاه رابطه زیر برای $$k$$های مختلف برقرار است:

$$\large S_{1}\geq {\sqrt {S_{2}}}\geq {\sqrt[ {3}]{S_{3}}}\geq \cdots \geq {\sqrt[ {n}]{S_{n}}}$$

و زمانی نامساوی به تساوی تبدیل می‌شود که همه $$a_i$$ها برابر باشند.

این نامساوی زمانی که $$n=2$$ باشد به همان نامساوی میانگین حسابی و هندسی تبدیل می‌شود. زمانی که $$n=4$$ باشد این نامساوی بهتر نمایش داده می‌شود.

$$\large {\begin{aligned}&{}\quad {\frac {a_{1}+a_{2}+a_{3}+a_{4}}{4}}\\[8pt]&{}\geq {\sqrt {{\frac {a_{1}a_{2}+a_{1}a_{3}+a_{1}a_{4}+a_{2}a_{3}+a_{2}a_{4}+a_{3}a_{4}}{6}}}}\\[8pt]&{}\geq {\sqrt[ {3}]{{\frac {a_{1}a_{2}a_{3}+a_{1}a_{2}a_{4}+a_{1}a_{3}a_{4}+a_{2}a_{3}a_{4}}{4}}}}\\[8pt]&{}\geq {\sqrt[ {4}]{a_{1}a_{2}a_{3}a_{4}}}.\end{aligned}}$$

خلاصه و جمع‌بندی

در این نوشتار با نامساوی برنولی آشنا شدیم. نحوه اثبات و کاربردهای آن در اثبات دیگر نامساوی‌های ریاضی نیز مورد بحث قرار گرفت. از این نامساوی برای اثبات رابطه بین میانگین حسابی و میانگین هندسی نیز استفاده می‌شود. نامساوی جنسن که بوسیله نامساوی برنولی صحت آن اثبات می‌شود از مهم‌ترین نامساوی‌ها در حوزه آمار و احتمال است بطوری که بسیاری از روابط بین شاخص‌های آماری از طریق این نامساوی حاصل می‌شوند.