میدان‌ برداری پایستار — به زبان ساده (+ دانلود فیلم آموزش رایگان)

در مطالب گذشته وبلاگ فرادرس مفهوم میدان برداری را توضیح دادیم. با استفاده از این توابع می‌توان معادله دیفرانسیل حاکم بر پدیده‌های فیزیکی را توصیف کرد. از طرفی برخی از این توابع، از ویژگی‌ خاصی برخوردارند. تغییرات این توابع برداریِ خاص، وابسته به مسیر نبوده و تنها به ابتدا و انتهای مسیر وابسته است. به چنین توابعی، میدان‌ برداری پایستار یا میدان برداری پایسته گفته می‌شود. از این رو در این مطلب قصد داریم تا نحوه شناسایی این میدان‌ها را توضیح داده و روش بدست آوردن میدان اسکالر مرتبط با این توابع را شرح دهیم.

میدان‌ برداری پایستار

در ابتدا فرض کنید $$\overrightarrow F $$ میدانی برداری و پیوسته روی $$D$$ باشد. در این صورت زمانی میدان $$\overrightarrow F $$ پایسته تلقی می‌شود که انتگرال آن روی خمِ فرضی $$C$$ وابسته به مسیر نباشد. در چنین مواردی می‌توان تابعی اسکالر به نام $$ f $$ را به نحوی یافت که در رابطه $$ \overrightarrow F = \nabla f $$ صدق کند. تابع $$f$$ تحت عنوان تابع پتانسیل شناخته می‌شود. یک میدان برداری پایسته دارای ویژگی‌های زیر است.

فیلم آموزش ریاضی عمومی ۲ در فرادرس

کلیک کنید

• $$ \displaystyle \int \limits _ { C } { { \overrightarrow F \small \bullet \, d \, \overrightarrow r } } $$ وابسته به مسیر نیست.
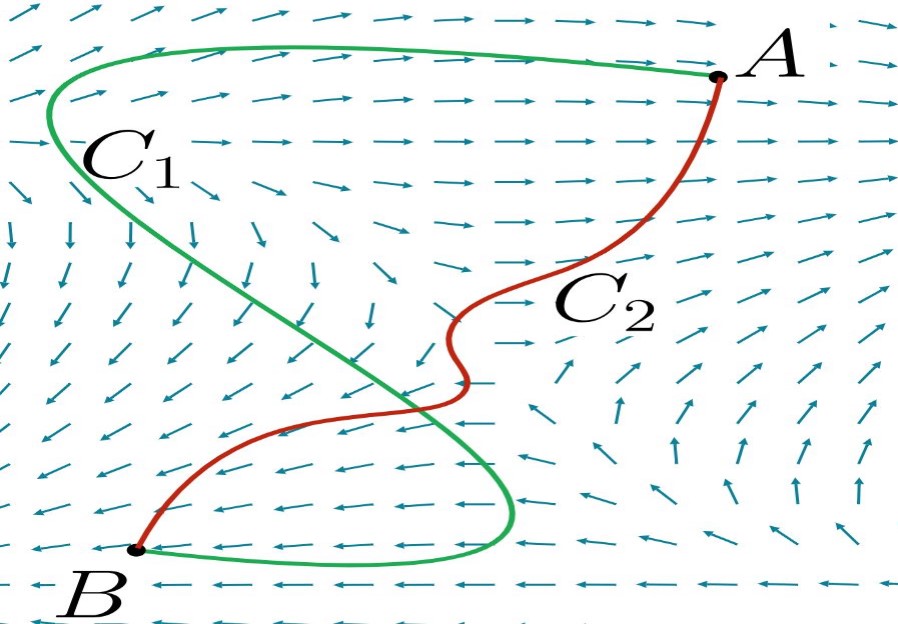
• مسیر‌های $$ C _ 1 , C _ 2 $$ را مسیر‌هایی دلخواه در نظر بگیرید که نقطه آغازین و پایانی آن‌ها یکی است. در این صورت حاصل دو انتگرال $$ \displaystyle \int \limits _ { { { C _ 1 } } } { { \overrightarrow F\small \bullet \,d\,\overrightarrow r}} = \int \limits _ { { { C_ 2 } } } { { \overrightarrow F \small \bullet \, d \, \overrightarrow r } } $$ با هم برابر است.

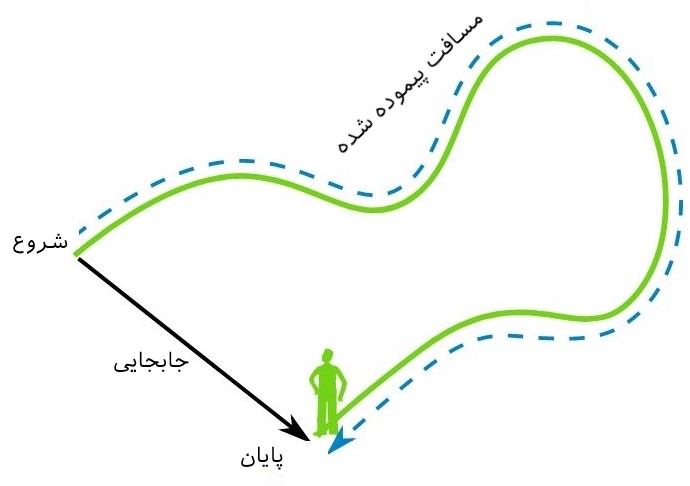
به مسیری همچون $$C$$، در صورتی مسیر بسته گفته می‌شود که نقاط ابتدایی و انتهایی آن‌ها یکی باشد. برای نمونه یک دایره مسیری بسته محسوب می‌شود. در شکل از دو مسیر مختلف، شخصی بین دو نقطه جابجا شده است. همان‌طور که در شکل نیز نشان داده شده، مسافت پیموده شده وابسته به مسیر است. این در حالی است که جابجایی تنها وابسته به نقطه ابتدا و انتهایی است که شخص در آن قرار گرفته است.

با استفاده از فرضیات فوق در ادامه در مورد تعیین پایسته بودن یک بردار و نحوه بدست آوردن تابع پتانسیل مربوط به آن صحبت خواهیم کرد.

قضیه: فرض کنید $$ \overrightarrow F = P \, \overrightarrow i + Q \, \overrightarrow j $$ میدانی برداری روی ناحیه $$D$$ باشد. در این صورت اگر رابطه بین $$P$$ و $$Q$$ به صورت زیر باشد، آن‌گاه میدان $$\overrightarrow {F}$$ پایستار در نظر گرفته می‌شود.

$$ \large \frac { { \partial P } } { { \partial y } } = \frac { { \partial Q } } { { \partial x } } $$

مثال ۱

وضعیت پایستاری یا ناپایستاری میدان‌‌های برداری زیر را بررسی کنید.

$$ (1) \ \ \ \large \overrightarrow F \left ( { x , y } \right ) = \left ( { { x ^ 2 } - y x } \right ) \overrightarrow i + \left ( { { y ^ 2 } - x y } \right ) \overrightarrow j $$

$$ (2) \ \ \ \large \overrightarrow F\left( {x,y} \right) = \left( { 2 x{{ { e} } ^ {x y }} + {x^2}y{{{e}}^{xy}}} \right)\overrightarrow i + \left ( { { x ^ 3 } { { { e } } ^ { x y }} + 2y} \right)\overrightarrow j $$

پاسخ (۱): روند حل مسئله کاملا واضح است. با تشخیص $$P$$ و $$Q$$ کافی است مشتق جزئی آن‌ها را محاسبه کنید.

$$ \large \begin{align*} P & = { x ^ 2 } - y x \ \ \Rightarrow \frac { { \partial P } } { { \partial y } } = - x \\ Q & = { y ^ 2 } - x y \ \ \Rightarrow \frac { { \partial Q } } { { \partial x } } = - y \end{align*} $$

همان‌طور که می‌بینید مشتق جزئی عبارت‌های تشکیل‌دهنده میدان برداری با هم برابر نیستند؛ بنابراین این میدان پایسته نیست.

پاسخ (۲): در مورد تابع شماره ۲ نیز مشتق جزئی اجزای آن برابر است با:

$$\large \begin{align*} P & = 2 x { { { e } } ^ { x y } } +{ x ^ 2 } y{ { {
e } } ^{ x y } }\Rightarrow \ \ \frac { { \partial P } } { { \partial y } } = 2 { x ^ 2 }{{{ e } } ^ { x y } } + { x ^2 } { { { e } } ^ { x y} } + { x^ 3 } y { { {e}}^{xy}} = 3{x^2}{{ {e
} } ^{ x y}} + { x ^ 3}y{{ { e } }^ { x y }}\\ Q & = {x^3}{{ {e}}^{xy}} + 2y \Rightarrow \ \ \frac { { \partial Q } } { { \partial x } } = 3 { x ^2}{{ { e } }^ { x y }} + {x^3}y{{ {e}}^{xy}}\end{align*}$$

همان‌طور که می‌بینید دو مشتق جزئیِ بالا با هم برابرند؛ بنابراین این میدان پایسته محسوب می‌شود. با استفاده از مثال فوق نحوه تشخیص یک میدان برداری را یاد گرفتید. حال زمان آن رسیده تا نحوه بدست آوردن تابع پتانسیل مرتبط با میدان برداری پایستار را توضیح دهیم. در ابتدا باید بگوییم که برای یک میدان برداری پایستار می‌توان تابعی اسکالر تحت عنوان، تابع پتانسیل در نظر گرفت. بدین منظور در ابتدا باید بگوییم که رابطه بین میدان و تابع پتانسیل به صورت زیر است.

$$\large \nabla f = \frac { { \partial f } } { { \partial x } } \, \overrightarrow i + \frac { { \partial f } }{ { \partial y } } \, \overrightarrow j = P \, \overrightarrow i + Q \, \overrightarrow j = \overrightarrow F $$

عبارت فوق نشان‌دهنده یک رابطه برداری است. از این رو مولفه‌های آن باید با هم برابر باشند. لذا با برابر قرار دادن مولفه‌ها داریم:

$$\large \frac { { \partial f } } { { \partial x } } = P \ , \ \frac { { \partial f } } { { \partial y } } = Q $$

برای بدست آوردن تابع $$f$$، از رابطه فوق انتگرال گرفته و خواهیم داشت:

$$\large f \left ( { x , y } \right ) = \int { { P \left ( { x , y } \right ) \, d x } } \ \ ,\ \ f \left ( { x , y } \right ) = \int { { Q \left ( { x , y } \right ) \, d y } } $$

با حل دو معادله فوق، شکل نهایی تابع $$f$$ بدست خواهد آمد. در ادامه مثالی ارائه شده که در آن نحوه بدست آوردن تابع $$f$$ شرح داده شده است.

مثال ۲

پایستار بودن یا نبودن توابع زیر را مشخص کرده و تابع پتانسیل آن‌ها را بدست آورید.

$$ \large (1) \ \ \ \overrightarrow F = \left ( { 2 { x ^ 3 } { y ^ 4 } + x } \right ) \overrightarrow i + \left ( { 2 { x ^ 4 } { y ^ 3 } + y } \right) \overrightarrow j $$

$$ \large (2) \ \ \ \overrightarrow F \left( {x,y} \right) = \left( { 2 x { { { e } } ^ { x y } } + {x^2}y{{ {e}}^{xy}}} \right)\overrightarrow i + \left( {{x^3}{{ { e } } ^ { x y}} + 2 y } \right ) \overrightarrow j $$

پاسخ (۱): همان‌طور که پیش‌تر نیز بیان شد، به منظور تعیین وضعیت پایستاری میدان، در ابتدا باید توابع $$P,Q$$ را تشخیص دهید. در ادامه این توابع و مشتقات آن‌ها ارائه شده است.

$$\large \begin {align*} P & = 2{x^3}{y^4} + x \ \ \Rightarrow \ \ \frac{{\partial P}}{{\partial y}} = 8 { x^ 3 }{ y ^ 3 } \\~\\ & Q = 2{x^4}{y^3} + y \ \ \Rightarrow \ \ \frac { { \partial Q } } { { \partial x } } = 8 { x^ 3 } { y ^ 3 } \end {align*}$$

همان‌طور که می‌بینید مشتقات $$P$$ و $$Q$$ در رابطه فوق با هم برابر هستند. از این رو این میدان برداری، پایستار بوده و دارای تابع پتانسیل خواهد بود. نهایتا تابع پتانسیل به صورت زیر قابل محاسبه است.

$$\large \frac { { \partial f } } { { \partial x } } = 2 { x ^ 3 }{ y ^ 4 } + x \ \ , \ \ \frac { { \partial f } } { { \partial y } } = 2 { x ^ 4} { y ^3} + y$$

با انتگرال‌گیری داریم:

$$\large f\left( {x,y} \right) = \int { { 2 { x ^ 3 } { y ^ 4} + x\,dx}}{ \ , } \ \ f\left ( { x , y } \right) = \int{{2 { x ^ 4 } { y ^ 3 } + y \, d y } } $$

توجه داشته باشید که انتگرال سمت چپ نسبت به $$x$$ و انتگرال سمت راست نسبت به $$y$$ گرفته شده‌اند. بنابراین سمت چپ وابسته به $$x$$ و سمت راست وابسته به $$y$$ خواهد بود. در نتیجه ثابت‌های دو انتگرال چپ و راست به ترتیب می‌توانند وابسته به $$y$$ و $$x$$ باشند. با توجه به این توضیحات حاصل انتگرال سمت چپ برابر است با:

$$ \large \begin {align*} f \left ( { x , y } \right ) & = \int{{2 { x ^ 3} { y ^ 4 } + x\, d x } } \\ & = \frac { 1 } {2 } { x^ 4 } { y ^ 4 } + \frac { 1 } {2 } { x ^ 2 } + h \left( y \right ) \end{align*}$$

توجه داشته باشید که $$h(y)$$، ثابت انتگرال محسوب می‌شود. به منظور بدست آوردن آن، می‌توان از تابع $$f$$ نسبت به $$y$$ مشتق بگیریم و آن را برابر با $$Q$$ قرار دهیم.

$$\large \frac { { \partial f }} { { \partial y } } = 2 { x ^4 } { y ^3 } + h ^ { \prime } \left ( y \right ) = 2 { x ^ 4 } { y ^ 3 } + y = Q $$

نهایتا رابطه مربوط به $$y$$ را می‌توان به صورت زیر بیان کرد:

$$ \large h ^ { \prime } \left ( y \right ) = y$$

با انتگرال‌گیری از عبارت فوق، تابع $$h(y)$$ نیز به صورت زیر بدست خواهد آمد.

$$ \large h \left ( y \right ) = \int { { h ^ { \prime } \left ( y \right ) \, d y } } = \int { { y \, d y } } = \frac { 1 } {2 } { y^ 2 } + c $$

نهایتا تابع دو متغیره $$f(x,y)$$ یا تابع پتانسیل برابر است با:

$$\large f \left ( { x , y } \right ) = \frac { 1 } { 2} { x ^ 4 } { y^ 4 } + \frac { 1 } { 2 } {x ^ 2} + \frac { 1 } {2 } { y ^ 2 } + c$$

توجه داشته باشید که همواره می‌توان با استفاده از رابطه $$\nabla f = \overrightarrow F$$ پاسخ بدست آمده را بررسی کرد. توجه داشته باشید که ازای مقادیر مختلف $$c$$ می‌توان به میدان‌های اسکالر متفاوتی دست یافت.

پاسخ (۲): برای این تابع نیز دقیقا همانند پاسخ تابع اول عمل می‌کنیم. در ابتدا مشتقات جزئی به صورت زیر بدست خواهند آمد.

$$ \large \frac { { \partial f } } { { \partial x } } = 2 x { { { e } }^ {x y }} + { x ^ 2} y { { { e } } ^ { x y } } \ \ , \ \ \frac { { \partial f } } { { \partial y } } = { x ^ 3 } {{ { e } } ^ { x y } } + 2 y $$

بنابراین انتگرال‌‌ها برابرند با:

$$ \large f \left ( { x , y } \right) = \int { { 2 x {{ { e } } ^ { x y } } + { x ^ 2 } y{ { { e } } ^{ x y } } \, d x } } \ \ , \ \ f\left( {x,y} \right) = \int{{{x^3}{{ { e } } ^{ x y }} + 2y\, d y } } $$

انتگرال سمت راست را می‌توان به روش جزء به جزء بدست آورد. توجه داشته باشید که با انتگرال‌گیری، تابع خروجی می‌تواند وابسته به $$x$$ نیز باشد. حال با انتگرال‌گیری از عبارت سمت راست داریم:

$$ \large f \left ( { x , y } \right ) = { x ^ 2 } { { { e } } ^ { x y } } + { y ^ 2 } + h \left ( x \right ) $$

حال با مشتق‌گیری از عبارت فوق نسبت به $$x$$ و برابر قرار دادن آن با $$P$$، تابع $$h(x)$$ نیز بدست خواهد آمد.

$$ \large \frac { { \partial f } } { { \partial x}} = 2x{{ { e }}^{ x y } } + { x ^ 2} y { { { e } }^ { x y } } + h ^ { \prime } \left( x \right) = 2x{{ {e } } ^ { x y } } + {x^2}y{{ { e }} ^ { x y } } = P $$

بنابراین تابع پتانسیل نیز نهایتا برابر خواهد بود با:

$$ \large f \left ( { x , y } \right ) = { x^ 2 } { { { e } } ^ { x y } } + { y ^ 2 } + c $$

تاکنون در مورد میدان‌هایی صحبت کردیم که همه آن‌ها دوبعدی بودند. این در حالی است که یک میدان برداری می‌تواند سه‌بعدی نیز باشد. اما تاکنون روشی کلی به منظور تعیین پایستار بودن میدان‌های برداری ارائه نشده است. فرض کنید میدانی برداری ارائه شده که از قبل پایستار بودن آن نیز بیان شده است. در این صورت روش یافتن تابع پتانسیل مرتبط با آن مشابه با روشی است که برای میدان دوبعدی بیان شد. در حقیقت اگر تابع اسکالر $$f$$، تابع پتانسیل میدان برداری $$ \overrightarrow {F} $$ باشد، در این صورت رابطه زیر را می‌توان بین میدان برداری و تابع پتانسیل مرتبط با آن نوشت.

$$ \large \nabla f = \frac{{\partial f}}{{\partial x}}\,\overrightarrow i + \frac{{\partial f } } { { \partial y } } \, \overrightarrow j + \frac{{\partial f } } { { \partial z } } \, \overrightarrow k = P \, \overrightarrow i + Q \, \overrightarrow j + R\,\overrightarrow k = \overrightarrow F$$

مثال ۳

تابع پتانسیل میدان برداری زیر را بدست آورید.

$$ \large \overrightarrow F = 2 x { y ^ 3 } { z ^ 4 } \, \overrightarrow i + 3 { x ^ 2 } { y ^ 2 }{ z ^ 4 } \, \overrightarrow j + 4 { x ^ 2} { y ^ 3 }{ z ^ 3 } \, \overrightarrow k $$

فیلم آموزش مکانیک تحلیلی ۱ مرور و حل مثال در فرادرس

کلیک کنید

در حالت سه‌بعدی نیز دقیقا مشابه با حالت دوبعدی عمل کرده و مشتق جزئی تابع اسکالر $$f$$ را برابر با مولفه‌های میدان $$F$$ قرار می‌دهیم.

$$\large \frac { { \partial f}}{{\partial x}} = 2 x {y ^3}{z^4} \ \ , \ \ \frac{{\partial f}}{ { \partial y } } = 3 { x ^2 } { y ^2 } { z ^ 4 } \ \ , \ \ \frac{{\partial f}}{{\partial z}} = 4 { x ^ 2 } { y ^ 3 }{ z ^ 3 } $$

با انتگرال‌گیری از عبارت سمت راست داریم:

$$ \large f \left ( { x , y , z } \right ) = \int { { 2x { y ^ 3} { z ^ 4 } \, dx}} = {x ^2 }{ y^ 3} {z ^ 4 } + g \left( { y , z } \right ) $$

توجه داشته باشید که شکل عمومی تابع وابسته به هر سه متغیر است. بنابراین با محاسبه انتگرال نسبت به $$x$$ نیز ثابت باید -در حالت عمومی- وابسته به دو متغیره دیگر در نظر گرفته شود.

$$ \large f \left ( { x , y , z } \right ) = \int { { 2x { y ^ 3} { z ^ 4 } \, dx}} = {x ^2 }{ y^ 3} {z ^ 4 } + g \left( { y , z } \right ) $$

حال می‌توان از $$f$$ نسبت به $$ y $$ مشتق گرفته و برابر با $$ Q $$ قرار داد.

$$ \large \frac { { \partial f } } { { \partial y } } = 3 { x ^2 } { y ^ 2} { z ^4 } + {g _ y } \left ( { y , z } \right) = 3 { x^2 } {y^ 2} {z ^4 } = Q $$

با حل عبارت فوق، $$g$$ به صورت زیر بدست خواهد آمد.

$$ \large { g _ y } \left( {y,z} \right) = 0\hspace{0.5in} \Rightarrow \hspace{0.5in} g \left( {y,z} \right) = h\left( z \right) $$

تا به این جا تابع پتانسیلِ $$f$$ به صورت زیر بدست آمده است.

$$ \large f \left ( { x , y , z } \right ) = { x ^ 2 }{ y ^ 3 } { z ^ 4 } + h \left ( z \right ) $$

نهایتا با مشتق‌گیری از $$f$$ نسبت به $$z$$، تابع $$h$$ نیز بدست خواهد آمد.

$$ \large \frac { { \partial f } } { { \partial z } } = 4 { x ^ 2 } { y ^ 3 } { z ^ 3 } + h ^ {\prime} \left ( z \right ) = 4 { x ^ 2 } {y ^ 3 }{ z ^ 3 } = R$$

بنابراین تابع $$h$$ برابر با عددی ثابت است.

$$ h ^ { \prime } \left ( z \right ) = 0 \hspace {0.25in} \Rightarrow \hspace {0.25in} \, \, \, h \left ( z \right ) = c $$

در نتیجه نهایتا تابع پتانسیل برای این میدان برابر خواهد بود با:

$$ \large f \left ( { x , y , z } \right ) = { x ^ 2 } {y ^ 3 } { z ^ 4 } + c $$

انرژی پتانسیل

همان‌طور که در مقدمه این مطلب نیز عنوان شد، مفهوم پایستگی یک میدان برداری کاربرد بسیاری در فیزیک، برق و مکانیک دارد. برای نمونه نیرو، کمیتی برداری در فیزیک است. از این رو ممکن است این کمیت، پایسته باشد. برای نمونه می‌توان جهت بررسی پایسته بودن از مفهوم کار انجام شده طی یک مسیر استفاده کرد. در حقیقت کار انجام شده توسط نیروی متصل به جسم برابر است با:

$$ \large W = \int_C \overrightarrow{F}. \overrightarrow { d s } $$

اگر مقدار فوق روی دو مسیرِ متفاوت، یکسان باشد، در این صورت نیروی $$F$$ پایسته در نظر گرفته می‌شود. توجه داشته باشید که نیرو‌های بنیادی موجود در طبیعت همچون گرانش یا الکتریسیته، میدان‌هایی پایستار محسوب می‌شوند. با این حال نیرویی همچون اصطکاک نیرویی ناپایستار است.

برای نیرو‌های پایستار موجود در طبیعت می‌توان کمیتی تحت عنوان پتانسیل را به صورت زیر تعریف کرد.

$$ \large F = ∇ U $$

در حقیقت رابطه فوق می‌گوید گرادیان تغییرات انرژی پتانسیل جسم نشان دهنده نیروی وارد به جسم است. از طرفی با انتگرال گیری از رابطه فوق روی یک مسیر، کار انجام شده توسط نیروی گرانش نیز بدست می‌آید. بنابراین کار انجام شده در مسیر $$A B$$ برابر است با:

$$ \large \begin {align*} W & = \int _ C F . d s \\ & =\int_ C {∇U⋅ds} = U (B) - U (A) \end{align*} $$

در مطالب آینده فیزیک و ریاضی، از کاربرد‌های میدان‌های برداری پایستار مثال‌هایی ارائه خواهیم کرد. در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی و فیزیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• تابع پتانسیل و جریان پتانسیل در سیالات — از صفر تا صد
• تقلب نامه (Cheat Sheet) معادلات دیفرانسیل
• معادلات دیفرانسیل ناهمگن — به زبان ساده
• معادلات دیفرانسیل — به زبان ساده

^^