معیار واگرایی کولبک لیبلر (Kullback Leibler)— پیاده سازی در پایتون
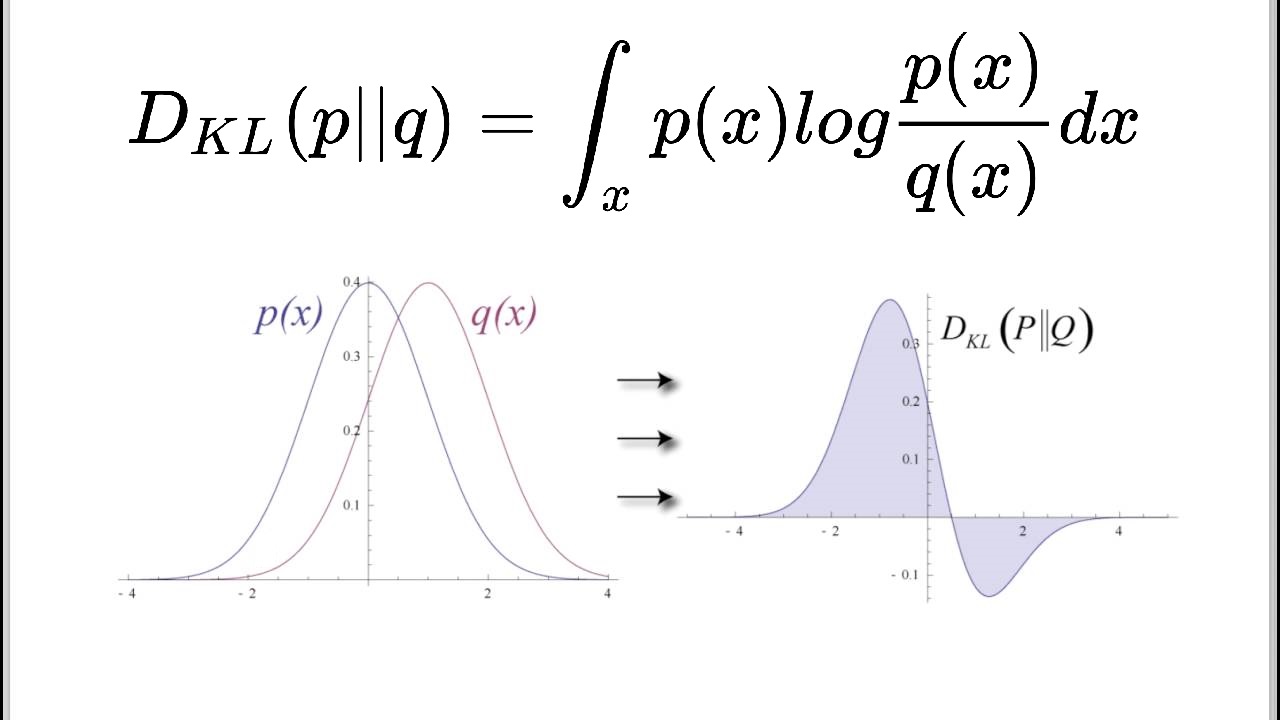
در تئوری آمار-ریاضی، معیار «واگرایی کولبک لیبلر» (Kullback-Leibler Divergence) روشی برای مشخص کردن میزان تفاوت بین دو توزیع احتمالی است. از جمله کاربردهای این معیار میتوان به سنجش تصادفی بودن در سری زمانی، بینظمی نسبی (آنتروپی شانون) در سیستمهای اطلاعاتی اشاره کرد.
به عنوان مقدمه در بحث واگرایی کولبک-لیبلر، بهتر است مطالب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال و آزمایش تصادفی، پیشامد و تابع احتمال را بخوانید. همچنین خواندن نوشتار یادگیری ماشین به زبان قضیه بیز، بی نظمی شانون و فلسفه نیز خالی از لطف نیست.
معیار واگرایی کولبک لیبلر (Kullback-Leibler Divergence)
قبل از هر چیز باید با مفاهیم اولیهای که در معیار واگرایی کولبک-لیبلر به کار میرود، آشنا شویم. تابع توزیع احتمال و متغیر تصادفی از مهمترین واژه یا مفاهیم هستند که در این نوشتار با آنها زیاد برخورد خواهیم داشت. همانطور که در مقدمه گفته شد، در دیگر نوشتارهای فرادرس این مفاهیم و اصطلاحات معرفی و در موردشان بحث شده است.
به منظور آغاز بررسی در زمینه معیار واگرایی کولبک-لیبلر به یک مثال میپردازیم. فرض کنید که شما فضانورد هستید و به فضای خارج از منظومه شمسی سفر کردهاید. در این ماموریت به کرمهای فضایی برخورد کردهاید و میخواهید این خبر هیجانانگیز را به زمین مخابره کنید. متاسفانه هزینه ارسال خبر به زمین زیاد است و شما باید پیام خود را با کمترین حجم ارسال کنید بطوری که از میزان اطلاعاتی مورد نظرتان کاسته نشود.
یک راه برای ارسال چنین اطلاعاتی رسم یک جدول یا نمودار فراوانی است که نشان میدهد با توجه به تعداد دندانها چند کرم مشاهده شده است. به این ترتیب یک توزیع احتمال برای کرمها و دندانهایشان محاسبه یا ترسیم شده است.
تابع توزیع احتمال، اطلاعات مناسبی و به صرفهتری در باره همه کرمها نسبت به ارسال اطلاعات هر یک از کرمها مخابره میکند. بعضی از این توزیعهای احتمالی دارای اسامی خاصی هستند مانند توزیع نرمال، توزیع دو جملهای و توزیع یکنواخت. برای مثال اگر بخواهیم دادههای با توزیع یکنواخت را بشناسیم کافی است فقط دو نوع اطلاعات را ارسال کنیم، مقدار پارامتر توزیع یکنواخت و تعداد کرمها.
ولی سوالی که مطرح میشود این است که از کجا متوجه شویم دادهها چه توزیعی دارند. پاسخ به این سوال توسط معیار واگرایی «کولبک-لیبلر» که به اختصار با KL نشان داده میشود میسر است. به این ترتیب میتوان میزان اختلاف بین توزیع واقعی و توزیع حدسی مورد بررسی قرار گیرد. بنابراین میتوان معیار واگرایی KL را روشی برای اندازهگیری مطابقت بین دو توزیع در نظر گرفت.
فرض کنید ۱۰۰ کرم فضایی مشاهده شده است. جدول فراوانی برحسب تعداد دندانها به صورت زیر در آمده است.
| تعداد دندان | فراوانی | درصد فراوانی (احتمال) |
| 0 | 2 | 0.02 |
| 1 | 3 | 0.03 |
| 2 | 5 | 0.05 |
| 3 | 14 | 0.14 |
| 4 | 16 | 0.16 |
| 5 | 15 | 0.15 |
| 6 | 12 | 0.12 |
| 7 | 8 | 0.08 |
| 8 | 10 | 0.1 |
| 9 | 8 | 0.08 |
| 10 | 7 | 0.07 |
نکته: جمع فراوانیها باید برابر با ۱۰۰ یعنی تعداد کرمها باشد. از طرفی میتوان نتیجه گرفت که مجموع درصد فراوانی نیز برابر با ۱ خواهد بود.
$$\large 2+3+5+14+16+15+12+8+10+8+7=100,\\ \large 0.02+0.03+0.05+0.14+0.16+0.15+0.12+0.08+0.1+0.08+0.07=1.0$$
این جدول را میتوان در نمودار زیر که به نمودار فراوانی یا هیستوگرام معروف است خلاصه کرد.
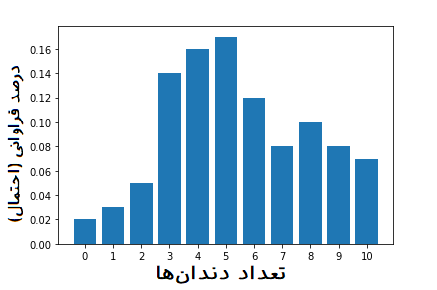
کد پایتون مربوط به تولید چنین نموداری در ادامه قابل مشاهده است. البته توجه داشته باشید که ابتدا باید کتابخانههای زیر را فراخوانی کنید.
1import matplotlib.pyplot as pylab
2import numpy as np
3from scipy.misc import factorialسپس کد زیر را اجرا کنید.
1true_data = [0.02, 0.03, 0.05, 0.14, 0.16, 0.15, 0.12, 0.08, 0.1, 0.08, 0.07]
2assert sum(true_data)==1.0
3
4pylab.bar(np.arange(len(true_data)),true_data)
5pylab.xlabel('Different Teeth Bins',fontsize=18)
6pylab.title('Probability Distribution of Space Worm Teeth',fontsize=18)
7pylab.ylabel('Probability',fontsize=18)
8pylab.xticks(np.arange(len(true_data)))
9pylab.show()مدلبندی و انتخاب توزیع مناسب
اگر ساختار و مدل احتمالی دادههای کرمهای فضایی را مشخص کنیم، به راحتی میتوانیم اطلاعات مناسب را به زمین مخابره کنیم. بنابراین احتیاج داریم که مطابقت توزیع احتمالی دادهها (جدول فراوانی) را با توزیعهایی آماری که میشناسیم اندازهگیری کنیم.
از آنجایی که مقدارهای متغیر گسسته (شمارشی) هستند، از توزیعهای گسسته به عنوان توزیعهای آزمایشی بهره میبریم. کار را ابتدا با توزیع یکنواخت (Uniform) گسسته پی میگیریم.
توزیع یکنواخت گسسته تنها یک پارامتر دارد که آن هم تعداد پیشامدها است. به این ترتیب میتوانیم رابطه زیر را بنویسیم.
$$\large p(X=x)=\dfrac{1}{11}=0.0909$$
مشخص است که پیشامدها مطابق با نمودار قبلی یا جدول فراوانی، دارای ۱۱ (از ۰ تا ۱۰) حالت مختلف است. در تصویر زیر نمودار مقایسه مطابقت توزیع یکنواخت با توزیع دادههای مربوط به دندانهای کرمهای فضایی دیده میشود.

این نمودار توسط قطعه کد زیر تولید شده است.
1def get_unif_probability(n):
2 return 1.0/n
3
4unif_data = [get_unif_probability(11) for _ in range(11)]
5width=0.3
6
7pylab.bar(np.arange(len(true_data)),true_data,width=width,label='True')
8pylab.bar(np.arange(len(true_data))+width,unif_data,width=width,label='Uniform')
9pylab.xlabel('Different Teeth Bins',fontsize=18)
10pylab.title('Probability Distribution of Space Worm Teeth',fontsize=18)
11pylab.ylabel('Probability',fontsize=18)
12pylab.xticks(np.arange(len(true_data)))
13pylab.legend()
14pylab.show()به نظر میرسد که شباهت زیادی بین توزیع واقعی دادههای و توزیع یکنواخت (Uniform) وجود ندارد. در این صورت بهتر است از توزیع دیگری در این زمینه مثلا «توزیع دوجملهای» (Binomial) استفاده کنیم.
توزیع دوجملهای نیز یکی از توزیعهای آماری است که مقدارهای گسسته (شمارشی) را شامل میشود بنابراین شرط اولیه که مطابقت تکیهگاه (مجموعه مقدارها) توزیع با مقدارهای متغیر مشاهده شده است را دارد. تابع احتمال متغیر تصادفی با توزیع دوجملهای به صورت زیر نوشته میشود.
$$\large P(X=x)={ n \choose x}p^x(1-p)^{n-x}$$
مشخص است که در اینجا $$x$$ تعداد موفقیتها در n بار تکرار آزمایش برنولی است. میدانیم که میانگین (امیدریاضی) و واریانس متغیر تصادفی دوجملهای به ترتیب برابر با $$np$$ و $$np(1-p)$$ است.
با توجه به مفهوم امیدریاضی برای توزیع دوجملهای و همچنین میانگین وزنی برای دادهها، محاسبات را انجام داده و نتایج را مقایسه میکنیم. مطابق با جدول فراوانی میانگین وزنی به صورت زیر محاسبه میشود.
$$weighted\;mean=0\times 0.02+1\times 0.03+2\times 0.05+\cdots+10\times 0.07=5.44$$
به این ترتیب میتوانیم مقدار احتمال موفقیت ($$p$$) را محاسبه کنیم.
$$\large p=\dfrac{weighted\;mean}{n}=\dfrac{5.44}{10}=0.544$$
شاید به نظر برسد که مقدار $$n$$ باید برابر با ۱۱ (تعداد پشامدها) یا ۱۰۰ (تعداد کرمها) باشد. دلیل اینکه مقدار $$n=10$$ انتخاب شده است را در ادامه خواهید دید.
میدانیم که توزیع دوجملهای، از جمع n متغیر تصادفی برنولی که هر کدام مقدار 0 و 1 میگیرند، ساخته میشود. بنابراین اگر برای مثال یک سکه را ۱۰ بار پرتاب کنیم، احتمال مشاهده $$x$$ شیر (موفقیت) از طریق توزیع دوجملهای میسر است. مشخص است که تعداد موفقیتها در این بین شامل مقدارهای 0 تا ۱۰ است. بنابراین، همین فرضیات را برای تعداد دندانهای کرمها نیز خواهیم داشت.
به این ترتیب در مثال ما، تعداد دندانهای هر کرم میتواند از ۰ تا ۱۰ دندان تغییر کند و میتوانیم مشاهده دندان (وجود یا ناموجود) را به صورت ۰ و ۱ مشخص کنیم. از آنجایی که حداکثر تعداد دندانها برابر با ۱۰ است، تعداد موفقیتها (تعداد ۱ها) حداکثر برابر با ۱۰ خواهد بود. در نتیجه باید مقدار $$n=10$$ در نظر گرفته شود. حال به محاسبه احتمال مطابق توزیع دوجملهای با پارامتر $$p=0.544$$ و $$n=10$$ خواهیم پرداخت. در این حالت میگوییم تعداد دندانهای کرمهای فضایی دارای توزیع دوجملهای با پارامترهای $$p$$ و $$n$$ است و این جمله را با نماد ریاضی به صورت $$X\sim B(n,p)$$ نشان میدهیم.
$$\large P(X=0)={10 \choose 0} 0.544^0 (1-0.544)^{10}=0.0004$$
$$\large P(X=۱)={10 \choose 1} 0.544^1 (1-0.544)^{9}=0.0046$$
$$\large P(X=۲)={10 \choose ۲} 0.544^۲ (1-0.544)^{۸}=0.0249$$
...
$$\large P(X=۹)={10 \choose ۹} 0.544^۹ (1-0.544)^{۱}=0.0190$$
$$\large P(X=10)={10 \choose 10} 0.544^{10} (1-0.544)^{0}=0.0023$$
احتمالات حاصل را مطابق با نمودار زیر با احتمالات مربوط به دادههای واقعی (ستون درصد فراوانی) در جدول فراوانی مقایسه میکنیم. کدی که در ادامه قابل مشاهده است برای ترسیم چنین نموداری به کار رفته است.
1def get_bino_probability(mean,k,n):
2 return (factorial(n)/(factorial(k)*factorial(n-k)))*(mean**k)*((1.0-mean)**(n-k))
3
4def get_bino_success(true_data,n):
5 return np.sum(np.array(true_data)*np.arange(len(true_data)))/10.0
6
7n_trials = 10
8succ = get_bino_success(true_data,n_trials)
9print('Success probability: ',succ)
10
11bino_data = [get_bino_probability(succ,k,n_trials) for k in range(11)]
12
13width=0.3
14
15pylab.bar(np.arange(len(true_data)),true_data,width=width,label='True')
16pylab.bar(np.arange(len(true_data))+width,bino_data,width=width,label='Binomial')
17pylab.xlabel('Different Teeth Bins',fontsize=18)
18pylab.title('Probability Distribution of Space Worm Teeth',fontsize=18)
19pylab.ylabel('Probability',fontsize=18)
20pylab.xticks(np.arange(len(true_data)))
21pylab.legend()
22pylab.show()مقدار احتمال موفقیت در این حالت در ادامه دیده میشود.
1Success probability: 0.5439999999999999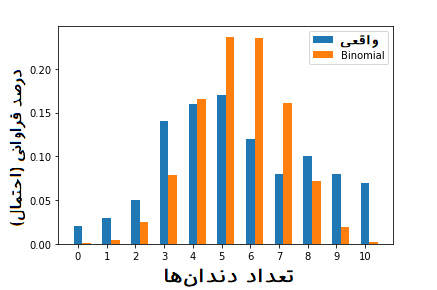
اینطور که به نظر میرسد، بین احتمالات واقعی و تابع احتمال دوجملهای، مطابقت خوبی برقرار است. به نظر میرسد مشخص کردن توزیع احتمالی دندانهای کرمهای فضایی با موفقیت همراه بوده است. بنابراین کافی است که توزیع دوجملهای با پارامترهای آن را برای زمین مخابره کنیم تا اطلاعات کافی در مورد دندانهای کرمهای فضایی را به ایستگاه زمینی داده باشیم.
البته شاید بد نباشد که مقایسه سه تایی (توزیع یکنواخت، دوجملهای و توزیع واقعی) توزیعها را نیز رسم کنیم و در بایگانی فضاپیما نگهداری کنیم.
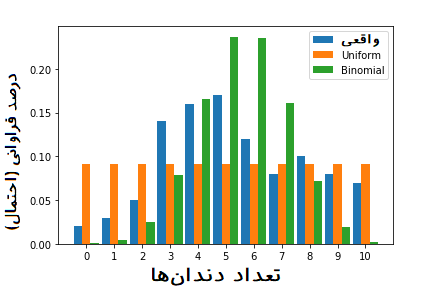
کدهای زیر برای ترسیم چنین نموداری در پایتون استفاده شده است.
1pylab.bar(np.arange(len(true_data))-width,true_data,width=width,label='True')
2pylab.bar(np.arange(len(true_data)),unif_data,width=width,label='Uniform')
3pylab.bar(np.arange(len(true_data))+width,bino_data,width=width,label='Binomial')
4pylab.xlabel('Different Teeth Bins',fontsize=18)
5pylab.title('Probability Distribution of Space Worm Teeth',fontsize=18)
6pylab.ylabel('Probability',fontsize=18)
7pylab.xticks(np.arange(len(true_data)))
8pylab.legend()
9pylab.show()معیار واگرایی کولبک-لبیلر (KL) برای تشخیص توزیع مناسب
مطابق با نمودارهای ترسیم شده شاید بتوان نتیجه گرفت که توزیع دوجملهای مناسبتر از توزیع یکنواخت است. ولی در اینجا قصد داریم به کمک یک شاخص میزان این مطابقت را اندازهگیری کنیم.
معیار واگرایی کولبک-لیبلر برای مقایسه توزیعهای گسسته $$p$$ با $$q$$ به صورت زیر تعریف میشود.
$$\large D_{KL}(p||q)=\sum_{i=1}^Np(x_i)\log(\frac{p(x_i)}{q(x_i)})$$
در این تعریف فرض شده است که $$p(x)$$ توزیع واقعی و $$q(x)$$ توزیع تقریبی برای دادهها است. این شاخص نشان میدهد که توزیع تقریبی چقدر نسبت به توزیع واقعی دور است.
اگر توزیعهای از نوع پیوسته باشند تعریف معیار KL برحسب انتگرال خواهد بود. به رابطه زیر توجه کنید.
$$\large D_{KL}(p||q)=\int_{-\infty}^{\infty} p(x_i)\log(\frac{p(x_i)}{q(x_i)})dx$$
همانطور که دیده میشود، یکی از اجزای محاسباتی برای شاخص KL، لگاریتم نسبت دو توزیع است. هر چه مقدار $$q(x_i)$$ بزرگتر از $$p(x_i)$$ باشد به معنی محتملتر بودن مقدار $$x_i$$ در توزیع $$q$$ است. پس کسر $$\frac{p(x_i)}{q(x_i)}$$ کوچکتر از ۱ میشود. بنابراین لگاریتم این کسر منفی خواهد شد. از طرفی اگر $$q(x_i)$$ کوچکتر از $$p(x_i)$$ باشد، نسبت این دو بزرگتر از ۱ شده و لگاریتم آن نیز مثبت است. در صورتی که این نسبت برابر با ۱ باشد (یعنی دو توزیع یکسان باشند)، مقدار لگاریتم، صفر خواهد شد.
به نظر میرسد شاخص KL، امید ریاضی (مقدار مورد انتظار) برحسب توزیع $$p$$ لگاریتم نسبت دو توزیع باشد. بنابراین ناحیه مطابقت دو توزیع زمانی که $$p(x_i)$$ بزرگتر است اهمیت (وزن) بیشتری در محاسبه KL نسبت به ناحیهای دارد که $$p(x_i)$$ کوچکتر است. به این ترتیب در نواحی که دو توزیع دارای تکیهگاه یکسانی نیستند، اهمیت یا مقدار احتمالات کاهش مییابد.
برای این شاخص میتوان خصوصیات زیر را نتیجه گرفت.
- شاخص KL همیشه نامنفی است.
- شاخص KL متقارن نیست. به این معنی که $$D_{KL}(p||q)\neq D_{KL}(q||p)$$
- شاخص KL برای مقایسه هر توزیع با خودش برابر با صفر است. در نتیجه بیشترین مطابقت توسط این شاخص با صفر مشخص میشود.
- شاخص KL برای متغیرهای تصادفی مستقل به صورت جمع نوشته میشود. این امر درست به مانند بینظمی شانون است. در نتیجه اگر $$p(x,y)=p_1(x)p_2(y)$$ باشد، آنگاه:
$$\large D_{KL}(p||q)=D_{KL}(p_1||q)+D_{KL}(p_2||q)$$
حال به بررسی مثال کرمهای فضایی و محاسبه شاخص KL برای هر دو توزیع یکنواخت و دوجملهای خواهیم پرداخت. با توجه به رابطه KL برای متغیرهای تصادفی گسسته، شاخص KL برای توزیع یکنواخت به صورت زیر محاسبه میشود.
$$\large D_{KL}(True||Unifrm)=0.02\log(\frac{0.02}{0.0909})+0.03\log(\frac{0.03}{0.0909})+\\ \large \cdots+0.08\log(\frac{0.08}{0.0909})+0.07\log(\frac{0.07}{0.0909})=0.136$$
همین محاسبات را نیز برای مطابقت توزیع دوجملهای با توزیع واقعی دادهها انجام میٔهیم.
$$\large D_{KL}(True||Binomial)=0.02log(\frac{0.02}{0.0004})+0.03\log(\frac{0.03}{0.0046})+\\ \large \cdots+0.08\log(\frac{0.08}{0.0190})+0.07\log{(0.07}{0.0023})=0.427$$
برای محاسبه شاخص KL از قطعه کد زیر نیز میتوانید استفاده کنید.
1def get_klpq_div(p_probs, q_probs):
2 kl_div = 0.0
3
4 for pi, qi in zip(p_probs, q_probs):
5 kl_div += pi*np.log(pi/qi)
6
7 return kl_div
8
9def get_klqp_div(p_probs, q_probs):
10 kl_div = 0.0
11
12 for pi, qi in zip(p_probs, q_probs):
13 kl_div += qi*np.log(qi/pi)
14
15 return kl_div
16
17print('KL(True||Uniform): ',get_klpq_div(true_data,unif_data))
18print('KL(True||Binomial): ',get_klpq_div(true_data,bino_data))نتیجه اجرای این برنامه به صورت زیر است.
1KL(True||Uniform): 0.13667971094966938
2KL(True||Binomial): 0.42734972485619327هر چه مقدار شاخص KL کوچکتر باشد، میزان مطابقت بین توزیع $$p(x)$$ با $$q(x)$$ بیشتر است. با کمال تعجب میبینیم که مقدار شاخص KL برای توزیع یکنواخت کوچکتر از توزیع دوجملهای است. بنابراین توزیع یکنواخت بهتر میتوان دادههای مربوط به تعداد دندانهای کرمهای فضایی را بیان کند. این امر نشان میدهد که همیشه نمیتوان به شهود و نتایج حاصل از آن اعتماد کرد. یا حداقل شاخص KL نظر ما را در این امر تایید نمیکند.
بهتر است برای تشخیص اینکه مقدار احتمال موفقیت در توزیع دوجملهای چه تاثیری در شاخص KL دارد، از نموداری استفاده کنیم که به ازاء مقدارهای مختلف $$p$$ در توزیع دوجملهای، شاخص KL را مقایسه کند. کدهای مربوط به ترسیم چنین نموداری در ادامه قابل مشاهده است.
1n_trials = 10
2succ = get_bino_success(true_data,n_trials)
3
4x = np.arange(0.02,1.0,0.02)
5
6kl_divs = []
7for xi in x:
8 bino_data = [get_bino_probability(xi, k, n_trials) for k in range(11)]
9 kl_divs.append(get_klpq_div(true_data, bino_data))
10
11print('KL divergence at mean-delta: ', get_klpq_div(true_data,[get_bino_probability(succ-0.001, k, n_trials) for k in range(11)]))
12print('KL divergence at mean: ', get_klpq_div(true_data,[get_bino_probability(succ, k, n_trials) for k in range(11)]))
13print('KL divergence at mean+delta: ', get_klpq_div(true_data,[get_bino_probability(succ+0.001, k, n_trials) for k in range(11)]))
14pylab.plot(x,kl_divs)
15# we plot our choice for the binomial success probability on the same curve
16pylab.scatter(succ,get_klpq_div(true_data,[get_bino_probability(succ, k, n_trials) for k in range(11)]),color='r')
17pylab.xlabel('Binomial Success Probability')
18pylab.ylabel('KL(P||Q) divergence')
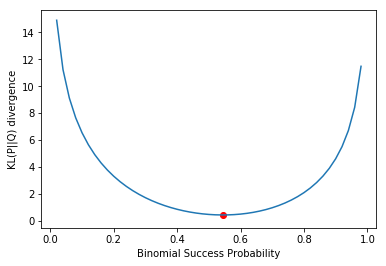
19pylab.show()نتیجه اجرای این کد، نموداری است که تقریبا نشان میدهد، کمترین مقدار KL برای مقایسه توزیع واقعی و دوجملهای در همان مقدار احتمال 0.544 (که با نقطه قرمز رنگ مشخص شده) بدست میآید. بنابراین باز هم شاخص KL گواهی میدهد که توزیع یکنواخت میتواند اطلاعات بیشتری در مورد توزیع واقعی دادهها در اختیارمان قرار دهد.
اگر مطلب بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- مجموعه آموزشهای یادگیری ماشین و بازشناسی الگو
- آموزش آمار و احتمال مهندسی
- آموزش یادگیری ماشین
- آموزش یادگیری ماشین (Machine Learning) با پایتون (Python)
- احتمال شرطی (Conditional Probability) — اصول و شیوه محاسبه
- قضیه بیز در احتمال شرطی و کاربردهای آن
- تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده
^^











سلام
ممنون از توضیحات
من با فاصله جنسون شانون کار میکنم میخواستم ببینم ممکن است که این فاصله در داده های واقعی منفی شود؟
بسیار عالی
خیلی ممنون بابت توضیح خوبتون
بسیار عالی بود، تمام مطالبی که از آقای دکتر ری بد مطالعه کردم خیلی شفاف و رسا توضیح داده شده است.
سپاس
بسیار عالی و مفید. تشکر